-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Electrical and Electronic Engineering
p-ISSN: 2162-9455 e-ISSN: 2162-8459
2012; 2(4): 230-235
doi: 10.5923/j.eee.20120204.09
Multiobjective Optimization of an Operational Amplifier by the Ant Colony Optimisation Algorithm
Benhala Bachir , Ahaitouf Ali , Mechaqrane Abdellah
Sidi Mohamed Ben Abdellah University, Faculty of Science and Technology, Laboratory of Signals, Systems and Component
Correspondence to: Benhala Bachir , Sidi Mohamed Ben Abdellah University, Faculty of Science and Technology, Laboratory of Signals, Systems and Component.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The Ant Colony Optimization (ACO) algorithm is used as a multi-objective optimization technique to size a most popular analog circuit, the CMOS operational amplifier (Op-Amp). The work consist of finding the more convenient transistors sizes, including the channel widths and lengths, in order to meet or reach the specified requirements such as the voltage gain Av, the Common Mode Rejection Ratio CMRR, the die area A, the power consumption P and the Slew Rate SR. SPICE simulations are used to strengthen and to validate the obtained sizing/performances.
Keywords: Ant Colony Optimization, Multi-objective optimization, CMOS, Op-Amp
Article Outline
1. Introduction
- Over the past decade, significant progress has been realized with the appearance of a new generation of powerful and approximate optimization methods, known as metaheuristics[1]. Such methods are used to solve real-world problems within a reasonable amount of time. They always offer ‘good’ approximation of the ‘best’ solutions for optimization problems[2]. One of the incoming problems to be resolved in the nearer future is the sizing of electronic circuits given the continuous increase of the integration densities. So, the designers and electronic engineers had a good and exciting challenge to reach, that is to find a technique, which can easily determine the components sizing, taken into account a well determined specifications. Some (meta-) heuristics were proposed in the literature and were used by some designers to optimize the sizing of the analog components automatically, such as Tabu Search[3,4], Genetic Algorithms (GA)[5], local search (LS)[6], Wasp Nets (WN)[7], Bacterial Foraging Optimization (BFO)[8], Particle Swarm Optimization (PSO)[9] and recently Ant Colony Optimization(ACO)[10,11].These algorithms have often dealt with single-objective optimizations; however, the optimization of analog circuits is generally a multi-objective problem. They are always formed by at least two conflicting performance functions.That means that improving one performance results automatically into the degradation of another one. In this way a set of several meta-heuristics algorithms have been developed, such as Multi-objective Optimization Genetic Algorithm (MOGA)[12], Multi-objective Optimization Particle Swarm Optimization (MOPSO)[13].In the domain of meta-heuristic methods, an important interest has been paid to the Ant Colony Optimization algorithm. The basic idea is to imitate the cooperative behaviour of ant colonies in order to solve combinatorial optimization problems within a reasonable amount of time, The ACO is actually recognized as one of the most successful strands of swarm intelligence[14]. Some ACO-based algorithms have been proposed such as the multi-objective optimization problems MOACO[15], the Multiple Objective Ant-Q Algorithm (MOAQ)[16], the Pareto-Ant Colony Optimization (P-ACO)[17] and the Ant Algorithm for Bi-criterion Optimization Problems[18].In a previous work, we have adapted and used the MOACO algorithm for a two objectives electronic circuit optimization namely the Second Generation Current Conveyors[19]. At the present we propose to use the same algorithm in order to optimize the sizing of the CMOS Op-Amp, which is a more popular analog circuit requiring many highly interdependent performances.Thus the subsequent section will present an overview of the ACO technique followed by with a presentation of the proposed adaptation of the ACO technique for analog circuits optimization and introduces the MOACO. The third deals with the optimal sizing of the CMOS Operational Amplifier (Op-Amp) and presents the main results and simulations. Finally, the paper will be concluded in the final section.
2. Algorithm Presentation
2.1. Ant Colony Optimization
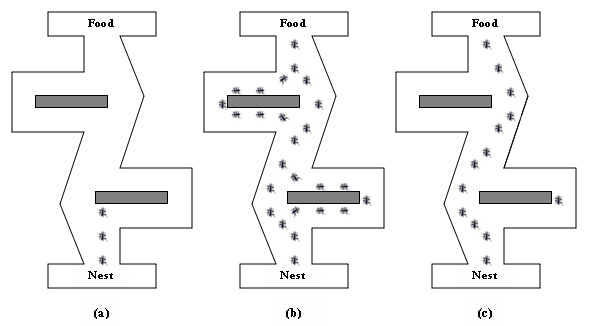
- The ACO technique is inspired by the collective behavior of deposition and monitoring of some traces as it is observed in insect colonies [20,21], such as ants. It is for example well known that ants deposit pheromone on the ground in order to mark some favourable paths that should be followed by other members of the colony. Fig. 1 shows an illustration of the ability of ants to find the shortest path between food and their nest. Ants communicate indirectly through dynamic changes in their environment (pheromone trails).
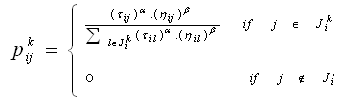 | (1) |
 is the set of neighbours of the vertex i of the kth ant,
is the set of neighbours of the vertex i of the kth ant,  is the amount of pheromone trail on the edge (i, j), α and β are weightings that control the pheromone trail
is the amount of pheromone trail on the edge (i, j), α and β are weightings that control the pheromone trail 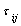 and the visibility value,
and the visibility value, 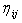 given by:
given by: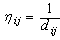 | (2) |
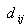 is the distance between vertices i and j.The pheromone rate values are updated during each iteration by all the m ants that have built a solution in the iteration itself. The pheromone rate
is the distance between vertices i and j.The pheromone rate values are updated during each iteration by all the m ants that have built a solution in the iteration itself. The pheromone rate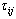 , which is associated with the edge joining vertices i and j, is updated as follows:
, which is associated with the edge joining vertices i and j, is updated as follows: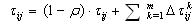 | (3) |
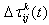 is the quantity of pheromone laid ‘deposited, or dropped of’on edge (i, j) by ant k:
is the quantity of pheromone laid ‘deposited, or dropped of’on edge (i, j) by ant k: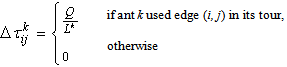 | (4) |
2.2. Adaptation
- The main idea consists of constructing a graph that imitates the movement of the ants[28,29]. Then, we construct a graph composed of the discretized variable vectors, corresponding to the graph vertices. Thus, each ant will construct its path by a random displacement from a variable value to another, as it is shown in Fig. 2; V1, V2, V3…VN constitute the discrete variable vectors.
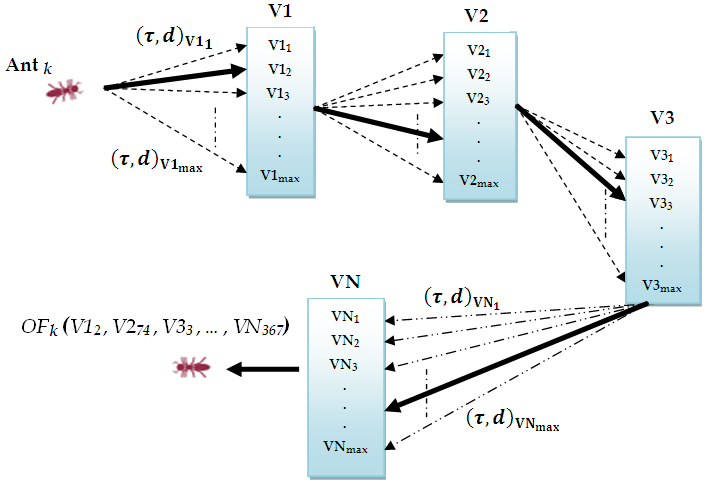 | Figure 2. A pictorial graph showing the movement of the ants |
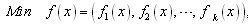 with
with 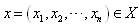 .A decision vector
.A decision vector  dominates another
dominates another 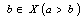 if, and only if:
if, and only if: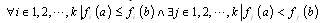
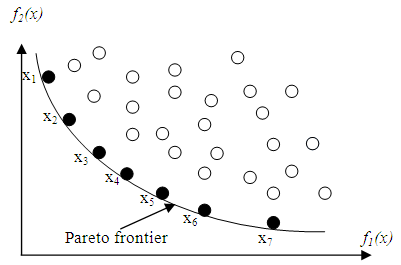 | Figure 3. Non-dominated solutions for two-objective optimization problem |
 | Figure 4. Pseudo code for the proposed MOACO algorithm |
3. Operational Amplifier Optimization
- The two-stage CMOS operational amplifier (Op-Amp) shown in Figure 5, is considered as an example for the validation of our proposed algorithm. In fact the design of the Op-Amp continues to pose a challenge as transistor channel lengths scale down with each generation of CMOS technologies[32].
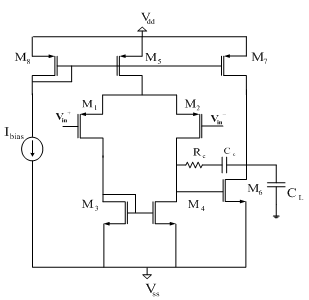 | Figure 5. A two stage CMOS operational amplifier |
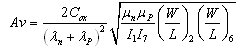 | (5) |
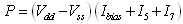 | (6) |
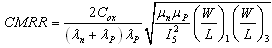 | (7) |
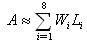 | (8) |
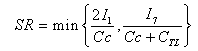 | (9) |
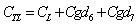 | (10) |
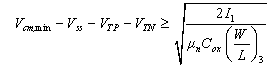 | (11) |
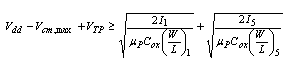 | (12) |
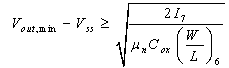 | (13) |
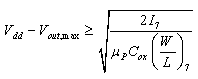 | (14) |
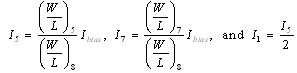 while respecting the expression (15):
while respecting the expression (15):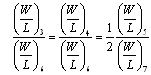 | (15) |
|
|
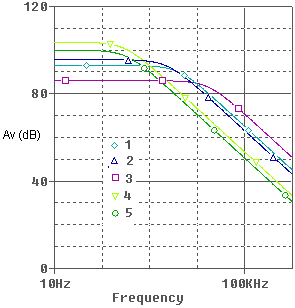 | Figure 6. Spice simulation results for Gain |
4. Conclusions
- The presented work proposes an adaptation of the ant colony optimization technique to the optimal sizing of analog circuits. We show the practical applicability of the ACO to optimize performances of electronics integrated circuits and its suitability for solving a multiobjective optimization problem. The proposed algorithm is validated by the Operational Amplifier performances optimization. Viability of the technique was proved via SPICE simulations.
References
| [1] | C.R. Reeves, “Modern heuristic techniques for combinatorial problems,” Blackwell Scientific Publications, Oxford, 1993. |
| [2] | I.H. Osman, J.P. Kelly, “Meta-heuristics: theory and applications,” Kluwers Academic Publishers, Boston, 1996. |
| [3] | F. Glover, “Tabu search-part I,” ORSA Journal on computing, Vol. 1, No 3, 1989, pp. 190–206. |
| [4] | F. Glover, “Tabu search-part II,” ORSA Journal on computing, Vol. 2, No 1, 1990, pp. 4–32. |
| [5] | J. B. Grimbleby, “Automatic analogue circuit synthesis using genetic algorithms,” IEE Proceedings-Circuits, Devices and Systems, Vol. 147, No 6, 2000, pp. 319–323. |
| [6] | E. Aarts, K. Lenstra, “Local search in combinatorial optimization,” Princeton: Princeton University Press, 2003. |
| [7] | F. T. S. Chan, M. K. Tiwari, “Swarm Intelligence: focus on ant and particle swarm optimization,” I-Tech Education and Publishing, 2007. |
| [8] | A. Chatterjee, M. Fakhfakh, P. Siarry, ‘‘Design of Second Generation Current Conveyors Employing Bacterial Foraging Optimization,” Microelectronics Journal, Elsevier, vol. 41, 2010, pp. 616–626. |
| [9] | M. Fakhfakh, Y. Cooren, A. Sallem, M. Loulou, P. Siarry “Analog Circuit Design Optimization through the Particle Swarm Optimization Technique,” Journal of Analog Integrated Circuits & Signal Processing, Springer, Vol. 63, No 1, April, 2010, pp. 71–82. |
| [10] | B. Benhala, A. Ahaitouf, A. Mechaqrane, B. Benlahbib, F. Abdi, E. Abarkan, M. Fakhfakh “Sizing of current conveyors by means of an ant colony optimization technique,” Proceedings of the 2nd International Conference on Multimedia Computing and Systems (ICMCS'11), IEEE Press, 2011, pp. 899–904. |
| [11] | B. Benhala, A. Ahaitouf, M. Kotti, M. Fakhfakh, B. Benlahbib, A. Mecheqrane, M. Loulou, F. Abdi, E. Abarkane “Application of the ACO Technique to the Optimization of Analog Circuit Performances,” a chapter in Analog Circuits: Applications, Design and Performance, (Ed.) T. Cuautle, NOVA Science Publishers, Inc. ISBN: 978-1-61324-355-8, 2011, pp. 235–255. |
| [12] | A. sallem, M. Fakhfakh, M. Loulouo “ptimizing CMOS Current Conveyor through MOGA and High Frequency Applications,” SETIT 2009 5th International Conference: Sciences of Electronic, Technologies of Information and Telecommunications, TUNISIA, 2009. |
| [13] | M. Fakhfakh, Y. Cooren, A. Sallem, M. Loulou, P, Siarry “Analog circuit design optimization through the particle swarm optimization technique,” Journal Analog Integrated Circuits and Signal Processing, Vol. 63 No 1, April 2010. |
| [14] | E. Bonabeau, M. Dorigo, G. Theraulaz, “Inspiration for optimization from social insect behavior,” Nature 2000, Vol. 406, pp. 39–42. |
| [15] | C. Garcia-Martinez, O. Cordon, F. Herrera, “A Taxonomy and an Empirical Analysis of Multiple Objective Ant Colony Optimization Algorithms for the Bi-criteria TSP,” European Journal of Operational Research, Vol. 180, No 1, July 2007, pp. 116–148. |
| [16] | C. E. Mariano, E. Morales, “A Multiple Objective Ant-Q Algorithm for the Design of Water Distribution Irrigation Networks,” Technical Report HC-9904, Instituto Mexicano de Tecnologia del Agua, Mexico, June, 1999. |
| [17] | K. Doerner, W. J. Gutjahr, R. F. Hartl, C. Strauss and C. Stummer, “Pareto Ant Colony Optimization: A Metaheuristic Approach to Multiobjective Portfolio Selection,” Annals of Operations Research, 2004. |
| [18] | S. Iredi, D. Merkle, M. Middendorf, “Bi-Criterion Optimization with Multi Colony Ant Algorithms,” Proc. First International Conference on Evolutionary Multi-criterion Optimization (EMO'01), Lecture Notes in Computer Science 2001, pp. 359–372. |
| [19] | B. Benhala, A. Ahaitouf, A. Mechaqrane, B. Benlahbib, “Multiobjective Optimization of Second Generation Current Conveyors by the ACO Technique”, Proceedings of the 3nd International Conference on Multimedia Computing and Systems (ICMCS'12), May 10-12 2012, Tangier, Morocco, IEEE Press. |
| [20] | S. D. Shtovba, “Ant Algorithms: Theory and Applications,” Programming and Computer Software, Vol. 31, No 4, 2005, pp. 167–178. |
| [21] | J. Dreo, A. Pétrowski, P. Siarry, E. Taillard, “Metaheuristics for hard optimization: Methods and case studies,” New York: Springer, 2006. |
| [22] | Y. Jinhui, S. Xiaohu , M. Maurizio, L. Yanchun, “An ant colony optimization method for generalized TSP problem,” Progress in Natural Science, Vol. 18, No 11, November 2008, pp. 1417–1422. |
| [23] | B. Yu, Z. Yang, B. Yao, “An improved ant colony optimization for vehicle routing problem,” European Journal of Operational Research 196, 2009, pp. 171–176. |
| [24] | G.N. Varela, M.C. Sinclair, “Ant colony optimisation for virtual-wavelength-path routing and wavelength allocation,” Evolutionary Computation, CEC Proceedings Congress on Washington, DC, USA, 1999. |
| [25] | A. Shmygelska, H. Hoos, “An ant colony optimisation algorithm for the 2D and 3D hydrophobic polar protein folding problem,” BMC Bioinformatics; Vol. 6 No 30, 2005, pp. 1–22 |
| [26] | M. Dorigo, G. DiCaro, L. M. Gambardella, “Ant algorithms for discrete optimization,” Artificial Life Journal, vol. 5, 1999, pp. 137-172. |
| [27] | M. Dorigo, T. Stüzle, “Ant Colony Optimization, “ MIT Press, 2004. |
| [28] | S. D. Shtovba, “Ant Algorithms: Theory and Applications,” Programming and Computer Software, vol. 31, No. 4, 2005, pp. 167–178. |
| [29] | E. Salari, K. Eshghi, “An ACO algorithm for graph coloring problem,” Computational Intelligence Methods and Applications, 2005. |
| [30] | M. Basseur, E.G. Talbi, A. Nebro, E. Alba, “Metaheuristics for multiobjective combinatorial optimization problems,” Review and recent issues, report no 5978. National Institute of Research in Informatics and Control (INRIA). September 2006. |
| [31] | R. H. Dinger, “Engineering design optimization with genetic algorithm,” The IEEE Northcon Conference. October 21–23, 1998, Seattle WA, USA 1998. |
| [32] | B. Razavi, “Design of Analog CMOS Integrated Circuits,“ McGraw-Hill International Edition: Electrical Engineering Series, 2002. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML