H. Shayeghi , J. Dadashpour
Technical Engineering Department, University of Mohaghegh Ardabili, Ardabil, Iran
Correspondence to: H. Shayeghi , Technical Engineering Department, University of Mohaghegh Ardabili, Ardabil, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper addresses a robust method for optimal PID control of Automatic Voltage Regulation (AVR) system to damp terminal voltage oscillation following disturbances in power systems. The optimization is carried out by the Anarchic Society Optimization (ASO) algorithm which is inspired by a social grouping in which members behave anarchically to improve their situation. The optimal tuning problem of the PID gains to control of AVR system against parametric uncertainties is formulated as an optimization problem according to time domain based objective function. It is solved by the ASO algorithm which has a strong ability to find the most optimistic results to reduce control system effort and find optimal design. It is carried out under multiple operation conditions to achieve the desired level of terminal voltage regulation. The effectiveness of the optimized PID controller with ACO algorithm is investigated under system parameter changes in comparison with the results of PID controller tuned via of the recently reported optimization method like the craziness based Particle Swarm Optimization (PSO) and Vector Evaluated PSO (VEPSO) approaches. The simulation results is depicted to illustrate robust performance of the proposed ASO technique for enhancement transient stability of AVR system that of the other heuristics methods in the literature. The results analysis reveals that the ASO based PID type AVR control system is effective and provides good terminal voltage oscillations damping ability. Moreover, it is superior that of the other PSO method in terms of accuracy, convergence and computational effort.
Keywords:
AVR, ASO Algorithm, PID Controller, Power System Dynamics
1. Introduction
In resent years, the scale of power systems has been expanded, and with that stability and constancy of nominal voltage level in an electric power grid is becoming more important. One of method for increasing stability and achieving nominal voltage level in an electric power grid is raising the voltage or employing series capacitors in power transmission lines, but controlling of generator exciter by using of Automatic Voltage Regulator (AVR) is attracting attention because of its inherent cost advantage[1]. The generator excitation system maintains generator voltage and controls the reactive power flow using an automatic voltage regulator[4]. The task of an AVR system is to hold the terminal voltage magnitude of a synchronous generator at a specified level. Thus, the stability of the AVR system would seriously affect the security of the power system. Despite the potential of the modern control techniques with different structure, Proportional Integral Derivative (PID) type controller is still widely used for AVR system [1-2]. This is because it performs well for a wide class of process. Also, they give robust performance for a wide range of operating conditions and easy to implement. On the other hand, Mukherjee and Ghoshal[3] have presented a comprehensive analysis of the effects of the different PID controller parameters on the overall dynamic performance of the AVR system. It is shown that the appropriate selection of PID controller parameters results in satisfactory performance during system upsets. Thus, the optimal tuning of a PID gains is required to get the desired level of robust performance. Since optimal setting of PID controller gains is a multimodal optimization problem (i.e., there exists more than one local optimum) and more complex due to nonlinearity, complexity and time-variability of the real world power systems operation. Hence, local optimization techniques, which are well elaborated upon, are not suitable for such a problem. Recently, global optimization techniques like genetic algorithm, bacterial foraging, Particle Swarm Optimization (PSO), Craziness based PSO (CRPSO), Vector Evaluated PSO (VEPSO) and artificial bee colony (ABC)[3-7] have been applied for optimal tuning of PID controller of an AVR system. In [3] for tuning of PID controller gains with off-line, as well as, nominal input conditions, was represented a CRPSO based search technique. For on-line input conditions, Sugeno Fuzzy Logic (SFL) has been used. It was shown that better quality solution of step response of terminal voltage with less computational effort has been obtained in CRPSO-SFL based PID controller than the binary coded genetic algorithm SFL based PID controller one. Giang [4] proposed a PSO based PID type controller for AVR system using the optimization of a time domain performance criterion. This performance index includes some system characteristics such as overshoot, steady state error, deviation between settling time and rise time. It has better quality solution than the GA based tuned PID controller. However, the performance of the proposed PSO algorithm is dependent to suitable selection of PSO control parameters. Kim and Cho [5] developed an optimal tuning method using hybrid Genetic Algorithm (GA) and Bacterial Foraging (BF) technique in order to improve the performance PID control of AVR system. Gozde and colleagues [6] suggested the ABC based self tuning PID controller for AVR system and compared the results with that of PSO based methods. The simulated results show that it has better performance than the PSO algorithm one. In [7] a VEPSO based self tuning PID controller for AVR system is represented in comparison with the CRPSO based method.It should be noted these evolutionary algorithms are heuristic population-based search procedures that incorporate random variation and selection operators. Although, they seem to be good approaches for the solution of PID gains optimization problem, However, when the system has a highly epistatic objective function (i.e. where parameters being optimized are highly correlated), and number of parameters to be optimized is large, then they have degraded efficiency to obtain global optimum solution. In order to overcome these drawbacks, the Anarchic Society Optimization (ASO) algorithm is proposed to find optimal gains of PID controller for AVR system. It is a new heuristic method which is inspired by a social grouping in which members behave anarchically to improve their situation. The foundation of ASO is a group of individuals who are fickle, adventurous, dislike stability, and frequently behave irrationally, moving toward inferior positions they have visited during the exploration phase. The level of anarchic behaviour among members intensifies as the level of difference among members’ situations enhances. Using these anarchic members, ASO explores the solution space completely and avoids falling into local optimum solutions. The main feature of ASO is that it converges in the limit to a globally optimal solution with probability one under mild conditions. Also, it is more general and can easily be used for both continuous and discrete problems unlike PSO which were firstly commenced for continuous and discrete optimization, respectively. This feature is caused that the ASO algorithm has been had a flexible and well-balanced mechanism to enhance the global and local exploration abilities and found to be robust in solving multi objective problems featuring non-linearity, non- differentiability and high dimensionality. In this study, the problem of robustly PID gains tuning is formulated as an optimization problem based on time domain based objective function. The optimization is carried out under multiple operation points by ASO algorithm such that the relative stability is guaranteed and the time domain specifications concurrently secured. The effectiveness of the ASO based optimized PID controller is demonstrated in comparison with the designed controller using CRPSO and VEPSO methods through time domain simulation studies and some performance indices to greatly damp terminal voltage oscillations under different plant parameter changes. Results evaluation show that the proposed method is effective and alternative to PID fixed gain controller design as it retains the simplicity of the controller and still guarantees a robust acceptable performance over a wide range of operating and system conditions.
2. ASO Algorithm
Natural evolution based heuristic optimization methods like genetic algorithms, evolutionary programming, differential evolutionary and swarm-intelligence based random optimization algorithms such as Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO) have been widely used to solve difficult combinatorial optimization problems more than three decades. These methods are based on simulating natural, social insect colonies and animal group behaviour to infer fundamentals of self-organization and cooperation. Note that the structure of a nature-inspired swarm intelligence method strongly depends on the personal and social characteristics of its population’s members. Thus, choosing an appropriate underlying society is very important for developing such algorithms. Anarchic Society Optimization (ASO) developed by Ahmadi-Javid[8] is a first introduced human-inspired swarm intelligence optimization method. This novel random method is based on an abnormal human society instead of a swarm of birds or a colony of ants, which are the basis of PSO and ACO, respectively. It should be noted that humankind has very special and unique characteristics than social insect colonies and animal groups.ASO is a modern optimization method inspired by a human society whose entities behave anarchically to enhance their situations. In ASO algorithm the entities are fickle and their irregularity increases as their situation worsens. They also behave illogically and bravely, moving toward the inferior positions they have visited. Using these chaotic members, ASO is able to search the solution space perfectly and avoid falling into local optimum solutions.
2.1. Basic assumptions and notation
Assume that S be a solution space and f(.) be a cost function needs to be minimized over S. Consider a society of N members searching within an unknown land, i.e. the solution space, for the best place to live, i.e. the global minimizer of f over S. The main feature of the society is that its members are brave and behave anarchically during their search process.Consider Xi(k) is the position of member i in iteration k of the exploring procedure. All of the members are aware of the best global position (G(k)) which is called G-best visited by the whole society in the first k iterations. They also realize member i*k who occupies the best position in the society in iteration k. The best personal position (P-best) previously visited by member i in iteration k is denoted by Pi(k). Figure 1 shows the flowchart of ASO algorithm.
2.2. Planning Procedure for Movement
Each member has a planning process to decide how it will move and change his/her position in the next time. To this end, each member provides three movement policies and then combines them to find out his/her position in the next iteration. These movement policies are explained in three cases as follows:a) Movement policy choice based on the current position: The first movement policy in time k is denoted by MPicurrent(k) and is selected based of the current position. In general, the movement policy MPicurrent(k) is a neighboring method. The fickleness index FIi(k) is consider for member i in time k. This index is a measure of member i's dissatisfacation for his/her current situation, compared to other member's situations. When the objective function f is positive on S, FIi(k) for some nonnegative number αi in [0,1] is given as follows: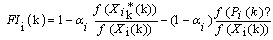 | (1) |
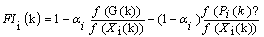 | (2) |
which are the numbers in the interval [0,1].● In the first case, EIi(k) is considered as the probability that member i will behave irregularly and generate his/her movement policy based on another randomly selected member’s position, which does not correspond to G-best.● In the second case, EIi(k) is compared with a threshold. If it is greater than the threshold, then member i will behave irregularly.The number EIi(k) can be defined according member i’s situation relative to G-best (or the i*kth member’s position) for some positive number θi as follows: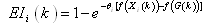 | (3) |
c) Movement policy choice based on past positions: The third movement policy in time k is represented by MPipast(k) and is selected based on the past positions that were visited by each member. It would be more common for each member to generate movement policy MPipast(k) based on P-best, but because the members are lawless, they may select any past position (or a number of them) to generate a movement policy. Thus, internal irregularity index IIi(k) is introduced for member i in time k, which can be used in the scenarios presented for EIi(k) in the previous case.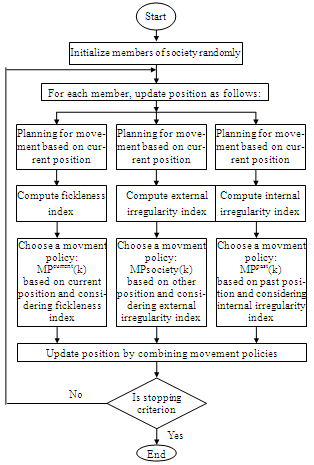 | Figure 1. Flowchart of ASO algorithm |
2.3. Combination Rule
After selecting movement policies MPcurrent(k), MPsociety(k), MPpast(k), each member must merge these policies to move toward a new position, so he/she requires a combination rule. The simplest method to this is to select the movement policy that yield the best new position, which is termed as elitism combination rule. An option is that the policies be applied sequentially on the current position; this may be called the sequential combination rule. Other types of combination rules can be defined according to the problem definition. Note that members may use different combination rules.
3. AVR System Modeling
The task of an AVR system is to hold the terminal voltage magnitude of a synchronous generator at a specified level. Thus, the stability of the AVR system would seriously affect the security of the power system. A simpler AVR system contains five basic components such as amplifier, exciter, generator, sensor and comparator. The real model of such a system is depicted in Fig. 2. A unit step response of this system without control has some oscillations which reduce the performance of the regulation. Thus, a control technique must be applied to the AVR system. For this reason, the PID block is connected to amplifier seriously. The A small signal model of this system including PID controller which is constituted through the transfer functions of these components is depicted in Fig. 3, and the limits of the parameters used in these transfer functions are presented in Table 1[3,6]. 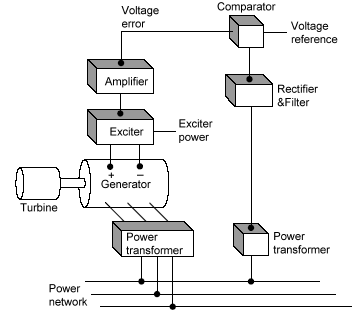 | Figure 2. A real model of AVR system[6] |
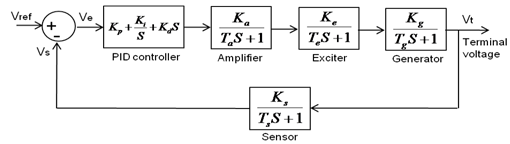 | Figure 3. Block diagram of AVR system |
Table 1. Parameters of AVR model with transfer function and parameter limits
 |
| |
|
4. ASO based PID Design
Nowadays, despite the significant developments of recent years in control theory and technology PID controllers are used in almost all sectors of industry and science such as AVR system[3-7]. This is because it performs well for a wide class of process. Also, they give robust performance for a wide range of operating conditions. Furthermore, they are easy to implement using analogue or digital hardware and familiar to engineers[9-10]. In this study, PID controller is used for the AVR system. It should be noted that the transient performance of the AVR system obviously depends on the optimal tuning of the PID controller's parameters. It is well know that the conventional methods to tune PID gains not able to locate or identify the global optimum for achieving the desired level of system robust performance due to the plant parameter changes and load disturbance of the power systems and also they may be tedious and time consuming. In order to overcome these drawbacks and provide optimal control performance, parallel ASO algorithm is proposed to optimal tune of PID gains under different operating conditions. Figure 4 shows the block diagram of ASO based tuned PID controller for the AVR system (Fig. 3). 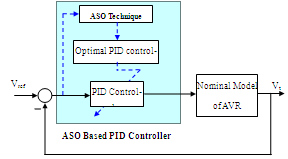 | Figure 4. The proposed ASO based PID controller structure |
By taking Ve as the system output, the control vector for PID controller in each control area is given by: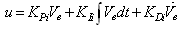 | (4) |
The gains KPi, KIi and KDi are tuned using ASO technique and then, the PID controller generates the control signal that applies to the amplifier to control the generator field winding by exciter. In this study, the ASO module works offline. In [4], Gain has taken the generator transfer function as Kg/(1+Tgs) where Kg depends on load (0.7–1.0) and 1.0 s≤Tg ≤2.0 s. Thus, to illustrate the capability of the proposed strategy, in the view point of uncertainty our focus will be concentrated on variation of these parameters. It should be noted that choice of the properly objective function is very important in synthesis procedure for achieving the desired level of system robust performance. Because different objective functions promote different ASO behaviors, which generate fitness value providing a performance measure of the problem considered. In general, the integrated of absolute error (IAE) or the integral of squared-error (ISE) or the integrated of time- weighted-squared-error (ITSE) is often utilized for the PID controller design. However, the minimization of IAE and ISE criteria can result in a response with relatively small overshoot but a long settling time, because the ISE performance criterion weights all errors equally independent of time. Although, the ITSE performance criterion can overcome the disadvantage of the ISE criterion, the derivation processes of the analytical formula are complex and time-consuming[11]. In this paper, a new performance criterion in the time domain is proposed under multiple operation points that optimized by using of ASO technique. It includes overshoot (OS), settling time (Ts) and maximum rate of system response (max-dv) and is considered as follows: 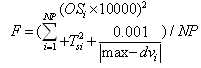 | (5) |
Where, OSj, TSi and Vi are Overshoot, settling time and terminal voltage of AVR system for ith operating points. NP is the total number of operating points for which the optimization is carried out. In this fitness function, the overshoot is considered for achieving dynamical robust performance of system and the other part is added to objective function for increasing of system speed. The multiple operating conditions for the system are completely defined by changing the values of the Kg and the Tg parameters in the AVR system. These parameters are assumed to vary independently over the following ranges:● Kg changes from 0.7 to 1.0 by step 0.1● Tg: 1.0 from to 2.0 by step 0.1This encompasses almost all practically occurring operating conditions with changes system load from full load to no load case. For objective function calculation, the time-domain simulation of the power system model is carried out for the simulation period. It is aimed to minimize this objective function in order to improve the system response in terms of the settling time and overshoots. Thus, the design problem can be formulated as the following constrained optimization problem, where the constraints are the PID gains bounds.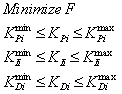 | (6) |
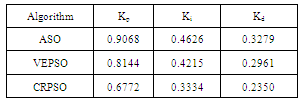
Typical ranges of the optimized parameters are [0.1-2]. To improve the overall system dynamical performance in a robust way and optimization synthesis, this paper utilizes ASO technique to solve the above multi objective optimization problem and search for optimal or near optimal set of PID controller parameters. It should be noted that ASO algorithm is run several times and then off-nominal optimal set of controller parameters is selected. The optimization of PID controller parameters is carried out by evaluating the objective cost function as given in Eq. (5), which considers a multiple of operating conditions. Consider that in the AVR system Ka, Ta, Ke, Te and Ts are 10, 0.1, 1, 0.4 and 0.01, respectively and a step value 0.01 is applied for reference voltage. The final values of the optimized parameters using ASO, CRPSO[3] and VEPSO[7] techniques are given in Table 2. Also, Fig. 5 shows the fitness convergence by ASO method.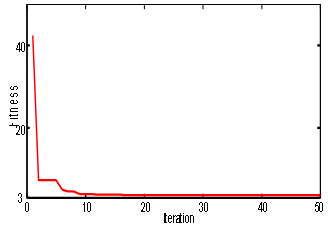 | Figure 5. Fitness convergence in ASO method |
Table 2. Optimized parameters of PID controller
 |
| |
|
5. Simulation Results
The proposed ASO based tuned PID controller is applied for AVR system shown in Fig. 3 and compared with optimized PID controller using VEPSO and CRPSO method. To demonstrate robustness of the proposed control strategy against parametric uncertainties simulations are carried out for five number of operating conditions is considered as follows:● Case 1: Kg=0.7, Tg=1● Case 2: Kg=0.8, Tg=1.6● Case 3: Kg=0.9, Tg=1.4● Case 4: Kg=0.9, Tg=2● Case 5: Kg=1, Tg=2The system response using the ASO, VEPSO and CRPSO based designed PID controller is shown in Fig. 6-10 for different operation conditions (Case 1- Case 5). It can be seen that the performance of the ASO based tuned PID controller is quite prominent in comparison with the SPSA based PID controller and the overshoots and settling time are significantly improved for the AVR system. Also, it is superior to the VEPSO and CRPSO approaches.To demonstrate performance robustness of the proposed method, two performance indices: the ITAE and Figure of Demerit (FD) based on the system performance characteristics are defined as [12]: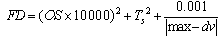 | (7) |
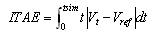 | (8) |
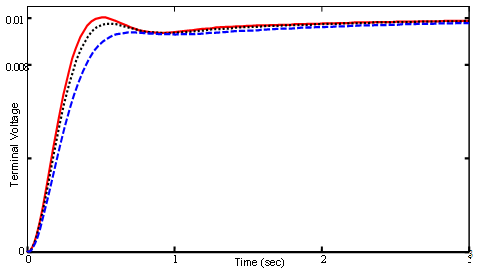 | Figure 6. Terminal voltage deviation of AVR for case 1; Solid (ASO), Dotted (VEPSO) and Dashed (CRPSO) |
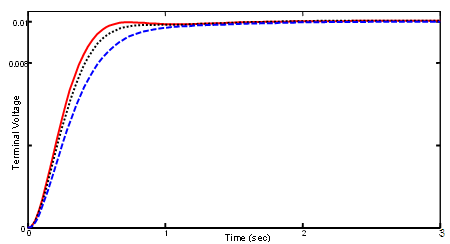 | Figure 7. Terminal voltage deviation of AVR for case 2; Solid (ASO), Dotted (VEPSO) and Dashed (CRPSO) |
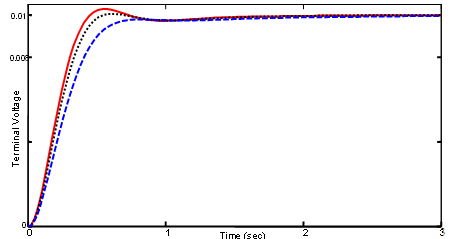 | Figure 8. Terminal voltage deviation of AVR for case 3; Solid (ASO), Dotted (VEPSO) and Dashed (CRPSO) |
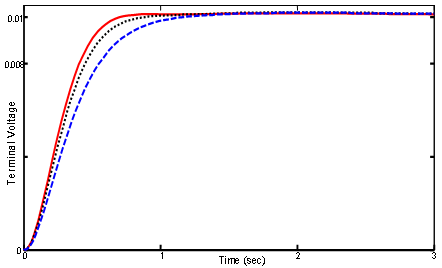 | Figure 9. Terminal voltage deviation of AVR for case 4; Solid (ASO), Dotted (VEPSO) and Dashed (CRPSO) |
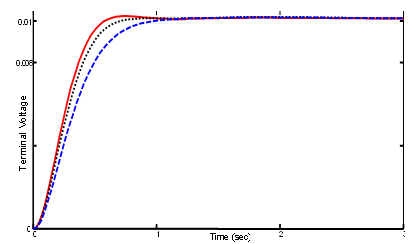 | Figure 10. Terminal voltage deviation of AVR for case 5; Solid (ASO), Dotted (VEPSO) and Dashed (CRPSO) |
Numerical results of performance robustness for all operation cases are shown in Figs. 11 and 12. It can be seen that the values of these system performance characteristics with the proposed ASO based tuned controller are much smaller compared to that CRPSO and VEPSO based designed controller. This demonstrates that the overshoot, settling time and system response speed is greatly reduced by applying the optimized controller using the proposed optimization strategy.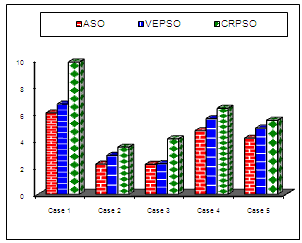 | Figure 11. Value of ITAE using three methods |
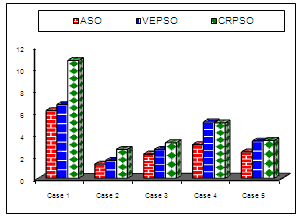 | Figure 12. Value of FD using three methods |
6. Conclusions
This paper presents a novel and effective optimization algorithm to PID control design of AVR system using the ASO algorithm in order to improve electromechanical oscillations in a power system. The main feature of ASO is that it converges in the limit to a globally optimal solution with probability one under mild conditions. The proposed method integrates the ASO algorithm with the new time-domain performance criterion into an ASO-PID controller. The problem of optimal tuning of PID gains is formulated as an objective optimization problem for a wide range of uncertain plant parameter changes. The results showed that the proposed approach is efficient to tune PID controller for AVR system. The effectiveness of the proposed controller has been tested in comparison with CRPSO and VEPSO methods through the simulation studies and some performance indices under different operating conditions. Results analysis show that the proposed method led to an improvement of the system characteristic such as overshoot, settling time and system response speed than the other recently reported methods in literature.
References
| [1] | P. Kundur, “Power system stability and control”, New York: McGrew Hill, USA, 1994. |
| [2] | H. Saadat, “Power system analysis”, New York: McGrew Hill, USA, 1999. |
| [3] | V. Mukherjee, S.P. Ghoshal, “Intelligent particle swarm optimized fuzzy PID controller for AVR system”, Electric Power Systems Research, Vol. 77, pp.1689-1698, 2007. |
| [4] | Z.L. Gaing, “A particle swarm optimization approach for optimum design of PID controller in AVR system”, IEEE Transactions on Energy Conversion, Vol. 19, No. 2, pp. 348-391, 2004. |
| [5] | D.H. Kim, J.H. Cho, “A biologically inspired intelligent PID controller tuning for AVR systems”, International Journal of Control Automatic and Systems, Vol. 4, pp. 624-636, 2006. |
| [6] | H. Gozde, M.C. Taplamacioglu, “Application Of artificial bee colony algorithm in an automatic voltage regulator (AVR) system”, International Journal on Technical and Physical Problems of Engineering, Vol. 1, No. 3, pp. 88-92, 2010. |
| [7] | H. Shayeghi, H.A. Shayanfar, M. Ghasemi, A. Tohidi, “PID controller design for AVR system using parallel vector evaluated particle swarm optimization”, In Proc. of the 7th International Conference on Technical and Physical Problems of Engineering, Lefkosa, TR Northern Cyprus, pp. 211-216. |
| [8] | A. Ahmadi-Javid, “Anarchic society optimization: a human-inspired method, Applied Soft Computing”, In Proc. of IEEE Congress on Evolutionary Computation, pp. 2586-2592, New Orleans, LA, 2011. |
| [9] | H. Shayeghi, H.A. Shayanfar, A. Ghasemi, “PID type stabilizer design for multi machine power system using IPSO procedure, ” Computer Science and Engineering, vol. 1, pp. 36-42, 2011. |
| [10] | H. Shayeghi and A. Ghasemi, “Market based LFC design using artificial bee colony”, International Journal on Technical and Physical Problems of Engineering, Vol. 3, pp. 1-10, 2011. |
| [11] | R. A. Krohling and J. P. Rey, “Design of optimal disturbance rejection PID controllers using genetic algorithm,” IEEE Trans. on Evolutionary Computation, Vol. 5, pp. 78-82, Feb. 2001. |
| [12] | H. Shayeghi, H.A. Shayanfar, S. Jalilzadeh, A. Safari, “TCSC Robust damping controller design based on particle swarm optimization for a multi-machine power system”, Energy Conversion and Management, Vol. 51, pp. 1873-1882, 2010. |

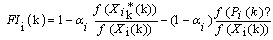
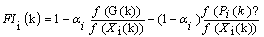
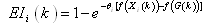




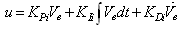
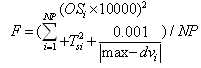
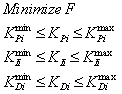

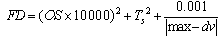
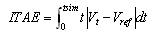







 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML
