Abir Belgacem 1, Houssem Jerbi 2, Mohamed Naceur Abdkerim 1
1Research Unit Modeling, Analysis and Control of Systems, National Engineering School of Gabes, Gabes, 6029, Tunisia
2Laboratory Study of Automatic Control and Process, National Engineering School of Gabes, Gabes, 6029, Tunisia
Correspondence to: Abir Belgacem , Research Unit Modeling, Analysis and Control of Systems, National Engineering School of Gabes, Gabes, 6029, Tunisia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper a flatness approach to fault parameter detection is proposed. Our main contribution in this work consists in the synthesis of a flat moving horizon estimator for a supervision industrial process. The effectiveness of the proposed method is shown through the supervise of a series DC motor. The obtained results are very satisfactory in terms of detection rapidity and precision relatively to the case where the classic state estimator is adopted.
Keywords:
Fault Parametric Detection, Optimisation, Flatness, Flat Moving Horizon Estimator, Serie’s DC Motor
1. Introduction
Fault detection and diagnosis can affect the performances of the industrial processes. A simple fault can reduce their productivity and their competitiveness. In this way, it’s necessary to apply a fault detection and diagnosis scheme to reduce the incurred risks. On the other hand, it is so important to reduce the time of detection to come up with reliable decision on line. Several fault detection approaches are described in literature[9,10]. Particularly the fault detection based on parameter estimation proposed by Isermann[2].This later based on changing process parameters, which are not directly measurable, requires on line parameter estimator such as Moving Horizon Estimator (MHE)[6].In this paper two fault detection approaches based on parameter estimator MHE are compared.The MHE estimator is applied to the direct differential model of the system to detect the variation of the parameters. Then the same estimator is applied to the flat differential model of the system, using the property of flatness of the studied dynamical process. The present paper is organized as follows: Section 2 is reserved to introduce the identification method. In section 3, numerical simulations are presented where a comparison between the two approaches is included. This paper will be closed by the main concluding remarks.
2. Identification Method
2.1. Flatness Concept
Consider a nonlinear system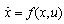 | (1) |
This system is flat if there is a vector of outputs such as states and system commands can be determined from the vector of outputs and a finite number of its derivatives[1,3]. Thus, no integration of differential equations is made necessary: the trajectories of states and inputs of the system can be immediately obtained from the trajectories of flat outputs[1,3].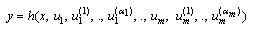 | (2) |
Such as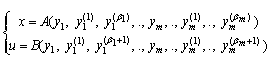 | (3) |
WhereA, B: Vector valued function A = (A1, ....., An), B = (B1, ......, Bm).
2.2. Model Method
The model method[4,5] based on the comparison between experimental results and simulations response. This method is classified among the methods are based on the minimization of a quadratic criterion: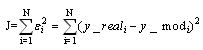 | (4) |
Whereu: is the input vector of the systemyreal: is the output vector of the processymod: is the model output vector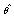 : is the parameters vector
: is the parameters vector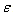 : is the error vector between the measured output and estimated output.J: is the criterion to be minimized by a nonlinear programming algorithm (PNL)[4]. In this paper we used the Levenberg-Marquardt algorithm.
: is the error vector between the measured output and estimated output.J: is the criterion to be minimized by a nonlinear programming algorithm (PNL)[4]. In this paper we used the Levenberg-Marquardt algorithm.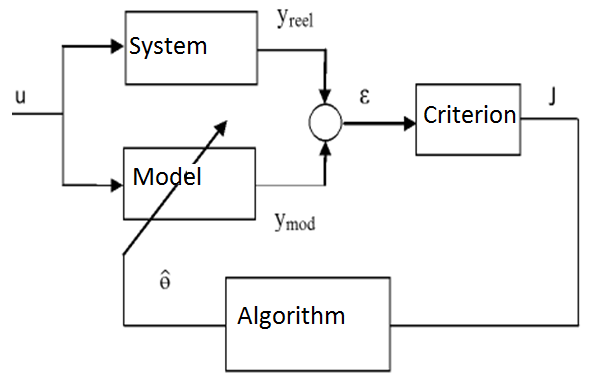 | Figure 1. Principle of identification method |
2.2.1. Estimator Algorithme
The Levenberg-Marquardt[13] defines the next update 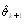 as following:
as following: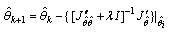 | (5) |
Where I is the identity matrix, λ is a regularization parameter, which controls both the search direction and the magnitude of the next update 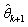 and
and 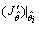 is the Jacobian matrix.The first derivate of J is given by:
is the Jacobian matrix.The first derivate of J is given by: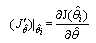 | (6) |
The second derivate of J is expressed by: 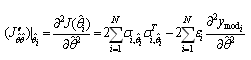 | (7) |
The approximation of Newton, we allow to eliminate this term 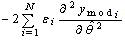 in the Hessian expression. So the expression of Hessian become
in the Hessian expression. So the expression of Hessian become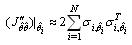 | (8) |
Where 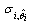 is the vector of sensitive functions[4,7].
is the vector of sensitive functions[4,7].
2.3. The Moving Horizon State Estimation Concept
The basic concept of the moving horizon method will be presented in this section. The basic idea in the moving horizon estimation (MHE) approach is to maintain a constant length of the estimation window by discarding the oldest sample as a new measurement becomes available[6].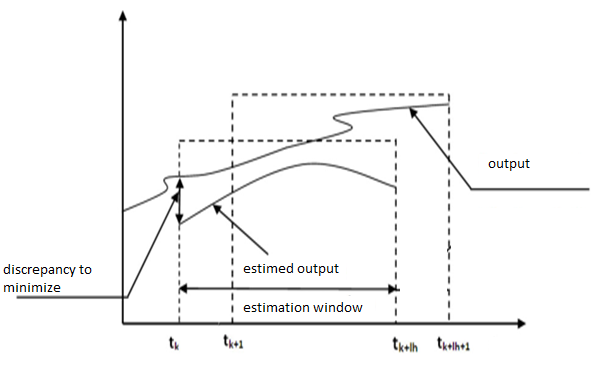 | Figure 2. Principle of the moving horizon estimator |
3. Identification Example and Simulation Results
We illustrate the effectiveness of the proposed approach via a simulation study leaded on the nonlinear model of a series DC motor. Neglecting magnetic saturation in the field circuit, a series DC motor can be modelled as[12]: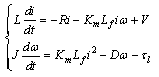 | (9) |
where i represent the armature current, V is the input of the system, w is the rotational speed of the motor, R is the armature and the field resistance, Lf is the armature and the field resistance, J is the moment of inertia associated with both motor and the load, Km is the motor constant, D is the viscous friction coefficient and τL is the load torque.
3.1. Flat Model of the Serie’s DC Motor
The basic idea of the identification method using the flat model is presented as follow: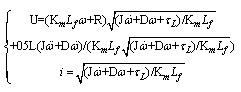 | (10) |
To determine the derivatives of the rotational speed, we use an approximate derivation algorithm based on Lagrangian interpolation polynomial form. This later using five points[11]. The general expression of derivation formula is given in[8] and it’s valid for n point.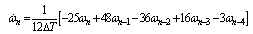 | (11) |
3.2. Results and Discussion
The motor data used in simulations is given in table 1.In order to illustrate the performance of the flat estimator for fault detection, we have compared it with the classic moving state estimator. As the Levenerg-Marquardt algorithm requires initialization parameters to be estimated close to real ones, we initialized the parameters to be estimated at 10% of the real values. In addition, the initial regularization parameter λ is chosen equal to 1 and the length of the horizon is set equal to 4∆T[14] avec ∆T = 0.05s.| Table 1. Series DC motor parameters |
| | R | 7.2 Ω | | L | 0.0917 H | | D | 0.0004 N.m/rad/s | | K | 0.1236 N.m/Wb.A | | J | 0.0007046 Kg-m2 |
|
|
Figure 3 present the evolutions of the electric parameter for the flat model of the motor. It shows clearly a rapidity of convergence of parameters. This result is expected because the optimisation algorithm doesn’t necessity a numerical integration algorithm.In order to test the robustness of the moving horizon estimator based on the Levenberg-Marquardt algorithm applied to the flat model, we introduced a white noise characterized by a zero mean and a variance equal to 10 ^ -3, to the output of the system.Figure 4 describe the evolution of electrical parameters of the motor. A static discrepancy is observed in the case of the estimate of the inductor. This is justified by the very low sensitivity of the inductance to the system output. 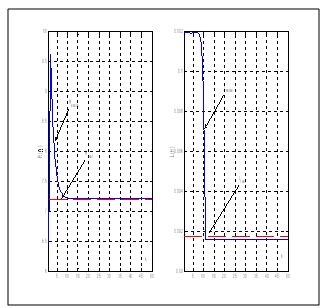 | Figure 3. Evolution of the electrical parameter for the flat model |
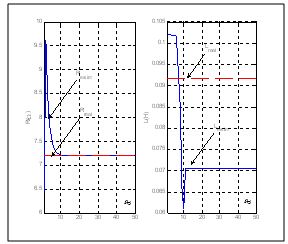 | Figure 4. Evolution of the electrical parameter for the flat model (introduced the white noise) |
Figures 5 and 6 present the evolutions of the viscous friction coefficient and the quadratic criterion for the classic state estimator. These figures show the detection of the deviation of the parameter. However, this estimator requires a time, relatively, important to ensure the convergence of the parameters.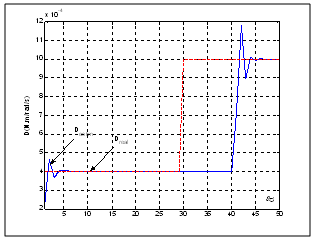 | Figure 5. Evolution of the viscous friction coefficient for the direct model of the motor (fault in the viscous friction coefficient) |
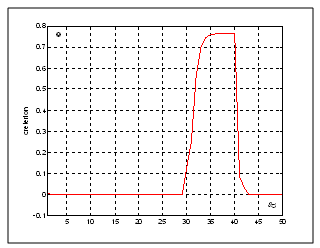 | Figure 6. Evolution of the quadratic criterion for the direct model of the motor (fault in the viscous friction coefficient) |
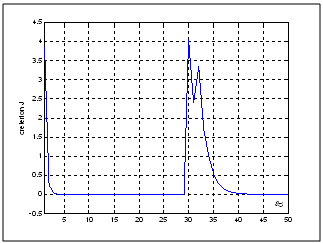
Compared to previous results (Figures 5 and 6), the results, illustrated by figures 7 and 8, clearly show better performance. The simulation results confirm that the flat estimator offers a rapid and perfect detection of the deviation of the parameters.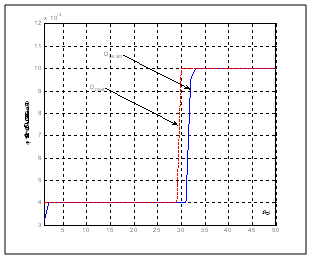 | Figure 7. Evolution of the viscous friction coefficient for the flat model of the motor (fault in the viscous friction coefficient) |
 | Figure 8. Evolution of the quadratic criterion for the flat model of the motor (fault in the viscous friction coefficient) |
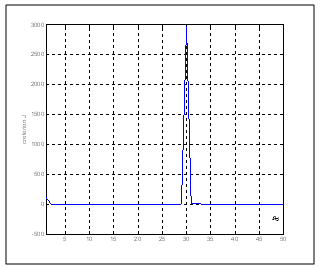
Figures 9 and 10 describe, respectively, the evolution of the equivalent resistance R and the quadratic criterion J in the case where the moaving horizon estimator is applied to the system. These figures show acceptable performance in terms of detection of the deviation of the parameters. Figures 11 and 12 show, respectively, the evolution of the equivalent resistance R and the quadratic criterion J in the case where the moving horizon estimator is applied to the flat system. It is clear that performances are best recorded in terms of detection of the deviation parameter. This result is actually expected since the estimator is applied to the synthesized flat model of the system.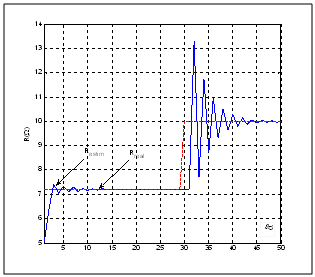 | Figure 9. Evolution of the equivalent resistance for the direct model of the motor (fault in the equivalent resistance) |
 | Figure 10. Evolution of the quadratic criterion for the direct model of the motor (fault in the equivalent resistance) |
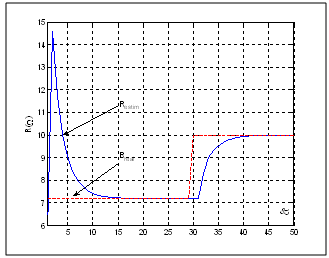 | Figure 11. Evolution of the equivalent resistance for the flat model of the motor (fault in the equivalent resistance) |
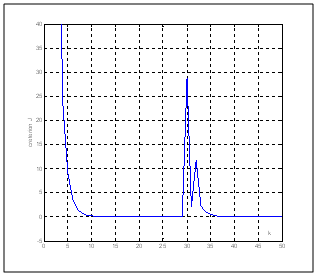 | Figure 12. Evolution of the quadratic criterion for the flat model of the motor (fault in the equivalent resistance) |
4. Conclusions
We have synthesized in this paper a flat moving horizon estimator for detection parameter fault. In fact, the implementation on line of a moving horizon state estimator necessities a reduce time. To achieve this goal, we introduced the proprieties of flatness. The obtained results, for the flat estimator are very satisfactory in terms of detection rapidity and precision.
References
| [1] | M. Fliess, J. L´evine, P. Martin and P. Rouchon, Flatness and defect of nonlinear systems: Introductory Theory and examples. International Journal of Control, Vol. 61, no. 6, pp. 1327-1361, 1995. |
| [2] | R. Iserman, Estimation of physical parameters for dynamic processes with application to an industrial robot. International Journal of Control, Vol. 55, no. 6, pp. 1287-1298, 1992. |
| [3] | P. Martin, Contribution à l’étude des systèmes différentielle ment plats. PhD thesis. Institut National Polytechnique de Lorraine. 1992. |
| [4] | J. Richalet, A. Rault and R. Pouliquen, Identification des processus pour la méthode du modèle. Rout Ledge, 1971. |
| [5] | E. Walter et L. Pronzato. Identification of parametric models from expremental data. Springer, 1997. |
| [6] | H. Valdes, Contribution à l’estimation d’état `a horizon Glissant par méthodes ensembles: Application à la surveillance et détection des dysfonctionnements sur des bioprocédés. PhD thesis, Université Joseph Fourier Grenoble, 2002. |
| [7] | J. C Trigeassou, S. Bachir and S. Tnani Diagnostic by parameter estimation of stator and rotor faults occurring in induction machines. IEEE Transactions on Industrial Electronics, vol.53, no.3, pp.963-973, 2006. |
| [8] | S. Demidovitch, I. Maron, Elements de calcul numérique , Ed, Mir, Moscou. |
| [9] | S. Qin, W. Li, Detection and identification of faulty sensors in dynamic processes. A.I.Ch.E. Journal, 47, 1581˝ U1593, 2001. |
| [10] | W. Li and S. Shah, Structured residual vector-based approach to sensor fault detection and isolation. Journal of Process Control, 12, 429˝U443, 2002. |
| [11] | A. Sanchez, Approche non linéaire de la commande en contraction d’un muscle artificiel pneumatique de McKibben. PhD thesis, Institut National des Sciences Appliquées de Toulouse, 2000. |
| [12] | S. Mehta and J. Chiasson, Nonlinear control of a series DC moteur: Theory and experiment. IEEE Trans, on industrial electronics, Vol. 45, No. 1, pp. 134-141, 1998. |
| [13] | F. Khatounian, Contribution à la modélisation,l’identification et la commande d’une interface haptique à un degré de liberté entrainée par une machine synchrone à aimants permanents. PhD thesis, Ecole normale supérieure de Cachan, 2006. |
| [14] | H. Valdes, Contrubition à l’estimation d’état à horizon Glissant par méthodes ensembles: Application à la surveillance et détection des dysfonctionnements sur des bioprocédés. PhD thesis, University Joseph Fourier Grenoble, 2002. |

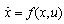
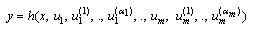
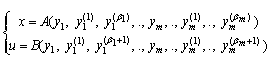
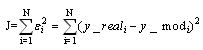
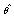 : is the parameters vector
: is the parameters vector : is the error vector between the measured output and estimated output.J: is the criterion to be minimized by a nonlinear programming algorithm (PNL)[4]. In this paper we used the Levenberg-Marquardt algorithm.
: is the error vector between the measured output and estimated output.J: is the criterion to be minimized by a nonlinear programming algorithm (PNL)[4]. In this paper we used the Levenberg-Marquardt algorithm.
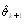 as following:
as following: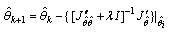
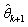 and
and 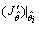 is the Jacobian matrix.The first derivate of J is given by:
is the Jacobian matrix.The first derivate of J is given by: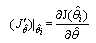
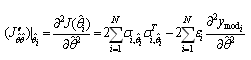
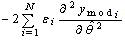 in the Hessian expression. So the expression of Hessian become
in the Hessian expression. So the expression of Hessian become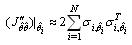
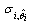 is the vector of sensitive functions[4,7].
is the vector of sensitive functions[4,7].
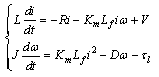
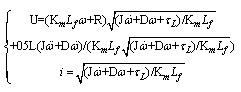
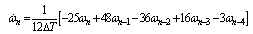










 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML