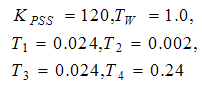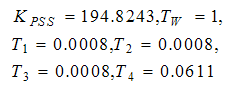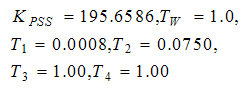1. Introduction

Transient and dynamic stabilities are the most important issues in the reliable and efficient operation of power sys-tems. The generators are equipped with the Power System Stabilizers (PSSs), as supplementary control devices, to provide the extra damping and the good dynamic perform-ance. Conventional power system stabilizers (CPSS) are designed using the theory of phase compensation in the frequency domain and are introduced as a lead-lag phase compensator. Parameters of CPSS are determined based on a linearized model of the power system.

The power system behaves highly nonlinearly, with con-figurations and parameters that change with time; so the CPSS design based on a linearized model cannot guarantee its performance in a practical operating environment. If parameters of PSS are tuned by speed deviation in each generator when a disturbance occurs at a bus or line, the power system will have a good performance. Hence, several PSS design techniques are reported in literature, a few are listed in the references[1-11]. The mentioned local optimization techniques providing the optimum PSS parameters need a target function. Some optimization techniques that are designed using theory of phase compensation in the frequency domain tune parameters of PSSs in response to an existing mode or some modes of oscillations in the system, but techniques like Genetic Algorithms (GAs) [7,15,16], Tabu search Algorithm[8], Simulated Annealing[9], Particle Swarm Optimization (PSO) algorithm[12] and Bacterial Foraging Algorithm (BFA)[13] provide damping for all modes of oscillation in the system. Objective function used in these methods must be chosen with care. The target function is called objective function and it must vary when the parameters and speed of generators change. In references[12,13], several objective functions are described. Procedure and results of the optimization in every repetition with the objective functions in these references shows that the objective functions cannot attain expected response. To solve the mentioned problem, in this paper, a new objective function is used which is Samples Magnitude Values Sum in DFT (SMVS-DFT). SMVS-DFT of the deviation speed is obtained and regarded as objective function. The objective function is lower in systems with low speed deviation and higher in systems with high speed deviation. Fast Fourier Transform is an algorithm to compute Discrete Fourier transform (DFT). A Particle Swarm Optimization (PSO) algorithm[10] and Imperialist Competitive Algorithm (ICA) have been proposed in this paper as the optimization algo-rithms and they use to the SMVS-DFT of the speed devia-tion as objective function.

The paper is organized as follows: Section 2 presents the power system and the PSS considered in this study; Section 3 describes the PSO algorithm and ICA; Section 4 describes objective function used in determining the optimal parame-ters of the PSS; Section 5 presents some simulation results obtained using the PSO algorithm and ICA and it highlights the benefits of the SMVS-DFT used in the PSO algorithm and ICA compared with CPSS and the previously used ob-jective function in PSO and ICA to design the PSS.Finally, conclusions are presented in Section 6.

2. Power System

2.1. Power system Model

The system of our study is the one machine infinited to infinite bus system shown in Figure 1. The external line parameters, 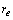and 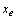are to be varied with the changes in the electrical strength of the connection and the length of the line between generator and infinite bus. The operating conditions are chosen in this study as

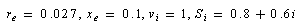Where 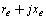is the impedance value of the RL line connecting the generator to the infinite bus. 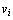and 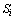are voltage and delivered complex power at the infinite bus for it to establish condition.[21]

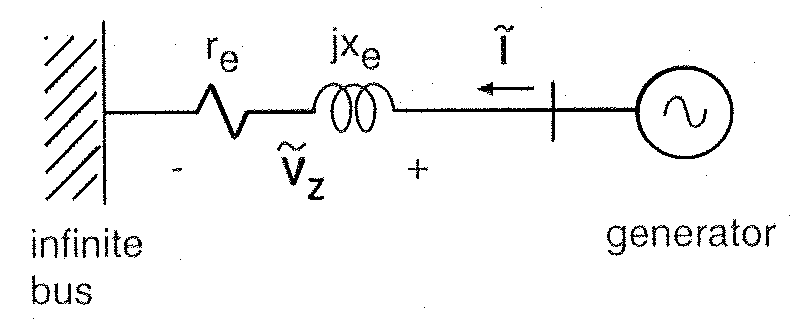Figure 1. One machine to infinite bus system.

2.2. PSS

The block diagram of the typical PSS used in this study is depicted in Figure 2. The signal washout is a high-pass filter that prevents steady changes in speed from modifying the field voltage. For the low-frequency oscillations, a washout time constant is usually selected in range 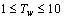, since lower-time constants result in significant phase lead at low frequencies which will reduce the synchronizing torque component at intra-area frequencies[1]. The desynchronising effect is detrimental to intra-area and local transient stability. The parameters for the phase compensation blocks and PSS gain were determined by the tuning procedure while in CPSS the PSS gain is selected based on the root locus analysis.

Figure 2. Block diagram of the power system stabilizer.

3. Optimization Algorithms

3.1. Particle Swarm Optimization (PSO)

The PSO was first introduced by Kennedy and Eberhart[14]. It is one of the optimization techniques and a kind of evolutionary computation technique. Social behavioural pattern of organisms such as bird flocking or fish schooling inspired them to look into the effect of collaboration of species when achieving their goals as a group. It is based on a simple concept. Therefore, the computation time is short and requires few memories. It was originally developed for nonlinear optimization problems with continuous variables. The PSO is basically developed through simulation of bird flocking. The position of each particle is shown by n-dimensional vector 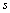and the velocity of each particle is presented by n-dimensional vector . The position corresponding to the best fitness is known as 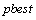and the overall best out of all the particles in the population is called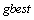. The modified velocity and position of each particle in each situation is calculated using the velocity, position and 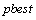of each particle and 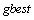of the particles in the previous situation. The distance from the 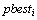to 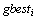as shown in the following formulas.[14]

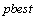and 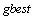are determined by the objective function used in typical problem. Position of each particle includes parameters that evaluate objective function. Namely, each particle tries to modify its position using the following information:

The current positions

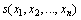The current velocities

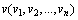The distance between the current position and pbest

The distance between the current position and gbest

This modification can be represented by the concept of velocity. Velocity of each particle can be modified by the following equation:

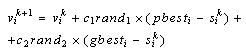(1)

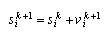(2)

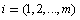
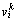: Vector of velocity of particle 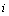at iteration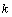

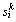: Vector of current position of particle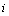at iteration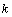

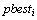: Vector of 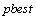of particle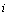

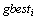: Vector of 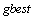of all particles

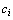: Weighting factor

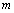: Number of the particles

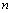: Number of the parameters of each particle and typical problem

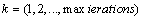: Number of iteration to arrive to the best answer and objective function.

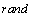: Random number between 0 and 1

Using (1) the new velocity of the particles which gradually gets close to 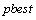and 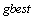is calculated.

Using (2) position can be modified.

3.2. Imperialist Competitive Algorithm (ICA)

is an algorithm for optimization inspired by the imperialistic competition. Like other evolutionary ones, the proposed algorithm starts with an initial population. Population individuals called country are in two types: colonies and imperialists that all together form some empires. Imperialistic competition among these empires forms the basis of the proposed evolutionary algorithm. During this competition, weak empires collapse and powerful ones take possession of their colonies. Imperialistic competition hopefully converges to a state in which there exists only one empire and its colonies are in the same position and have the same cost as the imperialist[22].

After dividing all colonies among imperialists and creating the initial empires, these colonies start moving toward their relevant imperialist country. This movement is a simple model of assimilation policy that was perused by some imperialist states[24]. Figure 3 shows the movement of a colony towards the imperialist. In this movement, 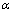and x are random numbers with uniform distribution and d is the distance between colony and the imperialist[23].

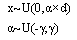(3)

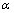In (3) and 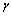are arbitrary numbers that modify the area that colonies randomly search around the imperialist. In our implementation 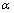and 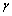are 2 and π/4 (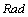) respectively. The total power of an empire depends on both the power of the imperialist country and the power of its colonies. In this algorithm, this fact is modeled by defining the total power of an empire by the power of imperialist state plus a percentage of the mean power of its colonies. Any empire that is not able to succeed in imperialist competition and cannot increase its power (or at least prevent decreasing its power) will be eliminated. The imperialistic competition will gradually result in an increase in the power of great empires and a decrease in the power of weaker ones. Weak empires will lose their power gradually and ultimately they will collapse. The movement of colonies toward their relevant imperialists along with competition among empires and also collapse mechanism will hopefully cause all the countries to converge to a state in which there exist just one empire in the world and all the other countries are its colonies. In this ideal new world colonies have the same position and power as the imperialist.

In this research the Imperialist Competitive Algorithm (ICA) is used to tune parameters of the PSS. Figure 4 depicts the flowchart of ICA[22, 23].

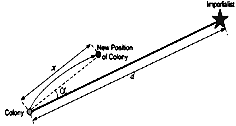Figure 3. Motion of colonies toward their relevant imperialist.

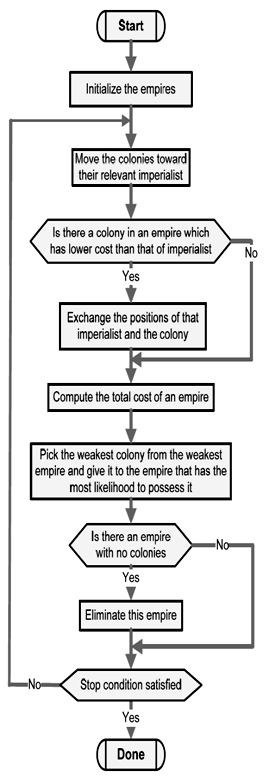Figure 4. Flowchart of the Imperialist Competitive Algorithm.

4. Objective Function

Fourier transform is a fine analysis for both continuous-time and discrete signals in analogous ways. The definition of the continuous-time Fourier transform is explained by

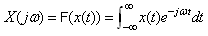(4)

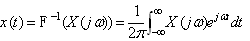(5)

The definition of the discrete-time Fourier transform is explained by

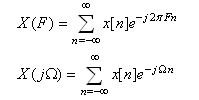(6)

The condition for convergence of the discrete-time Fourier transform is simply that the summation in

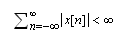(7)

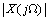actually convergence. If is bounded, the inverse transform

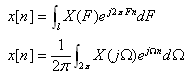(8)

will always converge because the integration interval is finite. The most commonly used Fourier analysis technique in the world is the so-called Fast Fourier transform which is an efficient algorithm for computing the discrete Fourier transform (DFT). The DFT is almost identical to the discrete Fourier transform sample (DTFS). The only real differences are a scaling factor and an assumption that the first sample of continuous-time signal occurs at time. 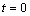The DTFS of a set of samples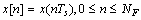, from a continuous-time signal x(t) is defined by transform pair

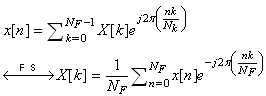(9)

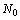The DTFS harmonic function X[k] is periodic with fundamental period and in general, the representation is only valid for. If x[n] is periodic with fundamental period and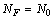, then the representation 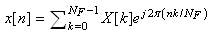is valid for any n.

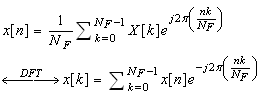(10)

So

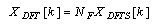(11)

And

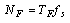(12)

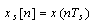(13)

At the final, we have

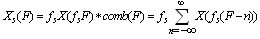(14)

In 1965 Cooley and Tukey popularized an algorithm which is much more efficient in computing time for large input arrays whose length is an integer power of 2. This algorithm for computing the DFT is the so-called fast Fourier transform (FFT).[17]

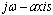The Fourier transform of a signal is the transform evaluated on the . With consider the class of second-order systems, the frequency response for the system, originally is given in (15).

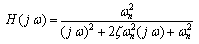(15)

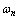Where is undamped natural frequency and 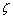is damping ratio.

For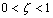, the poles in (15) are complex, so the impulse response and step response have oscillatory parts. Two poles occur in complex conjugate locations. When 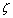is small, the poles are close to the 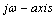as 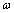approaches 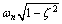and the behavior of the frequency response is dominated by the pole vector in the second quadrant and the length of that pole vector has a minimum at 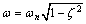. Thus, it would be expected the magnitude of the frequency response to exhibit a peak of the vicinity of that frequency. Because of the presence of the other pole, the peak will happen not exactly at 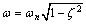but at a frequency less than this value will happen. A careful sketch of the magnitude of the frequency response for 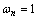and several values of 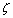is presented in Fig. 5. Therefore, the second-order system is a nominated band pass filter, with the parameter 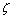controlling the sharpness and width of the peak in the frequency response. For small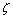, and abdicating the effect of the distant third-quadrant pole, 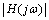is within a factor of 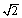of its peak value over the frequency range

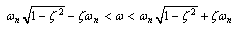(16)

Frequency response can be estimated by utilizing Figure 5. The responses of these systems can be approximated by dominant roots of the second-order system as long as the real part of the dominant roots is small percentage of the real part of the other roots[19]. Thus, the dominant poles can evaluate overshoot, settling time and define step response of the system.

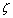So, if is closer to zero, the peak in the frequency response will be sharper and narrower. Thus the result of the argument is: if 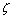increases from 0 toward 1, the relative bandwidth of the frequency response will increase, and the frequency response will become less sharp and less frequency selective[18]. Third-order systems and n-order systems possess a dominant pair of poles and the step response depends on the poles.

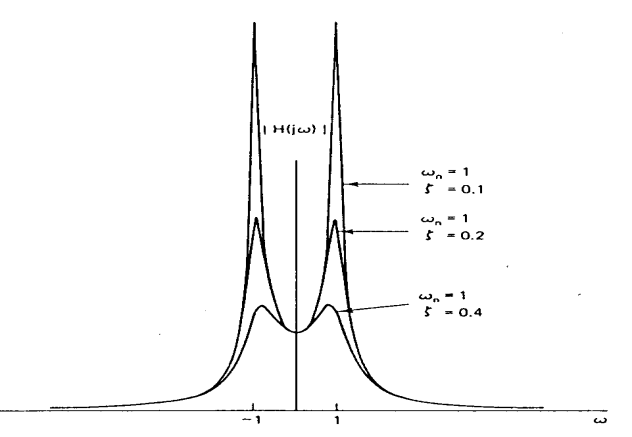Figure 5. Magnitude of the second frequency for the second order system.

We can use speed deviation of the generator as control signal and compute DFT of the control signal using the operation FFT algorithm. The frequency response behaviour and the decrease and increase of each sample magnitude in the DFT with and show that the sums of the values of the magnitude of the samples in discrete Fourier transform (Samples Magnitude Values Sum in the DFT) can be a good criterion for the evaluation of the Fourier transform and generator speed deviation. Therefore, we can use the SMVS-DFT as objective function.

5. Obtained Results Using the PSO and ICA

The results of the simulation and optimization have been obtained using MATLAB software. Fault which occurs is entered in power system as a disturbance. Fault is added to the mechanical power as disturbance of the power. Values disturbance are and are applied in the system in several times as below

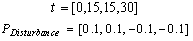
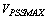and 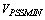have been modified so these parameters are chosen as below 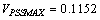and 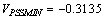correctively considered reference[20].The PSS parameters obtained and tuned by PSO and have been showed in Table1. PSS parameters calculated in[21] also is presented in this Table 1.

Figure 8 shows deviation speed of the generator in two states; without PSS and calculated parameters of the PSS by the CPSS (conventional power system stabilizer). It can be seen that the damping with CPSS is better than without PSS. Figure 9 shows deviation speed of the generator in two states; tuned parameters of the PSS by the PSO and calculated parameters of the PSS by the CPSS. It can be seen that the damping with PSS based on PSO is better than that of based on CPSS.

Table 1. PSS parameters calculated with various methods Method PSS PARAMETERS CPSS PSO ICA

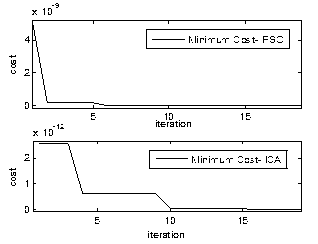Figure 6. Minimum costs of countries and PSO particles versus iterations.

Figure 10 shows deviation speed of the generator in two states; tuned parameters of the PSS by the ICA and tuned parameters of the PSS by the PSO. It can be seen that the damping with PSS based on is better than that of based on PSO In the final. Figure 6 presents minimum costs of countries and PSO particles versus iterations and the convergence rate for both of the algorithm show. The comparison results that reaches less values of error probability. It can clearly be seen that and PSO algorithm and using this objective function converge rapidly. Figure 7 shows the changes of the objective function with T3 and T4 while the other parameters are constant and equal with values of mentioned in Table 1. It shows well that how the SMVS-DFT varies with their parameters. The SMVS-DFT is at minimum when T3 and T4 are equal according to computations.

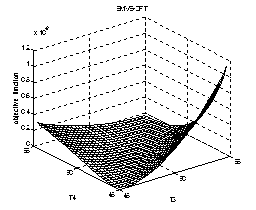Figure 7. The changes of the objective function with T2 and T4.

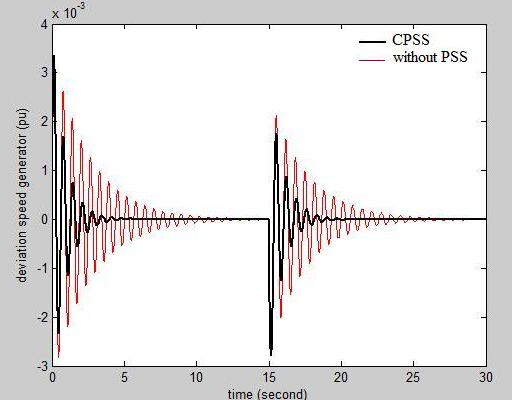Figure 8. Deviation speed of the generator in two states; without PSS and calculated parameters of the PSS by the CPSS.

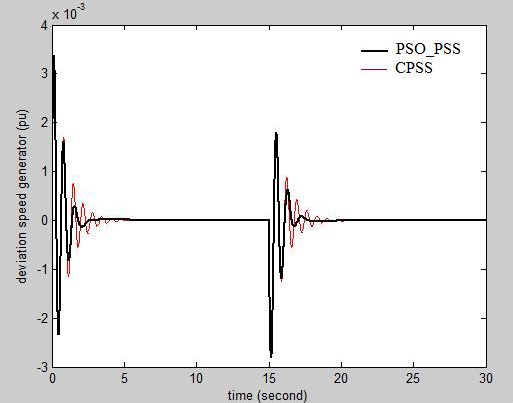Figure 9. Deviation speed of the generator in two states; tuned parameters of the PSS by the PSO and calculated parameters of the PSS by the CPSS.

6. Conclusions

Using a new objective function and algorithm of the optimization ICA and PSO, The optimal design of power system stabilizer can be done. The results of simulations show that new objective function, SMVS-DFT is a suitable objective function to study stability. This function decreases when the deviation speed of generator is damped. It is shown that and PSO algorithms have fast convergence to decrease SMVS-DFT and consequently to find PSS parameters and to damp disturbances. The evaluation of the comparison of the conventional PSS and the tuned PSS based on PSO and using SMVS-DFT depicts that the disturbances damping with PSO and using SMVS-DFT is better than CPSS. Also ICA using SMVS-DFT is better than PSO.

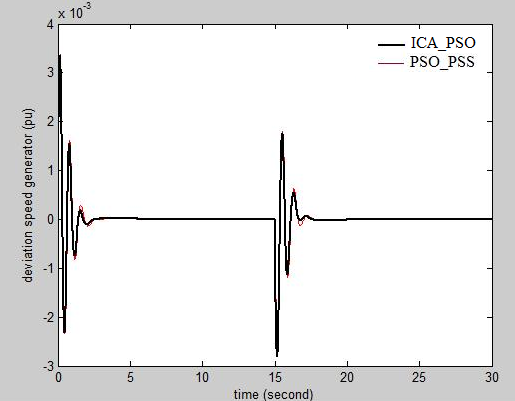Figure 10. Deviation speed of the generator in two states; tuned parameters of the PSS by the ICA and by the PSO.

Notes

¹SMVS-DFT