1. First of all, What is a Mathematical Machine?

A mathematical machine (related to the field of geometry) is an artifact designed and built for the following purpose, which does not depend on the practical use (if any): it aims at forcing a point, a line segment or a plane figure (supported by a material support that makes them visible and touchable) to move or to be transformed according to a mathematical law that has been determined by the designer [1].

The most well-known mathematical machine is the pair of compasses, to draw circles. It is the ancestor of many curve drawing devices and pantographs (Figure 1, on the left). Another class of mathematical machines is given by perspectographs (Figure 1, on the right) that are related to the roots of projective geometry and the tridimensional theory of conic sections.

Figure 1. Pantograph for rotation and Scheiner’s perspectograph (from [16])

Meantime, we have extended the definition of mathematical machines given above to those mechanical artifacts related to arithmetic. For instance, Figure 2 shows the pascaline Zero+1 [2, 3].

Figure 2. The arithmetical machine “pascaline Zero+1”

The use of working copies of historical instruments has the potential to address some important issues [4]: (i) Cultural: to make the users aware that mathematics is a developing part of human culture, connected with art, technology and everyday life; (ii) Affective: to foster a positive attitude towards mathematics, emphasizing the discovery and enjoyable aspects of mathematical activity; (iii) Cognitive: to foster the involvement of the body as a whole in mental processes, according to the most recent studies of both neuroscience and cognitive linguistics; and (iv) Didactic: to provide a suitable learning context in which activating important processes such as the construction of mathematical meanings and proof.

The activities with the mathematical machines are designed and carried out taking into account the elements mentioned above.

The mathematical machines are constructed starting from original sources, such as description in historical treatises. For instance, the perspectograph in Figure 1 (on the right) was presented by C. Scheiner in his “Pantographice seu ars delineandi” [5]. For this strong link with the history of mathematics, almost each machine is associated to a mathematician, who first constructed or described it (i.e., we tell about Scheiner’s perspectograph for Figure 1 on the right). In such a way, when a machine is proposed and described to students and public, the history of mathematics becomes a relevant part of the communication about machines and mathematics. This point contributes to the issue (ii) above.

This paper aims at presenting some activities involving the mathematical machines for teaching and learning mathematics and as means for its popularization. For the latter, we discuss those activities in the frame of lifelong learning and informal/formal learning.

2. “MMLab” and “Associazione Macchine Matematiche”

In this section, we present the people working with the machines in several kinds of activities.

2.1. Laboratory of Mathematical Machine (MMLab)

The Laboratory of Mathematical Machine [17] is a center for the research in mathematics education and popularization of mathematics. It belongs to the University of Modena and Reggio Emilia and is located in Modena. A certain number of mathematical machines (in particular, for geometrical transformation and conic sections) are hosted in an equipped room at the Department of Physics, Computer Sciences and Mathematics in Modena; other machines, mainly for perspective, are shown in another hall in the center of Modena. The principal components of the work carried out by MMLab are the idea of mathematics laboratory and the didactical research on the use of tools in teaching and learning mathematics. We can imagine the laboratory environment as a Renaissance workshop, in which the apprentices learn by doing, seeing, imitating, and communicating with each other and with the teacher. In laboratory activities, the construction of meanings is strictly bounded, on one hand, to the use of tools and, on the other, to the interactions between people working together. Over the years, several teaching experiments have been carried out in different Italian classes within the methodology of mathematics laboratory with mathematical machines [6]. The MMLab is also involved in projects for teacher education [7].

2.2. Associazione Macchine Matematiche (AMM)

Some high secondary school teachers in Modena formed the group that constitutes the heart of AMM at the beginning of the years '80. They were partially dissatisfied with results obtained with the methods of teaching followed during those years. They realized that sufficient attention was not devoted to the historical development of concepts and theories, with the risk of passing students with an inadequate picture of mathematics. They also observed a marginal role of the manipulation of instruments, which nevertheless had a relevant place in mathematics history. So they started with the historical research, the construction of the mathematical machines and the introduction of those instruments in their teaching practice. This involves the “discovery” of its mathematical properties and their theoretical justification. The Association builds the machines for the MMLab, as well as for others institutions (in Italy and abroad), and has in charge their preservation. It also collaborates with the MMLab for the organization of the laboratory sessions for students in MMLab rooms, participates in teacher education programs and organization of public exhibitions. On the website of AMM [16], several resources are available: catalogs of exhibitions, historical sources, simulations of the machines by different software (Dynamic Geometry Software, Cinema4d, Java).

3. The Activities with the Mathematical Machines

The mathematical machines are used in several kinds of activity. We first outline them in this section, while we propose some elements of their analysis in terms of informal, non-formal and formal education for discussion in the next section.

3.1. Exhibitions in Modena and Abroad

Since the beginning, the mathematical machines were used not only with students in classes, but they were showed in public exhibitions, in Modena, and in other towns (44 exhibitions, among them two in Maubeuge-FR). These exhibitions aim to illustrate both mathematical ideas and some methodology of teaching [8]. They are partially hands-on, in the sense that several instruments are usable for public (Figure 3, on the right), while the only animator can manipulate other ones.

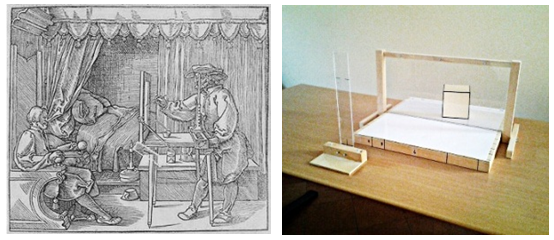Figure 3. Dürer’s glass: original drawing (Dürer, Underweysung der Messung 1525) and our copy (on the right)

The two big collections of the machines are Theatrum Machinarum and Perspectiva Artificialis. Due to the high number of models, small thematic collections are proposed for exhibitions. In general, in every exhibition, a choice has to be made between focusing on a particular topic and exploring a lot of mathematical ideas. We chose the first one, with the aim of allowing accessible the exhibition to student classes and offering the opportunity of discussing on almost all the machines. These collections are accompanied by poster and digital catalogs, all available in the AMM’s website [16]:

- Geometria a tu per tu (“Face-to-face Geometry”), proposed to several secondary schools in the Emilia-Romagna region; it contains models for illustrating geometrical transformations, curve drawers, Dürer’s perspectographs (see Figure 3).

- Apparenza e realtà (“Appearance and reality”) and L’occhio e la mano: antiche strumenti per la prospettiva (“The eye and the hand: ancient instruments for perspective”) focus on perspective; in particular, the latter contains some instruments described by J. Barozzi and G. Troili¹, who was born in a small town near Modena.

- Le coniche (“Conic sections”) and Rette e coniche (“Straight lines and conics sections”) on the theory of conics and relationships between conic sections and straight line.

- Geometria tra le mani (“Geometry on the fingers”) with mathematical machines especially constructed for haptic exploration in collaboration with the Institute for blind people “Garibaldi” in Reggio Emilia [9].

A permanent exhibition on perspective is available in Modena; it is open during public events such as the European researchers’ night (on September), within the network of university museums. Otherwise, it is available for visits by classes and mathematics laboratory sessions under reservation.

3.2. Exhibition and Students’ Involvement

In the edition of Perspectiva Artificialis in Cremona (2008), the exhibition was accompanied by workshops, whose organization involved some secondary school students. They first studied some mathematical machines (for instance, Figure 4, on the left) after school time; then they reproduced them (cf. Figure 4, on the right) under the guidance of their mathematics and arts teachers.

Figure 4. Jacob’s stick2 in [11], instrument constructed by the students (from [18])

With those instruments, they planned some laboratory sessions for the visitors of the exhibition (cf. Figure 5). In the report ([10], p. 377), the students write:

The laboratory became more significant for us because we are students who have to explain a mathematical content to non-expert people: the situation was overturned with respect to our usual situation; we were not in front of the teacher’ chair, but behind. We had to adopt a new form of communication: indeed, it was not the matter of showing that we had studied the lesson, but we had to give the opportunity of learning to other people. [...] The effort was not asked to the listener, rather than to us, who as guides had to involve the other people, changing our approach from time to time and the level of mathematical explanation.

Figure 5. Laboratory session within the exhibition (from [18])

3.3. Mathematics Laboratory Sessions for Students, Outside and Inside the Classroom

In the equipped rooms, we propose laboratory sessions to secondary school classes and groups of university students.

The topics proposed for those sessions are: (i) conic sections and conics drawers, (ii) geometrical transformations and (iii) perspective. Each session takes approximately two hours and covers three steps. For conic sections and geometrical transformations, the first step is an introduction, with the aim of situating the mathematical concepts that are going to be presented in the historical context of mathematics development (for instance, the Greek theory of conic sections is presented by models of cones with tightened thread). The second step of the session corresponds to an actual work with the mathematical machines in small group. As a class (usually) comes only once to the MMLab for a specific topic, the instruments given to the small groups are different from each other. Only in the session on perspective, all the students work with Dürer’s glass (Figure 3, on the right) and Barozzi’s instrument (Figure 6). In this step, students are guided by a worksheet: they manipulate and explore the machine, formulate conjectures and argumentations. In the third step, each group presents the characteristics of the explored machine. During this sharing stage of the laboratory, the mentor has the task of organizing the work carried out by the groups and establishing a link among the various mathematical machines presented, also placing them in their historical context.

For perspective, the session is always composed of three steps, whose content is a bit different from the other sessions described above.

- Observing some objects represented by the Dürer’s glass (see Figure 3, on the right), the students are introduced to the question of perspective representation (i.e., representing the 3D space into a 2D space – the paper).

- The students, split into groups and with a worksheet, draw specific images on copies of Dürer’s glass (Figure 3): they first use the ocular, then a small laser. In such a way, they are supposed to identify relevant properties useful in the justification of the rules for drawing the images of points or geometrical figures (cf. Figure 7). After this moment, the students use Barozzi’s plan perspectograph (Figure 6) for drawing the perspective of a solid (i.e., a cube). Compared to glass, this second instrument works exclusively on the plan: the images are obtained with operations only performed on the plan. In this task, the students have to trace the minimum of straight line and use the principal point and the points of distance.

- Guided visit to the exhibition on perspective. In particular, the students see:

- Some perspectographs are interesting for the development of the rules of the perspective drawing.

- Models showing some questions related to the perspective (i.e., different objects with same perspective image) and the relationships between perspective and shadows.

- Models showing different kinds of anamorphosis.

Figure 6. Barozzi’s instrument (with Dürer’s glass over it)

Figure 7. Dürer’s glass with the images of straight lines and points of distance

3.4. Stand in Popularization Events

The contact with foreign colleagues, above all French ones, fosters us to test another way for showing and working with mathematical machines. It concerns the preparation of a stand in large popularization events addressed to students and society. We participated to the “Salon des Jeux et de la Culture Mathématique” in Paris (2004), to “Fête de la Science” in La Réunion (2008) and the “MATh.en.JEANS Congress” in Lyon (2014).

In that kind of activity, the two major challenges for us were:

(1) to manage the exploration of the machines with the aims to give some mathematical insight with respect to the time that the visitor accepts of staying at the stand, without only proposing a short guided visit of the machines or a simple manipulation of them (corresponding to the question: “What do I do here?”);

(2) to manage the variety of visitors and their mathematical knowledge, coherently with the aim of offering not only manipulation or the description of the machine and its functioning.

4. Discussion

As this presentation shows, the mathematical machines are the same in the different activities. It is different the context, as well as the public, the form of communication, even if we have the finality of supporting and fostering mathematics learning.

From our perspective of mathematics education researchers, we want to try to characterize our action. In [12], we proposed the analysis of the relationships between users and machines, starting from the research about Lifelong learning. At the base of that work, there is the distinction among informal learning, non-formal learning, and formal education.

UNESCO ([13], p.8) considers these definitions in its report:

Formal learning takes place in education and training institutions, is recognized by relevant national authorities and leads to diplomas and qualifications. Formal learning is structured according to educational arrangements such as curricula, qualifications and teaching-learning requirements.

Non-formal learning is learning that has been acquired in addition or alternatively to formal learning. In some cases, it is also structured according to educational and training arrangements, but more flexible. […] It usually takes place in community-based settings, the workplace and through the activities of civil society organizations.

Informal learning is learning that occurs in daily life, in the family, in the workplace, in communities and through interests and activities of individuals. […] In some cases, the term experiential learning is used to refer to informal learning that focuses on learning from experience.

In the productive discussion on this topic ([14], [15]), relevant aspects to take into account are:

- There is not a large consensus about the definition of non-formal with respect to the other ones.

- Non-formal learning pays attention to the intention of the subjects to learn; this is a feature shared with formal learning. Indeed, both forms of learning can be treated as learning with a ‘participant orientation’: in particular, formal learning is intentional from both the learner’s and the institutions perspectives, while non-formal learning is intentional from the learner’s perspective.

- Non-formal learning can be structured in terms of learning objectives, time and support.

- Informal learning may be intentional, but it is largely unconscious: the subject is not aware that he is learning something. It is not structured.

Following some authors that formal, non-formal and informal learning do not have to be seen as discrete categories, but rather as elements within a “learning continuum”. Other researchers, as Rogers [14] proposes the metaphor of the iceberg, in which the emerged part corresponds to formal and conscious, while the invisible part corresponds to the other two. UNESCO highlights the importance of all the forms of learning and work in the direction of recognizing them, above all informal and non-formal learning [15].

Maschietto and Martignone [12] proposed to place three MMLab activities (guided visit for classes, MMLab laboratory session and classroom laboratory) in the continuum informal/non-formal, by the identification of six variables (structure, time, exploration, pupils’ involvement, teacher’s role, pupils’ position). In particular, guided visit of class to an exhibition is considered related to non-formal learning, laboratory classroom session is in the formal pole with some non-formal aspects. The authors characterize MMLab sessions as “laboratory education”, between non-formal and formal poles. With respect to this first work, other actions have been developed: groups of students working on mathematical machines hors school time (in the tradition of Emma Castelnuovo) and guides to exhibitions. For the latter, we have always asked to prevent guided visit to our exhibition, and in particular, we proposed training for them, but the experience of Cremona pays attention strongly on the kind of learning occurring in that activities from the three points of view of student, guide and public.

We think that it could be useful to have this regard to our actual activities, in order to identify which aspects can distinguish one from another one, and which kind of activities we could propose in this continuum. Moreover, these distinctions seem to be important in practical terms to balance between formal and informal learning [14]. If we were to take even the iceberg metaphor, we might ask if and how the non-formal and informal aspects are important for formal learning of mathematics. With this in mind, we could ask what can be done for the popularization of mathematics to reinforce this base.

Notes

1. https://archive.org/details/paradossiperprat00troi. Last Access 07/20/2017.

2. http://archiviomacmat.unimore.it/PAWeb/Sito/Inglese/PDF/221i.pdf Last Access 07/20/2017.