1. Introduction

Mankind has always constructed and used tools to accomplish tasks. Their importance has long been recognized at historical, psychological and cognitive levels. For example, the history of mathematics shows the use of tools to make calculations and to solve problems, but also to ground mathematics, as the tools for perspective drawings in regard to projective geometry[2]. In psychological and cognitive levels, Vygotskij[22] highlights that in the practical sphere the use of artifacts allows people to attain achievements that would otherwise have remained out of reach. He also distinguishes the function of mediation of technical tools and psychological tools (signs), whose use leads humans to a specific structure of behavior that breaks away from biological development and creates new forms of a culturally-based psychological process. Norman[15] uses the terms “cognitive artifact” to stress the role that any instrument, both material and symbolic ones, can play in fostering user’s cognitive potential.

Several research projects in mathematics education deal with the introduction and integration of tools in teaching and learning, at any school level. In this paper, we pay attention to physical reconstructions of tools drawn from the history of mathematics[4]. In particular, we consider the arithmetical machine Zero+1 (Figure 1), named “pascaline” by students who used it. We indifferently use the two nouns in this paper.

The history of mathematics education reports discussions about the use of tools, which was often related to a way of teaching mathematics contrasting with a frontal lecture[2].

In this paper, the use of tools in mathematics education is related to the methodology of “mathematics laboratory”[1]. In the laboratory activities, the construction of mathematical meanings is strictly bound to the use of tools on one hand, and to the interactions between people working together on the other hand. It is considered as a Renaissance workshop where the teacher plays the crucial role of expert-guide.

The topic of mathematics education with tools can be dealt from a double perspective, within mathematics laboratory: from the perspective of students that have to use a new tool to accomplish specific tasks on one hand; from the perspective of teacher that manages mathematical activities with tools on the other hand. This paper focuses on how the students can relate the use of a new tool to other tools already used. In particular, we analyze how students use tools within the perspective of “systems of instruments” [18], which are built from the set of all the means available for the subject according to proposed tasks and contexts. For this purpose, three teaching experiments with the pascaline are considered.

The paper is composed of six sections. In Section 2, the theoretical background is presented, while Section 3 contains our research questions. The methodology of the research is presented in Section 4 and the arithmetical machine Zero+1 in Section 5. The teaching experiments are analyzed in Section 6. The conclusion ends the paper.

2. Theoretical background

The teaching experiments considered in this paper are carried out within mathematics laboratory methodology[14], based on the theoretical frameworks of the instrumental approach and the theory of semiotic mediation. These frameworks are briefly presented below.

2.1. Instrumental Approach

The instrumental approach[19] is founded on the distinction between artifact (i.e., a material or abstract object, already produced by human activity) and instrument (i.e., a mix of the artifact and utilization schemes). Schemes are considered as “stable and structured elements in the user’s activities and actions” ([19], p. 65). Following[21], they are related to knowledge, often in an implicit way. During time and through specific tasks, an instrument to accomplish a class of tasks is formed by the subject. The process leading to the construction of instruments is called instrumental genesis. It is composed of two processes: instrumentalization and instrumentation. The former concerns the emergence and evolution of artifact components of the instrument; the latter points out the emergence and evolution of utilization schemes. Utilization schemes have both a private and a social dimension: the private dimension is specific to each individual, while the social dimension (shared by many members of a social group) results from the development of schemes during a process involving individuals who are not isolated[6].

From an educational point of view, the instrumental approach pays attention to students that have to perform complex cognitive processes when an artifact is proposed for solving mathematical tasks. In such a way, it highlights the relevance of supporting students’ instrumental genesis in the activities with tools. On the other hand, it suggests that an artifact can be a component of several instruments, depending on the kinds of task to solve and subject’s utilization schemes. But that is not all. A new instrument can meet other instruments previously constructed by the students[21], in class activities but also in extracurricular activities. Rabardel[19] stresses the relevance to take into account also the constitution of systems of instrument in an educational perspective. This paper intends contributing to the study of systems of instruments in learning mathematics.

2.2. Theory of Semiotic Mediation

The theory of semiotic mediation has been elaborated and applied to mathematics education by Bartolini Bussi and Mariotti[3]. It concerns the mediation of cultural artifacts to construct mathematical meanings, from a post-Vygotskian perspective.

According to this framework, in our teaching experiments the teachers used the pascaline as a tool of semiotic mediation, i.e., it is intentionally used to mediatemathematical contents through a designed didactical intervention. The mediation is a complex process ([11]) that implies the identification of an object to be mediated (mathematical content), the people subjected to mediation (students), a mediator (teachers), and circumstances (tasks on artifacts and mathematics laboratory). A key idea of this theoretical framework[3] is that tasks with artifacts foster a rich semiotic activity that produces signs, some of them are related to mathematical meanings that are objects of the mediation. The teacher constructs the tasks with tools and guides the evolution from the signs produced in the activities with artifact to mathematical signs (signs that are recognized as mathematical ones by the teacher as expert). The didactical structure supporting that evolution is represented by the didactical cycle. It is composed of activities with the artifact usually in small group, individual activities and collective mathematical discussions.

In this framework, the choice of an artifact to mediate a specific mathematical meaning is based on the study of its semiotic potential, defined as follows: “the double semiotic link which may occur between an artifact, and the personal meanings emerging from its use to accomplish a task, and at the same time the mathematical meanings evoked by its use and recognizable as mathematics by an expert.” ([3], p.754). The semiotic potential of Zero+1 is presented in Section 5.

With respect to a specific mathematical content, different artifacts can be available. The idea to connect them is suggested in[3] and further developed in terms of network of artifacts. Bartolini Bussi and Maschietto[5] discuss the idea of network of artifacts for place value. For the authors, this notion means that “no individual artefact is sufficient to form the meaning of place value notation to the extent of constructing the arithmetic operations and algorithms; rather it is the very system of them that can form this meaning in the plane of user’s consciousness, together with the awareness of the different features of each artefact.” ([5], p.193). In general, when the artifacts are analyzed, it is possible to stress similarities and differences among them, with respect to their structure, the embedded mathematical meanings, and utilization schemes. In other terms, they are analyzed and compared with respect to their semiotic potentials. In the quoted definition of network we identify two points of view: a teacher point of view and an user/student point of view. From the former, the aim of having a network of artifact corresponds to the potentiality to have a – limited – number of artifacts for a certain mathematical content and to propose their uses for allowing student to meet different meanings. The role of the teacher is relevant, even if in an implicit way. In fact, the teacher chooses the kind of artifacts for her/his students. The latter needs further analysis with respect to user’s awareness and different artifacts proposed by the teacher.

3. Research Questions

The use of different artifacts in teaching mathematics brings up for discussion their relationships and didactical potentiality on one hand, their appropriation by the students on the other hand. The notion of network of artifacts contributes to the former argument by the analysis of semiotic potentials of artifacts, but the impact of such a network on students’ learning needs to be more studied.

From students’ point of view, the introduction of an artifact solicits processes of instrumental genesis. According to the instrumental approach, an instrument is formed to solve a specific task. When different artifacts are proposed following a network of artifacts, questions aboutrelationships among different instruments and between systems of instruments and network of artifacts arise. Supposing that at least an instrument is formed with respect to a set of tasks on a specific mathematical content, the first research question is: how is a new instrument related to other instruments previously formed by students? If we take the assumption that a teacher knows relationships among the artifacts of a network when he/she introduces one of them to his/her students, a second research question is: how does he/she support the construction of systems of instruments for those students?

In this paper, we consider the network of artifacts related to the contents of place value and arithmetical operations, presented in[5]. It includes counting sticks and spike abacus (analyzed in[3]), and the pascaline. It will be discussed in Section 5. By the analysis of three teaching experiments carried out with the pascaline, we aim at contributing to answers to questions above.

4. Methodology

In this paper, the study of the network of artifacts presented in[5] is deepened by the analysis of the semiotic potential of the pascaline (see § 5.2).

The research questions are tackled on data from teaching experiments with Zero+1. Specifically, we consider:

A) A teaching experiment at grade 5 ([7],[8]);

B) A teaching experiment carried out from grade 3 to grade 4 on arithmetical operation ([12],[13]);

C) A teaching experiment at grade 6.

These teaching experiments refer to the mathematics laboratory (§ 2). These experiments were planned by the teachers of the classes working with the researcher. Each experiment was organized in didactical cycles, starting with group work on the discovery of the pascaline (i.e., how it is made, its functioning). The first activities aim at supporting students’ instrumental genesis.

The analysis is based on the videotapes of group work and collective discussions, on students’ worksheets and transcriptions of collective discussions.

5. The Arithmetical Machine “Zero+1”

5.1. The Structure of the Pascaline

The analysis of the structure of the artifact corresponds to answer to the question how it is made (if we consider the use of the machine, this kind of analysis corresponds to a first component of instrumentalization, § 2.1).

The machine Zero+1 (Figure 1) is a small plastic tool (27 cm x 16 cm), that evokes the world of numbers for the presences of numerals on three wheels.

The pascaline is composed of a base with a gear train (five wheels): three yellow wheels (A, B and C, Figure 1 on the right) at the bottom and two orange wheels (E and D, Figure 1 on the right) at the top. Each wheel has ten teeth; the Arabic numerals are written on each tooth of each yellow wheel, while a purple arrow is integral with each orange wheel. Below wheels A, B and C, small red pyramidal prisms (“small triangles”) indicate a tooth; there is a movable point down on the right, which can be put in the holes between the red triangles. The wheels can move clockwise or anticlockwise; wheels A, B and C are not directly engaged. For each yellow wheel (A, B and C) there is a tooth-stop that forces a jerk movement, that is one-tooth rotation.

From the configuration (000) for the yellow wheels over the red triangles, wheel A can rotate clockwise until (009) without any other wheel moves. During the passage from 9 to 0 for wheel A (i.e., when wheel A has turned a complete rotation), wheel D makes wheel B go one step ahead (see Figure 1 on the right). For this rotation, the tool resists a bit more and requires a stronger push than that for the tooth before. This movement is accompanied with a thud sound. A similar situation occurs for the passage from (099) to (100): in this case, all the wheels move and the sound is louder. In so doing, D (like E) is an auxiliary wheel to transmit motion. This machine works as a counter in base ten (i.e., it is an adding machine).

This artifact is not a black box, in the sense that all its components are visible and touchable.

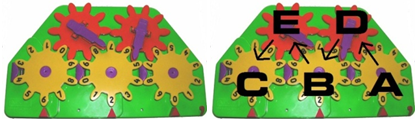Figure 1. The arithmetical machine Zero+1 (pascaline). It is produced and sold by the Italian company “Quercetti” (http://www.quercetti.it)

5.2. Semiotic Potential of the Pascaline

Bartolini Bussi & Mariotti[3] consider three elements for the study of the semiotic mediation of an artifact: 1) mathematical content, 2) historical and cultural dimensions, 3) utilization schemes constructed in order to accomplish a given task (or a set of tasks). In this kind of analysis, the links among the piece of mathematics knowledge, the artifact and the utilization schemes are considered. With respect to the last element, in this section the expression ‘ways of using’ will be used instead of ‘utilization schemes’ in order to stress the feature of the a priori analysis presented here. The latter expression will be reserved to the analysis of students’ activity in the teaching experiments.

5.2.1. Mathematical Content

The pascaline performs writing numbers and making the four elementary arithmetical operations.

Zero+1 allows three-digit numbers in a decimal positional notation to be represented: each tooth of the three yellow wheels (A, B and C) represents a digit. With respect to Figure 1 (on the right), wheels A, B and C represent units, tens and hundreds respectively.

The functioning of Zero+1 is consistent with the recursive approach to numbers. In Peano’s (1858-1932) axiomatic for arithmetic[17], the set of natural numbers is defined starting from three primitive terms (number, zero and successor function) and five postulates involving the three terms. The successor function corresponds to 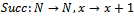. So, the sequence of natural numbers can be generated by iterating this function “+1” from the starting number zero. Addition and subtraction are defined in a recursive way.

5.2.2. Historical and Cultural Dimensions

Zero+1 is inspired by the mechanical calculators, like the Pascaline (Figure 2) designed by Blaise Pascal (1623-1662). They appeared in the XVII century to need people aiming to perform calculations quickly and without mistakes. Pascal’s Pascaline had been considered the first mechanical calculator until a correspondence between Wilhelm Schickard (1592-1635) and Johann Kepler (1571-1630) was discovered, in which the former described his calculator (1623) destroyed during a fire.

Figure 2. The pascaline by B.Pascal (1642)[16]

With respect to calculating tools used at that time, like the coin abacus, the Pascaline presented digits, in particular the zero, and implemented the place value notation in base ten. From an epistemological viewpoint, the presence of zero is a significant feature: in the abacus the zero indicates a lack of units at any level, while it has a function in the written system of numeration. It is a label in the Pascaline.

5.2.3. Ways of Using Zero+1

In the presentation of ways of using the pascaline (corresponding to answer how the machine works in to order to do a specific tasks), the relationships with the mathematical content (specified in § 5.2.1) are taken into account (corresponding to the question why the machine works in that way). In this way, one side of the double semiotic link characterizing the semiotic potential is described (§ 2.2). The other side is related to task accessible to students, according to educational aims.

The principle of functioning is the rotation of a tooth at a time, defined by the structure of the machine (§ 5.1). This is the basic action. According to the idea of mathematical machine, the pascaline can be used for counting, representing numbers in base ten and making arithmetical operations. For this kind of tasks, ways of using are studied.

A. Counting and Counting Back

Counting is realized by the iteration of the basic action pushing clockwise on wheel A (units wheel); counting back corresponds to an anticlockwise rotation. At the end, the number is read over the three teeth over the red triangles. In this way, the sequence of natural number is obtained by the iteration of the function Succ, according to Peano’s axiomatic (§ 5.2.1).

B. Representing Numbers

On the pascaline, natural numbers until 999 can be represented. Starting from the initial configuration (000) on the yellow wheels, ways of using are characterized as follows:

-[Way 1]: turning wheel A one-tooth clockwise as many times as the quantity given by the number (writing by iteration);

-[Way 2]: units, tens and hundreds are identified in the number; for each of them, writing by iteration is applied to wheels A, B and C respectively (writing by decomposition).

At the end of these actions, the number is read on the three teeth next to the red triangles (for instance, 620 in Figure 1). The starting point to represent the numbers (as well as to make calculations) corresponds to the configuration (000) over the red triangles. However, this condition raises a non-trivial question about representation, because numbers written with one or two 0-digits on the left has to be accepted. The two ways differ in knowledge on which they are based: [Way 2] requires the understanding of the decomposition of numbers in units, tens and hundreds, with respect to[Way 1]. From teaching point of view, this difference is important because it can suggest different tasks depending on students’ level.

Another way[Way 3] could be possible: writing by decomposition by the control of the digits over the red triangles. In this way, wheels are rotated until the digits of the number to represent appear over the corresponding red triangles. There is no need to put the initial configuration (000), even if the coherence of the final configuration has to be checked (for instance, if the representation of the number has two digits, wheel C has to corresponds to 0 over its red triangle). So, the users/students control the final configuration of the wheels rather than the process of turning wheels. If the value of each yellow wheel is not recognized, writing as (130) can be possible for the number 13 (instead of (013)).

C. Making Addition and Subtraction

Addition corresponds to the clockwise rotation of the yellow wheels, while subtraction to anticlockwise rotation. This structural difference strictly links the two operations (one operation is the inverse of the other one).

For instance, the addition 24+13 has to be made. Zero+1 has to be set up on the initial state (000), the first addend 24 is represented, and then two basic ways of completing the calculation can be executed:

-[Way 1] wheel A is turned 13 times one-tooth clockwise (addition by iteration); it corresponds to a counting on and so, to the definition of addition in Peano’s axiomatic (§ 5.2.1);

-[Way 2] the second addend 13 is separated into units and tens, each of them is added by the rotation of wheels A-units (3 times one-tooth clockwise) and B-tens respectively (1 time one-tooth clockwise) (addition by decomposition). In this way, the order of execution is not important: one can start from units, but also from tens (or hundreds, if any).

At the end, the result is read over the red triangles.

D. Making Multiplication and Division

Multiplication and division are made as repeated addition and subtraction, respectively. These operations need an external memory (i.e., paper and pencil, fingers) in order to count the number of repetitions (with a particular attention to the fact that the number of repetitions corresponds to the second factor minus one, i.e. 13×4 corresponds to write 13 and add 13 for 3 times). In that sense, the pascaline is not an automatic machine for multiplication and division.

The way of making division is coherent with the meaning of the Euclidean definition on natural numbers. Indeed, at the end of subsequent subtraction, the residual is read over the red triangles while the quotient has to be read from the external memory.

E. Comments

In conclusion, Zero+1 embeds the meanings of succession of natural numbers, unary operation, inverse operations, Euclidean division and place value notation in base ten.

Ways of using can become utilizations schemes for students when the pascaline is proposed with specific tasks. On the other hand, utilization schemes refer to a certain mathematical knowledge. So within the theory of semiotic mediation, the pascaline, can be used to mediate certain mathematical contents. According to the instrumental approach, utilization schemes can also evolve through the proposition of new tasks or constraints for already performed tasks. For instance, a study of utilization ways under the condition of the minimum number of basic action could be carried out.

5.3. Network of Artifacts

In[5], a network of artifacts for the place value for natural numbers is proposed: it is composed of counting sticks (dating back to ancient China, they are thin bamboo or plastic sticks, which are counted, grouped and bundled), spike abacus (it consists of 3 spikes and 27 beads or more; each spike represents a particular position of a digit and can have a maximum of 9 beads) and pascaline. In particular, spike abacus is analyzed in terms of semiotic potential in[3]. The mathematical meanings potentially attached to this network are[5]:

- One-to-one correspondence is in the foreground for the counting sticks and abaci;

- Grouping (groups of ten) is in the foreground for the counting sticks and abaci;

- Number symbols are written only on the pascaline;

- The generation of the written number sequence is in the foreground in the pascaline.

This network of artifacts can be also considered for arithmetical operations, above all addition and subtraction. The attached mathematical meanings are:

- Counting all is in the foreground for the counting sticks and abaci (meaning of binary operation);

- Counting on is fostered for the pascaline (meaning of unary operation);

- Addition and subtraction as inverse operations is in the foreground for the counting sticks and the pascaline;

- Results are only written in the pascaline;

In addition, the conventional order used in spike abacus (from right to left) and transposed in written algorithm for addition and subtraction does not need with the pascaline, because of the number to be carried out automatically. Furthermore, the two opposite movements for wheel highlight the idea of composition and decomposition of unit making operations. In the shift from counting sticks and abaci to written representations of numbers, the zero appears as a place holder, while in the pascaline it is rather a label, as stressed in § 5.2.2.

The above differences justify why it is not only better but necessary to refer to a network of artifacts rather than to one only artifact. Our research questions concerns the network from the point of view of students using the artifacts. In Section 6, they are discussed in relation with three teaching experiments carried out within the mathematics laboratory methodology.

6. From Teaching Experiments

In this section, the analysis of the teaching experiments can contribute to answer the two research questions (§ 3).

6.1. Systems of Instruments for Place Value

The first teaching experiment is carried out at grade 5 class, with the idea of mediating the meaning of positional notation in any base ([7],[8]). It is composed of two phases. The first phase consists of four sessions (Steps 1-4) and is intended to lead to the construction of the instrument pascaline to write numbers and make arithmetic operations in base ten[7]. The second phase consists of two sessions (Steps 5 and 6) on writing numbers in smaller bases than the base ten[8]. In particular, in Step 5, the task for the group work requires to imagine and/or build a pascaline for base five and to make some arithmetical operations. The task aims to foster a process of instrumentalization of the pascaline, bringing to a generalization of the place value meaning.

6.1.1. Existing Systems of Instruments

Since grade 1 class, the teacher has exploited a network of artifact to construct the meaning of place value in base ten, based on grouping and number representation by digits. She worked within the mathematics laboratory methodology (§2). In such a network, the artifacts were: the “counting-hand” (one hand is drawn on paper and then cropped, is then glued on a cardboard leaving the fingers free), spike abacus, number line, and grouping (“ten-bag”).

During the school years, the teacher was careful to foster the students to link different instruments. For instance, Figure 3 shows student’s representations of the utilization schemes to write numbers and to calculate by several instruments. In this section we do not analyze the construction of those instruments over the time, but we look for answer to our first research question concerning how a new instrument is related to other instruments by the students.

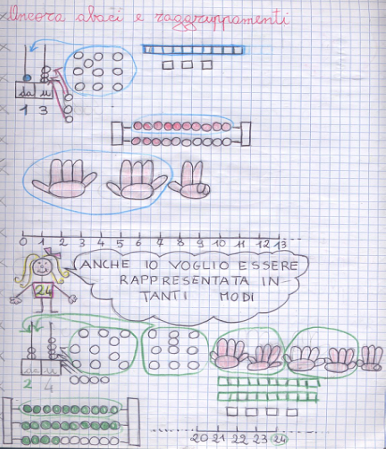Figure 3. Graphical representations of a system of artifacts[8]

Hereinafter, two examples from group work in Step 5 will be analyzed.

6.1.2. System of Instruments: the First Example

We consider the worksheet filled by three pupils during the group work. A Zero+1 for base five is correctly drawn (Figure 4). The students seem to call back a system of instruments and use it to show and control their resolution. The analysis of their worksheet consists of 3 parts.

1) The students consider the procedure for the number to be carried. That represents the fundamental element allowing the students to confirm the number of digits for the representation of number in base five.

Davide is right because grouping in base 5 you must have 5 digits, that is from 0 to 4; otherwise, if[it is from 0] to 5, then the change concerns base 6 and it is wrong.

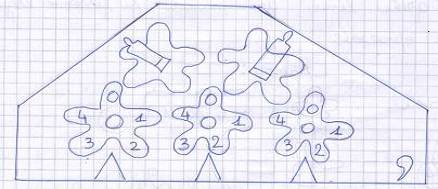Figure 4. Pascaline for base five[8]

2) In their text, the students refer to several instruments (Figure 6), having as artifact components some elements of the network (§ 5.3). The text contains not only several signs shared in the class during previous activity (§ 6.1.1), but also their transformations according to the tasks to accomplish. For instance, the expression “ten-bag” is adapted in “five-bag” (“sacchetto cinquina” in Figure 5). That linguistic transformation is accompanied by the corresponding representation of the bag (Figure 5).

Let's represent a graphical schema to understand 1 and 2 in base 5, as we made in grade class 2.

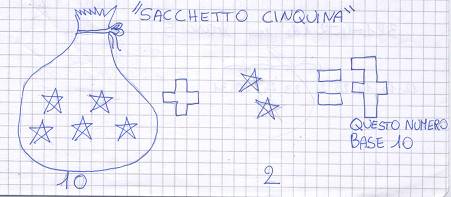Figure 5. Five-bag

The number line is also constructed for base five (Figure 6, at the top) and proposed to make additions and subtractions.

Figure 6. System of instruments

On the other hand, calculating through the number line is consistent with the recursive approach evoked by Zero+1.

3) The third moment starts with an intervention of the teacher proposing to make two operations (11+14 and 23–14) by the new arithmetical machine. The pupils recall two different procedures, in which they refer to the machine and to the number to be carried.

This first example seems to show the integration of an instrument in a system occurs through the representations of those instruments. These representations contains artifact components but also parts of utilization schemes.

6.1.3. A New Instrument: the Abacus-pascaline

We consider two excerpts of the text written by other pupils during the group work. The first excerpt seems to show a generalization process, grounded in searching invariant elements between the pascaline for base ten and the required pascaline for base five (e.g., the number to be carried). The second excerpt corresponds to a part of the group work occurring after a teacher’s intervention; it contains an interesting graphical representation involving several artifact components of instruments constructed by the pupils.

1) At the beginning, the pupils write as follows:

To construct a pascaline for base five, I have to construct some gears starting from 0 to 0 4. If you imagine that 9[for base ten] is as 4[for base five], you also imagine the number to be carried that goes to ten. This way is also valid for tens wheel, and so on for all the positions.

2) ATTENTION

If we think in base 5, we have to think that we do not read twelve[if the written number is 12], but that we read in base 5, that is two remains two[units], ten[that is the digit 1, tens place] must become 5, now we have to sum the result, that is 7[...]

This excerpt presents two traces of a generalization process for the meaning of place value:

- The digit 0 is cancelled and replaced by the digit 4. The reference to the digit 0 seems to evoke the interaction with the material tool, when a turn is completed by turning the wheel until 0 is over the red triangle. Instead, stopping at 4 is coherent with the polynomial representation of numbers in the specific base of this task.

- The words “ten” and “five” (point 2 in pupils’ text) evoke the size of grouping.

There, the pupils seem to distinguish between the quantity expressed by words and the symbolic representations in a positional notation, with reference to different basis.

2) After the teacher has recalled their past experience, in the graphical register the pupils create a new instrument, a kind of hybrid mix of abacus and pascaline.

[The teacher asks and writes on the paper, Figure 7 at the top] When at grade 1 I taught tens, which representations and instruments did we use?

[The teacher asks and writes on the paper; Figure 7 at the bottom, to the right] Why[have you drawn] five small squares upon each bar? Are they useful?

[The pupils write on the paper] Because we have imagined that a small square corresponds to 0, after I arrive until 4 and then a five-number goes up; otherwise we can draw 4 small squares and then we imagine the 0 because 0 is a void position.

In the new instrument, the following elements are detected:

- The bars (artifact components) are “five-number-bars” (in an analogous way the pupils worked in base ten): each bar is divided into five squares, which are counted and labeled 0, 1, 2, 3 e 4. These bars can be considered as the bar of the abacus, while the digits come from the Zero+1;

- The signs under the digits on the bars seem to recall the teeth of the Zero+1; they can be considered as artifact components;

- The linguistic expressions “units”, “five-numbers” and “five-numbers—five-numbers” (written at the base of the abacus, see Figure 7) highlight the role of the abacus as instrument of reference. These expressions are mainly related to the mathematical meaning embedded in the instrument.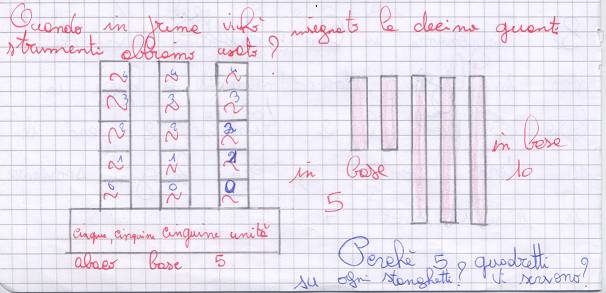

Figure 7. Drawing 3 in students’ worksheet

In the graphical register, the pupils construct a new artifact merging elements from other instruments (i.e., from their artifact components). Even if students do not write how it can be used, this representation can be interpreted for representing the relationships between different instruments, related to the same mathematical content.

This excerpt shows an instrument whose artifact component does not belong to the network of artifacts proposed by the teacher (§ 6.1.1). With respect to our first research question, this suggests that a system of instruments is grounded not only on schemes, but also in representations of the artifact components. For the second research questions, the role of the teacher analyzed is stressed: she recalls previous experiences concerning the network of artifacts.

6.2. Meeting Between Zero+1 and Other Instruments for Arithmetical Operations

The second teaching experiment ([12],[13]) was composed of nine steps and was carried out at the end of grade class 3 (Steps 1-4) and at the beginning of grade class 4 (Steps 5-9). When the experiment started, the students knew the four arithmetical operations and the procedures to make calculation. The contents of mediation were: 1) recursive principle to construct numbers and do operations, related to the meaning of unary operation; 2) meaning of algorithm for arithmetical operations (addition and subtraction). In this paper, the analysis of Step 3 is considered. In that step, additions are collectively made, for a social construction of utilization schemes.

During the mathematical discussion at the end of Step 3, the students spontaneously refer to spike abacus and pocket calculator. The abacus was introduced in the classroom for place value[9] and after it was used for operations the year before. The pocket calculator instead does not yet belong to students’ school experience, but to their extracurricular experiences. The calculator is not an artifact of the network for the teacher, but it is already an instrument for some students. This collective discussion can be interpreted as the emergence of students’ systems of instruments partially constructed during the classroom activity (abacus), partially independently constructed (calculator). This system seems to appear when the instrument pascaline is formed for the students (i.e., utilisation schemes are more or less stable to solve specific tasks). On the other hand, the teacher takes into account students’ instruments and solicits the emergence of the characteristics (Table 1) of those instruments by a collective discussion. Table 1 shows that the students compare and sometimes contrast the two instruments (calculator and pascaline) with respect to artifact components (#2, #6), utilization schemes (#2, #3, #5) and mathematical content (#1) Some interventions (for instance, #4) highlight an epistemic value of utilization schemes.

Table 1. Comparison Zero+1/pocket calculator Speech Comparison (students’ intervention during the discussion) Contents #1 Tom When you use the pascaline you must think, instead when you use the pocket calculator you just have to write the operation and it makes the calculation. Operations #2 Marco The calculators have buttons, all go fast, have electricity and gives you the result, while with the pascaline you have to do everything by hand and turn until you do not make the result. Structure and some utilization schemes (push the button and turning) #3 Federico The calculator has only one way to be used, instead the pascaline does not have a precise way: you can act from right to left or from left to right. Utilization schemes #4Lorenzo In the calculator, the number to be carried is not written, but it calculates it automatically, instead in the pascaline the small arrow makes the change more visible, so it makes you think and understand. Embedded knowledge in the artifacts #5 Laura With the pascaline, you need to take longer to make operations with respect to the calculator. Performance related to utilization schemes #6 Chiara P On the pascaline there is a comma, while on the calculator there is the point that replaces the comma. Signs presented by the artifact

With respect to the second research question, the analysis of this excerpt seems to confirm the results of the first teaching experiment: the teacher fosters students’ personal instruments to emerge within a social construction of systems of instruments. Teacher’s didactical actioncontinues after the end of this teaching experiment, as the teacher reviews these elements relating to systems of instruments tools and supports the instrumental genesis of the instrument pocket calculator[10].

6.3. On the principle of economy

The third teaching experiment involves a grade 6 class (it corresponds to the first year of secondary school in Italy, 11-12 years old students) and is composed of four steps. The pascaline is introduced as a calculator, even if it is proposed to mediate processes as conjectures and argumentation in arithmetic, rather than mathematical contents as in the teaching experiments analyzed in the previous sections.

After the first group work for exploring Zero+1, the spike abacus is recalled by the pupils during the collective discussions in terms of the first non digital instrument used at primary school. The comparison between the two instruments, spike abacus and pascaline, takes into account their utilization schemes. For some students, the abacus and Zero+1 are two equivalent instruments because “they make the same thing”, other students remark the advantage of using Zero+1 with respect to the spike abacus to make addition and subtraction. In so doing, the students compare the set of tasks in which they can use the two instruments. For them, there is no advantage with the pascaline. This is a position contrary to the idea of system of instruments. But the teacher leads the pupils to propose arguments for supporting the position “to make the same thing”, and so to explicit utilization schemes for abacus. During this kind of discussion, it emerges the abacus is used to make operations with numbers minor than twenty (the set of tasks). At that moment, the teacher introduces a kind of distance between the two instruments when she proposes to make the operation 237+398 and asks to choose the most suitable instrument for that task. This task allows students to compare Zero+1 and abacus thought their utilization schemes following a kind of principle of economy concerning the number of actions to do. When the students can make the addition with the two instruments, it is evident for almost all of them the advantage of using Zero+1, first of all because of the number to be carried in an automatic way. Finally, the teacher proposes to fill a table with differences and similarities. The former considers some artifact components and the manipulation of the artifacts (i.e., automatic movement for the number to be carried). The latter focuses on mathematical content. However, the set of tasks or utilization schemes are not written in the table.

This third example reinforces the role of the teacher in taking into account the construction of instruments and systems by the students. The link between instruments is made from the comparison of the corresponding utilization schemes, as in the second teaching experiment analyzed in this paper. The differences are useful in order to characterize the two instruments and their instrumental distance.

7. Conclusions

This paper aims to investigate the notion of system of instruments, from student’s point of view, starting from the notion of network of artifacts. It is an exploratory study based on the analysis of three teaching experiments, in which an arithmetical machine for writing numbers and making operations is introduced at different school levels. We have not considered the whole teaching experiments, but we have focused on when other instruments are recalled by the students and linked (if any) to the pascaline.

The analysis suggests two levels of instrumental geneses. At a first level, students’ instrumental geneses concern the only pascaline. At a second level, instrumental geneses involve the new instrument pascaline and the other instruments already constructed by the students. Links can be established with respect to the mathematical contents at a first moment, as it can be obvious to expect. But more relevant links are related to artifact components and utilization schemes, for a set of tasks. Moreover, it seems to be important the existence of a certain “distance” among instruments (an instrumental distance), not only among their artifact components but also in terms of epistemic value of using the pascaline. For instance, specific tasks can allow some mathematical meanings to be reformulated or recalled and better understood. This is the case of changing base in writing numbers: the pupils clearly distinguish among numeric quantity (in the bag), numeral and place value notation. These elements seem to be important in order that the students form their system of instrument. On the other hand, systems of instruments can be constructed by the creation of new instruments in graphical register, as a hybrid entity from previous instruments. In such a way, their artifact components do not belong to a network of artifacts on the target mathematical content. With respect to the second research question, the analysis seems to stress the importance of the teacher in supporting the constitution of systems of instruments by the means of specific tasks or by collective discussion in which students’ instruments emerge. Finally, it seems to be relevant to maintain the distinction between network of artifacts from the teacher’s point of view and system of instruments from the student’s point of view: the latter can be richer than the former. For instance, pupils can create new instruments. But this point needs further investigations on the cognitive process of creating new instruments. But the definition of a network of artifacts could be mirrored in an instrumental distance for the students.

ACKNOWLEDGEMENTS

I wish to sincerely thank the teachers R. Canalini, A. Casarini, F. Clementi. F. Ferri and V. Pradelli.