-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Economics
p-ISSN: 2166-4951 e-ISSN: 2166-496X
2021; 11(4): 107-113
doi:10.5923/j.economics.20211104.01
Received: Sep. 19, 2021; Accepted: Oct. 12, 2021; Published: Oct. 30, 2021

Estimation of Trade Permeability Between Benin and Nigeria in a Land Borders Closure Case
Amour Gbaguidi Amoussou 1, Aristide Medenou 2, Moïse Lawin 3
1Institut de Mathématiques et de Sciences Physiques (IMSP), Université d’Abomey-Calavi, Cotonou, Benin
2Laboratoire de Recherche en Economie de Saint-Louis (Sénégal), Direction Générale de l’Economie (DGE), Ministère de l’Economie et des Finances, Cotonou, Benin
3Direction Générale de l’Economie, Ministère de l’Economie et des Finances, Cotonou, Benin
Correspondence to: Amour Gbaguidi Amoussou , Institut de Mathématiques et de Sciences Physiques (IMSP), Université d’Abomey-Calavi, Cotonou, Benin.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, we will construct some estimator of import permeability and export permeability. Based on the nonparametric approach, we will prove that these estimators are consistencies. We will first propose a kernel that meets the criteria of consistency of the multivariate regression function estimator. This kernel will be used to projected import and export values between Benin and Nigeria. Moreover, we will also prove that our nonparametric approach is more efficient than the multivariate linear regression model under the root means square error criteria.
Keywords: Nonparametric regression model, Import, Export, Impact analysis, Trade permeability
Cite this paper: Amour Gbaguidi Amoussou , Aristide Medenou , Moïse Lawin , Estimation of Trade Permeability Between Benin and Nigeria in a Land Borders Closure Case, American Journal of Economics, Vol. 11 No. 4, 2021, pp. 107-113. doi: 10.5923/j.economics.20211104.01.
Article Outline
1. Introduction
- Linear regression model is a linear approach for modelling the relationship between a scalar response and one or more explanatory variables. The case of one explanatory variable is called simple linear regression; for more than one, the model is called multivariate linear regression. Linear regression model was the first type of regression analysis to be studied rigorously and to be used extensively in practical application (e.g. [26]). For instance, in 1993, some authors (e.g. [1]) modelled imports and exports of France by respectively
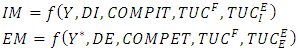 where IM the import demand, EM the export demand, Y the GDP in France, Y* the GDP abroad, COMPIT the competitiveness term of the imported product, COMPET the competitiveness term of the exported product, DI the domestic demand for manufactured goods, DE the foreign demand for manufactured goods,
where IM the import demand, EM the export demand, Y the GDP in France, Y* the GDP abroad, COMPIT the competitiveness term of the imported product, COMPET the competitiveness term of the exported product, DI the domestic demand for manufactured goods, DE the foreign demand for manufactured goods, 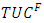 the rate of capacity utilization of France’s trading partners,
the rate of capacity utilization of France’s trading partners, 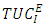 the capacity utilization rate of imports and
the capacity utilization rate of imports and 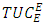 the capacity utilization rate of exports. These authors have given particular linear forms to the functions
the capacity utilization rate of exports. These authors have given particular linear forms to the functions 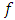 and
and 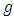 . Linear regression analysis depends on some assumptions. One of the most important is that the type of relationship between dependent and independent variable or variables is linear and parametric. Under such circumstances, in order to make better assumptions, we alternatively adopted a nonparametric approach.Nonparametric regression are statistical models, and the first meaning covers techniques that do not rely on data belonging to any particular parametric family of probability. It is a category of regression analysis in which the predictor does not take a predetermined form, but is constructed according to information derived from the data. In a multivariate case the asymptotic properties of the Nadaraya-Wastson kernel estimator [13] of an unknown regression function was established [9]. The authors have studied the asymptotic normality, consistency and uniform weak consistency of the estimator based on some assumption on the used kernel. Benin and Nigeria share more than 800 km of borders where different populations whose ethnology is very similar have historically settled [24]. Around these borders, both land and lagoon, are established several local markets, which build up the meeting points and exchange between urban and rural populations. Between these two countries (Benin and Nigeria), commercial exchanges concern a wide and diversified range of products and re-exported products which constitute the central element of economic relations between Benin and Nigeria. They are stimulated on the one hand by the existence of a higher level of taxation on imports in Nigeria, due to the Nigerian protectionist policy, and on the other hand by the poor reputation of the port of Lagos, in terms of delays and insecurity for goods [12]. Given the difficulties Nigerian importers face, they prefer transit to re-export, as only Nigerian customs duties should theoretically be paid. In August 2019, trade relations between Benin and Nigeria deteriorated to the point where Nigeria unilaterally closed its land borders to Benin. The reason cited that supports this closure is that, the goods re-exported by Benin to Nigeria are mainly from Europe or Asia. This closure is also based on theoretical reasons based on import substitution policies or theories of infant industries [7]. The, products re-exported from Benin to Nigeria at a relatively lower cost than local products, thus undermining the competitiveness of Nigerian companies. As a result, stricter controls have been introduced at the Nigerian borders to prevent goods from Benin from entering Nigeria. In similar contexts, the literature shows that strict controls at the border or at checkpoints can only limit the entry of unwanted products. This reflects the trade permeability notion. We define the permeability of a trade as indicator which determine the capacity of a country to followed import or export when the border is closed. Specifically, the import permeability between two countries is the share of imports when the borders are closed in the imports an open border case during a period and the export permeability between two countries is the share of exports in a closed border situation in the exports an open border case during a period. It is important to noted that the import values of Nigeria to Benin in 2019 are known and available on the ITC website https:www.intracen.org. This data takes into account the closure of the Nigerian border in 2019 which lasted four months. Our approach is to first estimate these import and export values if the border was not closed using the nonparametric model. After that, we can evaluate the different permeability over the whole year 2019 and over the four months of closure. Recently, the problem of the effects of the Nigeria land borders closure on Benin based has been investigated in a publication such as [3]. The authors have shown that the closure of Nigerian borders has a negative impact on the Benin economy with respect to its total exports based on some fundamental assumptions such as: The simulations were made taking into account the average trade trend between Benin and the rest of the world over the last two years. We believe that this assumption is too strong for the efficient of the projection because the share of imports and exports between Benin and Nigeria at the world level depends according to the previous assumption only on the average between led shares of 2017 and 2018. Moreover, the authors have not studied the concept of permeability of trade. Thus, we will remove this assumption and use data from 1977 to 2018 for the different projections with a nonparametric approach, and we will propose a consistence estimator of the permeability in land closure borders case. In this paper we will propose a multivariate kernel, which satisfied the consistency assumptions of nonparametric regression estimator developed in [9]. In other to substantiate our approach, we will prove that the nonparametric model is more efficient than the multivariate linear regression model under the root mean square error criteria. Using this proposed kernel, we will project the import value of Benin from Nigeria for the year 2019 an open border case. Moreover, the export value from Benin to Nigeria will be estimated for the same year 2019 an open borders case. Based on these trade estimators, we will propose a consistent result for our import and export permeability estimator. At the end, the estimation of the indicators (import and export values, import and export permeability) will be calculated and analyzed. In the following, we will give a literature review in section 2 on trade values. In section 3, we will develope the methodological tools on nonparametric kernel regression model and the modelling result of import and export. As an application, we will evaluate the permeability result of Benin for the year 2019 with a land Borders Closure case in section 4.
. Linear regression analysis depends on some assumptions. One of the most important is that the type of relationship between dependent and independent variable or variables is linear and parametric. Under such circumstances, in order to make better assumptions, we alternatively adopted a nonparametric approach.Nonparametric regression are statistical models, and the first meaning covers techniques that do not rely on data belonging to any particular parametric family of probability. It is a category of regression analysis in which the predictor does not take a predetermined form, but is constructed according to information derived from the data. In a multivariate case the asymptotic properties of the Nadaraya-Wastson kernel estimator [13] of an unknown regression function was established [9]. The authors have studied the asymptotic normality, consistency and uniform weak consistency of the estimator based on some assumption on the used kernel. Benin and Nigeria share more than 800 km of borders where different populations whose ethnology is very similar have historically settled [24]. Around these borders, both land and lagoon, are established several local markets, which build up the meeting points and exchange between urban and rural populations. Between these two countries (Benin and Nigeria), commercial exchanges concern a wide and diversified range of products and re-exported products which constitute the central element of economic relations between Benin and Nigeria. They are stimulated on the one hand by the existence of a higher level of taxation on imports in Nigeria, due to the Nigerian protectionist policy, and on the other hand by the poor reputation of the port of Lagos, in terms of delays and insecurity for goods [12]. Given the difficulties Nigerian importers face, they prefer transit to re-export, as only Nigerian customs duties should theoretically be paid. In August 2019, trade relations between Benin and Nigeria deteriorated to the point where Nigeria unilaterally closed its land borders to Benin. The reason cited that supports this closure is that, the goods re-exported by Benin to Nigeria are mainly from Europe or Asia. This closure is also based on theoretical reasons based on import substitution policies or theories of infant industries [7]. The, products re-exported from Benin to Nigeria at a relatively lower cost than local products, thus undermining the competitiveness of Nigerian companies. As a result, stricter controls have been introduced at the Nigerian borders to prevent goods from Benin from entering Nigeria. In similar contexts, the literature shows that strict controls at the border or at checkpoints can only limit the entry of unwanted products. This reflects the trade permeability notion. We define the permeability of a trade as indicator which determine the capacity of a country to followed import or export when the border is closed. Specifically, the import permeability between two countries is the share of imports when the borders are closed in the imports an open border case during a period and the export permeability between two countries is the share of exports in a closed border situation in the exports an open border case during a period. It is important to noted that the import values of Nigeria to Benin in 2019 are known and available on the ITC website https:www.intracen.org. This data takes into account the closure of the Nigerian border in 2019 which lasted four months. Our approach is to first estimate these import and export values if the border was not closed using the nonparametric model. After that, we can evaluate the different permeability over the whole year 2019 and over the four months of closure. Recently, the problem of the effects of the Nigeria land borders closure on Benin based has been investigated in a publication such as [3]. The authors have shown that the closure of Nigerian borders has a negative impact on the Benin economy with respect to its total exports based on some fundamental assumptions such as: The simulations were made taking into account the average trade trend between Benin and the rest of the world over the last two years. We believe that this assumption is too strong for the efficient of the projection because the share of imports and exports between Benin and Nigeria at the world level depends according to the previous assumption only on the average between led shares of 2017 and 2018. Moreover, the authors have not studied the concept of permeability of trade. Thus, we will remove this assumption and use data from 1977 to 2018 for the different projections with a nonparametric approach, and we will propose a consistence estimator of the permeability in land closure borders case. In this paper we will propose a multivariate kernel, which satisfied the consistency assumptions of nonparametric regression estimator developed in [9]. In other to substantiate our approach, we will prove that the nonparametric model is more efficient than the multivariate linear regression model under the root mean square error criteria. Using this proposed kernel, we will project the import value of Benin from Nigeria for the year 2019 an open border case. Moreover, the export value from Benin to Nigeria will be estimated for the same year 2019 an open borders case. Based on these trade estimators, we will propose a consistent result for our import and export permeability estimator. At the end, the estimation of the indicators (import and export values, import and export permeability) will be calculated and analyzed. In the following, we will give a literature review in section 2 on trade values. In section 3, we will develope the methodological tools on nonparametric kernel regression model and the modelling result of import and export. As an application, we will evaluate the permeability result of Benin for the year 2019 with a land Borders Closure case in section 4. 2. Literature Review
- Economic liberalism has long traversed the history of economic thought. Several generations of researchers have tried to justify the merits of free trade policies without having a consensus and convincing justifications (e.g. [6]). Others concluded that trade liberalization has not benefited the poorest countries [22]. Some authors justify their ideology by the fact that, except Great Britain, all the major powers have developed through protectionism. The development trajectories of the United States, Japan, Germany and Russia, South Korea and Taiwan are perfect illustrations of Friedrich List’s protectionist theses [22]. The difficulty very often in the application of the rigors of protectionism is that borders are permeable to the point where some products manage to infiltrate the territories, either to fill the gap between local supply and demand, or through a formal or illegal way to compete with local products. In a broader context, several authors have addressed the issue of estimating imports and exports that are, among other things, indicators for measuring border permeability. In the case of US import demand, Riker [20] introduced the regional expenditure level, international trade costs, regional price index for the industry and domestic product price. A similar analysis by Emran [2] incorporates, as explanatory variables for total imports, consumption of domestic goods, and import price index/consumer price index. Through a multilevel approach, Zhang et al. [28] show that the price index, exchange rate, GDP or any of the final expenditure categories (private consumption, government expenditure, investment and export). Some authors (e.g. [17], [18]) introduced GDP per capita, infrastructure investment, real effective exchange rate, and urban population numbers. Moreover Ngoma [14] showed that the geographical distance between the country, the level of inflation for the importing and exporting country (represented by the CPI), trade openness determines the import. With respect to exports, Yazici [27] estimates export demand functions for Turkish agriculture using the boundary test approach to cointegration and error correction modelling. His model was based on world real income, domestic export price, world export price, and exchange rate. In a recent study, Huissain [11] examine the determinants of export supply in Pakistan. Using an Autoregressive Distributed Lag (ARDL) model, these authors measure the effects of relative price (the ratio of export price to domestic prices), production cost (represented by the producer price index), production capacity, and domestic demand pressure on exports.
3. Methodological Tools
- In this section, we will develop the scientific methods for modelling export and import between two countries. We will firstly define the nonparametric regression function model and consistency result of the kernel regression estimator. A new multivariate kernel, which satisfied the consistency assumption of the nonparametric regression estimator, is proposed. At the end, we will present the evaluation method of import permeability and export permeability indicators.
3.1. Nonparametric Kernel Regression Model
- Let X be a random variable in
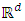 and
and 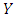 a real random variable. The non-parametric regression model is given by:
a real random variable. The non-parametric regression model is given by: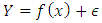 | (1) |
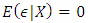 and f is a function of
and f is a function of 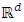 in
in 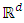 whose form is not predefined. The model (1) was developed by Herman [9]. This author has reviewed a reviewed a non-parametric estimator of the regression function
whose form is not predefined. The model (1) was developed by Herman [9]. This author has reviewed a reviewed a non-parametric estimator of the regression function 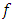 of model (1) and also studied the asymptotic properties of the proposed estimator. It is easy to prove that the function
of model (1) and also studied the asymptotic properties of the proposed estimator. It is easy to prove that the function 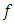 respect
respect 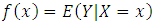 For this purpose, if
For this purpose, if 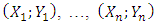 denotes a sequence of random variables i.i.d. of the same law as (X, Y), according to Nadaraya [13] and Waston [25], kernel regression estimators are a local weighted average of the
denotes a sequence of random variables i.i.d. of the same law as (X, Y), according to Nadaraya [13] and Waston [25], kernel regression estimators are a local weighted average of the 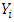 , given by
, given by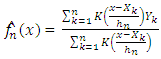 | (2) |
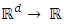 is the kernel function,
is the kernel function, 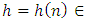
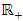 is the bandwidth and
is the bandwidth and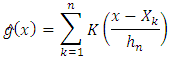 is the Rosenblatt-Parzen (see [21] and [16]) kernel density estimator of the marginal density g of X. Through this paper, we assume that:(A1) K is a Holder continuous, i.e.,
is the Rosenblatt-Parzen (see [21] and [16]) kernel density estimator of the marginal density g of X. Through this paper, we assume that:(A1) K is a Holder continuous, i.e.,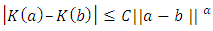 | (3) |
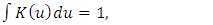 | (4) |
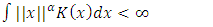 | (5) |
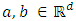 and for some
and for some 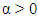 with
with 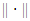 denotes Euclidean norm on
denotes Euclidean norm on 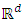 .(A2) The function
.(A2) The function 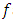 and marginal density
and marginal density 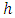 are Holder continuous.(A3) The conditional moments of
are Holder continuous.(A3) The conditional moments of 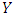 given
given 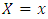 are bounded in the sens that there are positive constants
are bounded in the sens that there are positive constants 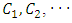 so that for
so that for 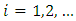
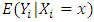
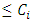 for all x.(A4) The marginal density
for all x.(A4) The marginal density 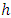 of X is bounded from below on the support of
of X is bounded from below on the support of 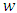 .(A5) The marginal density h of X is compactly supported. Remark 1. Assumption (A3) is substantially weaker than the boundedness conditions on Y that have been imposed by a number of authors, starting with Nadaraya [13]. This condition may be weakened to only a certain finite number of conditional moments being bounded. The assumption (A4) allows handling of the random denominator of
.(A5) The marginal density h of X is compactly supported. Remark 1. Assumption (A3) is substantially weaker than the boundedness conditions on Y that have been imposed by a number of authors, starting with Nadaraya [13]. This condition may be weakened to only a certain finite number of conditional moments being bounded. The assumption (A4) allows handling of the random denominator of 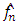 . Also, since by (A2), f and h are assumed to be continuous beyond support of w, such as those described by Rice et al. [19]. The condition (A5) may be weakened to either the existence of many moments of X, or to the compact support of K. The estimator
. Also, since by (A2), f and h are assumed to be continuous beyond support of w, such as those described by Rice et al. [19]. The condition (A5) may be weakened to either the existence of many moments of X, or to the compact support of K. The estimator 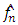 is a function of the bandwidth
is a function of the bandwidth 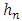 . So how can we optimally choose
. So how can we optimally choose 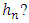 This question was solved by Hardle W. and Marron J. J. [8] as follow: Suppose that
This question was solved by Hardle W. and Marron J. J. [8] as follow: Suppose that 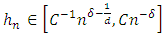 for some constants C,
for some constants C, 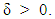 A bandwidth-selected rule
A bandwidth-selected rule 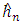 is a
is a 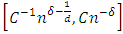 -valued function of,
-valued function of, 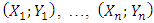 This condition on
This condition on 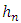 may appear somewhat restrictive because minimization is being performed over an interval whose length tends to zero. This is not a severe restriction because in order to obtain the consistency of
may appear somewhat restrictive because minimization is being performed over an interval whose length tends to zero. This is not a severe restriction because in order to obtain the consistency of 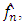 the bandwith must satisfy some similar condition. In our work, a bandwidth-selection rule is given with respect to the Averaged Squared Error (ASE)
the bandwith must satisfy some similar condition. In our work, a bandwidth-selection rule is given with respect to the Averaged Squared Error (ASE)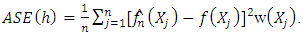 | (6) |
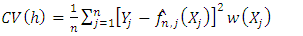 | (7) |
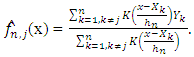 | (8) |
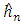 may be also be thought of terms of choosing h to make
may be also be thought of terms of choosing h to make 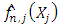 an effective predictor of
an effective predictor of 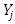 .In the following, we introduce the asymptotic properties of the nonparametric regression estimator defined by relation (2). Theorem 3.1. [8] If (A1), (A2) and (A5) hold, then the estimator
.In the following, we introduce the asymptotic properties of the nonparametric regression estimator defined by relation (2). Theorem 3.1. [8] If (A1), (A2) and (A5) hold, then the estimator 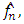 of f is consistent.This theorem is very useful in modelling based on nonparametric kernel regression estimation because it gives a sufficient condition for the convergence of
of f is consistent.This theorem is very useful in modelling based on nonparametric kernel regression estimation because it gives a sufficient condition for the convergence of 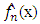 to f(x) when sample seize is large and uniformly in
to f(x) when sample seize is large and uniformly in 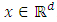 . In our application, we will construct some kernel
. In our application, we will construct some kernel 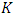 that satisfies the sufficient conditions of the Theorem 3.2. Theorem 3.2. [8] Under the conditions (A1)-(A5), the bandwidth-selection rule, ‘‘choose
that satisfies the sufficient conditions of the Theorem 3.2. Theorem 3.2. [8] Under the conditions (A1)-(A5), the bandwidth-selection rule, ‘‘choose 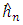 to minimize CV(h)”, is asymptically optimal with respect to the Averaged Squared Error (ASE) defined by (6).
to minimize CV(h)”, is asymptically optimal with respect to the Averaged Squared Error (ASE) defined by (6).3.2. Multivariate Kernel
- In this section we will propose a multivariate kernel function, and we will prove that this kernel function satisfied the assumption (A1). The multivariate kernel which is considered in this paper is defined by
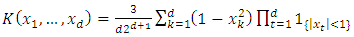 | (9) |
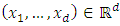 . This kernel is called additive average kernel. Theorem 3.3. The additive average kernel K define by (9) satisfied:(a)
. This kernel is called additive average kernel. Theorem 3.3. The additive average kernel K define by (9) satisfied:(a) 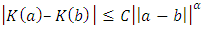 , for all
, for all 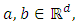 (b)
(b) 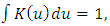 (c)
(c) 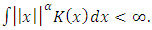 Proof. (a) Let
Proof. (a) Let 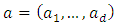 and
and 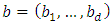 two points of
two points of 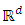 . One has
. One has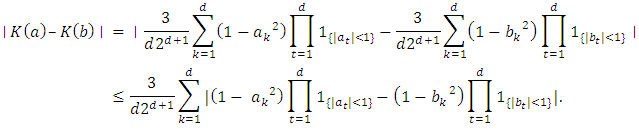 | (10) |
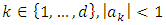 and
and 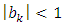 then using relation (10) we deduce that
then using relation (10) we deduce that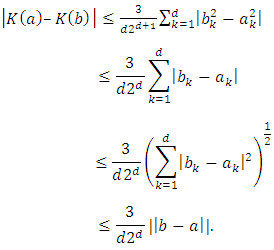 • If for all
• If for all 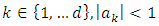 and there exist
and there exist 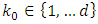 such that
such that 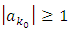 then by using the previous point, we get the result.• If there exists
then by using the previous point, we get the result.• If there exists 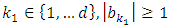 and there exist
and there exist 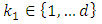 such that
such that 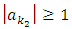 then by using the previous point, we get the result.Then
then by using the previous point, we get the result.Then 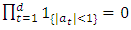 and
and 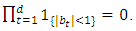 In all cases the point (a) is satisfied with
In all cases the point (a) is satisfied with 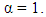 The point (b) is evident. Moreover, the proof of (c) follow provided that the support of K is a compact set.
The point (b) is evident. Moreover, the proof of (c) follow provided that the support of K is a compact set.3.3. Trade Permeability
- In this section, we will give the definition and the evaluation approach of the permeability indicators.Definition 1 (Import Permeability). The Import Permeability between two countries is the share of imports in a closed border situation in the imports an open border case during a period.Let
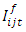 be the import value of a country from a market j when the borders are closed between the country i during a period t and j and Iijt the import value of a country i from a market j an open border case during the period t. The import permeability between the countries i and j is given by
be the import value of a country from a market j when the borders are closed between the country i during a period t and j and Iijt the import value of a country i from a market j an open border case during the period t. The import permeability between the countries i and j is given by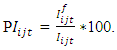 | (11) |
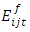 be the export value of a country i from a market j when the borders are closed between the country I during a period t and j and
be the export value of a country i from a market j when the borders are closed between the country I during a period t and j and 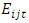 the export value of a country i from a market j an open border case during the period t. The export permeability between the countries i and j is given by
the export value of a country i from a market j an open border case during the period t. The export permeability between the countries i and j is given by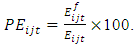 | (12) |
4. Application
4.1. Trade Exchange between Benin and Nigeria
- The border between Benin and Nigeria induces a space whose dynamism varies according to the border segments between the two countries [10]. This dynamism has induced in time a strong dependence of Benin on Nigeria in matters of petroleum and manufactured products, while the opposite is observed in the field of agricultural products (see [10] and [15]).During the period from 1977 to 1990, Benin’s economy recorded formal imports from Nigeria far in excess of exports. This reflects a trade balance deficit between the two countries. In 1994, there was a break in the trend, with formal exports exceeding formal imports. Such a result is justified by the monetary policy of the WAEMU zone, which devalued the CFA franc in 1994. The economic recovery following the devaluation significantly increased exports of raw materials and manufactured goods, and the competitiveness of Beninese companies. This period of economic recovery is characterized by a high inflation rate in Benin. Figure 1 below provides an overview of the movement of formal trade between the two countries during the underlying period.
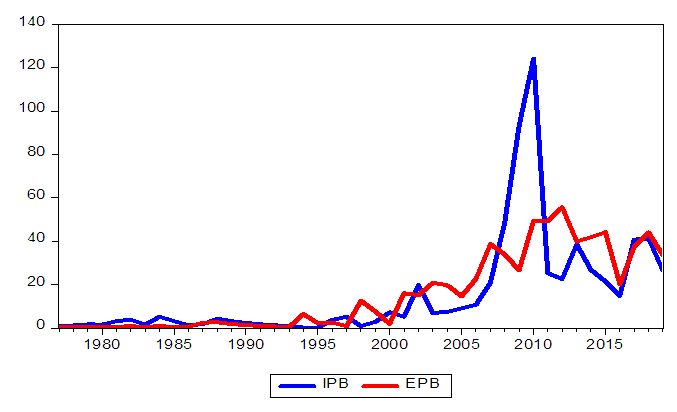 | Figure 1. Evolution of exports and imports between Benin and Nigeria in billion CFA |
4.2. Modelling of Import and Export
- The import and export values between Benin and Nigeria are known in border closed condition over 2019. But in border closure condition those values are not available. In the following, we will use the nonparametric model to estimate the import and export values between Benin and Nigeria in the case of open trade. In view of the results of the literature, we have studied the following variables as: Consumer Price Index of Benin (CPIB), Gross Domestic Product of Benin (GDPB), Gross Domestic Product of Nigeria (GDPN), Benin’s Population size (POPB), Nigeria’s population size (POPN), Benin’s Primary School Enrolment Rate (PSERB), Benin’s Imports from Nigeria (IPB) and Benin’s Exports to Nigeria (EPB).Table 1 shows the p-value of the significance test of the correlations between the different variables. This test rejects the null hypothesis (H0: coefficient of correlation =0) if the p-value is less than 0.05. This Pearson correlation test between the variables shows that there is a significant correlation between the variables. Using the Table 1, we model Benin’s imports from Nigeria by:
|
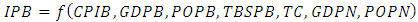 | (13) |
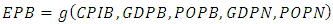 | (14) |
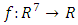 and
and 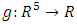 are unknown real functions. In the following we will estimate the functions f and g by the nonparametric approach developed in section 3.1.It is well known that the nonparametric model is a model which is independent of linear assumption on the link function. In the following, we have evaluated the performance of this nonparametric model to multivariate linear regression model by using the criteria of Root Mean Square Error (RMSE):
are unknown real functions. In the following we will estimate the functions f and g by the nonparametric approach developed in section 3.1.It is well known that the nonparametric model is a model which is independent of linear assumption on the link function. In the following, we have evaluated the performance of this nonparametric model to multivariate linear regression model by using the criteria of Root Mean Square Error (RMSE): 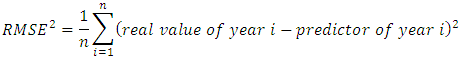 The errors of nonparametric kernel regression (Model 1) and multivariate linear regression model (Model 2) are presented in Table 2.
The errors of nonparametric kernel regression (Model 1) and multivariate linear regression model (Model 2) are presented in Table 2.
|
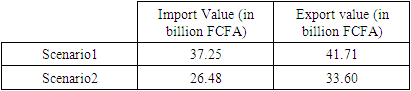
4.3. Permeability Result
- In order evaluate the effect of the closure between Benin and Nigeria we have consider two scenarios: Scenario 1 (Borders between Benin and Nigeria were not closed thru 2019) and scenario 2 (Borders between Benin and Nigeria were closed in 2019). The trade results in scenario 2 are not estimated because the real values exist. Then we use the nonparametric model to estimate the export and import values from Benin to Nigeria. Based on the nonparametric regression model, we denote by
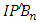 and
and 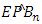 estimation of import and export (see model 2) with n the sample size and multivariate kernel K defined by 9. We assume that (A6) the variables IPB, EPB, CPIB, GDPB, POPB, PSER, ER, GDPN POPN are bounded in the year. Then We estimate the import and export permeability respectively by:
estimation of import and export (see model 2) with n the sample size and multivariate kernel K defined by 9. We assume that (A6) the variables IPB, EPB, CPIB, GDPB, POPB, PSER, ER, GDPN POPN are bounded in the year. Then We estimate the import and export permeability respectively by: 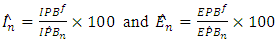 | (15) |
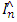 and
and 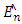 are consistents.Proof. Using the Theorem 3.3 the kernel K satisfied the assumption (A1) and (A2). Moreover, by Theorem 3.3, the estimator
are consistents.Proof. Using the Theorem 3.3 the kernel K satisfied the assumption (A1) and (A2). Moreover, by Theorem 3.3, the estimator 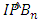 of import converge almost surely (a.s.) to the real value IPB which is different to zero. Using (A6) the condition (A3)-(A5) are satisfied. Then
of import converge almost surely (a.s.) to the real value IPB which is different to zero. Using (A6) the condition (A3)-(A5) are satisfied. Then 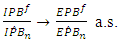 Similarly, on has
Similarly, on has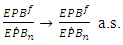 The proof of the theorem is completed.The previous Proposition 4.1 given us a consistence estimator of import and export permeability for a year. The result of our estimation for 2019 are presented in the Table 3.
The proof of the theorem is completed.The previous Proposition 4.1 given us a consistence estimator of import and export permeability for a year. The result of our estimation for 2019 are presented in the Table 3.
|
|
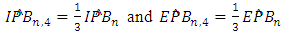 | (16) |
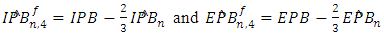 | (17) |
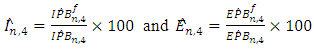 | (18) |
|
5. Conclusions
- Border permeability plays an important role in the selection of economic and financial intelligence strategies. This study developed a non-parametric estimation model to estimate trade (imports and exports) between Benin and Nigeria in 2019, in order to assess the economic or trade permeability of the two borders. The results show that the non-parametric estimation method has a better property in predicting exports and imports than the parametric models. The strong growth of the trade balance (62.94%) between Benin and Nigeria noted during the year 2019 compared to trade balance in normal situation shows that Benin has achieved a low rate of import with the closure of borders. The results also show that despite the policies of strengthening customs barriers put in place by Nigeria, around the formal land borders between Benin and Nigeria, some goods manage to infiltrate both sides of the borders. 41.66% permeability of goods for export and 13.26% permeability for import were recorded in the last four months when land borders between Benin and Nigeria was closed in 2019, after the closure of the land borders. This is a testimony that the ability of the products to infiltrate the formal channels of the two countries, in the situation of closure of borders. We project to study the economic impact of the border closure between the two countries based on nonparametric considering the effect of COVID19, which continues to create a lot of economic damage in the world. Moreover, we intend to use this nonparametric approach in the work of optimal learning and deterministics self-awareness statements [24].
ACKNOWLEDGEMENTS
- We thank all those who have contributed to the improvement of the quality of this paper. Special thanks to all reviewers.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML