-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Economics
p-ISSN: 2166-4951 e-ISSN: 2166-496X
2014; 4(2): 114-123
doi:10.5923/j.economics.20140402.03
Monetary Policy in Nigeria: Any Role for McCallum Rule?
Mika’ilu Abubakar1, Baba N. Yaaba2
1Department of Economics, Usmanu Danfodiyo University, Sokoto, P.M.B. 2346, Nigeria
2Department of Statistics, Central Bank of Nigeria, P. M.B. 0187, Abuja, Nigeria
Correspondence to: Baba N. Yaaba, Department of Statistics, Central Bank of Nigeria, P. M.B. 0187, Abuja, Nigeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
The unending debate among policy makers, researchers and market analysts on the suitability of monetary policy rule over discretion prompted the development of models to determine and predict the possible future path of monetary policy. Proponents of rule favour commitment to a specific rule while opponents, although agree with the proponents to some extent but to a large extent prefer discretion, with the notion that central banks cannot outsource critical issues of monetary policy decision making to a simple mechanics of rule. This study determined the applicability of McCallum rule, within the context of bounds test, to Nigeria’s monetary policy framework, using data from 1989Q1 to 2013Q2. With a positive monetary response factor and potential output as well as negative velocity, monetary base can be varied to enhance output growth at low inflation rate, thus guarantees output stability perhaps in the long-run, hence supports the application of the rule by the Central Bank of Nigeria (CBN). The study, however, suggested the introduction of additional monetary variable to the rule to make it more robust as well as constant monitoring of velocity of monetary base considering the observed volatility of the variable during the studied period.
Keywords: McCallum rule, Taylor rule, Monetary policy, GDP
Cite this paper: Mika’ilu Abubakar, Baba N. Yaaba, Monetary Policy in Nigeria: Any Role for McCallum Rule?, American Journal of Economics, Vol. 4 No. 2, 2014, pp. 114-123. doi: 10.5923/j.economics.20140402.03.
Article Outline
1. Introduction
- The unending debate amongst policy makers, academics and market players as to whether monetary policy framework should be based on rule rather than discretion of policy makers have prompted the search and subsequent development of models to determine and predicts the possible future path of monetary policy, using developments in the domestic as well as external sectors of the economy. Advocates of rule believe that, without commitment to a specific rule, there is the possibility of heavy reliance on a particular policy that strives to achieve a particular objective at the expense of others and that the credibility of monetary policy will be in doubt. They also believe that policy rule increases accountability and holds policy makers responsible for underperformance. Although, policy makers seems to agree with the numerous advantages of rules as opined by its advocates and most importantly its ability to facilitate communication with the public, on the policy intentions of the monetary authority, hence enables fair judgement of their performance vis-à-vis the policy objectives. This notwithstanding, however, they, to a large extent, tend to favour discretion, with the notion that central banks cannot outsource such critical and complex issues of monetary policy to a simple mechanics of rule. Their scepticism with regard to rule is also in connection to the ambiguity enshrined in the linkage between policy instruments and the ultimate policy goals. Therefore, policy makers will prefer, in a worst case scenario, a blend of both rule and discretion believing that the two are complimentary. The complementarity of rule and discretion, however, poses the challenge of policy mix. Without any identifiable quantitative challenges with discretion, there is need to determine not only how to decide on the rule but also how to measure performance over time. Popular contributions in this regard are McCallum (1987) and Taylor (1993). Taylor rule gained more prominence because of its simplicity as well as its performance in the United States in the 1990s.McCallum (1987) rule targets nominal gross domestic product (GDP) through money supply. The rule states the need to adjust monetary policy in terms of deviations of GDP from target. For instance, if GDP falls below the desired target, the central bank is expected to increase money supply to stimulate the economy so as to facilitate increase in GDP to the desired level. While Taylor (1993) is of the view that central bankers increase the nominal interest rate, if output is above the potential (output gap) and/or inflation is above the target (inflation gap). In a nutshell, therefore, McCallum rule is a nominal GDP target rule using monetary base as the major policy instrument, while Taylor rule disregards monetary target in preference for interest rate.However, since monetary targeting is still in vogue in Nigeria, it would not be out of place to think that McCallum rule is suitable for Nigeria. This study is, therefore, an attempt to examine the relevance of McCallum rule to the Central Bank of Nigeria (CBN) monetary policy framework.To achieve this, the paper is structured into five sections. Following this introduction is section two which appraises the principles behind McCallum rule, as well as relevant empirical literature. Section three, explains the data sources and methodology, while section four presents the empirical results and the last section concludes the study.
2. Review of McCallum Rule
2.1. Theoretical Review
- McCallum (1987, 1993) is of the view that central banks should follow a rule in designing monetary policy. McCallum suggest that central banks should target nominal GDP growth rate through the use of monetary base as an operating instrument. He proposed a rule that can be represented mathematically as:
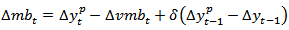 | (1) |
2.2. Empirical Review
- Dean and Stark (1995) use macroeconomic models of Keynes, PSTAR and rational expectations to appraise McCallum rule for the US between 1963 and 1993. They submitted that, McCallum rule on the average seems more appealing than any other monetary policy rule, as the average level of real output was closer to the potential level, while prices were lower in the simulation than the historical data suggested. They, however, suggest the use of growth rate of nominal GDP instead of levels but agreed that the rule overall enhances downward trend in inflationary spiral. Stark and Dean (1998) further expanded the set of economic models based on which McCallum rule was originally tested. They employed Keynesian version, reduced-form model and structural VAR framework as well as impulse response to test the stability of the model using quarterly US data from 1959Q1 to 1993Q2. Their results identified some problems of instability with the original McCallum specification which focused on nominal GDP. The rule according to them performed better, in term of dynamic stability and short term variability measures when growth rate of real GDP is used as against level. They submitted that if the rule is modified to use growth rate of real GDP instead of level, it will serve as a useful tool of monetary policy formulation.Arturo and Mishkin (1996) examine the role of monetary aggregates in the conduct of monetary policy in the United States and Germany for the period 1959 to 1995 using a multivariate VAR concept. They assess monetary aggregates from the perspectives of information variable, indicator of policy action and instrument of policy rule. Their final results confirmed neither the informative nor indicative role of monetary aggregates. It also didn’t provide any strong evidence in support of the potency of monetary aggregates as instrument of policy rule for both countries. Esanov et al. (2004) use an eclectic approach to review the rule-based behavior of the Central Bank of Russia with regard to the conduct of monetary policy from 1993 to 2002. They assess the reaction of the bank to exchange rate, inflation and output gap. Their results show that between 1993 and 2002, the bank used monetary aggregates as an instrument of monetary policy which conforms to the McCallum proposition.Vdovichenko and Victoria (2004) investigate the policy rule type adopted by the Bank of Russia between 1993 and 2003. With special focus on econometric modelling of monetary policy rules of various types, they employed different econometric techniques, such as generalized method of moments (GMM), ordinary least squares (OLS) and two-stage least squares (TSLS) with modifications in term of adopting two set of simultaneous equations that describes the dynamics of intervention in the foreign exchange market and sterilisation of excess liquidity. The results show a stabilizing pattern in the management of base money and that the format of interest rate policy was more of adaptive in nature. The results also reveal that the Bank was more interested in exchange rate regulation as against the inflation officially pronounced by the Bank.Kong (2007) reviews the conduct and characteristics of Chinese monetary policy from the first quarter of 1994 to the fourth quarter of 2006 by estimating the monetary policy reaction function via a quantity theory of money like model. He finds that although all the estimated rules describe Chinese monetary policy stance to some extent but Taylor rules performs better than McCallum rules in evaluating Chinese monetary policy stance during the period.Shuzhang et al. (2008) uses a counterfactual simulation method to assess the possibility of McCallum rule policy framework for China based on two distinct macroeconomic models from 1994Q1 to 2009Q1. The results show that McCallum rule is capable of stabilizing growth rate of China and that monetary base rule can be used as a benchmark for monetary policy decisions in China.Tuuli et al. (2008) examine the applicability of McCallum monetary policy rule based on money supply with inflation objective for mainland China for the period 1996 to 2008. They examined the informative content of the concept of excess money compared to rule-based values for forecasting inflation. The results confirmed the usefulness of monetary aggregates in forecasting both consumer and corporate goods prices. They, however, argued that results for consumer prices depend on the time horizon of the forecast. They concluded that the movement in the Chinese monetary base tracked fairly well the McCallum rule and that it can be used to detect shocks to Chinese monetary policy.Diez de los Rios (2008) also supported the proposal of McCallum (1987) which suggest the need for a monetary rule that will guide policymakers to the possibility of fluctuations in exchange rates. He estimates monetary policy reaction function using an affine term structure framework for Canada, Germany and the U.K for the period January 1979 to December 2005. The results suggest that, unlike the earlier results, the monetary authorities of the studied countries react to movements in nominal exchange rate.Ghatak and Moore (2008) examine the monetary policy reaction function based on both Taylor and McCallum rules for the transition economies of the Czech Republic, Hungary, Poland, Slovakia, Slovenia, Bulgaria and Romania between 1994 and 2006 using vector autoregression. The results show that while monetary aggregate in Bulgaria, Czech Republic, Hungary, Poland, Romania, Slovakia and Slovenia, react to inflation variants in the long-run, the deviation of exchange rates from the potential level can be attributed to the vagaries of short-term interest rates. They submitted that the Taylor rule is far more applicable to exchange rate targeting, whereas McCallum rule is suitable for inflation targeting. Shuzhang (2010) evaluates the relevance of McCallum rule to the Chinese monetary policy guideline. He applied a structural VAR to China’s quarterly data from the first quarter of 1994 to the first quarter of 2009. The results strongly support the use of the rule as a medium to long-term policy framework for monetary policy formulation as it is capable of stabilizing the economy, reduce policy uncertainties, increase credibility as well as improve transparency of monetary policy.Michael and Kapur (2012) examine the operational performance of McCallum rule, Taylor rule and their respective hybrid versions for India using quarterly data from 1996 to 2011. The results reveal that, the forward-looking nominal output objective formulations of both rules and their hybrid versions, using interest rate as an operating instrument, performed better than the backward-looking specifications. They, therefore, argued in favour of the adoption of the forward-looking formulations of the rules for India.Giray (2012) estimates a reaction function of the Central Bank of the Republic of Turkey (CBRT) based on Taylor rule, as well as what he referred to as ‘Hybrid McCallum-Taylor rule’. The data covered the period 2003Q1 to 2012:Q1. He used Generalized Methods of Moments (GMM) and Limited Information Maximum Likelihood (LIML) methods to estimate the reaction function covering the period of inflation targeting in Turkey, with nominal interest rate as the instrument of monetary policy. The results reveal that Taylor rule specifications are more applicable to the monetary policy guideline of the Central Bank of Republic of Turkey (CBRT).
3. Methodology and Data Sources
- Equation (1) implies that, if output gap is negative, the base money should be adjusted downward to reduce the rate of overheating in the system. Similarly, negative inflation gap should also attract reduction in the money supply.From equation (1), therefore:
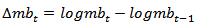 | (2) |
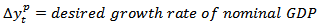 | (3) |
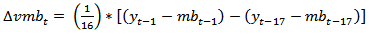 | (4) |
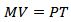 | (5) |
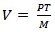 | (6) |
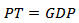 | (7) |
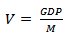 | (8) |
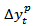 is the sum of inflation target and long-run average real GDP growth rate. Following, Baoli (2010), equation (1) can be modified to avoid the possibility of interpreting McCallum rule as mainly a price stability reaction.
is the sum of inflation target and long-run average real GDP growth rate. Following, Baoli (2010), equation (1) can be modified to avoid the possibility of interpreting McCallum rule as mainly a price stability reaction.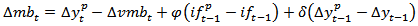 | (9) |
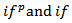 are inflation target and inflation respectively. Although, Central Bank of Nigeria (CBN) is not an inflation targeter but it has long been striving to achieve single digit inflation, hence
are inflation target and inflation respectively. Although, Central Bank of Nigeria (CBN) is not an inflation targeter but it has long been striving to achieve single digit inflation, hence 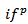 will be proxied by the upper bound of single digit (i.e. 9.99), while Hodrick-Prescott (HP) filter (1997) will be applied to GDP growth rate to derive the potential GDP as well as the corresponding GDP gap.If
will be proxied by the upper bound of single digit (i.e. 9.99), while Hodrick-Prescott (HP) filter (1997) will be applied to GDP growth rate to derive the potential GDP as well as the corresponding GDP gap.If 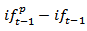 is represented as fg and
is represented as fg and 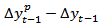 is denoted as yg, then equation (9) can be reformulated as:
is denoted as yg, then equation (9) can be reformulated as: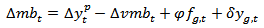 | (10) |
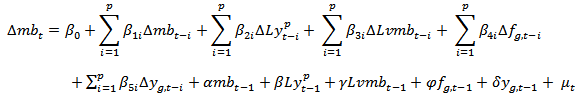 | (11) |
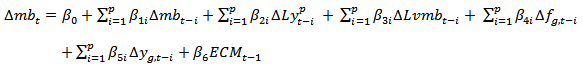 | (12) |
4. Analysis of Results
4.1. Statistical Properties of the Data
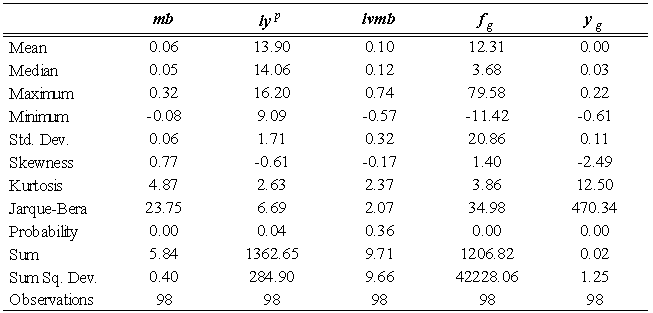
- To determine the statistical properties of the data used for the estimation, summary statistics and correlation coefficients of the variables were calculated. Unit root tests were also conducted on the data to determine their level of stationarity and the results are reported in Table 1 to 3. The summary statistics of the variables used for the estimation are reported in Table 1. The table indicates that there are ninety eight observations in all. While the growth rate of monetary base (mb) recorded a mean observation of 0.06, the potential growth (lyp) stood at 13.90. The mean observation of the output gap (yg) is almost zero. While fg has the minimum value of -11.42, the minimum value of lyp is 9.09. The log of velocity recorded a minimum of -0.57 and maximum of 0.74 showing that the variable was volatile during the sample period.
|
|
|
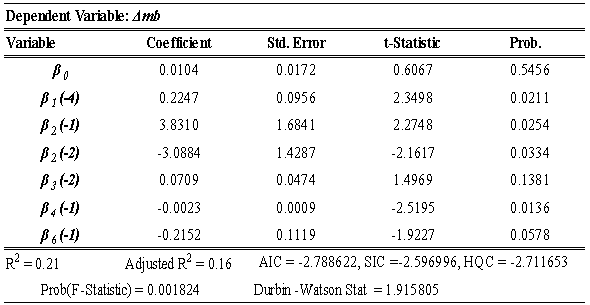
4.2. Analysis of the Empirical Results
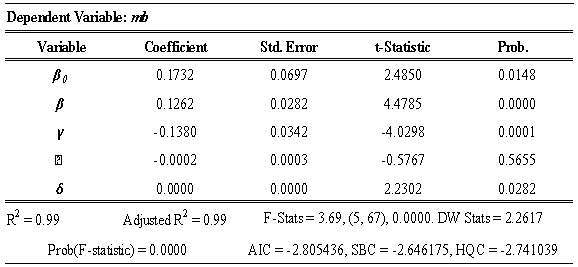
- To affirm the validity of McCallum rule as modeled in equation (11), change in monetary base will be a direct function of change in output gap. This is referred to as the monetary response factor and it is one of the most critical terms in McCallum rule as it is essential for the stabilization of output and to some extent price level (Shuzhang et al, 2008). This is so, because, the gap of nominal income growth term (δ) is defined as the trend growth of gross domestic product (GDP) minus actual growth of GDP such that as growth in actual output fall short of its potential, monetary policy becomes expansionary so as to close the gap. The accommodative monetary policy stance of the monetary authority is adjudged by the positive response of the growth rate of base money. Hence, output gap is apriori expected to return positive sign. Positive output gap, in this case, portrays that the economy still has spare capacity to produce more, hence, serves as a signal to the central bank that more money is needed in circulation to enhance the productive capacity of the economy. The long-run result presented in Table 4, in consonance with the principles of McCallum rule, indicates that both potential output and the corresponding output gap are directly a function of monetary base. In other words, both the monetary response factor as well as the potential output yielded positive signs in agreement with the workings of the McCallum rule.
|
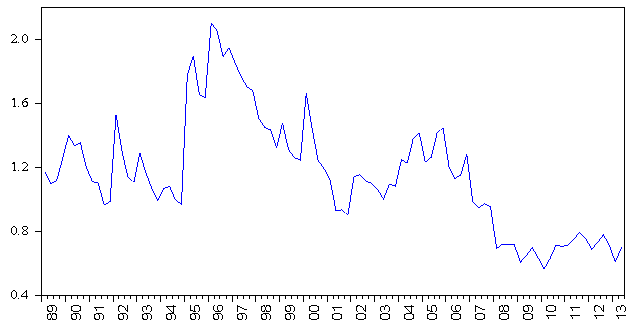 | Figure 1. Velocity of Monetary Base, 1989Q1 to 2013Q2 |
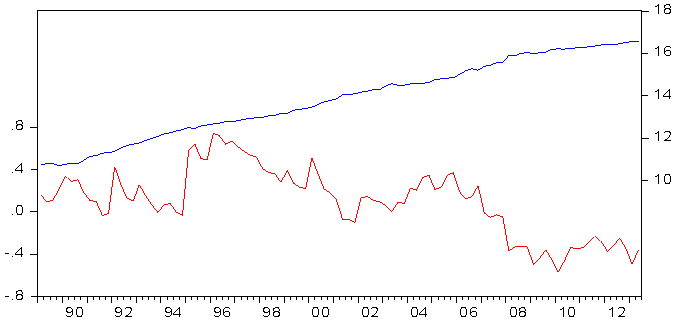 | Figure 2. Monetary Base Vs its Velocity in Nigeria, 1989Q1 to 2013Q2 |
|
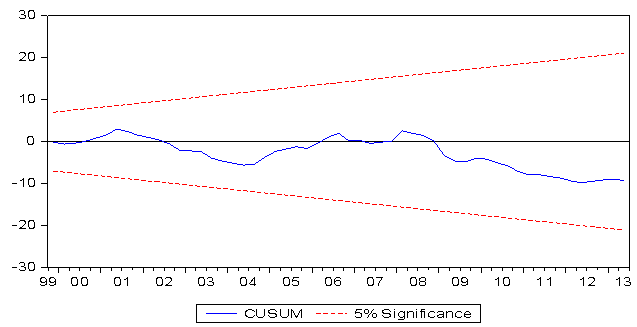 | Figure 3. Cumulative Sum of Residual Test |
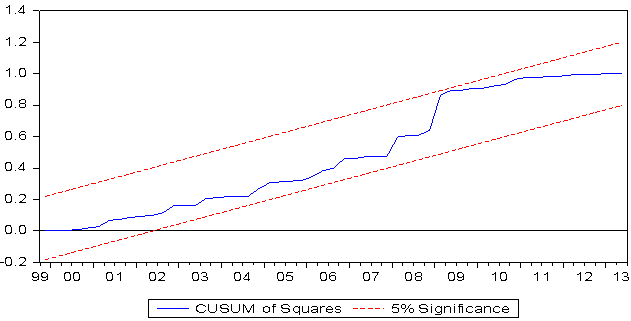 | Figure 4. Cumulative Sum of Squares Recursive of Recursive Residual Test |
5. Conclusions and Policy Options
- The unending debate on the possibility of rule based monetary policy framework have ignited search for rule, the result of which is the emergence of McCallum rule amongst others. This paper attempts to test the applicability of McCallum rule to the Nigeria’s monetary policy framework within the context of bounds tests approach to cointegration developed by Pesaran et al (2001), using data from the first quarter of 1989 to the second quarter of 2013. The study utilized cumulative sum of recursive residual and cumulative sum of squares recursive residual to test the stability of the estimated parameters.While the coefficients of output gap and the velocity of monetary base, which are the first two most critical terms in the rule are properly signed, that of inflation gap is not. The potential output and the corresponding output gaps are positively signed, while the velocity of circulation of the monetary base is negatively signed and statistically significant in line with the workings of the rule.Over all, the results show that McCallum rule can serve as a potent monetary policy rule for the Nigeria’s monetary policy framework. Considering the positive monetary response factor (δ) as reported in Table 4, as well as the negative velocity and positively signed potential output, McCallum rule provides promising signal for the possibility of variations in mb to enhance output growth at desirable level of prices, hence guarantees output stability perhaps in the long-run. However, since the idea of monetary policy rule (both non-activist rule-such as that of Friedman Milton and activist versions- such as McCallum and/or Taylor rules) seems not appealing to monetary authorities, the study suggests that the CBN should adopt the rule as a consultative yardstick or illustrative benchmark to guide the monetary policy committee (MPC) in taking discretionary monetary policy decisions. In other words, the McCallum framework should be officially commissioned and results made available to MPC members at least one week before MPC meetings. This will serve as additional information to committee members.Furthermore, additional factors can be introduced to the rule. The current structure of the rule relies extremely on mb which is just one of the numerous instruments of monetary policy. Therefore, some other monetary policy variables can be introduced to the rule to make it more robust.It is, however, important to note the need for caution when using the rule as a benchmark or a guide, considering high volatility of velocity. The velocity of monetary base ranges between 0.6 and 2.1 during the studied period which mirrors the non-predictable nature of the behavior of economic agents. Macroeconomics has, however, not provided adequate theory capable of predicting human behavior, hence, velocity should be properly monitored so as to continuously update policy makers on the dynamic responses of humans to variations in policies.
Notes
- 1. McCallum revised the earlier version of the rule using nominal GDP growth as the target.2. McCallum used annual data which yields four years, but according to Michael and Kapur (2012) average growth rate of velocity for quarterly data is sixteen quarters = (1/16)*[(xt-1 – bt-1)-(xt-17-bt-17)]3. Inflation or output.4. PSTAR was developed by Herb Taylor of the Federal Reserve Bank of Philadelphia in the late 80s to support monetary policy formulations.5. Growth rate of nominal output exceeds target or the desired level.6. Inflation rate exceeds target or the desired level.7. Represented as yg in equations (10) and (11).8.
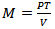 9. The Cambridge school later modified the equation as: M = kPT10. They are not as strong as suggested by McCallum as he alluded a base money response of between 0.25 to 0.50 for industrialized and emerging economies (Michael and Muneesh, 2012).11. As well as potential output.
9. The Cambridge school later modified the equation as: M = kPT10. They are not as strong as suggested by McCallum as he alluded a base money response of between 0.25 to 0.50 for industrialized and emerging economies (Michael and Muneesh, 2012).11. As well as potential output. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML