-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Economics
p-ISSN: 2166-4951 e-ISSN: 2166-496X
2013; 3(3): 140-148
doi:10.5923/j.economics.20130303.02
The Fluctuation of the Prices of Crude Oil at International level explained by a Dynamic Discrete Stochastic Models
Yohannes Yebabe
School of Mathematical and Statistical Sciences, Hawassa University, P. O. Box 05, Hawassa, Ethiopia
Correspondence to: Yohannes Yebabe, School of Mathematical and Statistical Sciences, Hawassa University, P. O. Box 05, Hawassa, Ethiopia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Most energy consuming activities in the world are dependent on energy sources from crude oil. One of the characteristics of the price of crude oil is its high scale of wavering that can directly or indirectly affect the economic progress for both oil exporter and importer nations. The main aim of this study is to assess the fluctuations of the monthly average price of crude oil and price shocks at the international market using the daily recorded data from 1st Jan 2003 to 31st Dec 2012 from OPEC. The Autoregressive Moving Average model with exogenous inputs model (ARMAX) is used as an empirical model. The result of the study reveals that the ARMAX(2,0) discrete stochastic model captures the fluctuation of the log-transformed monthly average price with exogenous inputs of annual-time specific effects. In normal conditions we expect that the price shock is higher at higher price of the commodity. However, astonishingly the monthly average price of crude oil and the price shock in the international market are found to be uncorrelated. The ARIMAX(2,2,1) discrete stochastic model captures the fluctuation of the log-transformed price shock on crude oil with no exogenous input. In general, the problem of handling the fluctuation of the price of crude oil in the international market is not only attributed to unorthodoxies from the mean but also problems of price shocks emanating from unknown factors.
Keywords: Galton Distribution, Crude Oil Price, Price Shock on Crude Oil and ARMAX Models
Cite this paper: Yohannes Yebabe, The Fluctuation of the Prices of Crude Oil at International level explained by a Dynamic Discrete Stochastic Models, American Journal of Economics, Vol. 3 No. 3, 2013, pp. 140-148. doi: 10.5923/j.economics.20130303.02.
Article Outline
1. Introduction
1.1. Background
- Technologically advanced societies have become increasingly dependent on peripheral energy sources for transportation, the production of many manufactured goods, and the conveyance of energy services. Globally, energy consumption grew more rapidly than the global economy, meaning that the energy intensity of economic activity increased. The energy markets have pooled crisis recovery and strong industry dynamism. This implying that, each nation in the world faces the challenge to achieve rapid economic development and sustainable supply of energy. Many economists mentioned that there is strong interdependence between the volume of energy consumption and economic development of a given nation. Whenever the energy consumption of the given nation is high, it is observed that the GDP of that nation somehow showed a positive change[1,2]. Among the principal energy sources of the world, oil is the largest (above 33%) and its prices have increased dramatically. Succeeding to oil, coal posted a budding role in the world's energy consumption. For instance, in 2008 coal accounted nearly for 27% of the other energy sources of the world. The other energy sources of the world in descending order are gas, nuclear power, hydroelectric power and others like geothermal power, solar energy, and bio-fuel[3].
1.2. The Vulnerability of Higher Oil Prices on the Oil Importer Nations
- Oil prices tranquil matter to the health of the world economy. However the structures of the price of oil in these recent times have exhibited exceptional volatility. Higher oil prices are recorded since 1999-partly the results of OPEC supply-management policies contributed to the global economic recession in 2000-2001 and are dampening the current cyclical upturn[4]. These higher prices are contributing to stubbornly high levels of unemployment and exacerbating budget-deficit problems in many OECD and other oil-importing nations[5]. The vulnerability of oil-importing nations to higher oil prices varies evidently contingent on the degree to which they are net importers and the oil intensity of their economies. Higher oil prices cause inflation on food prices would nurture by some percentage point. Euro-zone nations would suffer most in the short term, their GDP dropping by 0.5% and inflation rising by 0.5% in 2004. In the same year the United States would suffer the least, with GDP falling by 0.3% and Japan’s GDP would fall 0.4 %[4,6]The antagonistic economic impact of higher oil prices on oil-importing developing nations is generally even more severe than for OECD nations. This is because their economies are more dependent on imported oil and more energy-intensive, and because energy is used less efficiently [7]. India spent $15 billion, equivalent to 3% of its GDP, on oil imports in 2003, which is 16% higher than its 2001 oil-import bill. In 2004 the loss of GDP averages 0.8% in Asia and 1.6% in very poor highly indebted nations in the year following a $10 oil-price increase. In the same year the loss of GDP in the Sub-Saharan African nations would be more than 3%[8]
1.3. Some Known Factors Affecting the Price of Crude oil
- Conferring to Energy Information Administration (2007), crude oil prices have increased has showed dramatic fluctuations latest years. Many economists (Like Abdoulkarim Esmaeili and Zainab Shokoohi[9], Deren Unalmis et al[10], E.S. Dokuchaev et. Al[11], Lutz Kilian [12], etc) claim that the important factors which can affect the global price of the crude oil are: Global changes in Supply by OPEC and Demand by oil importer nations like US, China and European Countries. The since crude oil prices are dependent on the sentiments of the global equity market, the market structure also the factor on the prices of crude oil. Dow Jones Industrial Average Index, NASDAQ and NYSE are few which govern the US equity market and hence the oil prices as well. The movement in Dollar index also changes the oil prices on daily basis. When dollar will go up, oil prices will go down and vice versa. The US labour department also comes out with unemployment report which conveys the unemployment rate in US (negatively correlated with crude oil price). Moreover, Wars, Geopolitical crisis, Recession and Natural Disaster are some other important factors that also momentously affect oil prices.
2. Review Literatures
2.1 Empirical Studies about the Crude Oil Prices
- Yu Wei et al[13] described that the price of crude oil plays important role on the world economy. Therefore, recent increases in oil prices volatility have caused great concern among consumers, corporations and governments. As the extension on the work of Kang et al.[14], this paper tried to capture the volatility of the prices of crude oil using a number of linear and nonlinear GARCH-class models. The result of this study suggested that the nonlinear GARCH-class models have better forecasting accuracy to the long-memory of crude oil prices volatility than the linear ones, especially in volatility forecasting over longer time horizons, such as five or twenty days. Hassan Mohammad and Lixian Su[15] mentioned that crude oil price movements appear to have undesired consequences for the economies of both oil-importing and oil-exporting countries which is associated with high inflation, real exchange rate appreciation, loss of competitiveness, and decline in manufacturing output and employment. According to this paper providing an appropriate model to forecast the future oil prices is important to stabilizes many economic activities of oil both oil-importing and oil-exporting countries. This paper applied several ARIMA-GARCH models for modelling and forecasting the conditional mean and volatility of weekly crude oil spot prices. The result of this study suggested that the crude oil price conditional mean and variance are best forecasted by MA(1)-EGARCH(1,1) and MA(1)-APARCH (1,1) models. H. Mostafaei and L. Sakhabaksh [16] give details that long term memory forecasting of crude oil prices using Box-Jenkins models (ARMA or ARIMA models) may be untrustworthy even for optimal predictions. After showing the weakness of the Box-Jenkins model, the paper preferred to utilize the ARFIMA as an empirical model for the long-term memory prediction of crude oil prices. The finding of this paper suggested that the best fitted model to predict the long-term memory of crude oil prices of OPEC is the ARFIMA
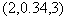 model.Aijun Hou and Sandy Suardi[17] explained that the ability to accurately forecast the price of crude oil is as important concern in both policy and financial arenas. According to the paper main reason why we need to obtain the good model to forecast the prices of crude is that its fluctuations are of significant interest to both financial practitioners and market participants, not least because they affect decisions made by producers and consumers in strategic planning and project appraisals, but also they influence investors' decision in oil-related investments, portfolio allocation and risk management. This paper utilized a nonparametric GARCH model to capture the crude oil price volatility. The result of this study reviles that the nonparametric GARCH model better to predict the price of crude oil than the commonly used parametric GARCH models.Haiyan Xu et al[18] mentioned that the crude oil prices had tended to fluctuate at higher scale dynamism and intensified amplitude since 2004. This paper tried to establish a trend deduction model of the fluctuation of crude oil prices. This model integrates the probability distribution of oil price series with probability distribution of a Markov Chain reveals the short term changing trends of oil prices, while the limit probability of oil price series as a Markov Chain reflects the middle-long term changing trends of oil prices. The difference between them indicates the specific changes in a variety of oil price states from the short-term to the middle-and long terms. This paper also suggested that the probability distribution of the prices of crude oil from 2004-2010 is found to be Galton probability distribution of mean 4.057 and variance 0.2594. Oil markets have been drawing increased interest and participation from investors and financial entities without direct commercial involvement in physical oil markets. The role of these non-commercial futures market participants in recent price developments is challenging to assess, particularly over short time intervals[19]. Therefore, we need to have rigorous quantitative information about the primary explanation for the recent trend in oil prices. Therefore, main motivation of the study is to apply the dynamic discrete stochastic having exogenous input models to capture the fluctuations of monthly average price with its price shock of crude oil at the international market.
model.Aijun Hou and Sandy Suardi[17] explained that the ability to accurately forecast the price of crude oil is as important concern in both policy and financial arenas. According to the paper main reason why we need to obtain the good model to forecast the prices of crude is that its fluctuations are of significant interest to both financial practitioners and market participants, not least because they affect decisions made by producers and consumers in strategic planning and project appraisals, but also they influence investors' decision in oil-related investments, portfolio allocation and risk management. This paper utilized a nonparametric GARCH model to capture the crude oil price volatility. The result of this study reviles that the nonparametric GARCH model better to predict the price of crude oil than the commonly used parametric GARCH models.Haiyan Xu et al[18] mentioned that the crude oil prices had tended to fluctuate at higher scale dynamism and intensified amplitude since 2004. This paper tried to establish a trend deduction model of the fluctuation of crude oil prices. This model integrates the probability distribution of oil price series with probability distribution of a Markov Chain reveals the short term changing trends of oil prices, while the limit probability of oil price series as a Markov Chain reflects the middle-long term changing trends of oil prices. The difference between them indicates the specific changes in a variety of oil price states from the short-term to the middle-and long terms. This paper also suggested that the probability distribution of the prices of crude oil from 2004-2010 is found to be Galton probability distribution of mean 4.057 and variance 0.2594. Oil markets have been drawing increased interest and participation from investors and financial entities without direct commercial involvement in physical oil markets. The role of these non-commercial futures market participants in recent price developments is challenging to assess, particularly over short time intervals[19]. Therefore, we need to have rigorous quantitative information about the primary explanation for the recent trend in oil prices. Therefore, main motivation of the study is to apply the dynamic discrete stochastic having exogenous input models to capture the fluctuations of monthly average price with its price shock of crude oil at the international market. 3. Objectives
- We wish to fit an econometric model capture the fluctuation of the monthly average price of crude oil and the price shock within the month as an Autoregressive Moving Average with exogenous input (ARMAX) model. In particular we will fit a distribution to the daily price of crude oil and assess the impact of the annual time specific effects on the monthly mean price of crude oil. We are interested in investigating whether the price shock is interrelated with monthly average price of the crude oil or not. Finally, we shall compare the volatility of the monthly mean price of crude oil and the price shock on crude oil with in the month.
4. The Data and the Variables of the Study
- The study used data obtained from OPEC (http://www.opec.org/opec_web/en/) for the period between 1st Jan 2003 to 31st Dec 2012.The Exogenous Variables are: (1). annual time specific effects (TE): these include overall factors that indicated in section 1.3 that appeared in each year. (2). the sine and cosine waves over time. The Dependent (Endogenous) Variables are: (1).The monthly average price of crude oil (Pr) and (2). The standard deviation on crude oil prices as the price shock on the crude price within the month (Ps)
5. Methodology
- The Galton distribution, also called log-normal distribution is a probability distribution of a random variable whose logarithm is normally distributed. The log normal distribution is given as:
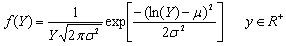 | (1) |
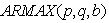 refers to the model with p autoregressive terms, q moving average terms and b exogenous inputs terms. This model contains the
refers to the model with p autoregressive terms, q moving average terms and b exogenous inputs terms. This model contains the 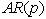 and
and 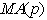 models and a linear amalgamation of the last b terms of exogenous inputs. The ARMAX model is given as (A. Ouakasse and G. Melared, 2009):
models and a linear amalgamation of the last b terms of exogenous inputs. The ARMAX model is given as (A. Ouakasse and G. Melared, 2009): 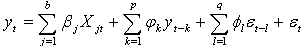 | (2) |
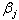 s are the coefficients the exogenous input, and
s are the coefficients the exogenous input, and 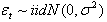 If we assume
If we assume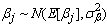 and
and 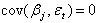 , then equation 2 is written as:
, then equation 2 is written as: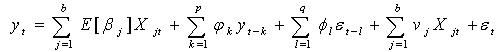 | (3) |
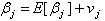 Let
Let 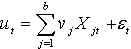 , then equation 3 is written as:
, then equation 3 is written as: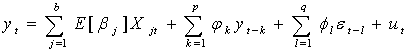 | (4) |
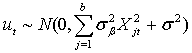 The parameter estimation of ARMAX models in equation 2 and equation 4 with dummy exogenous inputs is based on the Melard’s algorism[20,21]. Finding appropriate values of p and q in the
The parameter estimation of ARMAX models in equation 2 and equation 4 with dummy exogenous inputs is based on the Melard’s algorism[20,21]. Finding appropriate values of p and q in the  model can be facilitated by plotting the partial-autocorrelation functions for determining p, and likewise using the autocorrelation functions for determining q. We will use two different criteria to decide the best order of the model.Akaike Information Criterion (AIC): AIC is a measure of the relative goodness of fit of a statistical model. It is grounded in the concept of information entropy, in effect offering a relative measure of the information lost when a given model is used to describe reality.
model can be facilitated by plotting the partial-autocorrelation functions for determining p, and likewise using the autocorrelation functions for determining q. We will use two different criteria to decide the best order of the model.Akaike Information Criterion (AIC): AIC is a measure of the relative goodness of fit of a statistical model. It is grounded in the concept of information entropy, in effect offering a relative measure of the information lost when a given model is used to describe reality. 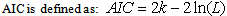 | (5) |
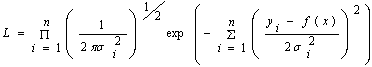 | (6) |
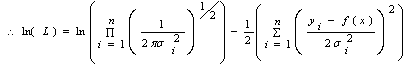 | (7) |
 | (8) |
 | (9) |
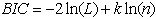 | (10) |
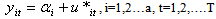 | (11) |
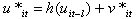 serially correlated random error term,
serially correlated random error term, 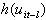 the functional structure of the serial correlation,
the functional structure of the serial correlation, 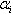 is the ith effect on
is the ith effect on 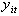 and
and 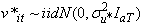 The Cochrane–Orcutt recursive estimation procedure is done by assuming there is first order serial correlation on the random error term
The Cochrane–Orcutt recursive estimation procedure is done by assuming there is first order serial correlation on the random error term 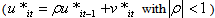 . Then the original model is transformed in to:
. Then the original model is transformed in to: 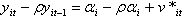 | (12) |
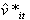 suggests the error terms are dependent, then we continue assuming first order serial correlation on the residuals
suggests the error terms are dependent, then we continue assuming first order serial correlation on the residuals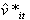 . We continue this recursive process until the estimated residuals are independent[23].
. We continue this recursive process until the estimated residuals are independent[23]. 6. The results
- Econometric Frame Work for Problem Decomposition:
6.1. Assessing the Existence of Specific Probability Distribution of the Daily Prices of Crude oil
- Table 1 summarizes basic properties of the time series for the various years.The sample statistic suggests that measures of central tendency, dispersion, shape and scale are time variant. This shows that the price of the crude oil has its own structure in each fiscal year. From this fact we can conclude that the daily prices of crude oil by annual discretization are not stationary. Moreover, the following Figure 1 confirms our argument. Therefore, this shows that we cannot use the Galton probability distribution nor others are the specific probability distribution of the daily price of crude oil at the international market, in contrast to the conclusion in Haiyan Xu et al[17]. The implications of the absence of specific probability distribution function to the daily price of crude oil to the oil importer nations is strong exertion of scheduling annual budget to import it. In the following analysis we split the variation of the daily price of crude oil into monthly average prices and price shock within the month. This allows assuming a multivariate normal model, thanks to the central limit theorem.
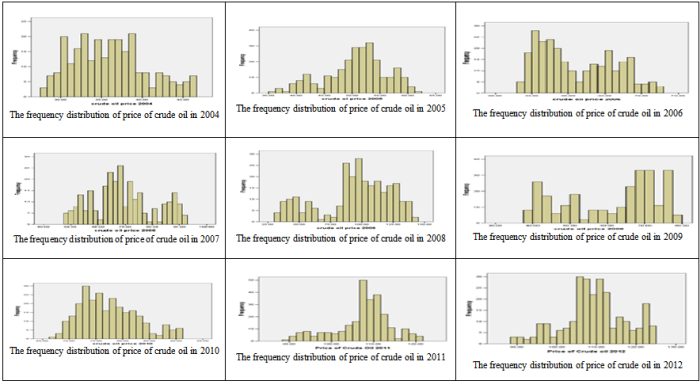 | Figure 1. the frequency distributions of the daily price of crude oil by annual discretization |
|
6.2. Modelling the Monthly Average Price of Crude Oil
- The econometric model that we are going to fit is given as:
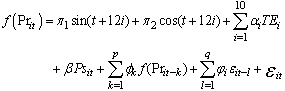 | (13) |
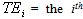 annual time specific effect from 2003-2012 on the price of crude oil, Psit is the price shock on crude oil in the ith year and in the tth month, Prit is the monthly average price of crude oil in ith year and in tth month, The sine and the cosine waves are the harmonic regression components over the yearly cycle,
annual time specific effect from 2003-2012 on the price of crude oil, Psit is the price shock on crude oil in the ith year and in the tth month, Prit is the monthly average price of crude oil in ith year and in tth month, The sine and the cosine waves are the harmonic regression components over the yearly cycle, 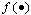 is a mathematical transformation function of Prit and
is a mathematical transformation function of Prit and 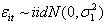 After comparing different ARMAX models, we found that the log-transformed monthly average price of crude oil is best fitted by the
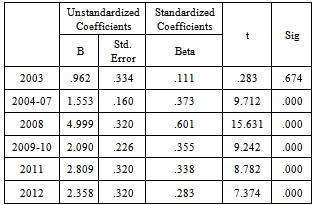
After comparing different ARMAX models, we found that the log-transformed monthly average price of crude oil is best fitted by the 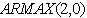 model. Table 2 can give as the estimates of the model parameters. Economic interpretations of the results of Table 2The Log-monthly average price of the crude oil is strongly affected by each of the annual the time specific effects. When we deeply investigate the charactertics of the time specific effects, they are increasing with time (positively correlated with
model. Table 2 can give as the estimates of the model parameters. Economic interpretations of the results of Table 2The Log-monthly average price of the crude oil is strongly affected by each of the annual the time specific effects. When we deeply investigate the charactertics of the time specific effects, they are increasing with time (positively correlated with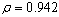 ). This suggests that the future price of crude oil at the international market will be higher than the previous years. From 2003-2006, the US-Iraq war plays a substantial role on the raise of the monthly average price of crude oil (as we see from the table, from 2003-2006 the estimated model parameters of the annual time specific effects are sharply increasing with time). This result argues with research papers like Paul Stevens [4], Lutz Kilian[12] and Haiyan Xu et al[17].In normal conditions of analysis of prices, it is expected that the price shock on the commodity is higher at higher prices of the commodity. However, astonishingly the monthly average price of crude oil and the price shock at the international market are uncorrelated (P-value=0.939). This shows that the increment of the monthly average prices of crude oil can’t explain the increase of the price shock and vice versa.The AR (2) process is the stochastic part is significant to the current monthly average price of crude oil. This implies that the monthly average price of crude oil is dissipated after two month periods. Moreover, the Harmonic part of the regression are all insignificant, this demonstrations that there are no seasonal variations on monthly average price crude oil. From Figure 2 we see a remarkable fit that even it is knotty to differentiate the observed average monthly prices of the crude oil and the predicted values using the model. This showing that first, splitting the variation of the daily price of crude oil into monthly average prices and price shock within the month created a well-structured environment for econometric modelling of crude oil price issues. Second, the fit of the model recommend that we have to include the specific annual time effects whenever forecasting of the monthly average crude oil price is needed. Therefore, unlike other research papers ( like Yu Wei et al[13], Hassan Mohammad and Lixian Su[15], H. Mostafaei and L. Sakhabaksh[16]), it is better to apply the ARMAX models to capture the fluctuations of the monthly average price of crude oil for short memory prediction.
). This suggests that the future price of crude oil at the international market will be higher than the previous years. From 2003-2006, the US-Iraq war plays a substantial role on the raise of the monthly average price of crude oil (as we see from the table, from 2003-2006 the estimated model parameters of the annual time specific effects are sharply increasing with time). This result argues with research papers like Paul Stevens [4], Lutz Kilian[12] and Haiyan Xu et al[17].In normal conditions of analysis of prices, it is expected that the price shock on the commodity is higher at higher prices of the commodity. However, astonishingly the monthly average price of crude oil and the price shock at the international market are uncorrelated (P-value=0.939). This shows that the increment of the monthly average prices of crude oil can’t explain the increase of the price shock and vice versa.The AR (2) process is the stochastic part is significant to the current monthly average price of crude oil. This implies that the monthly average price of crude oil is dissipated after two month periods. Moreover, the Harmonic part of the regression are all insignificant, this demonstrations that there are no seasonal variations on monthly average price crude oil. From Figure 2 we see a remarkable fit that even it is knotty to differentiate the observed average monthly prices of the crude oil and the predicted values using the model. This showing that first, splitting the variation of the daily price of crude oil into monthly average prices and price shock within the month created a well-structured environment for econometric modelling of crude oil price issues. Second, the fit of the model recommend that we have to include the specific annual time effects whenever forecasting of the monthly average crude oil price is needed. Therefore, unlike other research papers ( like Yu Wei et al[13], Hassan Mohammad and Lixian Su[15], H. Mostafaei and L. Sakhabaksh[16]), it is better to apply the ARMAX models to capture the fluctuations of the monthly average price of crude oil for short memory prediction.
|
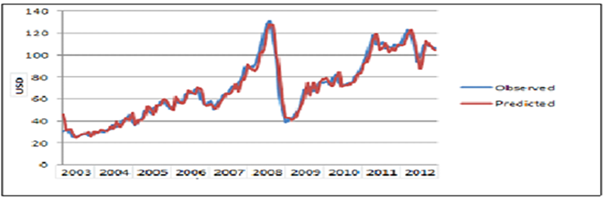 | Figure 2. The comparison of the fitted and observed values of the monthly average price of crude oil using the Log-transformed model |
6.3. Developing the best fit of the fluctuations of the price shock on Crude Oil
- Let us now consider a model for the time serioes of the shock prices only. The model which can capture the fluctuations of price shock on crude oil is given as:
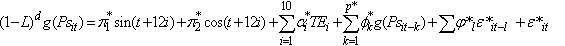 | (14) |
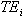 is the ith annual time specific effect from 2003-2011 on the price of crude oil, Psit is the price shock on crude oil in ith year and in tth month, The sine and the cosine waves are the harmonic regression components, d is the appropriate differencing operator
is the ith annual time specific effect from 2003-2011 on the price of crude oil, Psit is the price shock on crude oil in ith year and in tth month, The sine and the cosine waves are the harmonic regression components, d is the appropriate differencing operator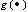 is a mathematical transformation function of Psit and
is a mathematical transformation function of Psit and 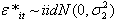 After comparing different models, we found that the
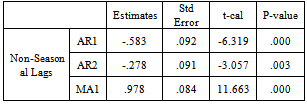
After comparing different models, we found that the 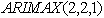 model is the best fit for the price shock on crude oil. Table 3 gives as the estimates of the model parameters.
model is the best fit for the price shock on crude oil. Table 3 gives as the estimates of the model parameters.
|
6.4. Comparisons on the Amplitudes of Price Shock on Crude Oil
- In this section we try to compare the price shocks on crude oil by categorizing annual times that have similar amplitude of disturbances and using the autoregression. Table 4 can give us the estimated price shock recorded with in the category of time fixed effects using the Cochrane-Orcutt recursive estimation method.
|
7. Conclusions and Recommendations
7.1. Conclusions
- This paper tried to see whether the daily prices of crude oil by annual discretization follows a specific probability distribution or not. Based up on the time variant property of the important sample statistic as the estimates of the population parameters, we conclude that there is no specific probability distribution for the daily price of crude oil by annual discretization. using discrete dynamic stochastic models on the newly introduced variables by splitting the variations of the daily prices of crude oil into monthly average price and price shock within the month, the paper found that the
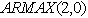 model capture the monthly price of crude oil and the
model capture the monthly price of crude oil and the 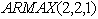 stochastic model capture the amplitude of price shock on crude oil. A noteworthy result that the paper identified is that the source of price shock is not correlated (P-value=0.939) with the monthly average price of the crude oil. Moreover, the time specific effects are uncorrelated with the price shock on crude oil.
stochastic model capture the amplitude of price shock on crude oil. A noteworthy result that the paper identified is that the source of price shock is not correlated (P-value=0.939) with the monthly average price of the crude oil. Moreover, the time specific effects are uncorrelated with the price shock on crude oil. 7.2. Recommendations
- The price of crude oil in the international market is complete of stochastic type. This randomness is most likely being complicated as the world’s economic integration is more globalized. This problem of has two major consequences on the oil-importer nations. If the economy the oil importer nation is strong, then they will rebalance their expenditure for oil by their revenue from export. In this case, either if the price of oil is increasing or not, the structure of the increment of the price of crude oil will most probably not affect the economy of the oil-importer nation. On the other hand, if the economy of the oil-importer nation is weak, then the nation’s expenditure of importing oil is most likely unbalanced by the revenue of the nation’s export. From this point of view, the raise of the price of crude oil in the international market most likely affects the economy of oil importer developing nations. Therefore, especially oil-importer developing nations need to have the implementations of other energy sources like hydro-electric power, bio-fuel, solar energy, wind energy or others. From the structural trend of the composition of the world’s sources of energy, the energy source from oil is the leading in these recent times. Obviously, this high demand of oil in the world energy market cause to fluctuate its prices. Therefore, each nation in the world should focus on the strategies how to increase the share of the other energy sources and how to properly use them. Once the share of crude oil is decreasing, its price and its price shock will be stabilized. In this regard, the role technologically advanced nations is much significant.
ACKNOWLEDGEMENTS
- I have my deepest thank to my God who gave me time and space. My existence is meaningful whenever I respect and follow the rule of his 10-commandnents. Next, I want to say to my mother Birhan Endalew, “My mother, I appreciate your endurance and strength. Moreover, whenever I am wherever I go your spirit is following and supporting me”.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
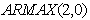 model
model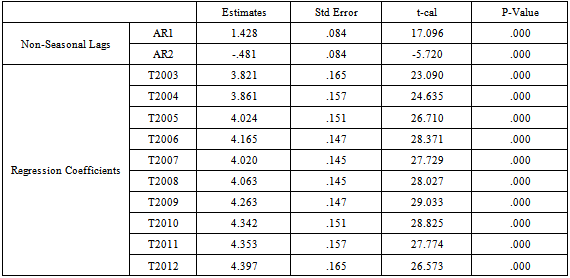
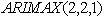 model:
model: