1. Introduction

The assumptions of Cournot and Stackelberg behavior have been widely used in analyzing quantity-setting oligopoly games. The Cournot game involves simultaneous moves, while the Stackelberg game involves sequential moves. In general, it is well known that the profit-maximizing Stackelberg leader can get a higher profit than the follower by committing to a high quantity. A number of recent papers consider models that endogenously determine the roles of the leader and follower. In a much-cited paper, Hamilton and Slutsky[1] examine the novel issue of endogenous timing in two-player games, with important modeling implications for several models in industrial economics. In a preplay stage, players decide whether to choose actions in the basic game at the first opportunity or to wait until observing their rivals’ first period actions. In one extended game, players first decide when to choose actions without committing to actions in the basic game. The equilibrium has a simultaneous play subgame unless payoffs in a sequential play subgame Pareto dominate those payoffs. In another extended game, deciding to choose at the first turn requires committing to an action. They show that both sequential play outcomes are the equilibria only in undominated strategies. Amir[2] relates to the study of[1] on endogenous timing (with observable delay). He shows, via counterexample, that monotonicity of the best-response functions in a two-player game is not sufficient to derive predictions about the order of moves and this requires, additionally, the monotonicity of each payoff in the other player’s actions. There are many further studies, such as[3-11]. However, these studies are models with profit- maximizing capitalist firms and do not include state-owned firms.

Some studies analyze endogenous timing in mixed market models that include state-owned public firms.¹ For example, Pal[18] addresses the issue of endogenous order of moves in a mixed market by adopting the observable delay game of[1] in the context of a quantity-setting mixed market where state-owned and capitalist firms first choose the timing of choosing their quantities, and shows the results are strikingly different from those obtained in a corresponding quantity-setting market with all profit-maximizing capitalist firms. Matsumura[19] examines an international mixed duopoly model where a domestic state-owned firm and a foreign profit-maximizing firm first choose the timing for choosing their quantities and shows that, in contrast to[18] discussing a case of domestic competitors, the state-owned firm should be the leader. Lu[20] examines endogenous timing in a mixed oligopoly consisting of a single state-owned firm and foreign profit-maximizing competitors and shows that the results are the same in two cases: (i) there are only two time periods for quantity choice, and (ii) there are more than two time periods for quantity choice and there are more than two profit-maximizing firms. Bárcena-Ruiz[21] considers a mixed duopoly in which a state-owned firm and a profit-maximizing firm choose whether to set prices sequentially and simultaneously and shows that they choose prices simultaneously. He finds that the result obtained in the mixed duopoly under price competition differs from the one under quantity competition. In addition, Lu and Poddar[22] examine a two-stage game of endogenous timing with observable delay in the context of sequential capacity and quantity choice, and show that in mixed duopoly the state-owned and the profit-maximizing firm choose capacity and quantity sequentially in all possible equilibria and no simultaneous capacity or quantity choice case can be a part of equilibrium. However, these studies are models with state-owned and capitalist firms and do not include labor-managed firms.

Therefore, we investigate an endogenous role in a mixed duopoly where a state-owned firm competes with a labor-managed firm.² Lambertini[28] investigates a mixed duopoly where a profit-maximizing and a labor-managed firm compete either in prices or in quantities, and shows that if firms can choose the timing of moves before competing in the relevant market variable, the Bertrand game yields multiple equilibria, while the Cournot game has a unique subgame perfect equilibrium with the profit-maximizing firm in the leader’s role and the labor-managed firm in the follower’s role. In addition, Ohnishi[29] considers an endogenous-timing mixed model in which a state-owned firm competes against a foreign profit-maximizing firm and shows that the foreign profit-maximizing firm does not always choose following. Lambertini[28] studies mixed market competition with profit-maximizing and labor-managed firms, and Ohnishi[29] considers mixed market competition with state-owned and foreign profit-maximizing firms. On the other hand, we investigate mixed market competition consisting of state-owned and labor-managed firms.

We examine a model in which a state-owned firm competes with a labor-managed firm. We consider the following situation. There are two production stages, and both firms first announce in which stage they will choose output. Next, if both firms decide to choose output in the same stage, a simultaneous move game occurs, whereas if both firms decide to choose output in different stages, a sequential move game arises. We discuss the equilibrium of the endogenous timing model. As the result of this analysis, we find that the state-owned firm cannot play the role of the leader.

The remainder of this paper is organized as follows. In Section 2, we describe the model. Section 3 gives supplementary explanations of the model. Section 4 presents the equilibrium of the model. Finally, Section 5 concludes the paper.

2. The Model

Let us consider a market with one state-owned firm (firm 1) and one labor-managed firm (firm 2), producing a single homogeneous good. In the remainder of this paper, subscripts 1 and 2 denote firm 1 and firm 2, respectively. In addition, when 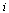and 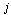are used to refer to firms in an expression, they should be understand to refer to 1 and 2 with 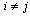. The market price is determined by the inverse demand function 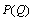, where 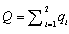. We assume that 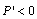and .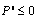

Social welfare, which is the sum of consumers’ surplus and total profits by the firms, is given by

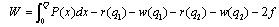(1)

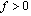where denotes the capital cost function, is the labor cost function, and is the fixed cost. We assume 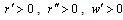and 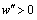.³ Firm 1 chooses 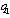in order to maximize (1).

Firm 2’s income per worker is given by

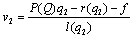(2)

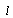where denotes the labor input function. We assume that 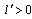and 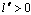. Firm 2 chooses 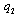in order to maximize (2).

The timing of the game is as follows. In stage 1, each firm simultaneously and independently chooses 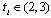, where 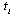indicates when to decide the non-negative output 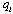. That is, 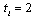implies that firm produces in stage 2, and 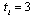implies that it produces in stage 3. At the end of stage 1, each firm observes 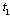and 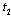. In stage 2, firm 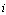choosing 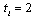selects its output in this stage. In stage 3, firm 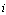choosing 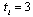selects its output 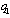in this stage. At the end of the game, the market opens and each firm sells its output 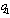. In this paper, we use subgame perfection as the equilibrium concept. In our discussion, we assume that both social welfare and firm 2’s income per worker are positive.

3. Supplementary Explanations

First, we derive firm 1’s reaction function in quantities. The equilibrium occurs where firm 1 maximizes social welfare with respect to its own output level, given the output level of firm 2. Therefore, firm 1’s reaction function is defined by

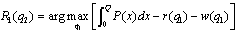(3)

We now state the following lemma.

Lemma 1. Under Cournot competition, is downward sloping.

Proof. Firm 1 aims to maximize social welfare with respect to its own output, given firm 2’s output. The equilibrium must satisfy the following conditions: The first-order condition for firm 1 is

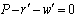(4)

and the second-order condition is

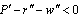(5)

Furthermore, we have

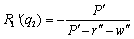(6)

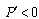Since , Lemma 1 follows. Q.E.D.

Second, we derive firm 2’s reaction function in quantities. The equilibrium occurs where firm 2 maximizes its income per worker with respect to its own output level, given the output level of firm 1. Firm 2’s reaction function is defined by

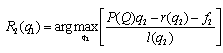(7)

We present the following lemma.

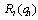Lemma 2. Under Cournot competition, is upward sloping.

Proof. Firm 2 aims to maximize its income per worker with respect to its own output level, given firm 1’s output. The equilibrium must satisfy the following conditions: The first-order condition for firm 2 is

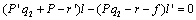(8)

and the second-order condition is

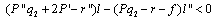(9)

Furthermore, we have

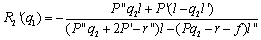(10)

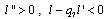Since, so that 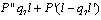is positive. Q.E.D.

Third, we consider Stackelberg games. If firm 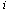is the Stackelberg leader, then firm 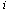selects 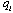, and firm selects 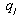after observing 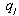. Firm 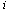maximizes 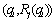with respect to 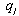. We present the following lemma, where the superscripts 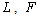and 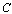denote the Stackelberg equilibrium outcome where firm 1 is the leader, the Stackelberg equilibrium outcome where firm 1 is the follower, and the Cournot equilibrium outcome, respectively.

Lemma 3. (i) 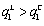, (ii) 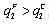, (iii) 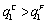, and (iv) .

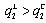Proof. (i) If firm 1 is the Stackelberg leader, then it maximizes 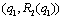with respect to 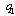. Therefore, firm 1’s Stackelberg leader output satisfies the first-order condition:

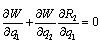(11)

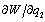Here, is positive, and 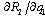is also positive by Lemma 2. To satisfy (11), 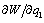must be negative.

(ii) If firm 2 is the Stackelberg leader, then it maximizes 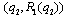with respect to 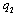. Therefore, firm 2’s Stackelberg leader output satisfies the first-order condition:

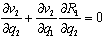(12)

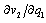Here, is negative, and 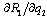is also negative by Lemma 1. To satisfy (12), 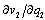must be negative.

(iii) This follows from Lemma 1 and Lemma 3 (ii).

(iv) This follows from Lemma 2 and Lemma 3 (i). Q.E.D.

Lemma 3 indicates that each firm has an incentive to increase its output.

4. Equilibrium

Before discussing the equilibrium outcome in the endogenous timing game, we present the following two propositions.

Proposition 1. (i) 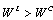and (ii) .

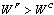Proof. (i) If firm 1 is the Stackelberg leader, then it maximizes social welfare with respect to 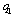. Since firm 1 can choose 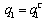, we obtain 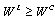. Proposition 1 (i) follows from Lemma 3 (i).

(ii) Consider the game where firm 1 is the follower and firm 2 is the leader. Lemma 3 (iv) shows 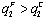. Since 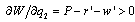, increasing 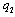increases social welfare, and thus Proposition 1 (ii) follows. Q.E.D.

The intuition behind Proposion 1 is straightforward. Since firm 1 aims to maximizes social welfare, it is clear that 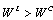, and we can easily guess that Proposition 1 (i) holds. Next, if firm 2 is the leader, then it increases its output, and hence social welfare increases. Proposition 1 (ii) means that firm 1 has the follower’s advantage.

Proposition 2. (i) 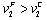and (ii) .

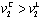Proof. (i) If firm 2 is the Stackelberg leader, then it maximizes its income per worker with respect to 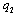. Since firm 2 can choose 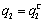, we obtain 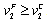. Furthermore, Proposition 2 (i) follows from Lemma 3 (ii).

(ii) Consider the game where firm 1 is the leader and firm 2 is the follower. Lemma 3 (i) shows 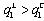. Since 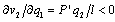, increasing 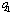decreases 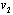. Q.E.D.

Proposition 2 indicates that firm 2 should be the leader. Since firm 2 aim to maximize its income per worker, it is clear that 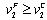, and we can easily guess that the strict inequality holds. The intuition behind Proposition 2 (ii) is also straightforward. If firm 1 is the leader, then it increases 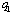. Increasing 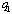decreases 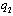because of perfect substitute goods, and moreover decreasing 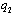decreases .

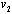We now present the subgame perfect equilibrium of the endogenous timing game described in Section 2. The main result of this study is stated in the following proposition.

Proposition 3. In the unique equilibrium 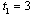and .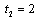

Proof. In stage 1, each firm simultaneously and independently chooses 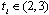. At the end of stage 1, each firm observes 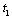and 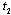. In stage 2, firm 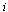choosing 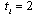selects its output 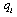in this stage. In stage 3, firm 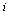choosing 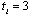selects its output 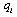in this stage. At the end of the game, the market opens and each firm sells its output 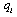. Hence, we can consider the following matrix:

From the previous propositions, we know that 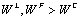and 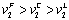. Thus, the equilibrium occurs at “stage 3” for firm 1 and “stage 2” for firm 2. Q.E.D.

This proposition indicates that in the unique equilibrium firm 1 (the state-owned firm) cannot play the role of Stackelberg leader. The intuition behind Proposition 3 is as follows. First, we consider the strategy of firm 2. Suppose that firm 2 chooses 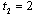. If firm 1 chooses 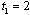, then the outcome becomes 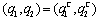. If firm 1 chooses 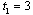, then the outcome becomes 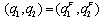. Suppose that firm 2 chooses 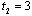. If firm 1 chooses 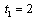, then the outcome becomes 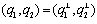. If firm 1 chooses 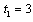, then the outcome becomes 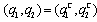. Proposition 3 shows that 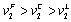. Thus, firm 2 always chooses 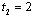irrespective of the choice of firm 1.

Next, we consider the strategy of firm 1. Our equilibrium concept is subgame perfection and all information in the model is common knowledge. Firm 1 knows that firm 2 chooses 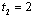. If firm 1 chooses 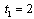, then the outcome becomes 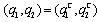. If firm 1 chooses 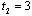, then the outcome becomes 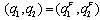. Proposition 1 shows that 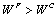. Hence, firm 1 chooses .

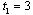5. Conclusions

We have considered a quantity-setting model in which a state-owned firm competes with a labor-managed firm. We have shown that the unique equilibrium coincides with the Stackelberg solution in which the labor-managed firm is the leader. As the result of the analysis, we have found that the state-owned firm cannot play the role of Stackelberg leader. Diverse extensions of this study will be considered in the near future.

Notes

1. The pioneering work of state-owned public firms was done by [12]. See also, for example, [13-17] for excellent surveys.

2. The first work on a theoretical model of a labor-managed firm was conducted by [23]. Seealso, for example, [24-27] for excellent surveys.

3. We assume that both firms share the same cost function and the marginal cost is increasing. This assumption is often used in literature studying mixed markets. See, for example, [30-41]. If the marginal cost is constant or decreasing, then firm 1 (the state-owned firm) produces an output such that price equals marginal cost and supplies the entire market, resulting in a welfare-maximizing public mo-nopoly. This assumption is made to eliminate such a trivial solution.