-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Economics
p-ISSN: 2166-4951 e-ISSN: 2166-496X
2012; 2(1): 53-56
doi:10.5923/j.economics.20120201.07
A Two-Stage Quantity-Setting Duopoly: Cournot or Stackelberg
Kazuhiro Ohnishi
Institute for Basic Economic Science, Japan
Correspondence to: Kazuhiro Ohnishi, Institute for Basic Economic Science, Japan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper considers a two-stage quantity-setting duopoly model. In the first stage, each firm independently announces its output. Each firm can discount its announced output but cannot raise it. In the second stage, each firm independently chooses its actual output. The paper classifies demand functions into the following four cases in terms of the goods relevance and strategic relevance between both firms: “substitute goods and strategic substitutes”, “substitute goods and strategic complements”, “complementary goods and strategic substitutes” and “complementary goods and strategic complements”. The paper presents the subgame perfect Nash equilibrium in each of four cases.
Keywords: Two-Stage Model, Cournot Equilibrium, Stackelberg Equilibrium
Cite this paper: Kazuhiro Ohnishi, A Two-Stage Quantity-Setting Duopoly: Cournot or Stackelberg, American Journal of Economics, Vol. 2 No. 1, 2012, pp. 53-56. doi: 10.5923/j.economics.20120201.07.
Article Outline
1. Introduction
- The analysis of [3] considers a two-stage price-setting duopoly model.1 The two stages are as follows. In the first stage, each firm simultaneously and independently announces its price. The firms cannot raise their announced prices, but can discount them. At the end of the first stage, each firm knows its rival firm’s price. In the second stage, each firm simultaneously and independently chooses its actual price. At the end of the second stage, the market opens. He classifies demand functions into the following four cases in terms of the goods relevance and strategic relevance between both firms: “substitute goods and strategic complements”, “substitute goods and strategic substitutes”, “complementary goods and strategic complements” and “complementary goods and strategic substitutes”. He demonstrates that the subgame perfect Nash equilibrium outcomes depend on the properties of each firm’s demand function, and therefore, there are three patterns of equilibrium outcomes: Bertrand equilibrium only, Stackelberg equilibrium only, and both equilibria.We examine a two-stage quantity-setting duopoly model. We also classify demand functions into four cases in terms of the goods relevance and strategic relevance between both firms: “substitute goods and strategic substitutes”, “substitute goods and strategic complements”, “complementary goods and strategic substitutes”, and “complementary goodsand strategic complements”. We present the subgame perfect Nash equilibrium in each of four cases by using the two- stage quantity-setting model.The remainder of this paper is organized as follows. In Section 2, we describe the model. Section 3 gives supplementary explanations of the model. Section 4 discusses the equilibrium of the model. Section 5 concludes the paper.
2. The Model
- In this section, we describe a two-stage quantity-setting game. There are two firms: firm 1 and firm 2. In the remainder of this paper, subscripts 1 and 2 denote firm 1 and firm 2, respectively. In addition, when
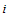 and
and 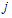 are used, they should be understood to refer to 1 and 2 with
are used, they should be understood to refer to 1 and 2 with  There is no possibility of entry or exit. The two stages of the game are as follows. In the first stage, each firm
There is no possibility of entry or exit. The two stages of the game are as follows. In the first stage, each firm 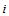 simultaneously and independently announces its output
simultaneously and independently announces its output 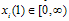 . At the end of the first stage, each firm knows
. At the end of the first stage, each firm knows 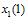 and
and 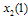 . In the second stage, each firm
. In the second stage, each firm 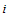 simultaneously and independently chooses its actual output
simultaneously and independently chooses its actual output 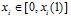 . At the end of the second stage, the market opens and each firm sells its actual output xi .Firm
. At the end of the second stage, the market opens and each firm sells its actual output xi .Firm 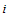 ’s profit is
’s profit is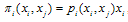 | (1) |
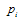 is twice continuously differentiable with
is twice continuously differentiable with 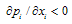 (downward-sloping demand).This assumption ensures a smooth demand function. Throughout the paper, we use subgame perfection as our equilibrium concept and restrict our attention to pure strategy equilibria.
(downward-sloping demand).This assumption ensures a smooth demand function. Throughout the paper, we use subgame perfection as our equilibrium concept and restrict our attention to pure strategy equilibria.3. Supplementary Explanations
- First, we describe the Cournot equilibrium in quantities.Definition 1. Firm
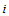 ’s reaction function is defined by
’s reaction function is defined by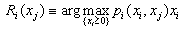 .Definition 2. The Cournot equilibrium is defined as a pair
.Definition 2. The Cournot equilibrium is defined as a pair  of output levels, where
of output levels, where 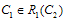 and
and 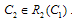 The outputs
The outputs 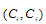 of the Cournot equilibrium satisfy the following conditions: The first-order conditions for profit maximization is
of the Cournot equilibrium satisfy the following conditions: The first-order conditions for profit maximization is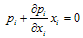 | (2) |
 | (3) |
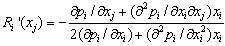 | (4) |
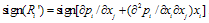 . Therefore, if
. Therefore, if 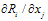 is negative (respectively positive), firm i’s reaction curve is downward-sloping (respectively upward-sloping) and strategies are strategic substitutes (respectively complements).2 We make the following assumption.Assumption 2. If
is negative (respectively positive), firm i’s reaction curve is downward-sloping (respectively upward-sloping) and strategies are strategic substitutes (respectively complements).2 We make the following assumption.Assumption 2. If 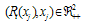 , then
, then 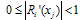 (stability condition).Assumption 2 is a stability condition and guarantees the uniqueness of the Cournot equilibrium for the standard adjustment mechanism. That is,
(stability condition).Assumption 2 is a stability condition and guarantees the uniqueness of the Cournot equilibrium for the standard adjustment mechanism. That is,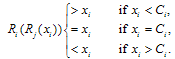 | (5) |
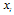 and firm j chooses
and firm j chooses 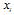 after observing
after observing 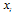 . Given
. Given 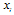 , firm i maximizes its profit
, firm i maximizes its profit 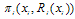 with respect to
with respect to 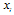 . The first-order condition for profit maximization is
. The first-order condition for profit maximization is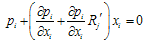 | (6) |
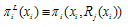 Definition 4. The Stackelberg equilibrium is defined by
Definition 4. The Stackelberg equilibrium is defined by 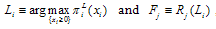 , where
, where 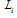 is the Stackelberg leader’s output and
is the Stackelberg leader’s output and 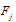 is the Stackelberg follower’s output.
is the Stackelberg follower’s output.4. Equilibrium Outcomes
- In this section, we discuss the equilibrium outcomes of the two-stage quantity-setting model formulated in Section 2. We consider the following four cases.3Case 1:
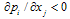 and
and 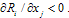 .Case 2:
.Case 2: 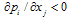 and
and 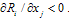 .Case 3:
.Case 3: 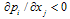 and
and 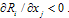 .Case 4:
.Case 4: 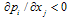 and
and 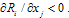 .Case 1 is the case considered by standard Cournot competition. We now discuss these cases.Cases 1 and 4Case 1 is the case of strategic substitutes in which goods are substitutes. Case 4 is the case of strategic complements in which goods are complements. The equilibrium outcome of these two cases is stated by the following proposition,Proposition 1. Suppose that Assumptions 1-3 are satisfied. If
.Case 1 is the case considered by standard Cournot competition. We now discuss these cases.Cases 1 and 4Case 1 is the case of strategic substitutes in which goods are substitutes. Case 4 is the case of strategic complements in which goods are complements. The equilibrium outcome of these two cases is stated by the following proposition,Proposition 1. Suppose that Assumptions 1-3 are satisfied. If 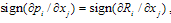 , then the set of equilibrium outcomes
, then the set of equilibrium outcomes 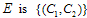 The intuition behind Proposition 1 is as follows. First, we illustrate Case 1, which is drawn in Figure 1.
The intuition behind Proposition 1 is as follows. First, we illustrate Case 1, which is drawn in Figure 1. 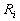 is firm i’s reaction curve, and
is firm i’s reaction curve, and 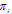 is firm i’s isoprofit contour. In Case 1, firm i’s reaction curves are downward-sloping because of strategic substitutes. Firm i’s profit increases (respectively decreases) with the fall (respectively rise) of firm j’s output on firm i’s reaction curve. In Figure 1, the Stackelberg point
is firm i’s isoprofit contour. In Case 1, firm i’s reaction curves are downward-sloping because of strategic substitutes. Firm i’s profit increases (respectively decreases) with the fall (respectively rise) of firm j’s output on firm i’s reaction curve. In Figure 1, the Stackelberg point 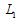 where firm 1 is the leader and firm 2 is the follower is to the right of
where firm 1 is the leader and firm 2 is the follower is to the right of 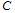 on the curve
on the curve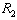 . That is, each firm’s Stackelberg leader output exceeds its Cournot output. Firm 1’s profit is the highest at
. That is, each firm’s Stackelberg leader output exceeds its Cournot output. Firm 1’s profit is the highest at 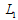 on
on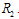 . The further the point on
. The further the point on 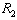 gets from the Stackelberg point
gets from the Stackelberg point 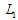 , the more firm 1’s profit decreases. Therefore, firm 1 wants to commit itself to a larger output in the first stage. However, since firm 1 can discount its stated output
, the more firm 1’s profit decreases. Therefore, firm 1 wants to commit itself to a larger output in the first stage. However, since firm 1 can discount its stated output 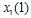 , this commitment is not credible. Since the game is symmetric, firm 2’s incentives are the same, and hence the equilibrium is at point
, this commitment is not credible. Since the game is symmetric, firm 2’s incentives are the same, and hence the equilibrium is at point 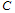 in Figure 1.Next, we illustrate Case 4, which is drawn in Figure 2. In Case 4, firm i’s reaction curves are upward-sloping because of strategic complements. Firm i’s profit increases (respectively decreases) with the rise (respectively fall) of firm j’s output on firm i’s reaction curve. The Stackelberg point
in Figure 1.Next, we illustrate Case 4, which is drawn in Figure 2. In Case 4, firm i’s reaction curves are upward-sloping because of strategic complements. Firm i’s profit increases (respectively decreases) with the rise (respectively fall) of firm j’s output on firm i’s reaction curve. The Stackelberg point 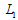 where firm 1 is the leader and firm 2 is the follower is to the right of
where firm 1 is the leader and firm 2 is the follower is to the right of 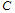 on
on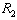 . Firm 1’s profit is the highest at
. Firm 1’s profit is the highest at 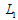 on
on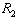 . Therefore, firm 1 wants to commit itself to a larger output in the first stage. However, since firm 1 can discount its stated output
. Therefore, firm 1 wants to commit itself to a larger output in the first stage. However, since firm 1 can discount its stated output 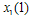 , this commitment is not credible. Since the game is symmetric, firm 2’s incentives are the same. As a result, the equilibrium occurs at
, this commitment is not credible. Since the game is symmetric, firm 2’s incentives are the same. As a result, the equilibrium occurs at 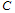 in Figure 2.
in Figure 2.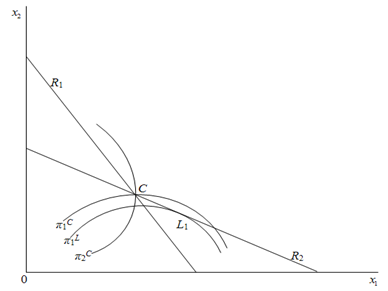 | Figure 1. Case 1: Substitute goods and strategic substitutes |
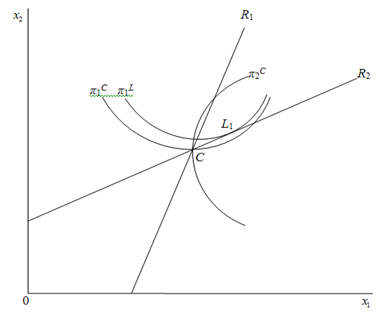 | Figure 2. Case 4: Complementary goods and strategic complements |
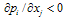 and
and 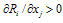 , then
, then 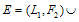
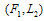 .The intuition behind Proposition 2 is straightforward. Case 2 is illustrated in Figure 3. In Case 2, firm i’s reaction curves are upward-sloping because of strategic complements. Firm i’s profit increases (respectively decreases) with the fall (respectively rise) of firm j’s output on firm i ’s reaction curve. In Figure 3, the Stackelberg point
.The intuition behind Proposition 2 is straightforward. Case 2 is illustrated in Figure 3. In Case 2, firm i’s reaction curves are upward-sloping because of strategic complements. Firm i’s profit increases (respectively decreases) with the fall (respectively rise) of firm j’s output on firm i ’s reaction curve. In Figure 3, the Stackelberg point 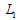 where firm 1 is the leader and firm 2 is the follower is to the left of
where firm 1 is the leader and firm 2 is the follower is to the left of 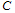 on
on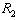 . That is, each firm’s Stackelberg leader output is smaller than its Cournot output. Firm 1’s profit is the highest at
. That is, each firm’s Stackelberg leader output is smaller than its Cournot output. Firm 1’s profit is the highest at 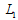 on
on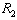 . Decreasing firm i’s output decreases firm j’s output because of strategic complements and furthermore increases each firm’s profit because of complementary goods and strategic complements. Firm 1 has an incentive to cut firm 2’s output and wants to commit itself to a smaller output in the first stage. Since firm 1 can discount its announced output but cannot raise it, this commitment is credible. In our model, firm 1 is able to commit itself to a smaller output. Since the game is symmetric, firm 2’s incentives are the same, and hence the equilibrium is
. Decreasing firm i’s output decreases firm j’s output because of strategic complements and furthermore increases each firm’s profit because of complementary goods and strategic complements. Firm 1 has an incentive to cut firm 2’s output and wants to commit itself to a smaller output in the first stage. Since firm 1 can discount its announced output but cannot raise it, this commitment is credible. In our model, firm 1 is able to commit itself to a smaller output. Since the game is symmetric, firm 2’s incentives are the same, and hence the equilibrium is 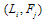 .
.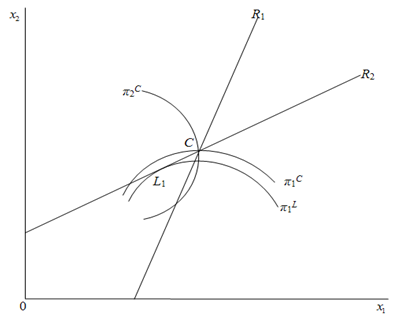 | Figure 3. Case 2: Substitute goods and strategic complements |
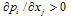 and
and 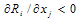 , then
, then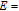
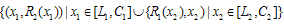 .The intuition behind Proposition 3 is illustrated in Figure 4. In Case 3, firm i’s reaction curves are downward-sloping because of strategic substitutes. Firm i’s profit increases (respectively decreases) with the rise (respectively fall) of firm j’s output on firm i’s reaction curve. The Stackelberg point
.The intuition behind Proposition 3 is illustrated in Figure 4. In Case 3, firm i’s reaction curves are downward-sloping because of strategic substitutes. Firm i’s profit increases (respectively decreases) with the rise (respectively fall) of firm j’s output on firm i’s reaction curve. The Stackelberg point 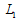 where firm 1 is the leader and firm 2 is the follower is to the left of
where firm 1 is the leader and firm 2 is the follower is to the left of 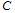 on
on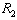 . Firm 1’s profit is the highest at
. Firm 1’s profit is the highest at 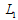 on
on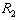 . Decreasing firm i’s output increases firm j’s output because of strategic substitutes and furthermore increases firm 1’s profit because of complementary goods and strategic substitutes. Firm 1 wants to commit itself to a smaller output in the first stage. Since firm 1 can discount its announced output but cannot raise it, this commitment is credible. Firm 1 is able to commit itself to a smaller output, and hence the Stackelberg outcome appears.
. Decreasing firm i’s output increases firm j’s output because of strategic substitutes and furthermore increases firm 1’s profit because of complementary goods and strategic substitutes. Firm 1 wants to commit itself to a smaller output in the first stage. Since firm 1 can discount its announced output but cannot raise it, this commitment is credible. Firm 1 is able to commit itself to a smaller output, and hence the Stackelberg outcome appears.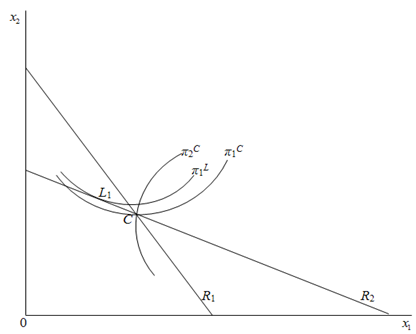 | Figure 4. Case 3: Complementary goods and strategic substitutes |
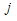 chooses
chooses 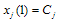 . Then firm i cannot induce a smaller output than
. Then firm i cannot induce a smaller output than 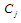 from firm j , and therefore firm i loses the incentive to announce a smaller output like
from firm j , and therefore firm i loses the incentive to announce a smaller output like 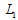 . Hence the Cournot outcome appears in equilibrium.The proofs of Propositions 1-3 are the same as those of Propositions 1-3 in [3] and will be omitted.
. Hence the Cournot outcome appears in equilibrium.The proofs of Propositions 1-3 are the same as those of Propositions 1-3 in [3] and will be omitted.5. Conclusions
- We have classified the demand functions into the four cases in terms of the goods relevance and strategic relevance between two firms and have examined the equilibrium outcome in each of four cases by using a two-stage quantity-setting model. We have shown that the equilibrium outcomes depend crucially on the properties of the demand functions and there are three patterns of equilibrium outcomes: Cournot equilibrium only, Stackelberg equilibrium only, and both equilibria. We have found that our results are the same as those of two-stage price-setting duopoly competition.
Notes
- 1. See Gilbert [2], Shapiro [6] and Tirole [7] for excellent surveys of oligopoly models.2. The concepts of strategic substitutes and complements were introduced by Bulow, Geanakoplos, and Klemperer [1].3. For price competition, see Matsumura [3] and Ohnishi [4]. See also Ohnishi [5].
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML