-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2021; 11(1): 1-8
doi:10.5923/j.control.20211101.01
Received: Aug. 9, 2021; Accepted: Aug. 25, 2021; Published: Sep. 15, 2021

Stochastic Dynamic Systems’ State Estimation Based on Mean Squared Error Minimizing and Kalman Filtering
Bukhar Kussainov
Institute of Heat Power Engineering and Control Systems, Almaty University of Power Engineering and Telecommunications, Almaty, Republic of Kazakhstan
Correspondence to: Bukhar Kussainov, Institute of Heat Power Engineering and Control Systems, Almaty University of Power Engineering and Telecommunications, Almaty, Republic of Kazakhstan.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In automatic control systems, telecommunications and information systems subjected to impact of random disturbances and measurement inaccuracies, there is the problem of estimating the state vector of observed stochastic system. With the aim to solve the problem the state space system model is described and the problem statement is given. To solve the problem it’s used the discrete Kalman filter (KF) presenting itself the recurrent procedure in the form of the set of the difference vector-matrix equations. In the paper the way of deriving the equations of KF on the basis of the procedure of minimization of the mean-squared error of estimation based on a method of the least squares is considered. Using this procedure the discrete analog of the Wiener-Hopf equation as well as Gaussian and Gaussian-Markov estimates of the state vector of linear stochastic system are received satisfying to a minimum of the mean-squared error in the estimate. On the basis of the received estimates and the discrete equation of Wiener-Hopf the equations of the KF is derived, the theorem of the KF with the minimum mean-squared error is formulated, the sequence of using the equations of KF making up the recursive algorithm of KF for computer program realization is explained.
Keywords: Stochastic systems, State estimation, Kalman filter
Cite this paper: Bukhar Kussainov, Stochastic Dynamic Systems’ State Estimation Based on Mean Squared Error Minimizing and Kalman Filtering, International Journal of Control Science and Engineering, Vol. 11 No. 1, 2021, pp. 1-8. doi: 10.5923/j.control.20211101.01.
Article Outline
1. Introduction
- Modern automatic control systems as well as telecommunications and information systems transmitting and processing signals and subjected to impact of random perturbations and uncertainties of system parameters and to influence of random external disturbances and measurement noises can be considered in the form of the state space models of non-stationary linear dynamical stochastic systems [1]. In stochastic systems, to realize modern control algorithms or to separate a useful signal from its mixture with noise, there is a problem of estimating the entire state vector of the dynamical system based on measured values of system’s output signal [2]. The solution of this problem in real time is a filtering problem, for which the classical and most popular solution algorithm is the discrete Kalman filter (KF) [3,4], using both in control theory and in the theory of signal transmission and processing [5]. The KF has the same structure as the considered dynamical system, is the mathematical model and consists of a set of difference vector-matrix equations for calculating estimates of the state of a stochastic system, estimates of the error covariance matrices and the filter gain. The difference between it and the system is that at any given time, the filter gain is optimal relative to the specified statistical properties of disturbances and measurement errors [2-8]. The computational algorithm of the KF is a recursive procedure that is convenient for program realization using programming languages as well as MATLAB [3,9-11] and other computer programs for system modeling.The article presents a mathematical model of a discrete non-stationary linear stochastic dynamical system, the formulation of the problem of estimating the vector of the system state, the derivation of equations and the formulation of the KF theorem, as well as an algorithm for using the equations of the discrete KF. As it’s known, the estimation of the state of a dynamical system (the solution of the filtration problem), as well as the derivation of the KF equations can be carried out using the Bayesian approach, maximum likelihood estimation or the least squares method [12]. Here we follow the already known path and consider the filtration problem as a generalization of the Gaussian least squares method, described in detail in [13]. Based on the least squares method and the procedure for minimizing the mean-squared error of estimation, a discrete analog of the Wiener-Hopf equation is obtained, as well as Gaussian and Gaussian-Markov estimates (and estimates of their error covariance matrices) of the state vector of the observed system, which are linear unbiased and satisfy the minimum value of the mean-squared error of estimation [13]. The discrete Wiener-Hopf equation, Gaussian and Gaussian-Markov estimates with a minimum mean-squared error are used later to derive the discrete KF equations, that are a recurrent procedure in which at a discrete time
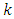 of the extrapolation (prediction) stage, based on the difference equations of the dynamics of the observed system, the estimate of the state vector is calculated for the next
of the extrapolation (prediction) stage, based on the difference equations of the dynamics of the observed system, the estimate of the state vector is calculated for the next 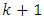 moment of time, and then, at the time
moment of time, and then, at the time 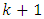 of the correction stage, based on new measurement of the system output signal and the changed value of the KF gain, the estimate of the state vector of the system calculated at the time
of the correction stage, based on new measurement of the system output signal and the changed value of the KF gain, the estimate of the state vector of the system calculated at the time 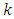 of extrapolation of the KF procedure is corrected [2-13].From the first application of the KF in the airspace the KF was a part of the Apollo onboard guidance [3] and to our days the KF has been demonstrating its usefulness in many various applications in different areas of technology and economics [14-16]. However, it is still not easy for people who are not familiar with the estimation theory to understand and implement the vector-matrix equations of the KF. Whereas there is a large number of excellent introductory materials and literature on the KF the purpose of this paper is to remind one simple method for deriving and explain the recursive algorithm for using the equations of the KF.
of extrapolation of the KF procedure is corrected [2-13].From the first application of the KF in the airspace the KF was a part of the Apollo onboard guidance [3] and to our days the KF has been demonstrating its usefulness in many various applications in different areas of technology and economics [14-16]. However, it is still not easy for people who are not familiar with the estimation theory to understand and implement the vector-matrix equations of the KF. Whereas there is a large number of excellent introductory materials and literature on the KF the purpose of this paper is to remind one simple method for deriving and explain the recursive algorithm for using the equations of the KF. 2. Notational Preliminaries
- All vectors and matrices are time-varying quantities are treated at the discrete time instants
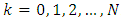 . By convention, the argument
. By convention, the argument 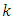 of vectors (e.g.,
of vectors (e.g., 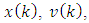 …) and matrices (e.g.,
…) and matrices (e.g., 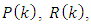 …) denotes the fact that the values of these variables correspond to the
…) denotes the fact that the values of these variables correspond to the 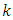 th step of time. The notation
th step of time. The notation 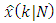 designates that the value of the estimation vector
designates that the value of the estimation vector 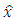 at the time instant
at the time instant 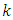 conditioned on
conditioned on 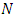 time instant measurements. If
time instant measurements. If  we are estimating a future value of
we are estimating a future value of 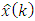 , and we refer to this as a predicted estimate. The case
, and we refer to this as a predicted estimate. The case 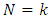 is referred to as a filtered estimate. Prediction and filtering make up the algorithm of KF and can be done in real time [6-8].The list of notations used through the paper is summarized in the Table 1.
is referred to as a filtered estimate. Prediction and filtering make up the algorithm of KF and can be done in real time [6-8].The list of notations used through the paper is summarized in the Table 1.
|
3. The Basic Model and the Problem of the State Estimation
- Consider the basic linear, time-varying (nonstationary), discrete-time state variable model of dynamical systems [5,6] as:
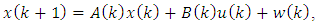 | (1) |
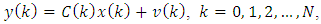 | (2) |
 is a
is a  state vector;
state vector; 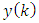 is a
is a 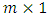 measurement vector;
measurement vector; 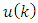 is
is 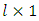 input vector;
input vector; 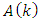 is
is 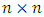 system matrix;
system matrix; 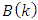 is
is 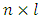 input matrix;
input matrix; 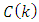 is
is 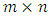 measurement matrix.
measurement matrix. 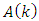 ,
, 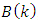 ,
, 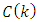 matrices and
matrices and 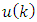 vector are known.Additionally,
vector are known.Additionally, 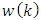 is
is 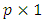 Gaussian white noise sequence of model uncertainties and disturbances and
Gaussian white noise sequence of model uncertainties and disturbances and 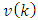 is
is 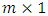 Gaussian white noise sequence of measurement inaccuracies, i.e.,
Gaussian white noise sequence of measurement inaccuracies, i.e.,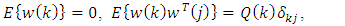 | (3) |
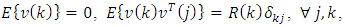 | (4) |
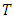 denotes the matrix transposition.
denotes the matrix transposition.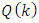 ,
, 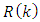 are
are 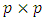 and
and  covariance matrices, respectively,
covariance matrices, respectively, 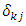 is the Dirac delta function, i.e.,
is the Dirac delta function, i.e., 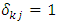 for
for 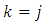 and
and 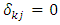 for
for 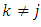 . Supposed that
. Supposed that 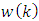 and
and 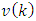 are mutually uncorrelated, i.e.,
are mutually uncorrelated, i.e.,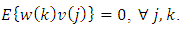 | (5) |
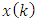 is zero mean and has a
is zero mean and has a 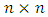 covariance matrix
covariance matrix 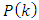 , i.e.,
, i.e.,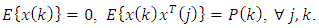 | (6) |
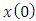 and its covariance matrix
and its covariance matrix 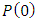 are known and
are known and 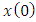 is uncorrelated with
is uncorrelated with 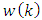 and
and 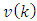 , i.e.,
, i.e.,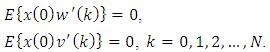 | (7) |
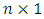 unknown state vector
unknown state vector 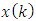 at
at 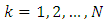 from the
from the 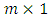 noisy measurement vector
noisy measurement vector 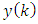 , where
, where 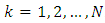 .The estimate
.The estimate 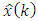 of a state vector
of a state vector 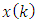 must be: 1) linear, 2) unbiased, i.e.,
must be: 1) linear, 2) unbiased, i.e., 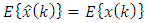 and must have 3) a minimum value of the mean of the squared error
and must have 3) a minimum value of the mean of the squared error 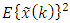 , i.e.,
, i.e.,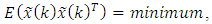 | (8) |
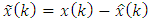 is the error in the estimate.Thus, there is the mean-squared estimation problem: given the noisy measurements
is the error in the estimate.Thus, there is the mean-squared estimation problem: given the noisy measurements 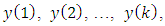 determine a linear unbiased estimator of the entire state vector
determine a linear unbiased estimator of the entire state vector 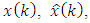 such that the conditional mean-squared error in the estimate
such that the conditional mean-squared error in the estimate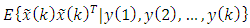 | (9) |
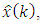 can also be called as the minimum variance estimator, since
can also be called as the minimum variance estimator, since 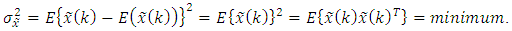 | (10) |
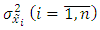 variances are diagonal elements of
variances are diagonal elements of 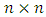 error-covariance matrix defined by [6]:
error-covariance matrix defined by [6]: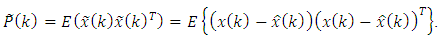 | (11) |
4. The Method of Minimizing of the Mean-Squared Error of Estimation
- To obtain the expressions for estimates
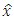 of unknown vector
of unknown vector 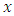 from the measurement vector
from the measurement vector 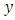 in conditions of measurement noises
in conditions of measurement noises 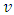 according to the Eq. (2) let’s consider the generic linear observation model [5]:
according to the Eq. (2) let’s consider the generic linear observation model [5]: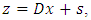 | (12) |
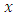 is an
is an 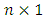 unknown vector,
unknown vector, 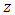 is a known
is a known 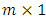 measurement vector,
measurement vector, 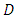 is a known
is a known 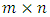 measurement matrix,
measurement matrix, 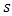 is an unknown
is an unknown 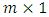 vector of measurement errors.The unknown quantities
vector of measurement errors.The unknown quantities 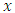 and
and 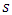 are random variables with the following expectations and covariance matrices and they are mutually uncorrelated, i.e.:
are random variables with the following expectations and covariance matrices and they are mutually uncorrelated, i.e.: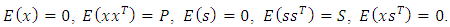 | (13) |
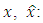
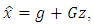 | (14) |
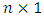 vector
vector 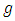 and
and 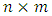 matrix
matrix 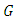 must determine, however, the request of the unbiased estimation means that:
must determine, however, the request of the unbiased estimation means that: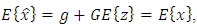 hence
hence 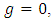 since
since 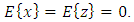 Thus the Eq. (14) for
Thus the Eq. (14) for  becomes as:
becomes as: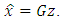 | (15) |
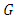 will be determined from the condition that the variance of estimation error
will be determined from the condition that the variance of estimation error 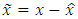 is minimum. According to Eq. (15) every component
is minimum. According to Eq. (15) every component 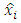 of
of 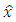 is depended on vector
is depended on vector 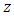 via an
via an 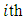 row of matrix
row of matrix 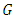 which is denoted as
which is denoted as 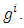 Thus
Thus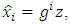 | (16) |
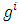 is the row vector.Mentioned request about a minimum variance of estimation error signifies that
is the row vector.Mentioned request about a minimum variance of estimation error signifies that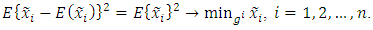 | (17) |
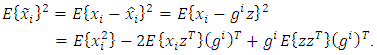 | (18) |
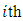 error is the sum in which the first term don’t depend on
error is the sum in which the first term don’t depend on 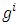 , the second and third terms are linear and quadratic forms of
, the second and third terms are linear and quadratic forms of 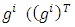 is the column vector). A necessary condition of minimum of Eq. (18) is that all its partial derivatives with respect to
is the column vector). A necessary condition of minimum of Eq. (18) is that all its partial derivatives with respect to 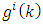 must be equal to zero. In other words, taking the gradient of
must be equal to zero. In other words, taking the gradient of 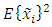 with respect to
with respect to 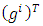 must be equal to zero, i.e.,
must be equal to zero, i.e.,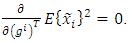 | (19) |
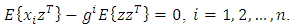 | (20) |
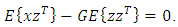 | (21) |
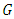 is that the variance
is that the variance 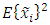 of each
of each 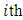 estimation error must be extremum. The sufficient condition of it is the positive definiteness of the matrix formed by the second derivatives of the function
estimation error must be extremum. The sufficient condition of it is the positive definiteness of the matrix formed by the second derivatives of the function 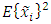 with respect to
with respect to 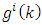 . In other words, the Hessian matrix with respect to
. In other words, the Hessian matrix with respect to 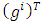 must be positive definite for all
must be positive definite for all 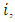 i.e.:
i.e.: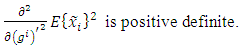 | (22) |
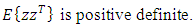 | (23) |
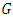 .To obtain the matrix
.To obtain the matrix 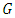 we must find the covariance matrices in Eq. (21), so taking into account the Eqs. (12), (13) we have:
we must find the covariance matrices in Eq. (21), so taking into account the Eqs. (12), (13) we have: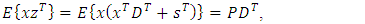 | (24) |
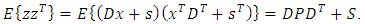 | (25) |
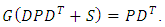 | (26) |
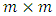 matrix. If
matrix. If 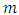 measurements are less than
measurements are less than 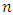 unknowns, then from the Eq. (26) we can find the matrix
unknowns, then from the Eq. (26) we can find the matrix 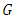 :
: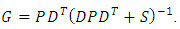 | (27) |
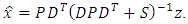 | (28) |
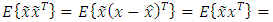 | (29) |
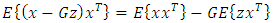 | (30) |
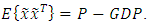 | (31) |
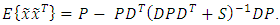 | (32) |
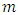 measurements are more than
measurements are more than 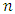 unknowns, the Eq. (26) can be transformed to the following form [13]:
unknowns, the Eq. (26) can be transformed to the following form [13]: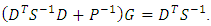 | (33) |
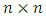 matrix. Using matrix
matrix. Using matrix 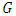 obtained from the Eq. (33) the second form of the linear unbiased estimate with a minimum value of mean-squared estimation error is:
obtained from the Eq. (33) the second form of the linear unbiased estimate with a minimum value of mean-squared estimation error is: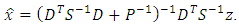 | (34) |
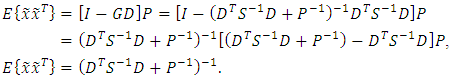 | (35) |
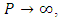 that is
that is 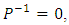 and rank of matrix
and rank of matrix 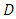 is
is 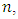 then we have the Gaussian-Markov estimate [13]:
then we have the Gaussian-Markov estimate [13]: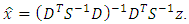 | (36) |
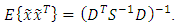 | (37) |
5. Deriving the Equations of the Kalman Filter
- The Kalman filter operates in a predict-correct manner [5].
5.1. Prediction
- At the initial observation moment according to the Eqs. (2), (6) the following measuring is obtained:
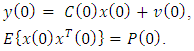 | (38) |
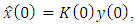 | (39) |
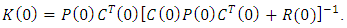 | (40) |
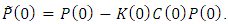 | (41) |
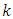 to
to 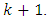 With this aim consider the discrete Wiener-Hopf equation (21) which is the necessary and sufficient condition that estimate will have a minimum mean-squared error. Rewrite Eq. (21) in more short form:
With this aim consider the discrete Wiener-Hopf equation (21) which is the necessary and sufficient condition that estimate will have a minimum mean-squared error. Rewrite Eq. (21) in more short form: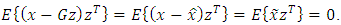 | (42) |
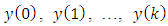 are already done and the estimate
are already done and the estimate 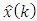 with the minimum of the mean-squared error is obtained. The latter means that the Eq. (42) is satisfied, i.e.:
with the minimum of the mean-squared error is obtained. The latter means that the Eq. (42) is satisfied, i.e.: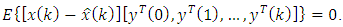 | (43) |
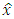 and
and 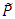 at the time
at the time 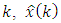 and
and 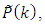 are known. According to the Eq. (1) let’s find the predicted value of
are known. According to the Eq. (1) let’s find the predicted value of 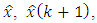 herewith uncertainties and disturbances
herewith uncertainties and disturbances 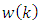 (with zero expectations) are not taken into account:
(with zero expectations) are not taken into account: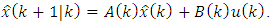 | (I) |
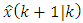 is optimal. According to Eq. (42) we have:
is optimal. According to Eq. (42) we have: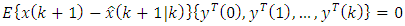 | (44) |
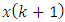 with
with 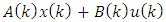 from the Eq. (1), herewith disturbances
from the Eq. (1), herewith disturbances 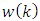 cannot be taken into account because they are not correlated with
cannot be taken into account because they are not correlated with 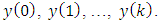 We have the following equation:
We have the following equation: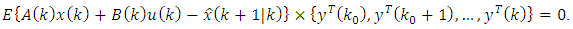 | (45) |
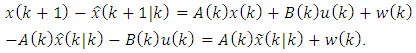 | (46) |
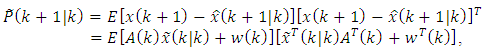 however, the noises
however, the noises 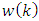 are not correlated with the estimation errors
are not correlated with the estimation errors 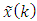 , so
, so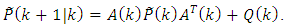 | (II) |
5.2. Correction
- The estimate of the predicted state vector
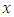 at the
at the 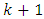 instant of time,
instant of time, 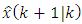 , obtained with the available
, obtained with the available 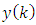 measurement (Eq. (I)), after the next
measurement (Eq. (I)), after the next 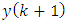 measurement must be corrected to the value
measurement must be corrected to the value 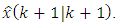 In order to find
In order to find 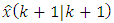 let’s replace
let’s replace 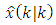 in Eq. (I) with
in Eq. (I) with 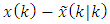 and substitute instead of
and substitute instead of 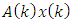 the corresponding expression from the Eq. (1):
the corresponding expression from the Eq. (1):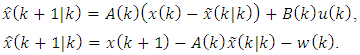 | (47) |
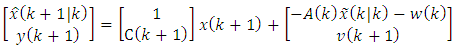 | (48) |
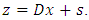 | (49) |
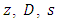 are defined through comparing the Eqs. (48), (49). The covariance matrix of the upper part of vector
are defined through comparing the Eqs. (48), (49). The covariance matrix of the upper part of vector 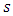 was earlier denoted as
was earlier denoted as 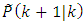 , the covariance matrix of the lower part
, the covariance matrix of the lower part 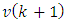 is equal to
is equal to 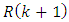 . Covariance between
. Covariance between 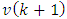 and
and 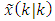 and between
and between 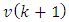 and
and 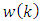 are equal to zero. So, we have:
are equal to zero. So, we have: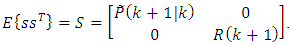 | (50) |
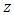 contains the component
contains the component 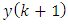 we can calculate Gaussian-Markov estimate
we can calculate Gaussian-Markov estimate 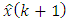 at the
at the 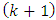 instant of time according to the Eqs. (36), (37), i.e.:
instant of time according to the Eqs. (36), (37), i.e.: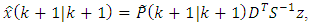 | (51) |
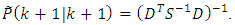 | (52) |
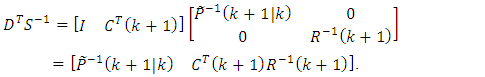 | (53) |
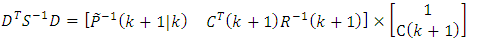 | (54) |
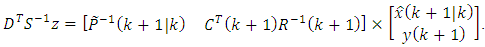 | (55) |
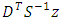 from the Eq. (55) into the Eq. (51) of Gaussian-Markov estimate:
from the Eq. (55) into the Eq. (51) of Gaussian-Markov estimate: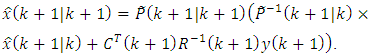 | (56) |
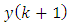 is the gain matrix
is the gain matrix 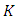 :
: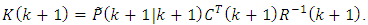 | (57) |
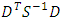 and taking into account the Eq. (52) we receive:
and taking into account the Eq. (52) we receive: 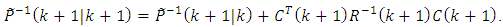 | (58) |
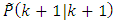 on the left the Eq. (58) and taking into account the Eq. (57) we receive:
on the left the Eq. (58) and taking into account the Eq. (57) we receive: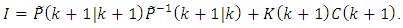 | (59) |
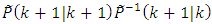 from the Eq. (59) and substitute it into the Eq. (56):
from the Eq. (59) and substitute it into the Eq. (56):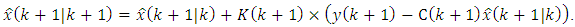 | (III) |
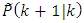 on the right the Eq. (59):
on the right the Eq. (59):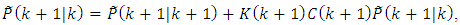 and from this equation we can receive the error-covariance matrix:
and from this equation we can receive the error-covariance matrix: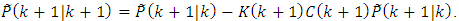 | (IV) |
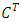 on the right and ascribe to the first tirm in the right hand side the factor
on the right and ascribe to the first tirm in the right hand side the factor 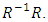 From the obtained equation taking into account the Eq. (57) we can find the gain matrix
From the obtained equation taking into account the Eq. (57) we can find the gain matrix 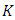 :
: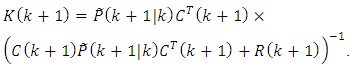 | (V) |
6. The Theorem of the Kalman Filter
- The Eqs. (39)-(41) and (I)-(V) make up together the Kalman filter which is usually formulated as the theorem. Let’s present the formulation of the theorem of Kalman filter satisfying the minimum of mean-squared error of estimation.Theorem (The Kalman Filter). Let given a discrete stochastic system defined by the Eqs. (1)-(7) and considered at
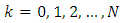 instants of time. The linear unbiased estimate with the minimum mean-squared error in the estimation of the state vector of this system at any time instant
instants of time. The linear unbiased estimate with the minimum mean-squared error in the estimation of the state vector of this system at any time instant 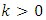 is obtained by the recursive equations (I)-(V) the initial state of which at
is obtained by the recursive equations (I)-(V) the initial state of which at 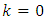 is determined by the equations (39)-(41).In addition to the proof of the theorem considered above to check the correctness of the Eqs. (IV), (V). With this aim let’s make the expression for
is determined by the equations (39)-(41).In addition to the proof of the theorem considered above to check the correctness of the Eqs. (IV), (V). With this aim let’s make the expression for 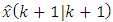 according to the Eq. (42):
according to the Eq. (42):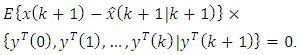 | (60) |
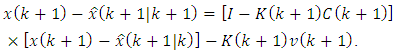 | (61) |
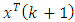 and calculate expectation. Still, using the Eq. (42) will allow us to obtain the Eq. (IV).To check the correctness of the deriving the Eq. (V), consider the first part of the mathematical expectation in Eq. (60), containing values from
and calculate expectation. Still, using the Eq. (42) will allow us to obtain the Eq. (IV).To check the correctness of the deriving the Eq. (V), consider the first part of the mathematical expectation in Eq. (60), containing values from 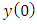 to
to 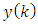 and located to the left of the vertical line for
and located to the left of the vertical line for 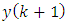 . The new measurement error
. The new measurement error 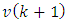 is uncorrelated with the old observations from
is uncorrelated with the old observations from 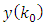 to
to 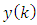 . The product of two expressions in square brackets in (61), correlated with the set of observations from
. The product of two expressions in square brackets in (61), correlated with the set of observations from 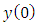 to
to 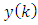 , means zero mathematical expectation according to equation (44). This means that expression (III) satisfies the part of the requirement (42) that is to the left of the vertical line. The remaining part of the requirement (60) allows us to determine the undefined gain matrix
, means zero mathematical expectation according to equation (44). This means that expression (III) satisfies the part of the requirement (42) that is to the left of the vertical line. The remaining part of the requirement (60) allows us to determine the undefined gain matrix 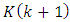 . On the basis of (61), the following equality must be valid:
. On the basis of (61), the following equality must be valid: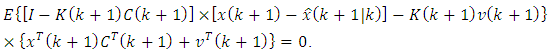 | (62) |
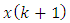 and
and 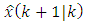 are not correlated with
are not correlated with 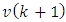 . The rest of the mathematical expectations can be represented in a simpler form. To do this, we use Eq. (29) with respect to
. The rest of the mathematical expectations can be represented in a simpler form. To do this, we use Eq. (29) with respect to 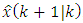 , taking into account that the covariance between
, taking into account that the covariance between 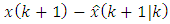 and
and 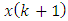 can be replaced by
can be replaced by 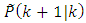 . As a result, we have:
. As a result, we have: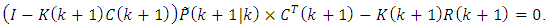 | (63) |
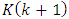 we’ll receive the Eq. (V).
we’ll receive the Eq. (V).7. The Algorithm of Using the Equations of the Kalman Filter
- The Kalman filter is a recursive procedure that is convenient for program realization on computers. The algorithm of using the Eqs. (39)-(41) and (I)-(V) of KF is the following as:1) At the initial state
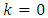 the initial estimate of the state vector
the initial estimate of the state vector 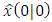 and the initial error-covariance matrix
and the initial error-covariance matrix 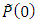 are built according to the Eqs. (39)-(41):
are built according to the Eqs. (39)-(41):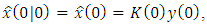 where
where 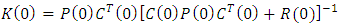 and
and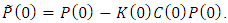 2) The estimate and its error-covariance matrix are extrapolated to the next
2) The estimate and its error-covariance matrix are extrapolated to the next 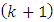 observation instant of time according to the Eqs. (I), (II):
observation instant of time according to the Eqs. (I), (II):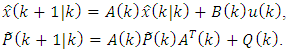 Correction:3) The optimal gain matrix
Correction:3) The optimal gain matrix 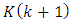 is calculated according to the Eq. (V) and extrapolated (predicted) estimate
is calculated according to the Eq. (V) and extrapolated (predicted) estimate 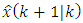 is improved to the value
is improved to the value 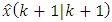 according to the Eq. (III) using the new measurement
according to the Eq. (III) using the new measurement 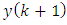 :
: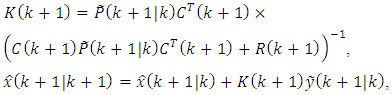 where
where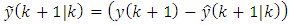 is called the innovation process,
is called the innovation process,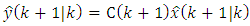 is called the predicted value of the new measurement.4) The error-covariance matrix
is called the predicted value of the new measurement.4) The error-covariance matrix 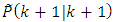 of the new modified estimate
of the new modified estimate 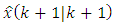 is calculated according to the Eq. (IV):
is calculated according to the Eq. (IV):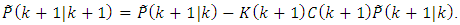 5) If the next
5) If the next 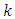 is
is 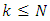 then the current time instant
then the current time instant 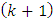 should be considered as
should be considered as 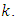 For the estimate of the state calculated at the step 3 and now considered as
For the estimate of the state calculated at the step 3 and now considered as 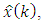 for the error-covariance matrix calculated at the step 4 and now considered as
for the error-covariance matrix calculated at the step 4 and now considered as 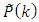 should be carried out the steps 2, 3 and 4 of the algorithm. If
should be carried out the steps 2, 3 and 4 of the algorithm. If 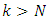 then the procedure is ended.Therefore, the best estimate of
then the procedure is ended.Therefore, the best estimate of 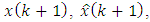 using all observations up to and including
using all observations up to and including 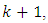 is obtained by a predictor step,
is obtained by a predictor step, 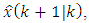 and a corrector step,
and a corrector step, 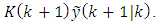 The predictor step uses information from the state equation (1). The corrector step uses the new measurement available at
The predictor step uses information from the state equation (1). The corrector step uses the new measurement available at 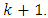 The correction is the error (difference) between new measurement,
The correction is the error (difference) between new measurement, 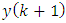 , and its best predicted value,
, and its best predicted value, 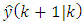 , multiplied by weighting (or gain) factor
, multiplied by weighting (or gain) factor 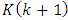 . The factor
. The factor 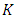 determines how much we will alter (change) the best estimate
determines how much we will alter (change) the best estimate 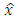 based on the new observation, i.e., 1) if the elements of
based on the new observation, i.e., 1) if the elements of 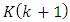 are small, we have considerable confidence in our model, and 2) if they are large, we have considerable confidence in our observation measurements. Thus, the KF is a dynamical feedback system, its gain matrix and predicted- and filtering-error covariance matrices comprise a matrix feedback system operating within the KF [5,6].
are small, we have considerable confidence in our model, and 2) if they are large, we have considerable confidence in our observation measurements. Thus, the KF is a dynamical feedback system, its gain matrix and predicted- and filtering-error covariance matrices comprise a matrix feedback system operating within the KF [5,6].8. Conclusions
- The discrete Kalman filter, developed by R. Kalman back in 1960 [19], is currently a classic result of the theory of control systems and the theory of signal processing, as well as the most popular filtering algorithm using in automatic control systems, telecommunications and information systems subjected to random disturbances and measurement inaccuracies. The Kalman filter is a recursive procedure consisting of difference vector-matrix equations for calculating estimates of the state of a stochastic system, the estimates of the error covariance matrices and the filter gain. A common approach to the derivation of the KF equations is the Bayesian approach [11]. The paper describes the simplest way to obtain the KF equations, based on the use of the procedure for minimizing the mean-squared error of estimation, which is a further generalization of the least squares method [12]. As a result of this procedure, we obtained: a discrete analog of the Wiener-Hopf equation, as well as Gaussian and Gaussian-Markov estimates (and their error covariance matrices), which are linear and unbiased and satisfy the minimum value of the mean-squared error of the estimation. Based on the discrete Wiener-Hopf equation, Gaussian and Gaussian-Markov estimates, the KF equations are obtained using simple algebraic transformations and reasoning. The KF theorem is formulated, which satisfies the minimum of mean-squared error of estimation, and the algorithm for using the KF equations, which is convenient for program realization, is also explained.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML