-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2020; 10(1): 11-15
doi:10.5923/j.control.20201001.02

Stability and Feedback Control of Nonlinear Systems
Abraham C. Lucky, Davies Iyai, Cotterell T. Stanley, Amadi E. Humphrey
Department of Mathematics, Rivers State University, Port Harcourt, Rivers State, Nigeria
Correspondence to: Davies Iyai, Department of Mathematics, Rivers State University, Port Harcourt, Rivers State, Nigeria.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, new results for stability and feedback control of nonlinear systems are proposed. The results are obtained by using the Lyapunov indirect method to approximate the behavior of the uncontrolled nonlinear system’s trajectory near the critical point using Jacobian method and designing state feedback controller for the stabilization of the controlled nonlinear system using the difference in response between the set point and actual output values of the system. Next, the Lyapunov-Razumikhin method is used to determine sufficient conditions for the stabilization of the system. Examples are given with simulation output studies to verify the theoretical analysis and numerical computations using MATLAB.
Keywords: Stability, Lyapunov method, Feedback control, Mass spring damper, Nonlinear system
Cite this paper: Abraham C. Lucky, Davies Iyai, Cotterell T. Stanley, Amadi E. Humphrey, Stability and Feedback Control of Nonlinear Systems, International Journal of Control Science and Engineering, Vol. 10 No. 1, 2020, pp. 11-15. doi: 10.5923/j.control.20201001.02.
Article Outline
1. Introduction
- Stability and control of nonlinear systems with control inputs is in no doubt one of the popular research interest in modern systems and control theory when compared to linear systems and has attracted lots of research [1,2,3,4] because of its wide range of applications. There are several studies on the stability [5,6,7] and controllability [8,9] of nonlinear control systems aimed at providing desired response to a design goal. The stability analysis and control synthesis of nonlinear control systems play significant role in many real life control problems which includes stabilizing, tracking, and disturbance rejection or attenuation of systems. A nonlinear control system is considered as a system in which the static characteristics between input and output have a nonlinear relationship. A significant interconnection used for nonlinear control systems is the feedback configuration. The effect of feedback on system response depends on the design goals and several formulations of such nonlinear control problems and method of approach exists in classical control theory see for example [10,11,12] and [13]. A feedback system could be a negative or positive and is often referred to as a closed-loop system. In a feedback system, a fraction of the output values is ‘fed back’ and either added to (positive feedback) or subtracted from (negative feedback) the original set reference point. That is; the output continually updates its input in order to modify the system responses and improve stability. Several methods are used to analyze or improve the stability and stabilization of nonlinear control system which as seen in [14,15] and references therein includes fixed point based, spectral radius and the Lyapunov based. The stability and stabilization of nonlinear control systems has been studied by many including [7,16] and [17]. For example, in [16], the stabilization of second-order systems by non-linear position feedback was investigated by placing actuators and sensors in the same location; and using a parallel compensator to obtain asymptotic stability results for the closed-loop system by LaSalle’s theorem. In [17], the stabilization of second order system with a time delay controller was analyzed using Padẽ approximation to obtain stability regions by constrained optimization; these regions are then used to optimize the impulse response of the closed loop systems and approximated the performance index with James-Nichols-Philips theorem. The spectral conditions for stability and stabilization of nonlinear co-operative systems associated to vector fields that are concave was studied in [18], using spectral radius of the Jacobian for the system where they provided conditions that guaranteed existence, uniqueness and stability of strictly positive equilibria. The fixed point and stability of nonlinear equations with variable delays was investigated in [19], were they obtained conditions for the boundedness and stability of the system using contraction mapping principle.In [7], new stability and controllability results for nonlinear systems were established in their study of the stability and controllability of nonlinear systems using the Lyapunov and Jacobi’s linearization methods to obtain their stability results; and the rank criterion for properness for their controllability results. The focus on this paper is the Lyapunov based approach which includes the direct and indirect method of Lyapunov. Even though the Lyapunov direct method is an effective way of investigating nonlinear systems and obtaining global results on stability of systems. This research follows similar standpoint with that of [7] by using the Lyapunov indirect method, where instead of looking for a Lyapunov function to be applied directly to the nonlinear system; the idea of linearization around a given point is used to achieve stability on some region [20] using quadratic Lyapunov functions but extends their results by designing state feedback controller for the stabilization of such systems. Next, we use the Lyapunov-Razumikhin method to explore the possibility of using the rate of change of a function on
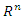 to determine sufficient condition for the stabilization of the feedback system. The rest of the paper is organized in the following order; Section 2 contains preliminaries and definitions on the subject areas as guide to the research methodology. Section 3 contains stability results on the equilibrium point for the system while Section 4 contains the main results of this research; with application and simulation output result illustrating the effectiveness of the study given in Section 5 prior to the conclusion in Section 6.
to determine sufficient condition for the stabilization of the feedback system. The rest of the paper is organized in the following order; Section 2 contains preliminaries and definitions on the subject areas as guide to the research methodology. Section 3 contains stability results on the equilibrium point for the system while Section 4 contains the main results of this research; with application and simulation output result illustrating the effectiveness of the study given in Section 5 prior to the conclusion in Section 6. 2. Preliminaries and Definitions
- Let
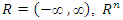 is a real
is a real 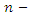 dimensional Euclidean space with norm
dimensional Euclidean space with norm 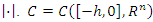 is the space of continuous function mapping the interval
is the space of continuous function mapping the interval  into
into  with the norm
with the norm  where
where 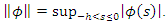 Define the symbol
Define the symbol 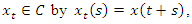
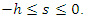 Here, we consider only initial data satisfying the condition
Here, we consider only initial data satisfying the condition 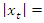
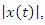 that is,
that is, 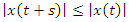 for all
for all 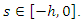
2.1. Preliminaries
- We consider the autonomous system
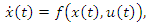 | (1) |
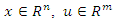 and
and 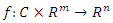 is a continuously differentiable function and define
is a continuously differentiable function and define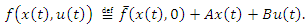 | (2) |
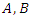 are
are  and
and 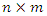 constant matrices respectively,
constant matrices respectively, 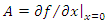 ,
, 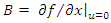 and
and 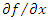 denotes the Jaciobian matrix.
denotes the Jaciobian matrix. 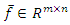 satisfies the condition
satisfies the condition 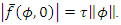 Consider system (1) with all its necessary assumptions given by
Consider system (1) with all its necessary assumptions given by 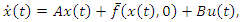 | (3) |
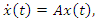 | (4) |
2.2. Definitions
- We now give some definitions that underpins the subject areas of this research work.Definition 2.1. The equilibrium point
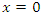 of system (3) is stable if for any
of system (3) is stable if for any 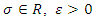 there exists a
there exists a 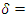
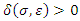 such that if
such that if 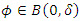 implies
implies 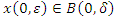 for
for 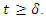 Definition 2.2. The equilibrium point
Definition 2.2. The equilibrium point 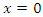 of system (3) is asymptotically stable if it is stable and there is
of system (3) is asymptotically stable if it is stable and there is 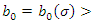
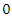 such that
such that 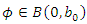 implies
implies 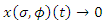 as
as 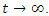 Definition 2.3. The solution
Definition 2.3. The solution 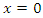 of system (3) is uniformly stable if
of system (3) is uniformly stable if 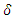 Definition 1 is independent of
Definition 1 is independent of 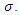 Definition 2.4. The solution
Definition 2.4. The solution 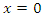 of system (3) is uniformly asymptotically stable, if it is uniformly stable and there exist
of system (3) is uniformly asymptotically stable, if it is uniformly stable and there exist 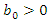 such that every
such that every 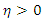 there is a
there is a 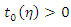 such that
such that 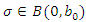 implies
implies 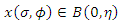 for
for 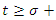
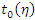 .
.3. Stability Result
- Consider system (1) with
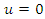 given by
given by 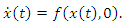 | (5) |
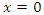 is an equilibrium point for the system (5) with
is an equilibrium point for the system (5) with 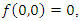 for all
for all 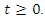 Let
Let 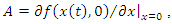 | (6) |
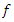 with respect to
with respect to 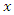 at the origin such that
at the origin such that 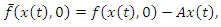 | (7) |
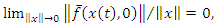 | (8) |
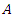 be defined by equation (6), so that it can be approximated by (4).Then, the origin is a. Asymptotically stable if the origin of the linearized system (5) is asymptotically stable, i.e. if the matrix A is Hurwitz namely the eigenvalues of A lies on
be defined by equation (6), so that it can be approximated by (4).Then, the origin is a. Asymptotically stable if the origin of the linearized system (5) is asymptotically stable, i.e. if the matrix A is Hurwitz namely the eigenvalues of A lies on 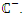 b. Unstable if the origin of the linearized system (5) is unstable i.e. if one or more eigenvalues of A lie in
b. Unstable if the origin of the linearized system (5) is unstable i.e. if one or more eigenvalues of A lie in 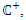 the open right-half of the complex plane. Proof: The proof is given in [7] and therefore omitted.
the open right-half of the complex plane. Proof: The proof is given in [7] and therefore omitted.4. Feedback Control of System
- The main results of this paper will be stated as theorems in this section. The proofs of the next two theorems follow along the lines of the proofs of Theorem 4.1and 4.2 in [21].Theorem 4.1. Suppose there are continuous non-decreasing, nonnegative functions
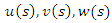 with
with 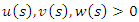 for
for 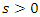 and
and 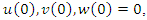 and there is a continuous function
and there is a continuous function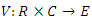 such that(i)
such that(i) 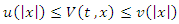 (ii)
(ii) 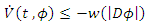 , for all
, for all 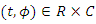 satisfying
satisfying 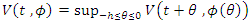 . Then the zero solution of system (3) is uniformly stable. Theorem 4.2. Let
. Then the zero solution of system (3) is uniformly stable. Theorem 4.2. Let 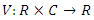 be the function satisfying condition (i) in Theorem 4.1, and if in addition there exists constant
be the function satisfying condition (i) in Theorem 4.1, and if in addition there exists constant 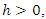 a continuous non-decreasing, nonnegative functions
a continuous non-decreasing, nonnegative functions 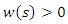 for
for 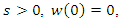 and a continuous function
and a continuous function 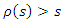 for
for 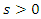 such that condition (ii) in Theorem 4.1 is strengthened to(iii)
such that condition (ii) in Theorem 4.1 is strengthened to(iii) 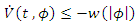 for all
for all 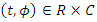 satisfying
satisfying 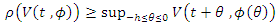 . Then the zero solution of (3) is uniformly asymptotically stable.
. Then the zero solution of (3) is uniformly asymptotically stable.4.1. Main Results
- Theorem 4.3. Consider system (1), with all its assumptions. If
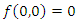 and the linearized system
and the linearized system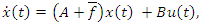 | (9) |
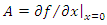 and
and 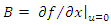 is such that
is such that 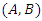 is a controllable pair. Then, there exists a matrix
is a controllable pair. Then, there exists a matrix 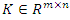 such that all the eigen-values of
such that all the eigen-values of 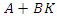 are in
are in 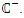 Furthermore, using the control law
Furthermore, using the control law 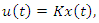 the equilibrium
the equilibrium 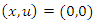 is asymptotically stable for the closed loop system. Proof. Assume that
is asymptotically stable for the closed loop system. Proof. Assume that 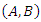 is controllable, then by the Hautus criterion for controllability
is controllable, then by the Hautus criterion for controllability 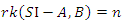 for some
for some 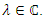 We proof by contraposition. Assume that
We proof by contraposition. Assume that 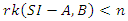 for some
for some 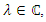 then by the Kalman controllability decomposition lemma; there exists
then by the Kalman controllability decomposition lemma; there exists 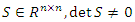 such that:
such that: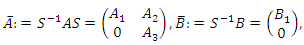 where the pair
where the pair 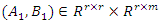 is controllable with
is controllable with 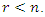 Now, the equilibrium of the linearized system (9) will be asymptotically stable if there exist
Now, the equilibrium of the linearized system (9) will be asymptotically stable if there exist 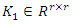 such that
such that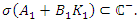 | (10) |
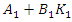 have negative real parts. Defining
have negative real parts. Defining 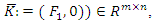 we have
we have 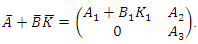 Let
Let 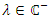 and
and 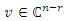 be eigenvalue/eigenvector pair of
be eigenvalue/eigenvector pair of 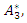 so that
so that 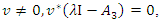 setting
setting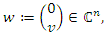 it follows that
it follows that 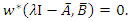 Consequently,
Consequently, 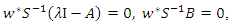 showing that
showing that 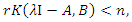 and
and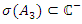 | (11) |
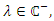 by the stability criteria and therefore
by the stability criteria and therefore 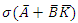 | (12) |
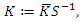 we get
we get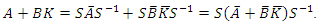 Therefore,
Therefore, 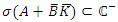 by (4.4) and the theorem is proved.We now use the Razumikhin method to find the uniform asymptotic stability of the system. It is known from theorem of Lyapunov matrix equation that, there is a symmetric positive definite matrix
by (4.4) and the theorem is proved.We now use the Razumikhin method to find the uniform asymptotic stability of the system. It is known from theorem of Lyapunov matrix equation that, there is a symmetric positive definite matrix 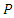 such that
such that 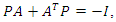 where I is the identity matrix and
where I is the identity matrix and 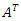 is the transpose of
is the transpose of 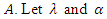 be positive numbers such that
be positive numbers such that 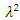 and
and 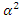 are the least and greatest Eigen-values of
are the least and greatest Eigen-values of 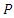 respectively. Then, it is clear that,
respectively. Then, it is clear that, 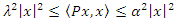 , for all
, for all 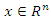 . Making use of the assumptions on the equation (3) we now develop a new theorem for uniform asymptotic stability.Theorem 4.4. Let all the assumptions on system (3) be satisfied, such that
. Making use of the assumptions on the equation (3) we now develop a new theorem for uniform asymptotic stability.Theorem 4.4. Let all the assumptions on system (3) be satisfied, such that 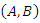 is a controllable pair and suppose,
is a controllable pair and suppose, 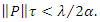 | (13) |
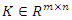 such that using the control law
such that using the control law 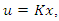 the equilibrium
the equilibrium 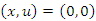 of the closed loop system
of the closed loop system 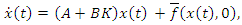 | (14) |
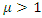 so that
so that 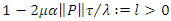 . Now, let
. Now, let 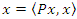 . It is necessary to prove that
. It is necessary to prove that 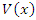 satisfies all the conditions in Theorem 4.2 for system (14). It is obvious that conditions (i) of Theorem 4.1 holds, assume now that
satisfies all the conditions in Theorem 4.2 for system (14). It is obvious that conditions (i) of Theorem 4.1 holds, assume now that 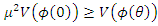 , so that
, so that 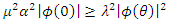 and hence
and hence 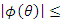
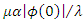 for all
for all 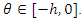 Then, the derivative
Then, the derivative 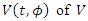 along the solution of equation (14) is given by
along the solution of equation (14) is given by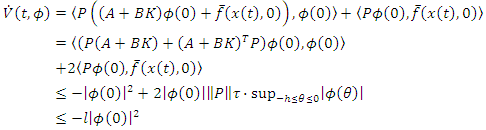 Thus, the condition of Theorem 4.2 holds if
Thus, the condition of Theorem 4.2 holds if 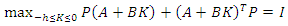 and there is a
and there is a 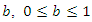 such that
such that 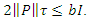 If in addition
If in addition 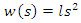 and
and 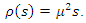 Then, the zero solution of system (14) is uniformly asymptotically stable.
Then, the zero solution of system (14) is uniformly asymptotically stable.5. Illustrative Examples
- Consider the modeling of a mass spring damper with mass
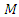 attached to a damper
attached to a damper 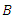 and a nonlinear spring
and a nonlinear spring 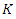 in [7] with all its necessary assumption given by
in [7] with all its necessary assumption given by 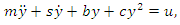 | (15) |
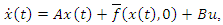 where
where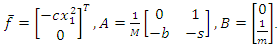 Example 5.1If the nonlinear system (15) is estimated by
Example 5.1If the nonlinear system (15) is estimated by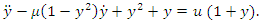 | (16) |
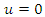 using Theorem 3.1 when evaluated gives two points of equilibrium
using Theorem 3.1 when evaluated gives two points of equilibrium 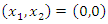 and
and 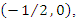 and Jacobian matrix is obtained as
and Jacobian matrix is obtained as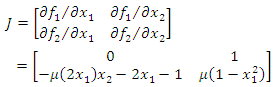 Evaluating the Jacobian at these two points gives
Evaluating the Jacobian at these two points gives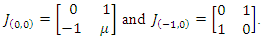 The linearized system matrix at equilibrium is a stable point for
The linearized system matrix at equilibrium is a stable point for 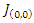 for all
for all 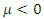 and unstable point for
and unstable point for 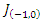 with
with 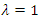 and
and 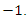 Since
Since 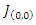 is stable point for all
is stable point for all 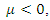 the first assumption of Theorem 3.1 is satisfied i.e.
the first assumption of Theorem 3.1 is satisfied i.e. 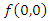 is an equilibrium point for all
is an equilibrium point for all 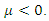 Next, we show that condition (8) of Theorem 3.1 is satisfied as follows. Let
Next, we show that condition (8) of Theorem 3.1 is satisfied as follows. Let 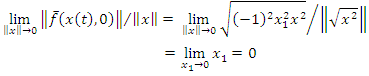 Thus, condition (8) is satisfied, hence system (16) is asymptotically stable. We now use the control law
Thus, condition (8) is satisfied, hence system (16) is asymptotically stable. We now use the control law 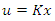 to stabilize the system, where
to stabilize the system, where 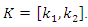 Observe by Theorem 4.3 that,
Observe by Theorem 4.3 that,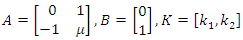 so that,
so that,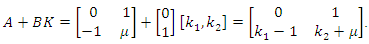 Hence,
Hence, 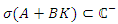 for
for 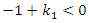 and
and 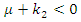 That is
That is 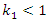 and
and 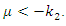 For simulation purposes with the feedback control law, we let
For simulation purposes with the feedback control law, we let 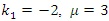 and
and 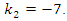 The simulation output with the feedback control law is given in Figure 1.
The simulation output with the feedback control law is given in Figure 1.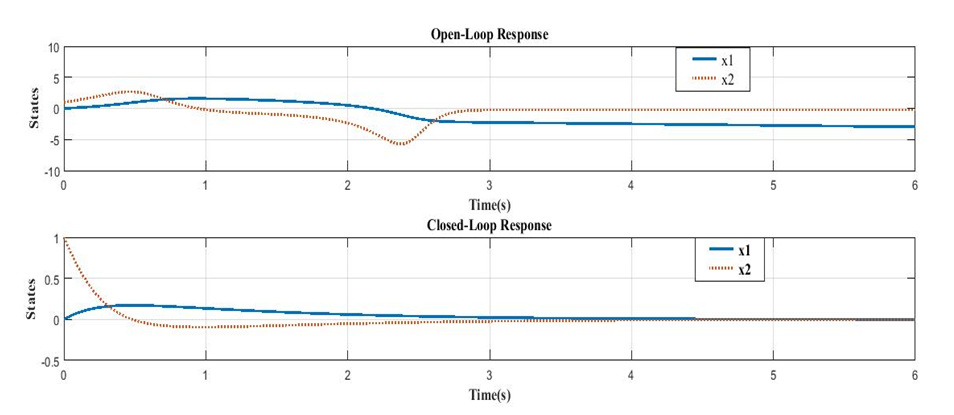 | Figure 1. Open and closed-loop responses of the system |
 and
and  be defined as in Example 5.1 with
be defined as in Example 5.1 with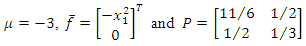 be the symmetric positive definite matrix with
be the symmetric positive definite matrix with 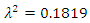 and
and 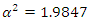 as the least and greatest eigenvalues respectively. Using the control law
as the least and greatest eigenvalues respectively. Using the control law 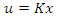 system (16) can be written in the form of equation (14) to be of the form
system (16) can be written in the form of equation (14) to be of the form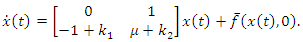 | (17) |
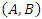 is controllable and the function
is controllable and the function 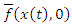 satisfies the condition
satisfies the condition 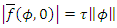 with
with 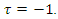 Check also that,
Check also that, 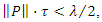 which satisfies the condition of Theorem 4.4. Moreover,
which satisfies the condition of Theorem 4.4. Moreover,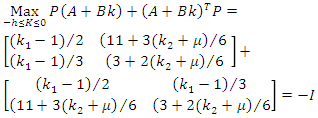 and
and 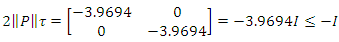 Therefore, the zero solution of system (14) is uniformly asymptotically stable.
Therefore, the zero solution of system (14) is uniformly asymptotically stable.6. Conclusions
- In this paper, the stability and feedback control results of nonlinear systems are presented with examples given. The Lyapunov indirect method and the Jacobian linearization methods were used to analyze stability and the stabilization of the system using feedback control law. Furthermore, the Lyapunov-Razumikhin method was used to determine sufficient conditions for the stabilization of the system using rate of change of a function on
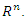 Examples are given to demonstrate the effectiveness of the theoretical results with simulation output studies using MATLAB also given as Figure 1. The simulation outputs shows the open and closed-loop responses of the system (16) where the states of the system for the open-loop oscillates without convergence while the states of the closed-loop system converges as regulated by the feedback control law.
Examples are given to demonstrate the effectiveness of the theoretical results with simulation output studies using MATLAB also given as Figure 1. The simulation outputs shows the open and closed-loop responses of the system (16) where the states of the system for the open-loop oscillates without convergence while the states of the closed-loop system converges as regulated by the feedback control law. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML