1. Introduction

The integration of real-time optimization (RTO) and control systems for an optimal plant operation is still an open research problem and attempts have been made to address the integration task in a systematic way. Use of RTO is the process of finding the set of conditions required to obtain the best economic result for a given condition; a method of determining a set of operating targets for the online control system to achieve the maximum profit possible within constraints and practical limits of the process equipment while keeping all the products at specifications [1,2,3]. RTO systems are advanced techniques or algorithms which evaluate process conditions and find an optimum solution to enhance the performance of the plant.

The real-time optimization strategies [1,2,3,4,5] have been designated in the literature by real-time optimization [6] or online optimization [7,8,9,10]. The model-based technique, is the most common RTO strategy available in commercial RTO systems [11,12,13] are widely used in the petroleum refineries [14,15,16,17], but may also be found in other sectors of the industry [18].

The RTO provides superior performance due to the use of process and kinetic models which are integrated into RTO framework [19,20]. This integration of accurate process models provides a platform to perform the real-time otimization and improves the overall performance of the plant to maximize the yield of high value products. [21,22].

The factor of plant-model mismatch is also important in real-time optimization applications as the more accurate are the process and kinetic models, the better will be the performnce of RTO [23,24,25,26]. This will also require modelling techniques to take into account the process constraints which will guarantee the optimality of process operation [27,28,29,30].

The other advantage of RTO is that it integrates process measurements into the optimization framework; ensuring process optimization does not rely exclusively on an inaccurate process model but also on process information stemming from measurements. In literature, various RTO techniques are available [31] and can be categorized into two broad families depending if the process model is used (explicit optimization) or not used (implicit optimization).

The present work aims at presenting the implementation techniques and performance evaluation of RTO systems on a hydrocracking unit on a model case refinery in the Middle East. The aim is to highlight some features of RTO systems, which have brought higher benefits to the refinery by maximizing the economic objective functions. In addition, potential RTO applications have been highlighted for achieving CO₂ emission reduction using two different approaches: improvement of energy efficiency and application of CO₂ capture and conversion technologies. This application will integrate MPC with real-time optimization with an ultimate aim to maximize an economic objective function to reduce the CO₂ emission.

2. RTO Integration with Automation Systems

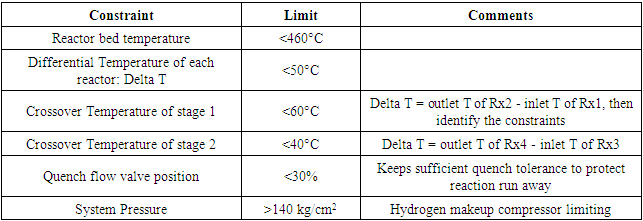
In the first place, the basic instrumentation and control layer is established for the plant by installing the distributed control system (DCS) so that all the specifications of the units are met and plant operation is stabilized and runs safely and smoothly. The next step is to implement advanced process control technologies at the plant. That control layer takes care of process constraints, interactions and future consequences of the current actions in the operation of the process units.

This control layer is called model predictive control and inferential models, which form a closed loop quality control system on the unit. The next control layer is real-time optimization, which provides a global view and incorporates different aspects and interrelations among processes in a model to compute operational decisions that optimize process efficiency and economy.

The Figure 1 shows various layers of automation integrated with real-time optimization. The refinery LP model will set the target for optimizer, which will use the steady-state and kinetic models to provide the optimized set points for a multivariable controller (MVC) to implement the processing units using a DCS as a platform. The inferential models interfacing with MVC form a closed-loop quality control system.

Figure 1. Real-time optimization integrating with the system of automation

It is also important to know that multivariable control is a pre-requisite for RTO implementation and, therefore, a good multivariable control application should be in place on the unit before planning to implement RTO project. There are two conceptual ideas, which will follow the discussions between multivariable control and RTO applications.

The multivariable control is designed in such a way that it holds the plant at constraints such as high compressor speed, column pressure drop, maximum valve position or maximum reactor temperature (run-away reaction). Nonlinear RTO models calculate optimum when it is between bounds or change position. While MVC pushes the plant to constraints, real-time optimization keeps on searching for an optimum solution, which may not be at constraints but somewhere else in the operating region of the unit.

3. Integration of Inferential Models

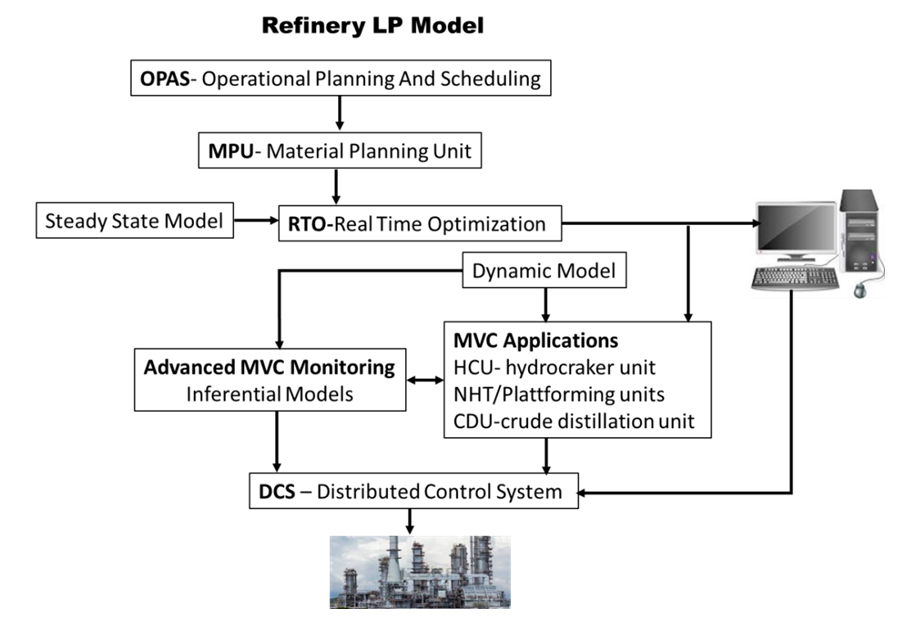
General Description

Integration of inferential models with a model-predictive control system is important as it closes the quality control loop between the two systems. The inferential models or Robust Quality Estimator (RQE) uses selected measurements (such as feed rate, temperature, pressure, etc.) to predict the real value of a critical product property or complex process variable that cannot be measured online, or is measured infrequently with potential large time delay. In a typical application, RQE provides a continuous real-time calculated value for closed loop control. It can cope with nonlinear systems, varying gains and uncertain process dynamics. This unique feature makes the model-predictive controller robust to varying process conditions and nonlinearities.

If a certain process variable is well correlated with some other particular parameters, it is assumed that the general QE equation can be written as

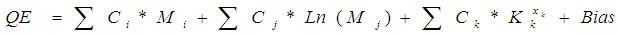Where,

QE is the estimate of the process variable

Ci, j, k are trend coefficients

Mi, j, k are measured or calculated process variables

Xk are exponentiation coefficients

Bias is a calibration constant

The different terms of the above equation represent a combination (linear with respect to the parameters) of process measurements such as pressure compensated temperature, feed flow, rundown rates, separation index terms (such as reflux, reboil or stripping steam ratios), and absolute pressure. For the flow data, the logarithmic value is often applied whereas for temperatures sometimes an exponential term is used for “contaminant” qualities such as ASTM color. In many applications the only measurements used are pressure corrected column tray or overhead temperatures.

The inferential models are regularly updated based on laboratory measurements or online analyzer. Currently, the most common approach is to correct the calibration factor bias. The RQE provides a second updating mechanism based on the Kalman filter. It will correct all the coefficients and the bias term of the regression. This makes RQE an adaptive estimator. Figure 2 gives a simplified example of the systematic approach to construct the naphtha FBP inferential model with process variables such as pressure-compensated temperature, pressure of the column and reflux ratios.

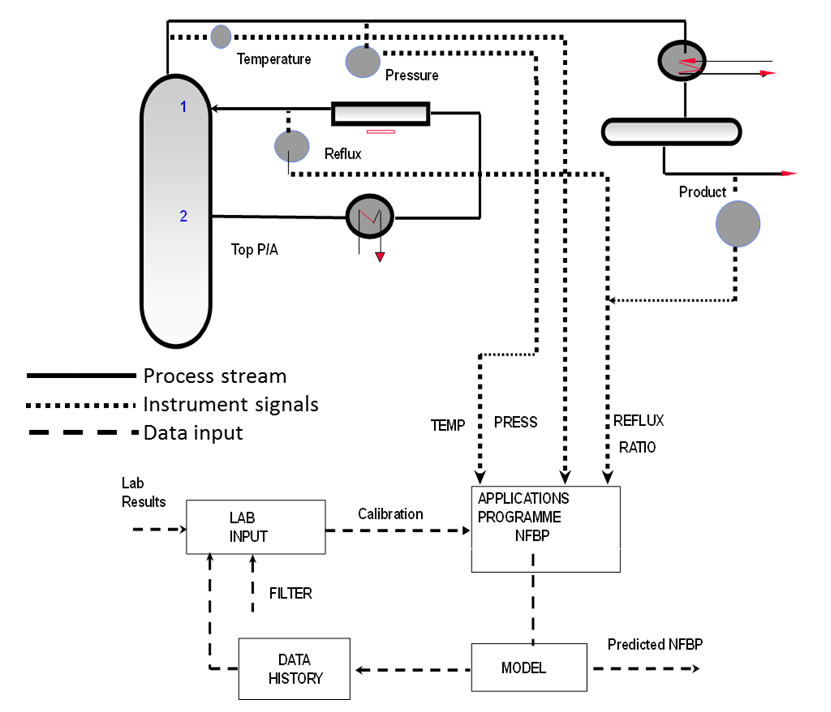Figure 2. System of inferential model and its development procedure

The model is updated using laboratory results. A system of inferential model update is shown in the lower section of Figure 2, providing laboratory result as a basis to update the predicted values and a first-order filter to compensate for the noise in the flow measurements. The average deviation from the laboratory results is only 2°C, and considering the repeatability of ± 4°C in naphtha FBP laboratory results, this prediction can be considered very accurate. The details of this system are given by Ansari and Ghazzawi [32].

4. Process Description

The hydrocracker unit (HCU) of the model case refinery has a maximum feed capacity of 27,500-28,500 barrels per stream day. The HCU consists of three major sections: reactor section, debutanizer, and main column. The operation objective of the hydrocracker unit is to maintain the feed flow at the required rate, while maximizing the gasoline or diesel yield, subject to the products qualities of the main fractionator. The key focus of RTO implementation was to provide a combination of operating conditions, which will support an increase in each reactor temperature and maximize the economic objective function to enhance the yield of gasoline or diesel products.

Therefore, raising the first stage (DHC) reactor temperature will enhance the diesel yield while raising the second stage (HC) reactor temperature will increase the gasoline yield. In total three MVC applications were identified in the site survey to achieve the goal of higher reactor conversion and yield and these applications were reactor section control; main column control and debutanizer control.

The reaction section controller is designed to meet the following process operating objectives:

1. In current operation, the fresh feed is fixed and so is the main fractionator bottom fuel oil draw of. The main objective is to maintain the higher conversion if the bottom level is controlled well. So maximizing the yield (or maximizing the Delta T) is the main economic target in this application. Which stage Delta T should be maximized that will be based on the operation mode, gasoline or diesel.

2. Stabilize the reactor temperature profile based on the operation mode.

3. Maintain the quench valve position as high limit to keep the sufficient capacity in case reactor temperature run-away reaction takes place.

5. Current Operating Strategy

The current HCU operating strategy at model case refinery can be summarized as follows:

• Maximize the unit throughput, while respecting unit constraints and required catalyst run length.

• Adjust the stage 1 or stage 2 reactor severities, to meet the requirements of two main modes, maximum naphtha or maximum diesel.

• Optimize the circulating refluxes in the product fractionator, to reduce energy costs.

The average unit stream time is 92% (including the effects of catalyst run length), which is equivalent to 336 days per year.

6. Hydrocracker Process Constraints

Table 1 gives the HCU-reactor constraints, Table 2 gives the HCU-main fractionator constraints, and Table 3 gives the main constraints on HCU-debutanizer, imposed on the controllers during the design stage. These constraints were discussed with the operations on the reactor systems to keep the reactor bed temperature within the specified limits and to keep significant quench tolerance to protect run-away reaction.

Table 1. Hydrocracker Reactor Constraints

Table 2. Main Fractionator Constraints

Table 3. The Debutanizer main constraints

7. Steps of Online Closed-loop Optimization

The following is a simplified description of the steps of operations involved in online closed-loop optimizations: the data reconciliation; rating case, base case; constraint calculation; optimization case and implementation. Figure 3 shows these steps starting from steady-state detection to implementation – downloading the targets to the control system.

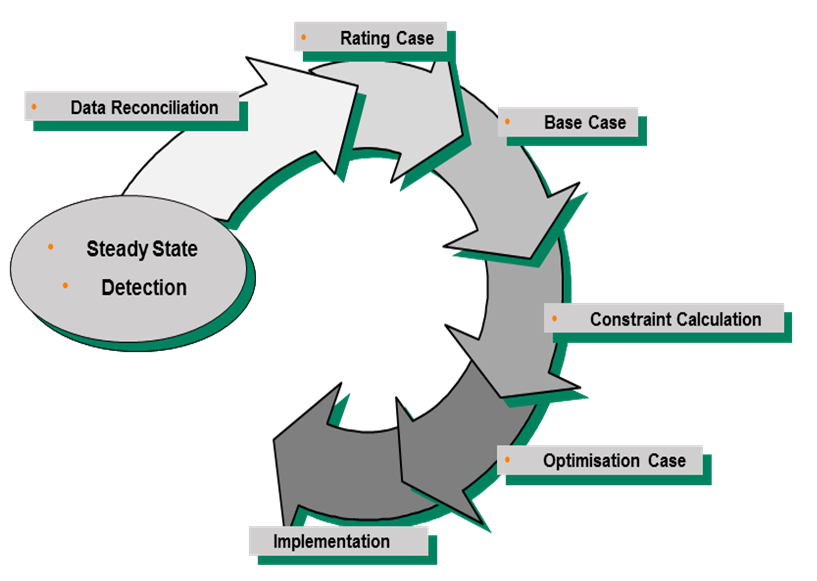Figure 3. Steps of online closed loop optimization

8. Steady-state Detection (SSD)

The steady-state detection has a great influence on RTO performance but is not discussed in detail in the RTO literature. In the current RTO application, the “statistical method” of steady-state detection is discussed as follows: The total variance of a signal x for a data window with n points is given by the sample variance (s²) according to:

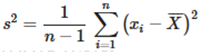Where X is the sample mean, while the variance of the difference between two successive points is expressed by:

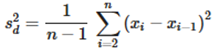These two variances give rise to the statistic R, which is eventually expressed as C, defined as:

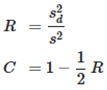There is an extra option, where the user may define a tuning parameter, T_SM, which changes the definition of R in the following way:

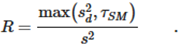Then, the signal is static if R is greater than a critical value Rc (or if C is lower than a critical value Cc).

9. Data Reconciliation

Data reconciliation involves mass and heat balances around each and every piece of equipment in the unit, which is fully consistent with the overall balances [34]. The benefits include consistency and accuracy of yield calculations and targeted instrument maintenance. When data present significant uncertainty, data reconciliation is the first step to be applied in a model-based approach to process optimization. The target is to estimate consistent values of all plant variables from available online measurements based on a process model. Soderstrom et al. [35] highlighted that if measurement errors resulting from poor instrument calibration are not considered, the data reconciliation step or subsequent parameter estimation step will not provide meaningful answers.

The redundancy in measurements is required by data reconciliation system. Therefore, it is important to have accurate, consistent and robust estimations so that modelling errors may be minimized, irrespective of process disturbances, measurement noise, etc. It also updates certain unknown model parameters.

The combination of RTO and regulatory control can be considered similar to cascade control system as shown in Figure 4. The outer RTO loop will operate more slowly than the inner loop, and a poor design of this interaction will result in poor performance. The dynamic controller handles the transformation between the steady-state model used in RTO and the actual dynamic operation of the process. If the RTO model and dynamic model have very different gains, the resulting combination can perform poorly. As in cascade control, the inner loop should be faster than the outer loop; otherwise poor closed-loop performance may result [36].

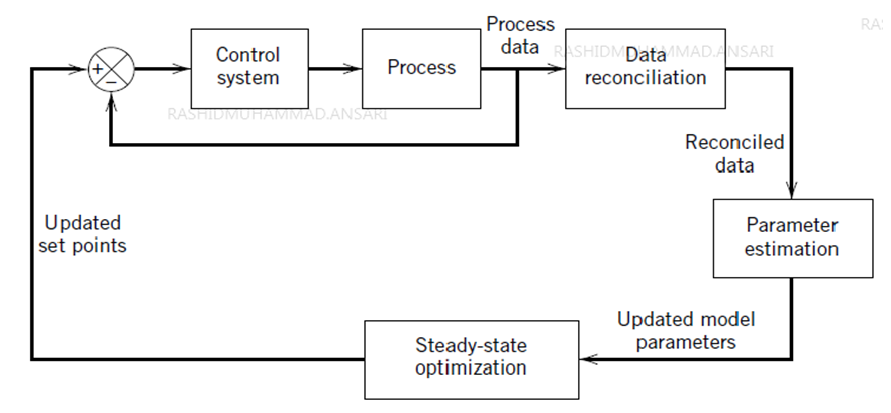Figure 4. A block diagram representing the RTO and regulatory feedback system

In the rating case the rating of the equipment is identified and in the base case the economic objective function is introduced and measurement offsets are calculated. The benefits of these steps include online calculations of unit margin and additional targeted instrumentation maintenance.

The constraint calculations include equipment constraints, control constraints, process constraints and economic constraints. The benefits of this step includes active constraint tracking and focused debottlenecking. In optimization step, the effect of multiple independents is observed on economic objective functions to achieve the maximum profit and, finally, the targets of optimized solutions are downloaded in the implementation step.

10. Application of RTO to Reduce CO₂ Emission

The following steps would be required to apply real-time Optimization application on the refinery processes to reduce CO₂ emissions.

• Developing the process models for all the potential units with CO₂ emissions

• Integration of RTO with MPC to optimize the operation

• Integrating CO₂ inferential models with MPC

• Maximizing economic objective function with a CO₂ emission level constraint

• Improving energy efficiency to reduce the overall CO₂ emissions

The RTO application on CO₂ emissions reduction would first require modelling refinery processes to identify promising units with higher emissions to be targeted for CO₂ reduction in the refinery. At the same time, tools for achieving CO₂ emissions reduction will be developed for two different approaches: improvement of energy efficiency and application of CO₂ capture and conversion technologies.

Among the refinery processes, it has been identified that units with larger furnace systems, such as a crude oil distillation unit, are the most energy intensive processes in the refinery; fouling of the heat exchanger leads to increases in the operating cost and carbon emission. In addition, a majority of energy input to hydrocracking and catalytic reforming is in burning coke off the catalyst and catalyst regeneration respectively. Meanwhile, the hydrogen production generates a large amount of CO₂ by the method of steam methane reforming, which is the most common reaction for the hydrogen production.

To solve the problem for CO₂ reduction in the typical refinery process, the multivariable control applications need to be developed on various potential units of the refinery to achieve CO₂ reduction. The model-predictive or multivariable control has already been implemented in one of the refineries in the Middle East on a crude distillation unit [37,38,39], on a catalytic reforming unit [40,41], and on a hydrocracking unit [42].

The multivariable control applications on these units are forming closed-loop quality control systems with the inferential models [43,44]. The multivariable control applications on these units may be modified to include CO₂ variable in the controller design. In addition, an inferential model for CO₂ would be required to be developed to form a closed-loop control system [32]. Real-time optimization applications will be required to be extended to other processing units with larger emissions of CO₂ such as crude distillation and catalytic reforming. Edgar et al. [45] have listed six steps that should be used in solving any practical optimization problems. A summary of the procedure with comments related to RTO is given below:

Step 1. Identify the process variables. The important input and output variables for the process must be identified. These variables are employed in the objective function and the process model.

Step 2. Select the objective function. To arrive at a single objective function based on operating profit, the quantity and quality of each product must be related to the consumption of utilities and the feedstock composition. The specific objective function selected may vary depending on plant configuration as well as the supply/demand situation.

Step 3. Develop the process model and constraints. Steady-state process models are formulated, and operating limits for the process variables are identified. The process model can be based on the physics and chemistry of the process or it can be based on empirical relations obtained from experimental process data. Inequality constraints arise because many physical variables, such as composition or pressure, can only have positive values; or there may be maximum temperature or maximum pressure restrictions. These inequality constraints are a key part of the optimization problem statement and can have a profound effect on the optimum operating point. In most cases, the optimum lies on a constraint.

Step 4. Simplify the model and objective function. Before undertaking any computation, the mathematical statement developed in steps 1-3 may be simplified to be compatible with the most effective solution techniques. A nonlinear objective function and nonlinear constraints can be linearized to use a fast, reliable optimization method such as linear programming.

Step 5. Compute the optimum. This step involves choosing an optimization technique and calculating the optimum set points to be implemented by model-predictive controller. Most of the literature on the subject of optimization is concerned with this step such as developing efficient and robust numerical methods for optimization calculations [60].

Step 6. Perform sensitivity studies. It is useful to know which parameters offer an optimization problem and are the most important in determining the optimum. By varying model and cost parameters individually and recalculating the optimum, the most sensitive parameters can be identified.

11. Results & Discussion

In relation to the benefits of RTO implementation on model case refinery in the Middle East, it was observed that benefits obtained mainly from reactors weighted average bed temperature (WABT) independent variables. The WABT set points were implemented at each run and reached by the multivariable control applications. The feeds were limited by the constraints but contributed at the profit. The main fractionator was the most constraining factor, mainly in the LDO and HDO sections. The benefits were achieved without compromising run length and have been obtained by maintaining the WABT and varying the operating conditions to improve product values.

It was one of the findings from RTO simulation data that by decreasing the indirect recycle flow (IDR) from 50 m³/hr to 48 m³/hr, substantial benefits can be achieved through higher unit margins and these economic gains are maximum when HDO rundown flow is unconstrained. In general, the RTO benefits come from the following improvements:

1. Improve the yield of high value products by maximizing the economic objective function to maximize diesel or gasoline on the hydrocracker.

2. Increase the federate subject to unit constraints and catalyst run length.

3. Adjust the bed inlet temperature to maintain a desired WABT and protects against constraints such as hydrogen quench and delta temperature limits.

4. Improve catalyst life by maintaining the reactor bed temperature profile.

The development and implementation of RTO systems for the hydrocracking unit was an outcome of great team work and collaboration between industrial and vendor teams over a couple of years. This has brought substantial benefits to the operation of the refinery. It has increased the production of high value products such as diesel and gasoline by maximizing the economic objective functions, using RTO techniques.

The Figure 5 shows the inferential model of gasoline, 95% point of heavy naphtha (similar model was developed for LN 95%) compared with the laboratory results in main fractionator of Hydrocracker unit which was developed using inferential modelling techniques and formed a quality control system with model predicticve control and integrated with RTO to maximize the yield of gasoline as shown in Figure 6 [42].

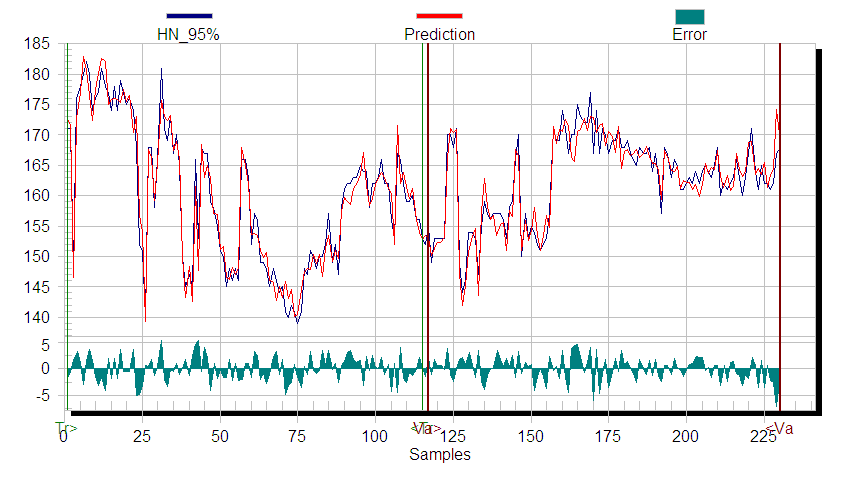Figure 5. Inferential model for gasoline (HN 95% - hydrocracking)

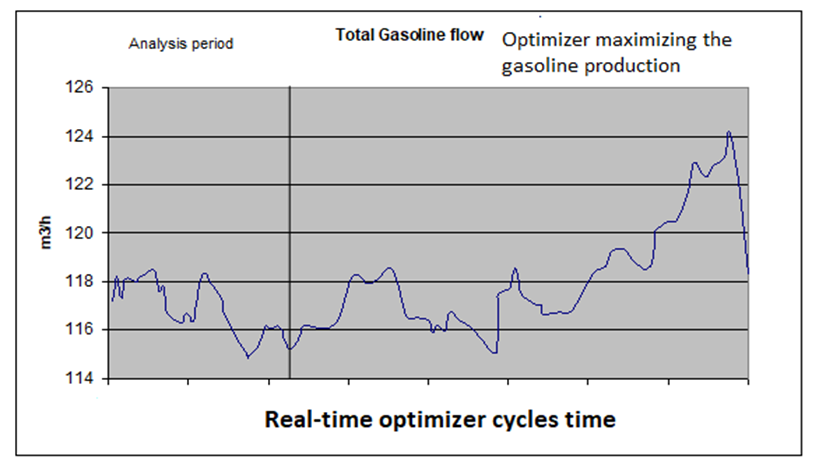Figure 6. Maximization of gasoline production with RTO application

12. Diesel 90% Specification Control

The objective of HDO90% control is to keep the quality of HDO90% within the specified range using the model predictive control and inferential model in a closed-loop control system. The Figure 7 shows that the diesel (HDO90%) is well controlled between the limits 350-352C. RTO maximizes the diesel when it is accurately controlled between these limits [42].

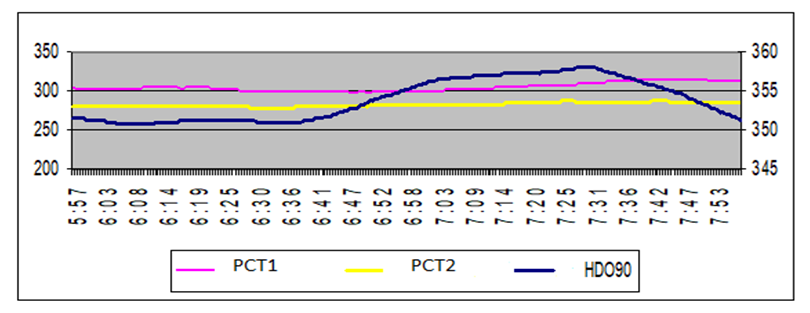Figure 7. Diesel (HDO 90%) specification control between the limits (350-352C)

The optimized-based study of CO₂ reduction strategies in the refinery is currently undertaken which will bring together other processes to form a large-scale optimization solution to enhance the performance of all the processing units in the refinery.

It was also observed during implementation phase that the reliable instrumentation is the key to success of RTO. This includes the necessary support infrastructure, to ensure that any instrument faults identified during design and commissioning are quickly and effectively rectified.

It is important to have reliable inferential models and it is equally important that these quality indicators continue to perform effectively. These inferential models will help significantly with the success of the optimization-based study for CO₂ emission reduction in the refineries.

13. Conclusions

The RTO of the hydrocracker was implemented successfully. The integration of RTO with multivariable control applications and inferential models brought substantial benefits to the hydrocracker operation. The main benefits of RTO implementation were achieved from the reactor’s WABT independent variables. These set points were implemented at each run and were reached by MVC. The feeds were limited by the constraints but contributed at the profit. The main fractionator operation was the most constraining factor, mainly in the LDO and HDO sections. These benefits have been achieved without compromising the catalyst run length.

It is also envisaged that implementing RTO applications for CO₂ emissions reduction would bring higher benefits to the refinery. Since the applications of multivariable control are already in place on the key processing units of the refinery, the implementation of RTO will help to drive the plant operation toward the optimum operation by maximizing the economic objective functions on these processing units.

ACKNOWLEDGEMENTS

The authors wish to express their gratitude to the refinery’s RTO team members: process engineers, operation engineers, hydrocracker operators and foremen for their participation on this project. Many thanks to R&DC management for providing us this great opportunity to work on the RTO project for CO₂ emissions reduction in the refinery.