-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2019; 9(2): 45-55
doi:10.5923/j.control.20190902.03

Observer-Based Robust Adaptive Fuzzy Control for Uncertain Underactuated Systems with Time Delay and Dead-Zone Input
Chiang-Cheng Chiang, Li-Chung Chang
Department of Electrical Engineering, Tatung University, Taipei, Taiwan, Republic of China
Correspondence to: Chiang-Cheng Chiang, Department of Electrical Engineering, Tatung University, Taipei, Taiwan, Republic of China.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper investigates the observer-based robust adaptive fuzzy control problem for a class of uncertain underactuated systems with time delay and dead-zone input. Within this method, the state observer is developed for estimating the unmeasured states in the underactuated system. The fuzzy logic systems are used to approximate the unknown nonlinear functions, and some adaptive laws are introduced to estimate unknown parameters. The dead-zone input which is one of the significant input constraints often exists in many practical industrial control systems. By employing a Lyapunov-Krasovskii functional, it is verified that the proposed controller ensures that all the signals in the closed-loop system are bounded. Simulation results are illustrated to demonstrate the regulation performance of the system output and state estimation by the proposed control method.
Keywords: Underactuated system, Lyapunov-Krasovskii functional, Dead-zone input, Fuzzy logic systems, State observer, Time delay
Cite this paper: Chiang-Cheng Chiang, Li-Chung Chang, Observer-Based Robust Adaptive Fuzzy Control for Uncertain Underactuated Systems with Time Delay and Dead-Zone Input, International Journal of Control Science and Engineering, Vol. 9 No. 2, 2019, pp. 45-55. doi: 10.5923/j.control.20190902.03.
Article Outline
1. Introduction
- In the past decades, the control problem of underactuated systems has received a lot of attention. The underactuated system is a mechanical system with fewer control actuators than degrees of freedom and can be found in many applications, such as boom cranes [1], axisymmetric spacecrafts [2], pole and hoop systems [3], surface vessels [4], and so on. The underactuated systems have some advantages like decreasing the number of actuators, reducing the cost, and lightening the system.The dead-zone input nonlinearity is a nonsmooth function that features certain insensitivity for small control inputs which is often encountered in a variety of practical systems, such as the valve system [5] and the gripper rotating system [6]. The adaptive fuzzy controller is proposed to deal with nonlinear systems with unknown dead zones [7]. In [8], the adaptive tracking control problems are considered for a class of nonlinear systems with a fuzzy dead-zone input.A category of switched uncertain nonlinear systems were studied through using adaptive fuzzy output-feedback control in [9]. In [10], a robust adaptive fuzzy tracking controller was designed for pure-feedback stochastic nonlinear systems with input constraints. On the other hand, Zhou et al. [11] deal with the problem of adaptive fuzzy control for nonstrict-feedback systems with input saturation and output constraint. In this paper, fuzzy logic systems are introduced to describe the input/output behavior of the controlled system. Based on fuzzy logic systems, we design the adaptive fuzzy controllers with several appropriate adaptive laws.In many practical systems, system states are not available for measurement. Based on state variable filters, an observer is presented for solving the problem of the unavailable states of the system. Recently, for a class of uncertain nonlinear systems with nonsymmetric input saturation, the problem of observer-based adaptive NN control was considered in [12]. In [13], a fuzzy state observer was proposed to estimate the unmeasured states.It is well known that the time-delay systems have received considerable attention [14], [15], and the existence of time delay often leads to the system instability and poor performance. Based on Lyapunov-Krasovskii functional, the presented robust adaptive fuzzy control method can ensure the robust stability of the whole closed-loop nonlinear system with time delay.In this paper, we focus on developing an observer-based robust adaptive fuzzy control method for uncertain underactuated system with time delay and dead-zone input. Fuzzy logic systems are introduced to approximate unknown nonlinear functions, and a fuzzy state observer is constructed to estimate the unmeasurable system states. Some appropriate adaptive laws are used to estimate the upper bounds of the unknown uncertainties. Finally, with the help of Lyapunov stability theorem, the proposed controller can guarantee the stability of the system. The rest of this paper is organized as follows. The description of the system and the concept of fuzzy logic systems are presented together in Section II. The observer-based robust adaptive fuzzy controller is designed in Section III for uncertain underactuated system with time delay and dead-zone input. In Section IV, the numerical example and the practical example are provided to validate the effectiveness of the proposed observer-based robust adaptive fuzzy control approach. Section V contains the conclusion.
2. Problem Statement and Preliminaries
2.1. System Description
- Consider a class of single-input multi-output uncertain underactuated nonlinear systems with time delay and dead- zone input expressed as follows:
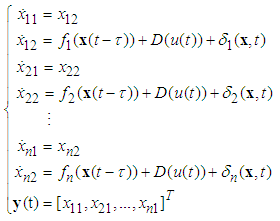 | (1) |
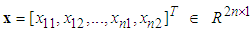 is the system state vector which is assumed to be unavailable for measurement,
is the system state vector which is assumed to be unavailable for measurement, 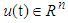 and
and 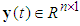 are the input and output of the system, respectively.
are the input and output of the system, respectively. 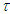 is the value of time delay
is the value of time delay 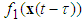 ,
,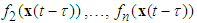 are unknown real continuous nonlinear functions, and
are unknown real continuous nonlinear functions, and 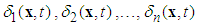 are the unknown bounded disturbances.
are the unknown bounded disturbances. 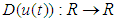 is the nonlinear input function containing a dead zone.Assumption 1: The time delay
is the nonlinear input function containing a dead zone.Assumption 1: The time delay 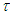 is a fixed and known positive constant.System (1) can be rewritten as
is a fixed and known positive constant.System (1) can be rewritten as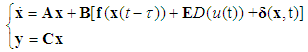 | (2) |

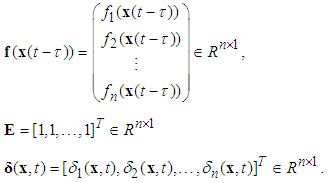
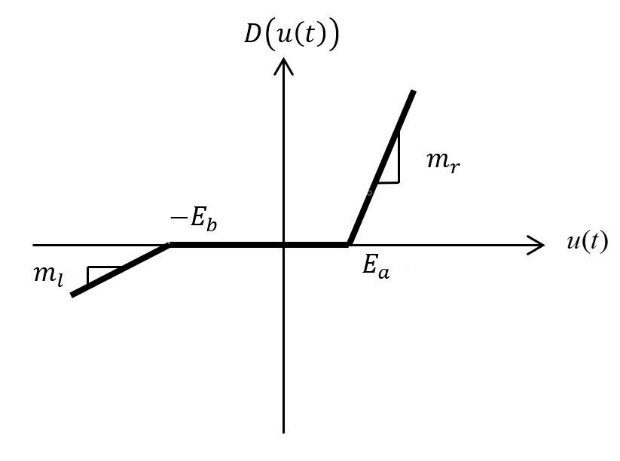 | Figure 1. Dead-zone model |
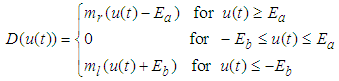 | (3) |
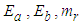 and
and 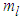 are parameters and slopes of the dead zone, respectively.To investigate the key features of the dead zone in the control problems, the following common assumptions are given.Assumption 2: The dead-zone output
are parameters and slopes of the dead zone, respectively.To investigate the key features of the dead zone in the control problems, the following common assumptions are given.Assumption 2: The dead-zone output 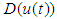 is not available to obtain.Assumption 3: The coefficients
is not available to obtain.Assumption 3: The coefficients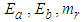 and
and 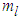 are unknown.Assumption 4: There exist known constants
are unknown.Assumption 4: There exist known constants 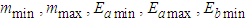 and
and 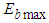 such that the unknown dead-zone parameters
such that the unknown dead-zone parameters 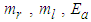 and
and 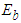 are bounded, i.e.
are bounded, i.e. 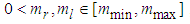 ,
, 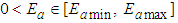 ,
, 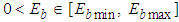 .Based on the above assumptions, the expression (3) can be rewritten as
.Based on the above assumptions, the expression (3) can be rewritten as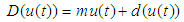 | (4) |
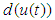 can be calculated from (3) and (4) as
can be calculated from (3) and (4) as 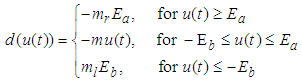 | (5) |
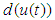 is bounded, and satisfies:
is bounded, and satisfies: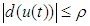 | (6) |
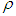 is the upper bound, which can be chosen as
is the upper bound, which can be chosen as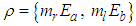 | (7) |
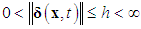 , where h is an unknown constant.Control objective: The control objective is to design a robust adaptive fuzzy controller
, where h is an unknown constant.Control objective: The control objective is to design a robust adaptive fuzzy controller 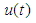 to ensure that all the closed-loop signals are bounded.
to ensure that all the closed-loop signals are bounded.2.2. Description of Fuzzy Logic Systems
- The fuzzy logic system performs a mapping from
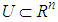 to
to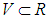 . Let
. Let 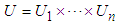 where
where 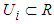 ,
, 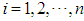 . The fuzzy rule base consists of a collection of fuzzy IF-THEN rules:
. The fuzzy rule base consists of a collection of fuzzy IF-THEN rules: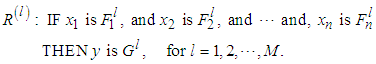 | (8) |
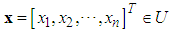 and
and 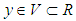 are the input and output of the fuzzy logic system,
are the input and output of the fuzzy logic system, 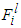 and
and 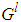 are fuzzy sets in
are fuzzy sets in 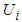 and
and 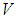 , respectively. The fuzzifier maps a crisp point
, respectively. The fuzzifier maps a crisp point 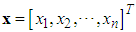 into a fuzzy set in
into a fuzzy set in 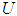 .The fuzzy systems with center-average defuzzifier, product inference and singleton fuzzifier are of the following form:
.The fuzzy systems with center-average defuzzifier, product inference and singleton fuzzifier are of the following form: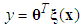 | (9) |
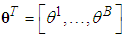 with each variable
with each variable 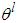 as the point at which the fuzzy membership function of
as the point at which the fuzzy membership function of 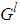 achieves the maximum value and
achieves the maximum value and 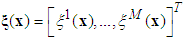 with each variable
with each variable 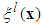 as the fuzzy basis function defined as
as the fuzzy basis function defined as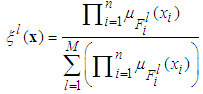 | (10) |
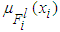 is the membership function of the fuzzy set.
is the membership function of the fuzzy set.3. Controller Design and Stability Analysis
3.1. Observer Design
- First, the following fuzzy logic systems can be constructed, over a compact set
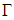 , the unknown nonlinear functions
, the unknown nonlinear functions  can be approximated as
can be approximated as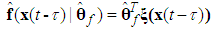 | (11) |
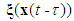 is the fuzzy basis vector,
is the fuzzy basis vector, 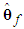 is the corresponding adjustable parameter vector of the fuzzy logic system.Because the system states are assumed to be unmeasurable in this paper, the fuzzy logic systems (11) cannot be directly used for the unknown nonlinear system. Therefore, an observer is designed to estimate the unmeasurable system states. Let us define that
is the corresponding adjustable parameter vector of the fuzzy logic system.Because the system states are assumed to be unmeasurable in this paper, the fuzzy logic systems (11) cannot be directly used for the unknown nonlinear system. Therefore, an observer is designed to estimate the unmeasurable system states. Let us define that 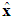 is the estimate of
is the estimate of 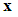 at first. Then, the following fuzzy logic systems can be obtained as
at first. Then, the following fuzzy logic systems can be obtained as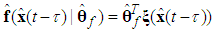 | (12) |
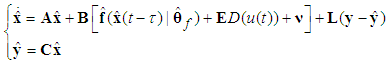 | (13) |
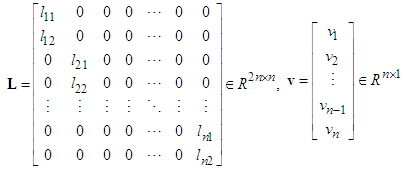
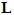 is the observer gain matrix to guarantee the characteristic polynomial of
is the observer gain matrix to guarantee the characteristic polynomial of 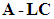 to be Hurwitz. The estimation error vector is defined as
to be Hurwitz. The estimation error vector is defined as 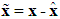 and
and 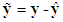 , then according to (2) and (13), one has
, then according to (2) and (13), one has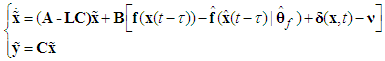 | (14) |
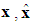 , and
, and 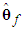 belong to compact sets
belong to compact sets 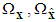 , and
, and 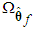 respectively, which is defined as
respectively, which is defined as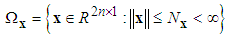 | (15) |
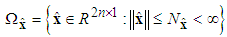 | (16) |
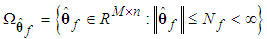 | (17) |
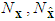 , and
, and  are the designed parameters, and M is the number of fuzzy inference rules. Let us define the optimal parameter vector
are the designed parameters, and M is the number of fuzzy inference rules. Let us define the optimal parameter vector 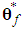 as follows:
as follows: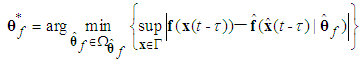 | (18) |
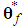 is bounded in the suitable closed set
is bounded in the suitable closed set 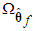 .The parameter estimation errors can be defined as
.The parameter estimation errors can be defined as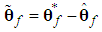 | (19) |
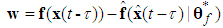 | (20) |
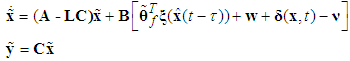 | (21) |
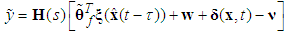 | (22) |
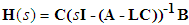 and s denotes the complex Laplace transform variable. As previously discussed in this chapter, not all elements of
and s denotes the complex Laplace transform variable. As previously discussed in this chapter, not all elements of 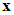 could be obtained, because not all the system states are available for measurement. Consequently, one could not obtain all elements of
could be obtained, because not all the system states are available for measurement. Consequently, one could not obtain all elements of 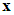 . The state variable filters [17] will be introduced to cope with this problem. The stable filter
. The state variable filters [17] will be introduced to cope with this problem. The stable filter 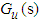 is chosen as follows:
is chosen as follows: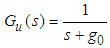 | (23) |
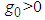
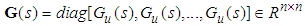 | (24) |
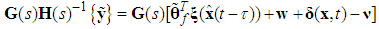 | (25) |
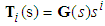 ,
,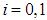 , thus,
, thus,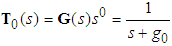 | (26) |
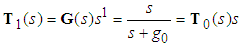 | (27) |
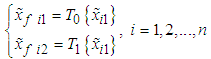 | (28) |
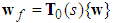 | (29) |
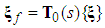 | (30) |
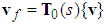 | (31) |
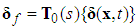 | (32) |
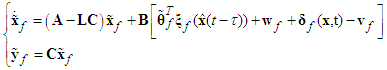 | (33) |
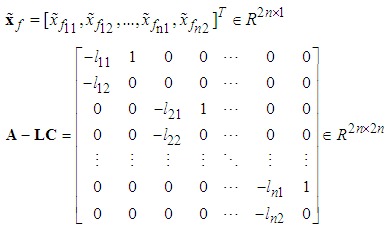 It is assumed that there exists an unknown constant
It is assumed that there exists an unknown constant 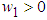 , such that
, such that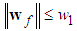 | (34) |
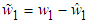 | (35) |
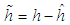 | (36) |
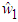 and
and 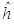 are the estimates of
are the estimates of 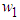 and h, respectively.Based on Lyapunov stable theorem, the robust compensation term
and h, respectively.Based on Lyapunov stable theorem, the robust compensation term 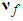 and the parameter update laws can be obtained as follows:
and the parameter update laws can be obtained as follows: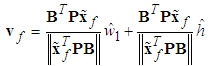 | (37) |
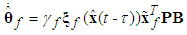 | (38) |
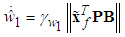 | (39) |
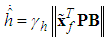 | (40) |
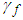 ,
, 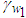 , and
, and 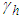 are positive constantsRemark 1: Without loss of generality, the adaptive laws used in this paper are assumed that the parameter vectors are within the constraint sets or on the boundaries of the constraint sets but moving toward the inside of the constraint sets. If the parameter vectors are on the boundaries of the constraint sets but moving toward the outside of the constraint sets, we must use the projection algorithm to modify the adaptive laws such that the parameter vectors will remain inside of the constraint sets. Readers can refer to reference [16]. The proposed adaptive law (38) can be modified as the following form:
are positive constantsRemark 1: Without loss of generality, the adaptive laws used in this paper are assumed that the parameter vectors are within the constraint sets or on the boundaries of the constraint sets but moving toward the inside of the constraint sets. If the parameter vectors are on the boundaries of the constraint sets but moving toward the outside of the constraint sets, we must use the projection algorithm to modify the adaptive laws such that the parameter vectors will remain inside of the constraint sets. Readers can refer to reference [16]. The proposed adaptive law (38) can be modified as the following form: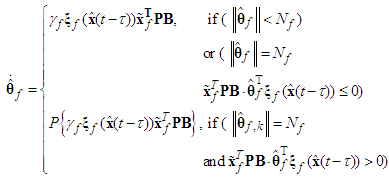 | (41) |
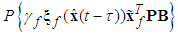 is defined as
is defined as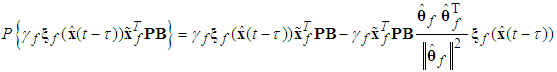 | (42) |
 , if there exists a symmetric positive definite matrix
, if there exists a symmetric positive definite matrix  such that the following Lyapunov equation
such that the following Lyapunov equation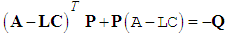 | (43) |
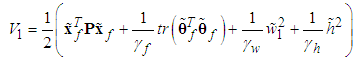 | (44) |
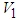 and the facts
and the facts 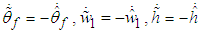 one has
one has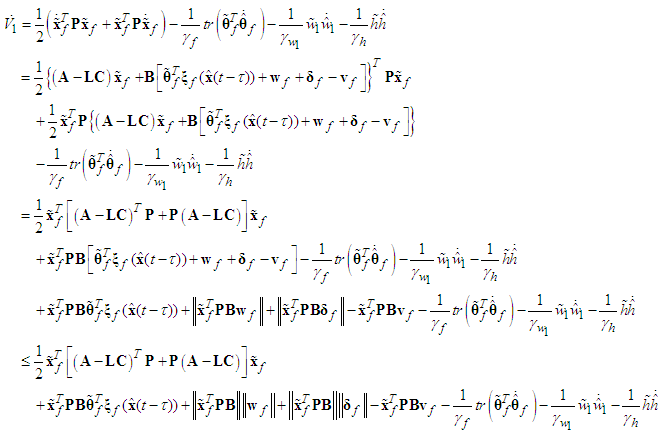 | (45) |
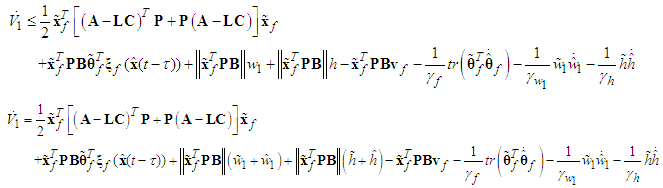 | (46) |
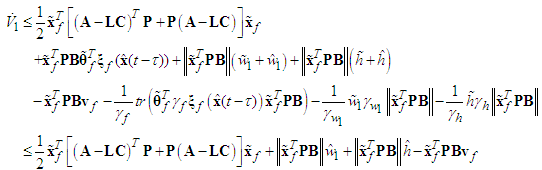 | (47) |
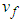 (37), the above equation can be rewritten as
(37), the above equation can be rewritten as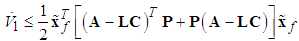 | (48) |
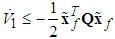 | (49) |
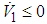 from (49), and the estimation errors of the closed-loop system converges asymptotically to a neighborhood of zero based on Lyapunov synthesis approach. This completes the proof.
from (49), and the estimation errors of the closed-loop system converges asymptotically to a neighborhood of zero based on Lyapunov synthesis approach. This completes the proof.3.2. Controller Design
- Based on Lyapunov stable theorem, the observer-based controller
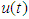 is given by
is given by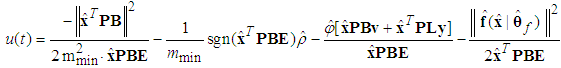 | (50) |
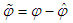 | (51) |
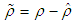 | (52) |
 is the estimate of
is the estimate of 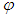 , which is defined as
, which is defined as 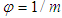 .
. 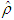 is the estimate of
is the estimate of 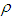 . The parameter update laws are as follows:
. The parameter update laws are as follows: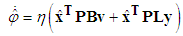 | (53) |
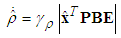 | (54) |
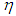 and
and 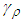 are positive constants, and
are positive constants, and 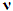 can be obtained by backward from
can be obtained by backward from 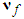 .Theorem 2: Consider the single-input multi-output uncertain underactuated system with time delay and dead-zone input (1). The proposed observed-based robust adaptive fuzzy controller defined by (50) guarantees that all signals of the closed-loop system are bounded and converge to a neighborhood of zero.Proof: Consider the Lyapunov function candidate
.Theorem 2: Consider the single-input multi-output uncertain underactuated system with time delay and dead-zone input (1). The proposed observed-based robust adaptive fuzzy controller defined by (50) guarantees that all signals of the closed-loop system are bounded and converge to a neighborhood of zero.Proof: Consider the Lyapunov function candidate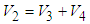 | (55) |
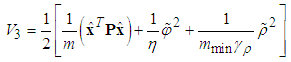 | (56) |
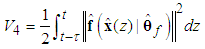 | (57) |
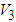 and the facts
and the facts 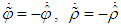 yields
yields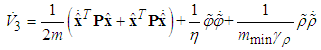 | (58) |
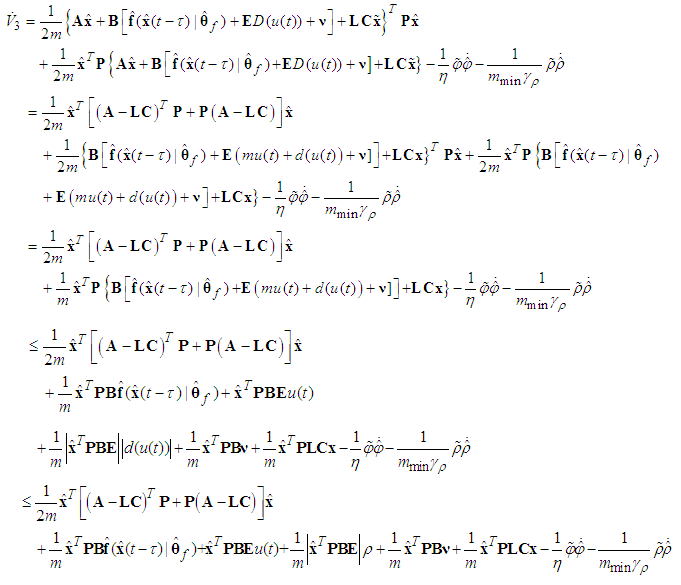 | (59) |
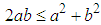 , Eq. (59) can be rewritten as
, Eq. (59) can be rewritten as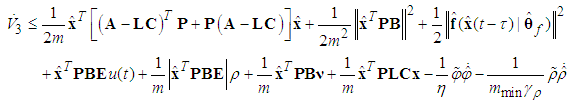 | (60) |
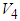 with respect to time, one gets
with respect to time, one gets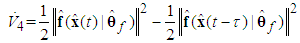 | (61) |
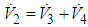 , one has
, one has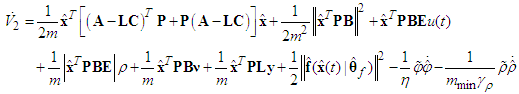 | (62) |
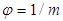 and Assumption 4, Eq. (3.54) becomes
and Assumption 4, Eq. (3.54) becomes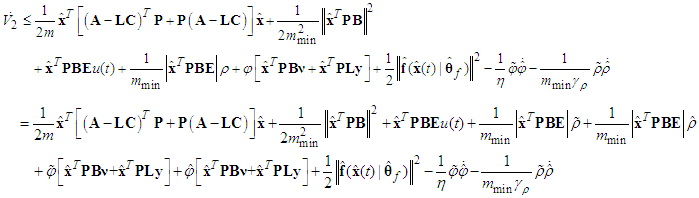 | (63) |
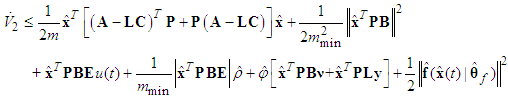 | (64) |
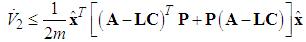 | (65) |
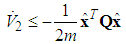 | (66) |
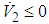 from (66), and the all signals of the closed-loop system converge asymptotically to a neighborhood of zero based on the Lyapunov synthesis approach. This completes the proof.Remark 2: Because the discontinuities in the control term (50) give rise to chatter in the system, it has been proposed that
from (66), and the all signals of the closed-loop system converge asymptotically to a neighborhood of zero based on the Lyapunov synthesis approach. This completes the proof.Remark 2: Because the discontinuities in the control term (50) give rise to chatter in the system, it has been proposed that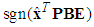 will be replaced by a continuous approximation in an
will be replaced by a continuous approximation in an 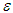 -width region of
-width region of 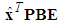 . Thus, replacing
. Thus, replacing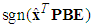 with
with 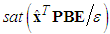 in (50), the
in (50), the 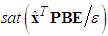 is described by
is described by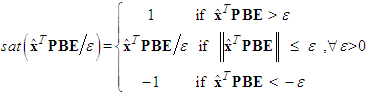 | (67) |
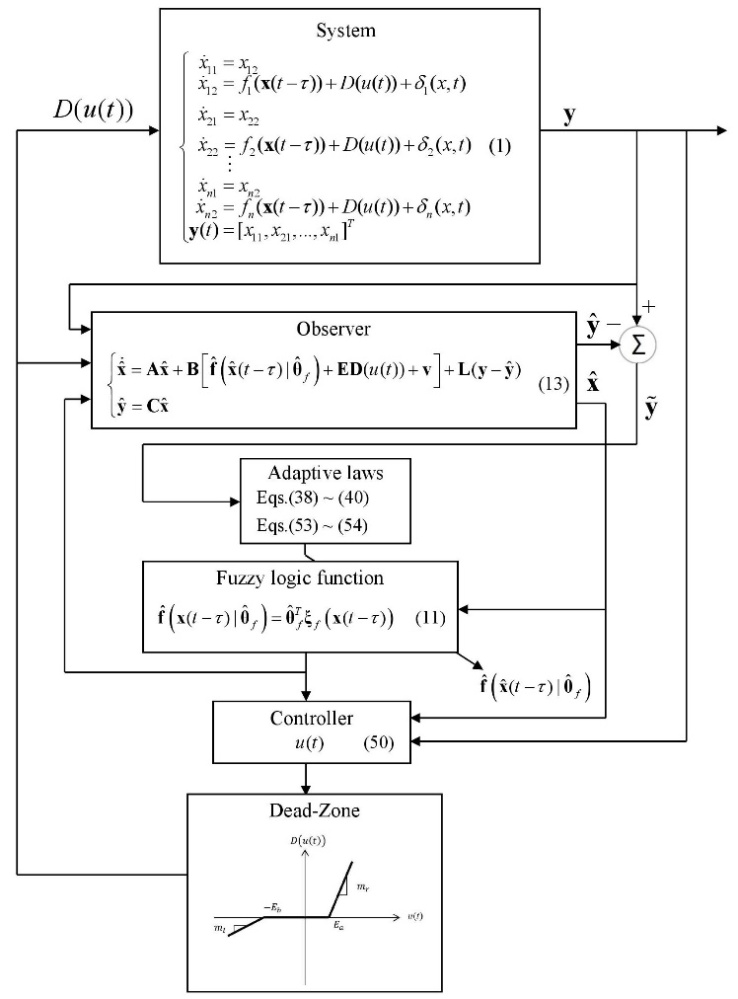 | Figure 2. The block diagram of the proposed control system |
4. An Example and Simulation Results
- In this section, a series of simulation results of a underactuated nonlinear system and a underactuated mass-spring-damper system are used to demonstrate the effectiveness of the proposed controller.Example 1: An Underactuated Nonlinear SystemConsider the underactuated nonlinear system:
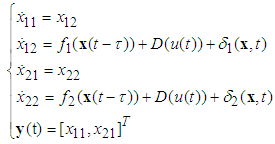 | (68) |
 are the displacements of the masses.
are the displacements of the masses.  are the velocities of the masses.
are the velocities of the masses.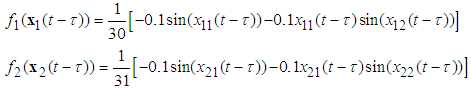
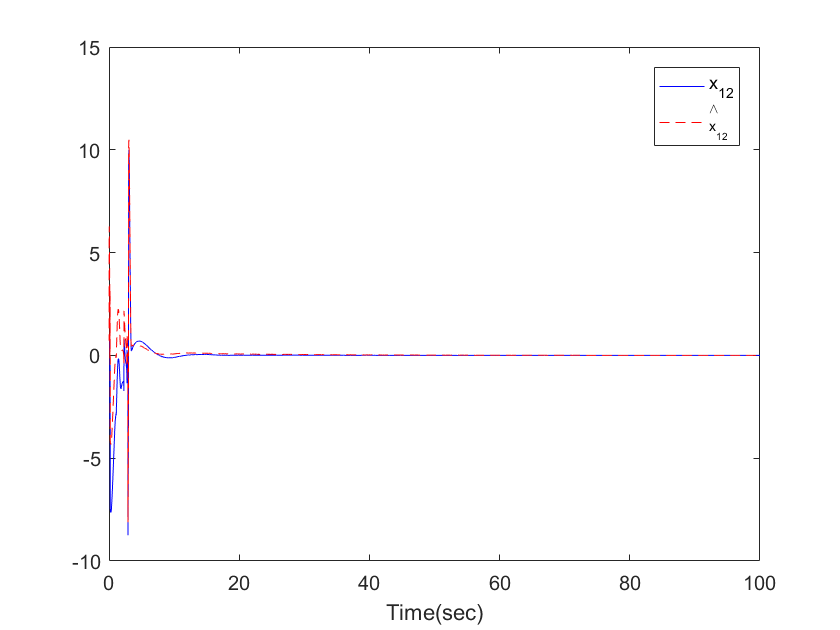
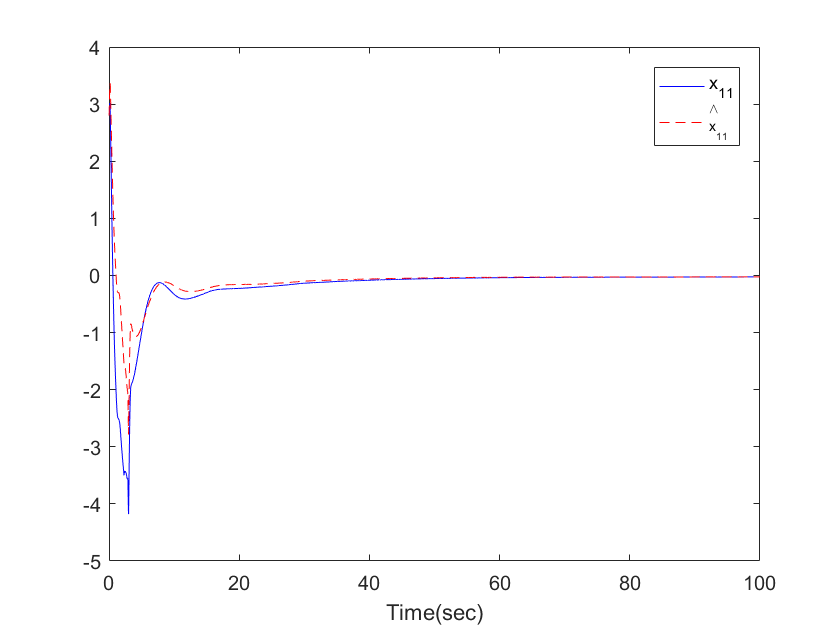 | Figure 3. The trajectories of  and and  for Example 1 for Example 1 |
 | Figure 4. The trajectories of 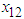 and and 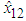 for Example 1 for Example 1 |
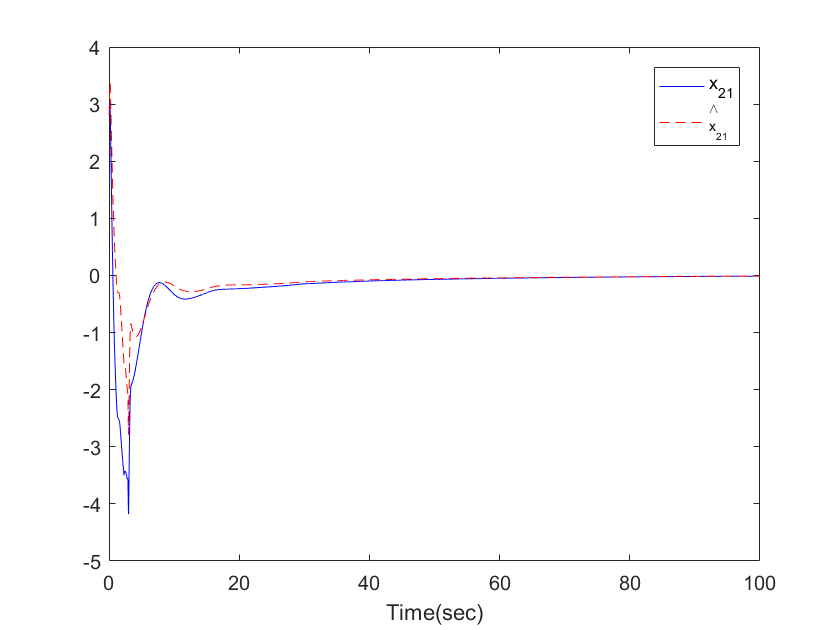 | Figure 5. The trajectories of 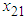 and and 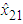 for Example 1 for Example 1 |
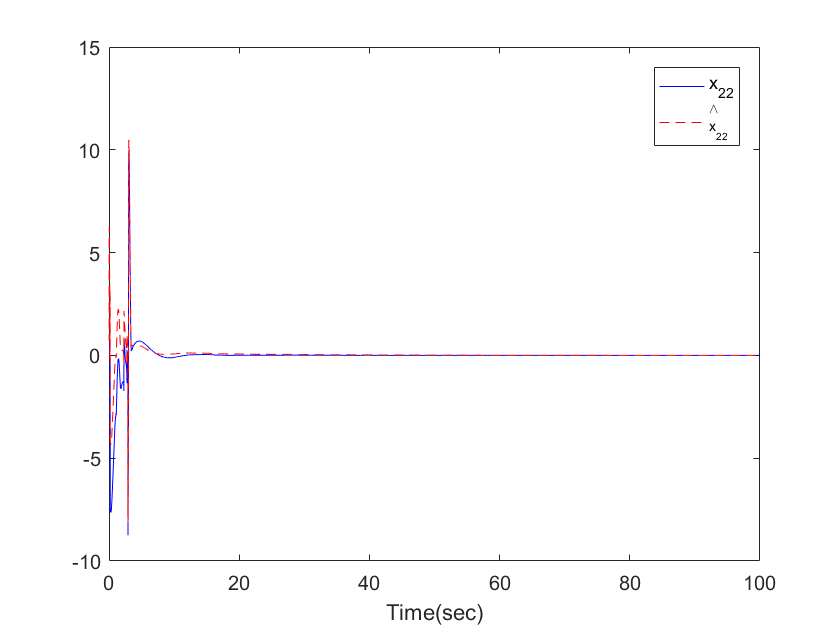 | Figure 6. The trajectories of 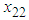 and and 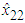 for Example 1 for Example 1 |
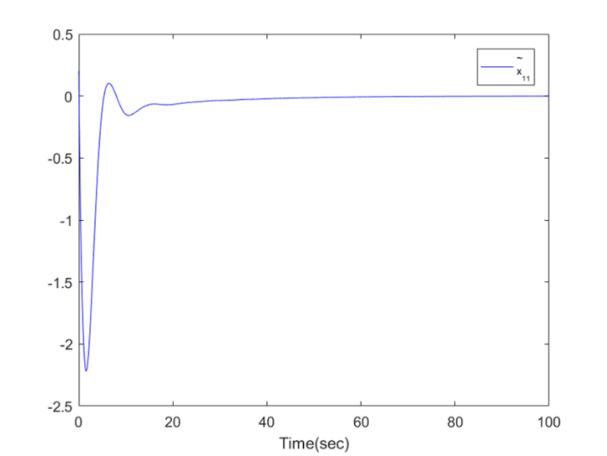 | Figure 7. The trajectory of 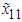 for Example 1 for Example 1 |
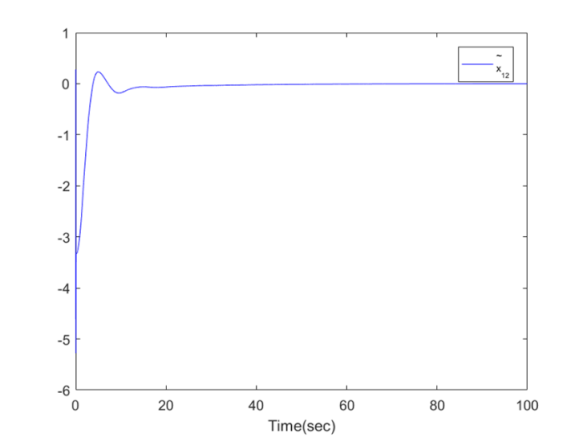 | Figure 8. The trajectory of 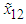 for Example 1 for Example 1 |
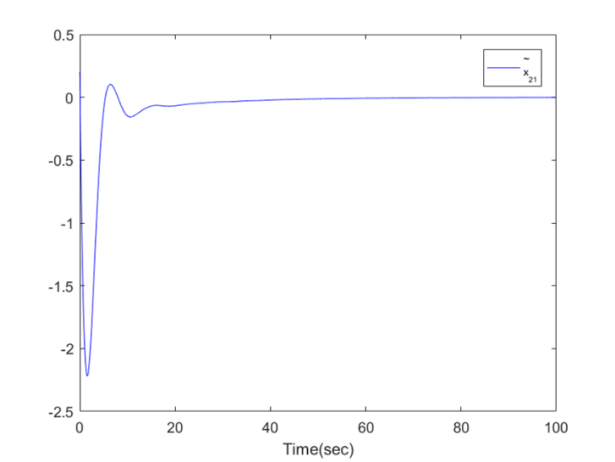 | Figure 9. The trajectory of  for Example 1 for Example 1 |
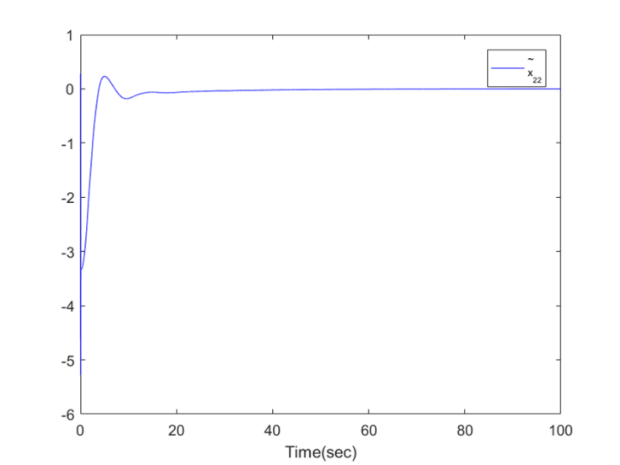 | Figure 10. The trajectory of  for Example1 for Example1 |
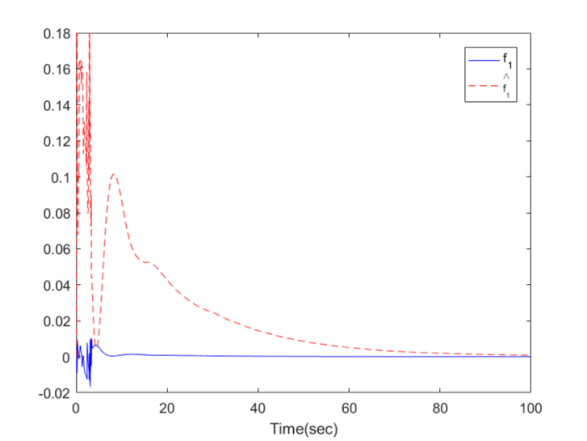 | Figure 11. The trajectories of  and and  for Example 1 for Example 1 |
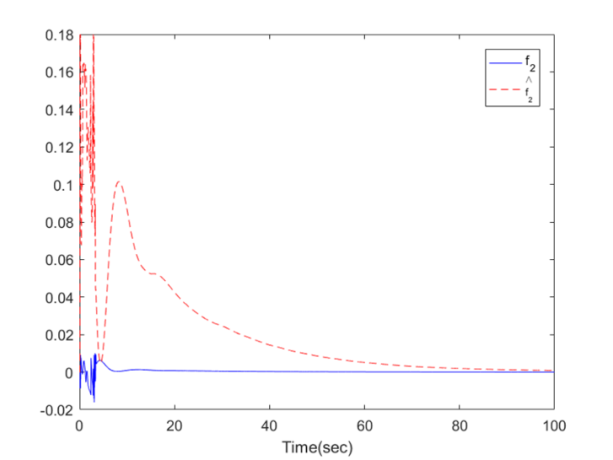 | Figure 12. The trajectories of 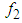 and and 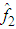 for Example 1 for Example 1 |
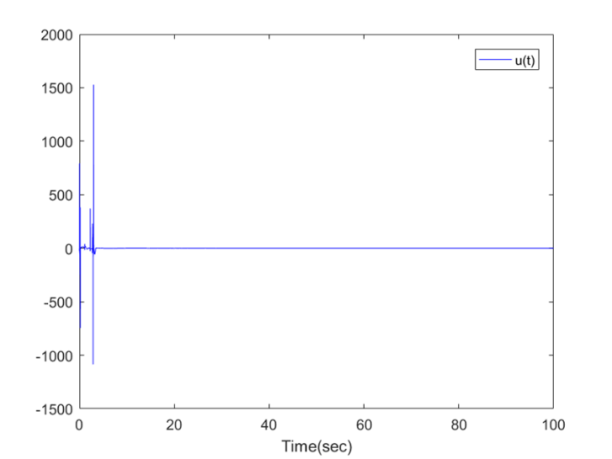 | Figure 13. The control signal 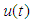 for Example 1 for Example 1 |
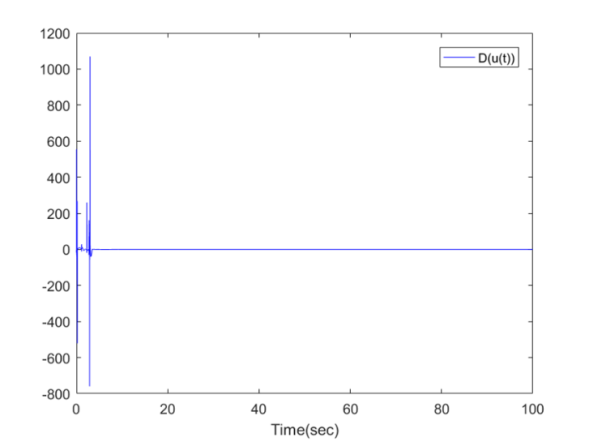 | Figure 14. The dead-zone input 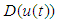 for Example 1 for Example 1 |
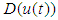 is an output of a dead zone, and
is an output of a dead zone, and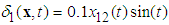 ,
, 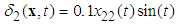 are the disturbances.In the simulation, parameters of the dead zone are
are the disturbances.In the simulation, parameters of the dead zone are 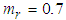 ,
, 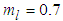 ,
, 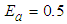 ,
, 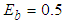 . We select their bounds as
. We select their bounds as 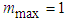 ,
, 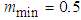 . Six fuzzy sets are defined over the interval [-3, 3] for
. Six fuzzy sets are defined over the interval [-3, 3] for 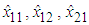 , and
, and 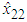 , with labels NB, NM, NS, PS, PM, and PB, and their membership functions are
, with labels NB, NM, NS, PS, PM, and PB, and their membership functions are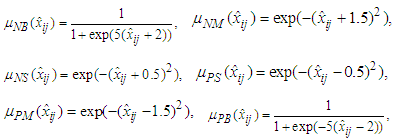 where
where 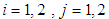 Choose the sampling time as 0.01, and the observer gain as
Choose the sampling time as 0.01, and the observer gain as 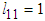 ,
, 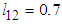 ,
, 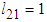 ,
, 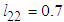 . The initial values are chosen as
. The initial values are chosen as 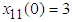 ,
, 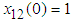 ,
, 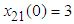 ,
, 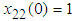 ,
, 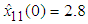 ,
, 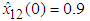 ,
, 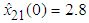 ,
, 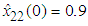 ,
, 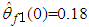 ,
, 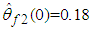 ,
, 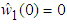 ,
, 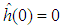 ,
, 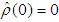 ,
, 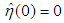 ,
, 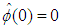 . The other parameters are selected as
. The other parameters are selected as 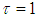 ,
, 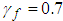 ,
,  ,
, 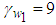 ,
, 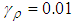 ,
, 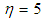 . The simulation results are displayed by Figs. 3-14. Figs. 3-6 show the trajectories of the system states and their estimation states. Figs. 7-10 show the trajectories of the system state estimation errors. Figs. 11-12 show the trajectories of the system functions. Figs. 13-14 show the trajectories of the control signal u and the dead-zone input
. The simulation results are displayed by Figs. 3-14. Figs. 3-6 show the trajectories of the system states and their estimation states. Figs. 7-10 show the trajectories of the system state estimation errors. Figs. 11-12 show the trajectories of the system functions. Figs. 13-14 show the trajectories of the control signal u and the dead-zone input 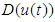 .
.5. Conclusions
- An observer-based robust adaptive fuzzy control approach has been proposed in this paper for a class of uncertain underactuated systems in the presence of time delay and dead-zone input. The system states are assumed to be unmeasurable in this paper. With the help of fuzzy approximation, the fuzzy state observer has been constructed to estimate the unmeasurable states. Additionally, some adaptive laws are employed to estimate the unknown system parameters. The main contribution of this paper can be listed as follows: (i) the stability of the whole underactuated time-delay system has been proved via the Lyapunov-Krasovskii functional and (ii) all the signals of the closed-loop system are bounded by the presented control scheme. Finally, a series of simulation results have been presented to demonstrate the effectiveness of the proposed control approach.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML