-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2019; 9(2): 37-44
doi:10.5923/j.control.20190902.02

Application of Method of Adjustable Model for Identification of Linear Object with Uncertain Parameters and Disturbance
Bukhar Kussainov
Institute of Control Systems and Information Technologies, Almaty University of Power Engineering and Telecommunications, Almaty, Republic of Kazakhstan
Correspondence to: Bukhar Kussainov, Institute of Control Systems and Information Technologies, Almaty University of Power Engineering and Telecommunications, Almaty, Republic of Kazakhstan.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In a wide variety of parametric uncertainties and external disturbance estimation and attenuation methods uncertainties and disturbance are lumped together and an observation algorithm is employed to estimate the total disturbance. While in certain cases of application can be required the separate estimation or identification of uncertain parameters itself and a disturbance. In the paper the separate and simultaneous identification (estimation) of unknown and/or changing parameters and an external disturbance of a linear object is considered. For this porpose the known procedure of synthesis of adaptive observer for estimation of parameters and state coordinates of a n-th order linear object is used taking into account the influence of the scalar external disturbance operating on this object. Developed adaptive observer provides asymptotic stability of processes of separate and simultaneous identification of uncertain parameters and an external disturbance of a n-th order linear object. Asymptotic stability of proposed observer is proved by Lyapunov’s direct method. As an example of using of the offered adaptive observer the structure and algorithm of joint identification of the moment of inertia (parameter) and the torque of resistance (external disturbance) of mechanical load of dc electric drive model are obtained. Asymptotic stability of processes of joint identification of the parameter and external disturbance of drive model is proved. Simulation results of identification processes and their using for control system adaptation are shown on graphs of transition processes. Designed algorithm for the joint identification of parameter and external disturbance of plant provide adaptive stabilization of desirable dynamic properties of control system with adaptive observer.
Keywords: Uncertainties and disturbance, Estimation algorithm, Adaptive observer, Adaptive control system
Cite this paper: Bukhar Kussainov, Application of Method of Adjustable Model for Identification of Linear Object with Uncertain Parameters and Disturbance, International Journal of Control Science and Engineering, Vol. 9 No. 2, 2019, pp. 37-44. doi: 10.5923/j.control.20190902.02.
Article Outline
1. Introduction
- Difficult dynamical controlled systems (aircrafts, mechatronic systems, technological processes, etc.) in the course of work are characterized by uncertain (unknown) and/or changing parameters (coefficients of the differential equations) and an external disturbance action. Parametric uncertainties and a disturbance can cause a deterioration of performance quality and lead even to an instability of control system. To keep the desired control quality of such plants it is necessary to reject an external disturbance and suppress uncertainties of parameters. The solving of this problem is carried out due to estimation (observation, identification) of uncertain parameters and an external disturbance and then using their estimates for the adaptation of control system to perturbations of parameters and a disturbance. In modern control engineering there is a wide variety of parametric uncertainties and external disturbance estimation and attenuation methods/techniques and many research publications in this area based on the following most popular of them: time delay control (TDC) [1], uncertainty and disturbance estimator (UDE) [2], extended state observer (ESO) [3], equivalent input disturbance (EID) [4], disturbance observer (DOB) [5], active disturbance rejection control (ADRC) [6]. According to [7] in all of these methods, uncertainties and disturbance are lumped together, and an observation algorithm is employed to estimate the total disturbance. The uncertainties and disturbance estimation is integrated and it is only then performed if there is a disturbance or/and there are deviations/perturbations of parameters from their nominal values. Therefore, abovementioned methods/techniques cannot estimate each of parameters and a disturbance itself, while in certain cases of application can be required the separate and simultaneous estimation of uncertain parameters itself and a disturbance. In this paper for separate estimation of parameters we’ll use the method of generalized adjustable model [8,9] in which the closed contours of estimation of parameters of a n-th order linear object are self-adjustable (adaptive) by the identified parameters. Therefore, the adjustable model is called the adaptive observer in [9] and the adaptive observing device for identification of parameters in [10], besides, the procedure of creation of adaptive observer for a n-th order linear object and the proof of stability of its work are given in [9-12]. This adaptive observer allows also the estimation of unknown state coordinates of a n-th order linear object necessary for implementation of control laws.In this paper the model of a n-th order linear object with unknown parameters is in addition considered with an unknown external disturbance. It is offered for the known adaptive observer to add the identification contour of external disturbance, it is proofed the stability of adaptive observer for separate and simultaneous identification of unknown parameters and disturbance as well as it is considered the application of offered adaptive observer for the first order linear object with an external disturbance.This paper is structured as follows. In Sections 2 and 3 for the adaptive observer of identification of parameters and a disturbance of linear object the structure is developed and the stability is proved, respectively. In Sections 4 and 5 for a linear model of dc electric drive with a variable load the adaptive observer identifying a parameter and a disturbance is designed and its stability is proved, respectively. In Section 6 the simulation results of a control system with the adaptive observer estimating a parameter and a disturbance of dc electric drive are showed. Finally, in Section 7 the main conclusions of this paper are given.
2. The Structure of Adaptive Observer for Identification of Parameters and Disturbance of Linear Object
- Let the linear control object (plant) has: 1) the known n-th order linear structure in which
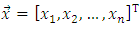 is the vector of state coordinates; 2) the known scalar input
is the vector of state coordinates; 2) the known scalar input 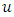 and output
and output 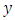 signals and
signals and 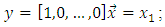 3) unknown parameters; 4) an unknown scalar external disturbance
3) unknown parameters; 4) an unknown scalar external disturbance 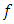 ; 5) the unknown
; 5) the unknown 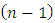 – dimensional vector of state coordinates
– dimensional vector of state coordinates 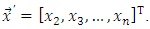 The considered plant we’ll describe by means of the following equation:
The considered plant we’ll describe by means of the following equation: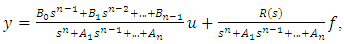 | (1) |
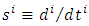 ,
, 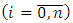 is the differentiation operator;
is the differentiation operator; 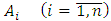 ,
, 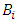 ,
, 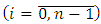 are the unknown coefficients (parameters) of plant;
are the unknown coefficients (parameters) of plant; 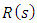 is the polynom depending from a place of action of an external disturbance f.Let’s assume that
is the polynom depending from a place of action of an external disturbance f.Let’s assume that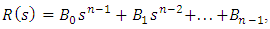 i.e. the unknown scalar external disturbance f also operates at the input of plant as the known scalar input signal u.According to the technique stated in [10, 11] for identification of parameters
i.e. the unknown scalar external disturbance f also operates at the input of plant as the known scalar input signal u.According to the technique stated in [10, 11] for identification of parameters 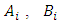 we’ll divide the numerator and the denominator of transfer function (1) of plant by the
we’ll divide the numerator and the denominator of transfer function (1) of plant by the 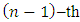 degree polynom which roots are real negative single numbers:
degree polynom which roots are real negative single numbers: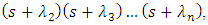 where
where 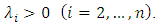 Having decomposed the numerator and the denominator to simple fractions let’s write the Eq. (1) in the following form:
Having decomposed the numerator and the denominator to simple fractions let’s write the Eq. (1) in the following form: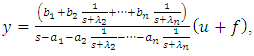 | (2) |
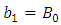 ;
; 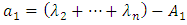 ;
; 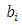 ,
, 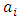
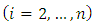 are incorporated with parameters
are incorporated with parameters 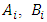 and
and 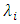 via more difficult relations.Let’s write the Eq. (2) in the following form:
via more difficult relations.Let’s write the Eq. (2) in the following form: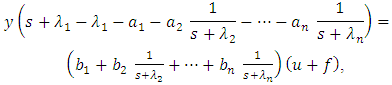 hence
hence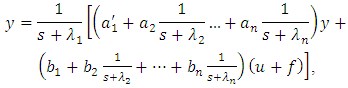 | (3) |
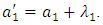 The observer for identification of unknown values
The observer for identification of unknown values 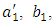
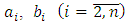 and f is builds on the Eq. (3). Having replaced these values by their estimates
and f is builds on the Eq. (3). Having replaced these values by their estimates 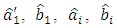
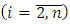 and
and 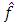 we’ll rewrite the Eq. (3) in the following form:
we’ll rewrite the Eq. (3) in the following form: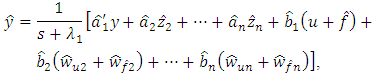 | (4) |
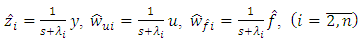 are the intermediate values of observer;
are the intermediate values of observer; 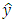 is the estimate of y received at the output of the observer.Let’s form the estimates
is the estimate of y received at the output of the observer.Let’s form the estimates 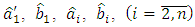 in accordance with the following equations:
in accordance with the following equations: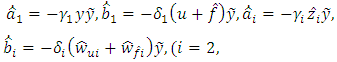 | (5) |
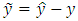 is the difference between estimated in observer and measured in plant values of the output signal;
is the difference between estimated in observer and measured in plant values of the output signal; 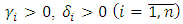 are coefficients of amplification of integrators.Thus, the estimates
are coefficients of amplification of integrators.Thus, the estimates 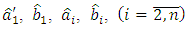 form at the output of integrators with the corresponding coefficients of amplification. The input signals of integrators are the difference between the estimated
form at the output of integrators with the corresponding coefficients of amplification. The input signals of integrators are the difference between the estimated 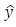 in observer and measured y in plant values of output signal multiplied by corresponding signals
in observer and measured y in plant values of output signal multiplied by corresponding signals 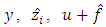 or
or 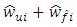 . The estimate of value of external disturbance
. The estimate of value of external disturbance 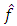 we’ll also receive at the output of integrator with the coefficient of amplification
we’ll also receive at the output of integrator with the coefficient of amplification 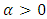 by the following equation:
by the following equation: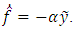 | (6) |
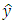 and y signals.Variables
and y signals.Variables 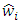 and
and 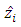 are also used for estimation of unknown state coordinates of plant:
are also used for estimation of unknown state coordinates of plant: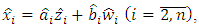 | (7) |
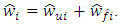 The block diagram of observer for identification of unknown parameters and external disturbance of plant showed in the Fig.1 is completely corresponded to the equations (3) – (6). In this scheme the place of action of the estimation
The block diagram of observer for identification of unknown parameters and external disturbance of plant showed in the Fig.1 is completely corresponded to the equations (3) – (6). In this scheme the place of action of the estimation 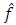 of external disturbance is showed at the input of observer as
of external disturbance is showed at the input of observer as 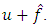 Generally, in Eq. (4) the place of action of the estimation
Generally, in Eq. (4) the place of action of the estimation 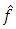 in observer should be defined in accordance with the place of action of the external disturbance f in the block diagram of plant.
in observer should be defined in accordance with the place of action of the external disturbance f in the block diagram of plant.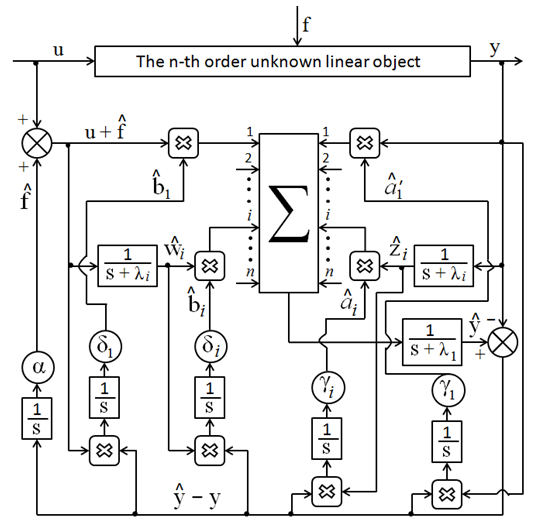 | Figure 1. Block diagram of adaptive observer |
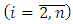 and external disturbance
and external disturbance 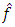 of plant received at the outputs of corresponding integrators as well as the signals
of plant received at the outputs of corresponding integrators as well as the signals 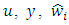 and
and 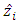 close the structure of observer according to the Eq. (4). These closed contours of observer are self-adjustable on the identified values, i.e. in observer it is performed not only the identification of unknown parameters and external disturbance, but also the adaptation to their changes in process of functioning of plant. Therefore, the considered observer can be called the adaptive observer. At the same time by means of the corresponding choice of amplification coefficients of integrators
close the structure of observer according to the Eq. (4). These closed contours of observer are self-adjustable on the identified values, i.e. in observer it is performed not only the identification of unknown parameters and external disturbance, but also the adaptation to their changes in process of functioning of plant. Therefore, the considered observer can be called the adaptive observer. At the same time by means of the corresponding choice of amplification coefficients of integrators 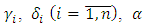 it is performed the optimisation of identification processes in order the estimation transitional processes in observer will be more quicker than transitional process in basic contour of control system.The estimates of parameters
it is performed the optimisation of identification processes in order the estimation transitional processes in observer will be more quicker than transitional process in basic contour of control system.The estimates of parameters 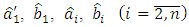 and external disturbance
and external disturbance 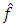 of n-th order linear object being the output signals of corresponding integrators of adaptive observer can be used for formation of algorithms of control of linear objects with uncertain and/or changing parameters
of n-th order linear object being the output signals of corresponding integrators of adaptive observer can be used for formation of algorithms of control of linear objects with uncertain and/or changing parameters 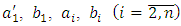 and disturbance f.
and disturbance f.3. The Stability of Adaptive Observer for Identification of Parameters and Disturbance of Linear Object
- Research the stability of plant by means of Lyapunov’s direct method. Let’s write the Eq. (3) for a plant in the following form:
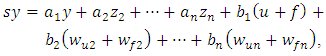 | (8) |
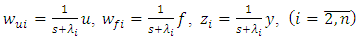 are the intermediate variables of plant.This Eq. (8) it is possible also to obtain if the Eq. (1) of plant is represented in a canonical form as in [10] but with taking into account an external disturbance f:
are the intermediate variables of plant.This Eq. (8) it is possible also to obtain if the Eq. (1) of plant is represented in a canonical form as in [10] but with taking into account an external disturbance f: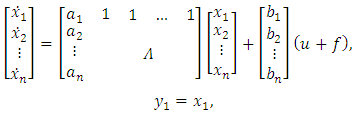 | (9) |
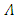 is the
is the 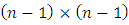 - diagonal matrix, which elements are the numbers
- diagonal matrix, which elements are the numbers 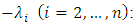
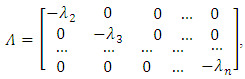
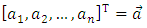 ,
, 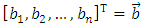 are the parametric vectors.Since a coordinate
are the parametric vectors.Since a coordinate 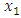 is measured and is equal y, we can write the Eq. (9) of plant in the following form:
is measured and is equal y, we can write the Eq. (9) of plant in the following form: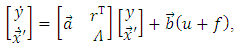 | (10) |
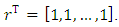 Let’s write the Eq. (4) for observer in the following form:
Let’s write the Eq. (4) for observer in the following form: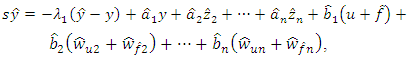 | (11) |
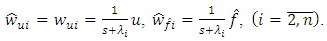 The same Eq. (11) it is possible to obtain if equations of observer are represented in the form as in [9] but with taking into account the estimate of external disturbance
The same Eq. (11) it is possible to obtain if equations of observer are represented in the form as in [9] but with taking into account the estimate of external disturbance 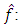
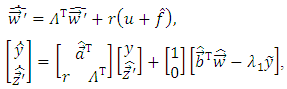 | (12) |
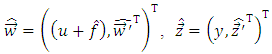 and
and 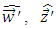 are
are 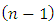 – vectors of intermediate variables
– vectors of intermediate variables 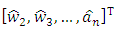
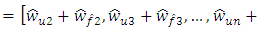
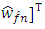 and
and 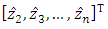 of observer.Let’s enter designations:
of observer.Let’s enter designations: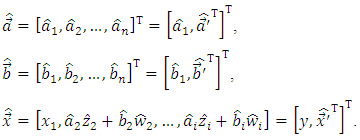 Let’s represent the Eq. (10) of plant in such form as the equation (12) of observer:
Let’s represent the Eq. (10) of plant in such form as the equation (12) of observer: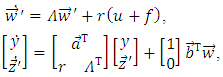 | (13) |
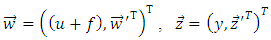 and
and 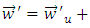
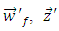 are
are 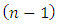 – vectors of intermediate variables
– vectors of intermediate variables 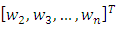
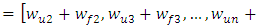
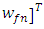 and
and 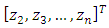 of plant.Subtract the Eq. (8) (or (13)) from the Eq. (11) (or (12)) with taking into account that
of plant.Subtract the Eq. (8) (or (13)) from the Eq. (11) (or (12)) with taking into account that 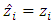 and
and 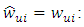
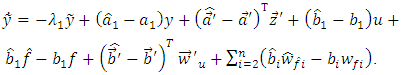 | (14) |
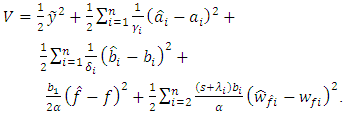 | (15) |
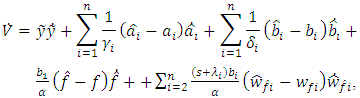 | (16) |
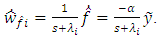 Eq. (16) of a derivative
Eq. (16) of a derivative 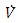 according to the observer equations (5), (6) and the deviation Eq. (14) has the same result as in [10]:
according to the observer equations (5), (6) and the deviation Eq. (14) has the same result as in [10]: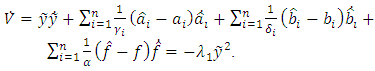 | (17) |
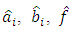 asymptotically converge to their real values
asymptotically converge to their real values 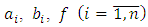 in plant. A speed of convergence depends of coefficients of integrators
in plant. A speed of convergence depends of coefficients of integrators 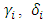 and
and 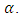 At the same time on the basis of a hypothesis of quasistationarity [11,12] it is supposed that during transition processes in observer variables
At the same time on the basis of a hypothesis of quasistationarity [11,12] it is supposed that during transition processes in observer variables 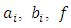
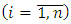 in plant do not change.
in plant do not change.4. Design of Adaptive Observer for Identification of Linear Model of DC Electric Drive with Variable Load
- Consider the application of adaptive observer described by the equations (4) – (6) for a linear object with disturbance. As such linear object could be considered a linear model of the electric drive in mobility degree of the multilink manipulator robot (MR) being the joint drive with a variable mechanical load [13-15].The equation of moments on a shaft of the direct current (dc) electric motor:
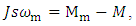 | (18) |
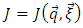 is the moment of inertia of drive load changing in dependence on a vector
is the moment of inertia of drive load changing in dependence on a vector 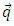 of generalized coordinates and a vector
of generalized coordinates and a vector 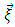 of parameters of MR and its payload (geometrical, weight-inertial parameters, etc.) [16], i.e. is the unknown parameter of plant;
of parameters of MR and its payload (geometrical, weight-inertial parameters, etc.) [16], i.e. is the unknown parameter of plant; 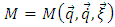 is counted to a shaft of motor the torque of resistance of the drive load which changes are caused by mutual influence of movements on degrees of mobility of MR, moments from the gravity of links and a payload of MR, etc. [16], i.e. is the external disturbing signal for a plant;
is counted to a shaft of motor the torque of resistance of the drive load which changes are caused by mutual influence of movements on degrees of mobility of MR, moments from the gravity of links and a payload of MR, etc. [16], i.e. is the external disturbing signal for a plant; 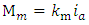 is the torque of dc motor in which
is the torque of dc motor in which 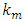 is the motor’s torque constant,
is the motor’s torque constant, 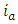 is the armature current being the input signal for a plant;
is the armature current being the input signal for a plant; 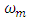 is the speed of rotation of the shaft of motor being the output signal for a plant;
is the speed of rotation of the shaft of motor being the output signal for a plant; 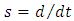 is the differentiation operator.Let’s represent the Eq. (18) of plant in the following form:
is the differentiation operator.Let’s represent the Eq. (18) of plant in the following form: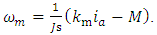 | (19) |
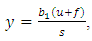 | (20) |
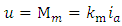 is the input signal of plant measured by means of the armature current sensor with a transfer coefficient
is the input signal of plant measured by means of the armature current sensor with a transfer coefficient 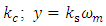 is the output signal of plant measured by means of the speed sensor with a transfer coefficient
is the output signal of plant measured by means of the speed sensor with a transfer coefficient 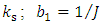 is the unknown parameter of plant;
is the unknown parameter of plant; 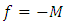 is the unknown external disturbance signal of plant.On the basis of the measured input
is the unknown external disturbance signal of plant.On the basis of the measured input 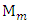 and output
and output 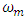 signals of plant (18)-(20) and according to the basic provisions of design of observer stated above it is necessary to estimate the unknown values of parameter
signals of plant (18)-(20) and according to the basic provisions of design of observer stated above it is necessary to estimate the unknown values of parameter 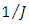 and external disturbance M of the considered plant.Since the Eq. (20) has the 1st order the equation for 1st order observer obtained on the Eq. (4) at
and external disturbance M of the considered plant.Since the Eq. (20) has the 1st order the equation for 1st order observer obtained on the Eq. (4) at 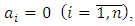
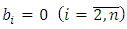 has the following form:
has the following form: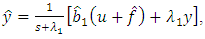 | (21) |
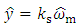 is the estimate of output signal
is the estimate of output signal  equal to the estimate of angular velocity of the shaft of motor
equal to the estimate of angular velocity of the shaft of motor 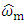 with a transfer coefficient
with a transfer coefficient 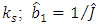 is the estimate of unknown parameter
is the estimate of unknown parameter 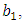 in which
in which 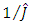 is the inverse value of the estimate
is the inverse value of the estimate 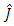 of unknown moment of inertia of drive load;
of unknown moment of inertia of drive load; 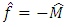 is the estimate of the external disturbance being the estimate of the torque of resistance of drive load.Estimates of the parameter
is the estimate of the external disturbance being the estimate of the torque of resistance of drive load.Estimates of the parameter 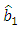 and disturbance
and disturbance 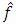 are formed at the outputs of corresponding integrators according to equations (5), (6) by the following formulas:
are formed at the outputs of corresponding integrators according to equations (5), (6) by the following formulas: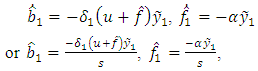 | (22) |
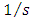 is the integration operator.The block diagram of observer for the considered 1st order plant corresponding to the equations (21), (22) is showed in the Fig. 2,a. Let’s transform this scheme to the form showed in the Fig. 2,b conforming more to the model of plant (19).
is the integration operator.The block diagram of observer for the considered 1st order plant corresponding to the equations (21), (22) is showed in the Fig. 2,a. Let’s transform this scheme to the form showed in the Fig. 2,b conforming more to the model of plant (19).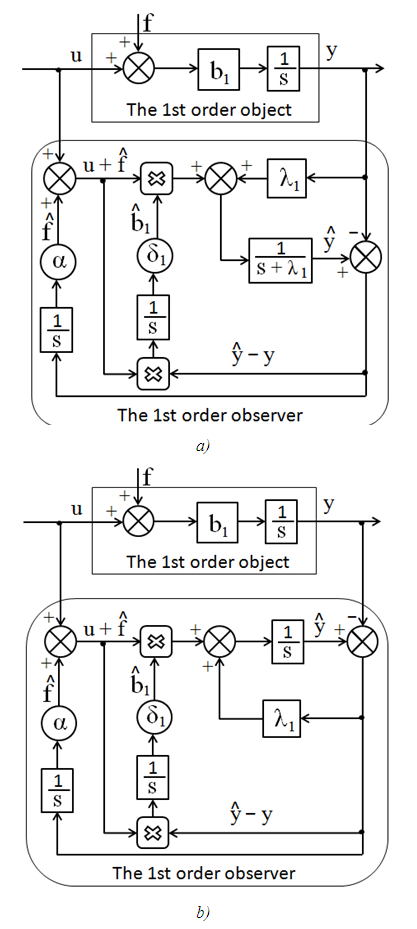 | Figure 2. Block diagrams of observer for the 1st order object |
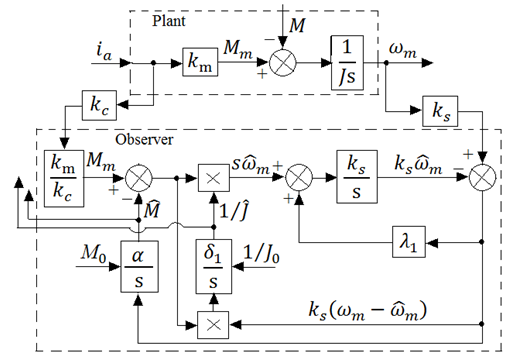 | Figure 3. Block diagrams of 1st order plant and its observer |
5. The Stability of Adaptive Observer for Identification of Parameter and Disturbance of Electric Drive
- For obtaining the estimate
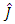 of moment of inertia J and the estimate
of moment of inertia J and the estimate 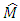 of torque of resistance M of mechanical load of electric drive the algorithm of operating of adaptive observer according to the block diagram in the Fig. 3 has the following form [17]:
of torque of resistance M of mechanical load of electric drive the algorithm of operating of adaptive observer according to the block diagram in the Fig. 3 has the following form [17]: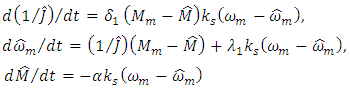 | (23) |
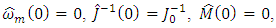 where
where 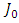 is the average value from the possible range of changes of moment of inertia J.Consider the stability of the adaptive observer for identification of
is the average value from the possible range of changes of moment of inertia J.Consider the stability of the adaptive observer for identification of 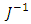 and
and 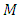 variables. Let’s use the following designations:
variables. Let’s use the following designations: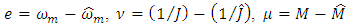 and take into account that
and take into account that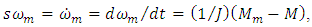 then the operation algorithm of the adaptive observer in
then the operation algorithm of the adaptive observer in 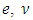 and
and 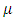 coordinates can be described by the equations:
coordinates can be described by the equations: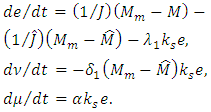 | (24) |
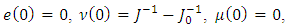 and on the basis of a hypothesis of quasistationarity [11,12] we’ll consider that on the time interval corresponding to transition process in observer the variables
and on the basis of a hypothesis of quasistationarity [11,12] we’ll consider that on the time interval corresponding to transition process in observer the variables 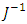 and
and 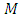 do not change.Let’s prove that the position of balance of system of the equations (24) is asymptotically stable, i.e.
do not change.Let’s prove that the position of balance of system of the equations (24) is asymptotically stable, i.e.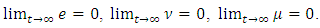 Let’s consider a positive-definite Lyapunov’s function of a following form:
Let’s consider a positive-definite Lyapunov’s function of a following form: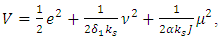 | (25) |
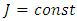 - because it corresponds to a quasistationarity interval.Considering that
- because it corresponds to a quasistationarity interval.Considering that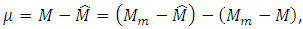 Let's write down a full derivative of Eq. (25) with respect to time on the basis of system of the equations (24):
Let's write down a full derivative of Eq. (25) with respect to time on the basis of system of the equations (24):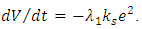 | (26) |
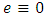 there are also
there are also 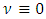 and
and 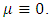 For this purpose we will consider at
For this purpose we will consider at 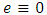 the system of equations (24):
the system of equations (24):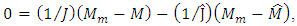
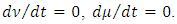 The equality to zero of the first equation means
The equality to zero of the first equation means 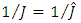 and
and 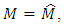 therefore at
therefore at 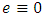 the identical equality to zero of
the identical equality to zero of 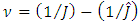 and
and 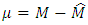 parameters are obviously. Therefore, the function
parameters are obviously. Therefore, the function 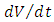 is negative-definite and if the identification observer would be constructed according to equations (23) the
is negative-definite and if the identification observer would be constructed according to equations (23) the 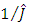 and
and 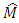 estimates would asymptotically approach to their actual values of the moment of inertia
estimates would asymptotically approach to their actual values of the moment of inertia 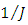 and the torque of resistance M of load of the drive. The convergence of process of estimate depends on
and the torque of resistance M of load of the drive. The convergence of process of estimate depends on 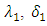 and
and 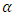 coefficients, which can be practically always chosen from a condition that the estimation processes in adaptive observer be occurred quicker than the main transition process in control system of the drive.
coefficients, which can be practically always chosen from a condition that the estimation processes in adaptive observer be occurred quicker than the main transition process in control system of the drive.6. Simulation Results of Control System with Adaptive Observer for Identification of Parameter and Disturbance
- In addition to the Eq. (16) of plant let’s write the following equations for forming of control signal [15,18]:
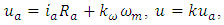 | (27) |
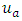 and
and 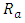 are the armature voltage and the armature resistance of electric motor;
are the armature voltage and the armature resistance of electric motor; 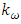 is the motor’s back-emf constant;
is the motor’s back-emf constant; 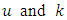 are the control signal and the amplification coefficient of power amplifier of drive.Taking into account the equations (27) it is possible to write the Eq. (19) of plant in following form:
are the control signal and the amplification coefficient of power amplifier of drive.Taking into account the equations (27) it is possible to write the Eq. (19) of plant in following form: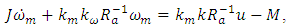 | (28) |
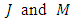 are the unknown variables.Let the control signal of drive has the following form [19,20]:
are the unknown variables.Let the control signal of drive has the following form [19,20]: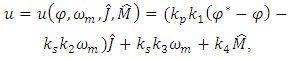 | (29) |
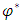 and
and 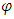 are respectively the demand and the actual angular positions of an output shaft of the drive;
are respectively the demand and the actual angular positions of an output shaft of the drive; 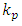 is the transfer coefficient of sensor of angular position of a shaft of the drive;
is the transfer coefficient of sensor of angular position of a shaft of the drive; 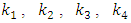 are the constant parameters selected so, that at
are the constant parameters selected so, that at 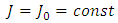 and
and 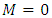 set in model of the drive (28), the desirable transition process of control system at
set in model of the drive (28), the desirable transition process of control system at 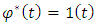 will have the set duration
will have the set duration 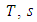 and the set overshoot
and the set overshoot 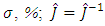 and
and 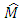 are the estimates received in observer on the equations (23).In the program of simulation the different values of the moment of inertia
are the estimates received in observer on the equations (23).In the program of simulation the different values of the moment of inertia 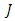 and the external torque
and the external torque 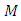 of load are set in the Eq. (28), these given values of load are estimated in observer on an algorithm (23) and used for formation of a control algorithm (29) [19, 20]. Results of simulation of dynamics of control of a rotation link drive of MR at variable values of mechanical load are given in Figures 4, 5 and 6.
of load are set in the Eq. (28), these given values of load are estimated in observer on an algorithm (23) and used for formation of a control algorithm (29) [19, 20]. Results of simulation of dynamics of control of a rotation link drive of MR at variable values of mechanical load are given in Figures 4, 5 and 6. 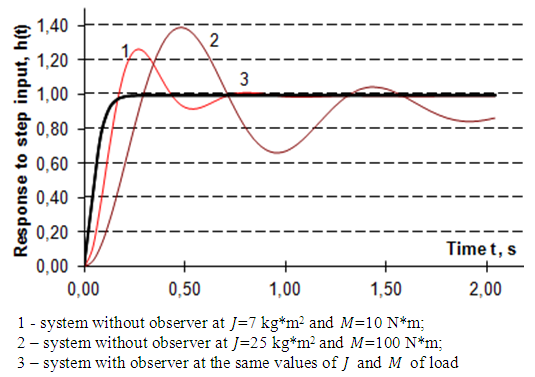 | Figure 4. The graphs of 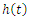 transition functions transition functions |
 | Figure 5. Transition processes of identification of the moment of inertia of load |
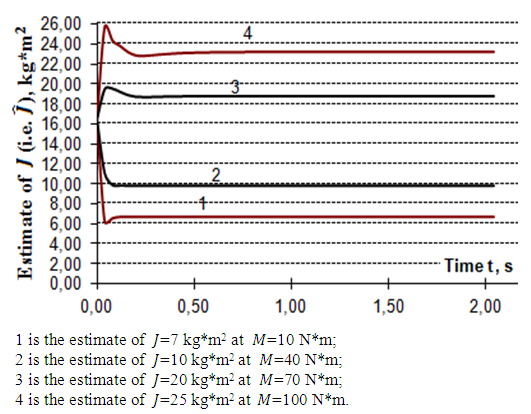
 | Figure 6. Transition processes of identification of the external torque of load |
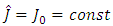 and
and 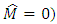 it is possible to see that to increase in the values of J and M there is a deterioration in characteristics of transitional functions
it is possible to see that to increase in the values of J and M there is a deterioration in characteristics of transitional functions 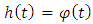 (duration, overshoot and steady-state error increase) - in the Fig. 4, the curves 1 and 2. While in control system with observer at these different values of mechanical load the characteristics of transitional functions don't change (the Fig. 4, a curve 3), i.e. independent of changes of load in control system with observer the set duration and overshoot of desired transition process always take place, and the steady-state error of the control system is completely eliminated.The graphs in Figures 4, 5, 6 of transition processes in observer at the identification of different values of the moment of inertia J and the external torque M of load set in model of the drive (28) have shown that the use of the values J and M estimated in observer to form an adaptive control algorithm (29) provides the invariable characteristics of transitional functions in the control system, i.e. independent of changes of mechanical drive load in control system with observer the desirable transition process - a curve 3 in the Fig. 4 always takes place.In the Figures 5, 6 are shown curves 1 - 4 of transition processes in observer at the identification of unknown values of the moments of inertia J and the external torques of load M set in the drive model (28). From curves in Figures 4, 5 and 6 it is also visible that process of estimation of unknown variables of the moments of inertia J happens quicker than transition process in the main contour of control system, that is necessary for the stable work of a load adaptive control system of the drive, and the estimated values of the unknown external torques M of load eliminate a steady-state error of the drive.
(duration, overshoot and steady-state error increase) - in the Fig. 4, the curves 1 and 2. While in control system with observer at these different values of mechanical load the characteristics of transitional functions don't change (the Fig. 4, a curve 3), i.e. independent of changes of load in control system with observer the set duration and overshoot of desired transition process always take place, and the steady-state error of the control system is completely eliminated.The graphs in Figures 4, 5, 6 of transition processes in observer at the identification of different values of the moment of inertia J and the external torque M of load set in model of the drive (28) have shown that the use of the values J and M estimated in observer to form an adaptive control algorithm (29) provides the invariable characteristics of transitional functions in the control system, i.e. independent of changes of mechanical drive load in control system with observer the desirable transition process - a curve 3 in the Fig. 4 always takes place.In the Figures 5, 6 are shown curves 1 - 4 of transition processes in observer at the identification of unknown values of the moments of inertia J and the external torques of load M set in the drive model (28). From curves in Figures 4, 5 and 6 it is also visible that process of estimation of unknown variables of the moments of inertia J happens quicker than transition process in the main contour of control system, that is necessary for the stable work of a load adaptive control system of the drive, and the estimated values of the unknown external torques M of load eliminate a steady-state error of the drive.7. Conclusions
- In the paper the known procedure of synthesis of adaptive observer for identification of parameters and state coordinates of linear object is considered taking into account the identification of the scalar external disturbance operating on control object. In the block diagram of adaptive observer the place of action of the estimation
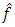 of external disturbance is showed at the input of observer and the obtained observer provides asymptotic stability of processes for identification of parameters and external disturbance of object. Generally, the place of action of the estimation
of external disturbance is showed at the input of observer and the obtained observer provides asymptotic stability of processes for identification of parameters and external disturbance of object. Generally, the place of action of the estimation 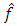 in observer should be defined in accordance with the place of action of the external disturbance f in the block diagram of control object. Using considered in the paper technique it is possible to design the adaptive observer and prove its asymptotic stability of processes for identification of parameters and an external disturbance for other physical linear control objects (plants).An example of use of the proposed adaptive observer for linear model of the dc electric drive with the variable mechanical load is showed that the processes for identification of the moment of inertia and the torque of resistance of drive load, i.e. the processes for identification of the uncertain parameter and an external disturbance of linear object are carried out simultaneously (concurrently, joint). Asymptotic stability of identification processes of uncertain parameter and external disturbance is proved. Received results of identification and their use for adaptation of an example of linear object are shown on graphs of transition processes and provide adaptive stabilization of desirable dynamic properties of considered control system.
in observer should be defined in accordance with the place of action of the external disturbance f in the block diagram of control object. Using considered in the paper technique it is possible to design the adaptive observer and prove its asymptotic stability of processes for identification of parameters and an external disturbance for other physical linear control objects (plants).An example of use of the proposed adaptive observer for linear model of the dc electric drive with the variable mechanical load is showed that the processes for identification of the moment of inertia and the torque of resistance of drive load, i.e. the processes for identification of the uncertain parameter and an external disturbance of linear object are carried out simultaneously (concurrently, joint). Asymptotic stability of identification processes of uncertain parameter and external disturbance is proved. Received results of identification and their use for adaptation of an example of linear object are shown on graphs of transition processes and provide adaptive stabilization of desirable dynamic properties of considered control system.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML