-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2019; 9(2): 27-36
doi:10.5923/j.control.20190902.01

Observer-Based Adaptive Fuzzy Sliding Mode Control for Switched Uncertain Nonlinear Systems with Dead-Zone Input
Chiang-Cheng Chiang, Chin-Cheng Kuo
Department of Electrical Engineering, Tatung University, Taipei, Taiwan, Republic of China
Correspondence to: Chiang-Cheng Chiang, Department of Electrical Engineering, Tatung University, Taipei, Taiwan, Republic of China.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper considers the problem of observer-based adaptive fuzzy sliding mode control for switched uncertain nonlinear systems with dead-zone input in strict-feedback form. The explored switched systems include unknown nonlinearities, dead-zone and immeasurable states. Fuzzy logic systems are used to approximate unknown nonlinear functions of the dynamic system and unknown upper bounds of uncertainties, respectively. A state observer based on state variable filters is developed to estimate the immeasurable states. Adaptive technique and sliding mode control method are utilized to construct a controller. By choosing an appropriate Lyapunov function, the proposed controller is designed to demonstrate that all the signals in the closed-loop system can not only guarantee uniformly ultimately bounded, but also achieve good tracking performance. Finally, the simulation results are provided to demonstrate the effectiveness of the proposed approach.
Keywords: Switched system, Strict-feedback form, Lyapunov function, Sliding mode control, Dead-zone, Fuzzy logic system
Cite this paper: Chiang-Cheng Chiang, Chin-Cheng Kuo, Observer-Based Adaptive Fuzzy Sliding Mode Control for Switched Uncertain Nonlinear Systems with Dead-Zone Input, International Journal of Control Science and Engineering, Vol. 9 No. 2, 2019, pp. 27-36. doi: 10.5923/j.control.20190902.01.
Article Outline
1. Introduction
- In recent years, switched systems have drawn much attention and some significant results have been obtained in the literature. As an important class of hybrid systems, switched systems can be described by a family of subsystems and a switching law between them. Actually, many practical systems, such as power electronic, automotive industry, mechanical systems, air traffic control, etc., can be expressed as switched systems [1-4]. Motivated by the above reasons, the control design and stability of the switched systems have received many researchers a great interest. In addition, dead-zone input nonlinearity is a nonsmooth function that features certain insensitivity for small control inputs which is often encountered in a variety of practical systems such as the single-link flexible joint manipulator, and so on [5, 17-18]. In this paper, the switched system in strict-feedback form is investigated and a feasible and systematic methodology is proposed to solve the tracking control problem.Due to uncertainties inherent in practical systems, the design control capable of handling uncertainties is of practical interest and is challenging. To achieve the desired system performance, adaptive control is a valid methodology, which supplies adaptation mechanisms to regulate controllers for systems with some uncertainties, such as parametric, structural, and environmental uncertainties [6-7]. For non-switched nonlinear systems using fuzzy logic systems or neural networks to parameterise the unknown non-linearities, adaptive control of uncertain nonlinear systems has attracted much attention [8-9]. In recent years, adaptive fuzzy or neural backstepping approaches for strict-feedback form systems [10-11] provide some systematic methods to achieve good tracking performance.Fuzzy logic systems (FLS) with appropriate adaptive laws algorithms are used to approximate the unknown nonlinear functions appearing in the structure of the switched system. A FLS consists of four parts: the knowledge base, the fuzzifier, the fuzzy inference engine working on fuzzy rules, and the defuzzifier. The problem of adaptive fuzzy output-feedback control for switched uncertain non-linear systems is investigated in [12, 19]. In [13], Li et al. introduced an adaptive fuzzy output-feedback stabilization controller to treat the problem for a class of switched nonstrict-feedback nonlinear systems.Recently, sliding mode control (SMC) has been adopted as a powerful approach for the control of systems with external disturbances and parameter variations [14, 20]. Since SMC technique has some advantages, such as insensitivity to system parameter variations, invariance to external disturbances, good transient and fast response. Basically, SMC laws consist of two parts: switching controller design and equivalent controller design. The switching control law is employed to lead the system’s states to a given sliding surface and the equivalent control law guarantees the system’s states to stay on the aforementioned sliding surface and converge to zero along the sliding surface.The main contribution of this paper is that the proposed SMC method deals with the problem of tracking performance and stability for a class of switched nonlinear systems in strict-feedback form with dead-zone input. Based on SMC technique, an adaptive fuzzy sliding mode controller is designed for the switched system by using fuzzy logic systems with some adaptive laws to approximate uncertain functions. The fuzzy state observer is employed to estimate the unavailable state for measurement. By choosing an appropriate Lyapunov function, it is theoretically ensured that all the signals in the closed-loop system are uniformly ultimately bounded and receive good tracking performance under our designed controller.This paper organized as follows. Section II contains system description, dead-zone characterization, a detailed description systems, and fuzzy basis functions. Section III, the observer-based fuzzy sliding mode controller is utilized to treat the nonlinear switched system with dead-zone input. Simulation results are provided in Section IV to demonstrate the advantages and effectiveness of the proposed approaches Finally, the concluding remarks are gathered in Section V.
2. Problem Statement and Preliminaries
2.1. System Description
- Consider a class of single-input-single-output switched uncertain nonlinear systems in strict-feedback form with dead-zone input expressed as follows:
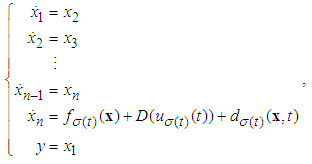 | (1) |
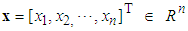 is the system state vector which is assumed to be available for measurement,
is the system state vector which is assumed to be available for measurement,  and
and 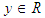 are the input and output of the system output, respectively. The function
are the input and output of the system output, respectively. The function 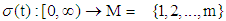 , is a switching signal which is assumed to be a piecewise continuous (from the right) function of time. If
, is a switching signal which is assumed to be a piecewise continuous (from the right) function of time. If 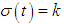 , then we say the kth switched subsystem is active and the remaining switched subsystems are inactive.
, then we say the kth switched subsystem is active and the remaining switched subsystems are inactive. 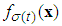 is the unknown smooth nonlinear function,
is the unknown smooth nonlinear function, 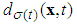 is unknown external bound disturbance.
is unknown external bound disturbance. 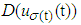 denotes the input function containing a dead-zone.Then, the system (1) can be rewritten as
denotes the input function containing a dead-zone.Then, the system (1) can be rewritten as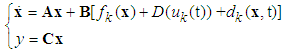 | (2) |
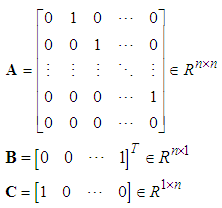
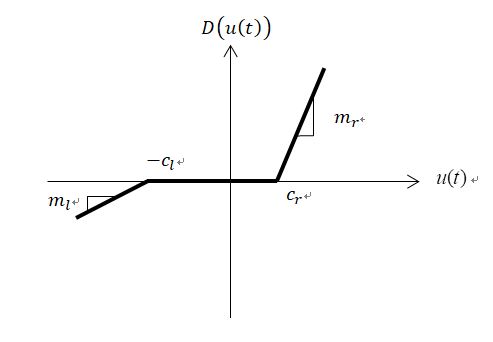 | Figure 1. Dead-zone model |
 and output as shown in the above Fig. 1 is described by
and output as shown in the above Fig. 1 is described by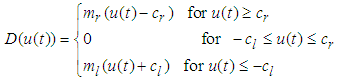 | (3) |
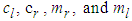 are parameters and slopes of the dead-zone, respectively. In order to investigate the key features of the dead-zone in the control problems, the following assumptions should be made:Assumption 1: The dead-zone output
are parameters and slopes of the dead-zone, respectively. In order to investigate the key features of the dead-zone in the control problems, the following assumptions should be made:Assumption 1: The dead-zone output 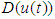 is not available to obtain.Assumption 2: The coefficients
is not available to obtain.Assumption 2: The coefficients 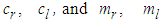 are unknown.Assumption 3: The maximum and minimum values of the characteristic slopes are known.
are unknown.Assumption 3: The maximum and minimum values of the characteristic slopes are known. 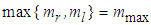 ,
, 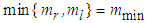 Based on the above assumptions the expression (3) can be represented as
Based on the above assumptions the expression (3) can be represented as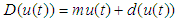 | (4) |
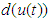 can be calculated form (3) and (4) as
can be calculated form (3) and (4) as 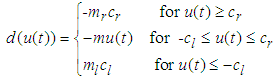 | (5) |
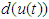 is bounded, and satisfies:
is bounded, and satisfies: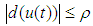 | (6) |
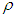 is an upper bound, which can be chosen as
is an upper bound, which can be chosen as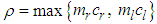 | (7) |
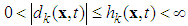 where
where 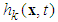 is an unknown function.Control objective: Design a controller for (1) such that the system output y(t) would track the desired output vector
is an unknown function.Control objective: Design a controller for (1) such that the system output y(t) would track the desired output vector 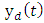 , where
, where 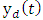 be a given bounded desired signal and contain finite derivative up to the n order. Define the vector of the output tracking error as
be a given bounded desired signal and contain finite derivative up to the n order. Define the vector of the output tracking error as 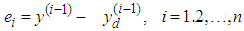 . Thus,
. Thus,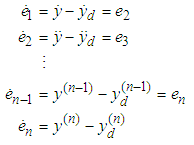 | (8) |
2.2. Description of Fuzzy Logic Systems
- The fuzzy logic system performs a mapping from
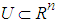 to
to 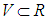 . Let
. Let 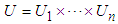 where
where 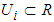 ,
, 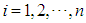 . The fuzzy rule base consists of a collection of fuzzy IF-THEN rules:
. The fuzzy rule base consists of a collection of fuzzy IF-THEN rules: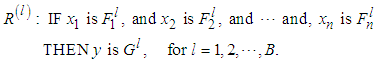 | (9) |
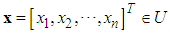 and
and 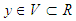 are the input and output of the fuzzy logic system,
are the input and output of the fuzzy logic system, 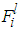 and
and 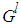 are fuzzy sets in
are fuzzy sets in 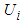 and
and 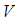 , respectively. The fuzzifier maps a crisp point
, respectively. The fuzzifier maps a crisp point 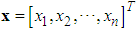 into a fuzzy set in
into a fuzzy set in 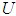 . The fuzzy inference engine performs a mapping from fuzzy sets in
. The fuzzy inference engine performs a mapping from fuzzy sets in 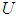 to fuzzy sets in
to fuzzy sets in 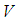 , based upon the fuzzy IF-THEN rules in the fuzzy rule base and the compositional rule of inference. The defuzzifier maps a fuzzy set in
, based upon the fuzzy IF-THEN rules in the fuzzy rule base and the compositional rule of inference. The defuzzifier maps a fuzzy set in 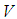 to a crisp point in
to a crisp point in 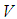 .The fuzzy systems with center-average defuzzifier, product inference and singleton fuzzifier are of the following form:
.The fuzzy systems with center-average defuzzifier, product inference and singleton fuzzifier are of the following form: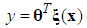 | (10) |
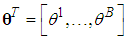 with each variable
with each variable 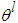 as the point at which the fuzzy membership function of
as the point at which the fuzzy membership function of 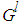 achieves the maximum value and
achieves the maximum value and 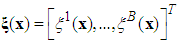 with each variable
with each variable 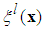 as the fuzzy basis function defined as
as the fuzzy basis function defined as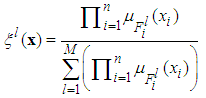 | (11) |
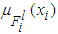 is the membership function of the fuzzy set.
is the membership function of the fuzzy set.3. Controller Design and Stability Analysis
3.1. Observer Design
- According to the description of the fuzzy logic system presented in Section 2.2, we can construct the following fuzzy logic systems, over a compact set, the unknown nonlinear functions
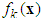 and the uncertainty
and the uncertainty 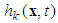 can be approximated as
can be approximated as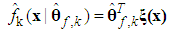 | (12) |
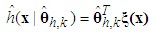 | (13) |
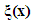 is the fuzzy basic vector,
is the fuzzy basic vector, 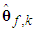 and
and 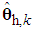 are the corresponding adjustable parameter vectors of each fuzzy logic systems.Owing to the unavailable states of the system and the unavailable elements of the output error vector in many practical systems, the fuzzy logic systems (12) and (13) are not used to control nonlinear systems whose states are not obtained for measurement. Therefore, we must employ an observer to estimate. Let
are the corresponding adjustable parameter vectors of each fuzzy logic systems.Owing to the unavailable states of the system and the unavailable elements of the output error vector in many practical systems, the fuzzy logic systems (12) and (13) are not used to control nonlinear systems whose states are not obtained for measurement. Therefore, we must employ an observer to estimate. Let 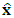 be the estimate of
be the estimate of 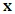 at first. Then, we can obtain the following fuzzy logic systems as
at first. Then, we can obtain the following fuzzy logic systems as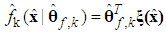 | (14) |
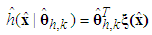 | (15) |
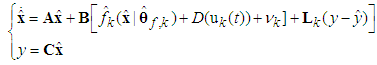 | (16) |
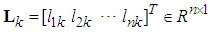 is the observer gain vector, and
is the observer gain vector, and 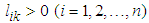 are coefficients of the Hurwitz polynomial
are coefficients of the Hurwitz polynomial 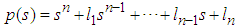 . Define the estimation error vector as
. Define the estimation error vector as 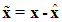 and
and 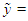
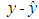 . Then from (2) and (16), we obtain
. Then from (2) and (16), we obtain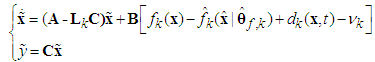 | (17) |
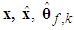 and
and 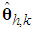 belong to compact sets
belong to compact sets 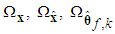 and
and 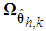 respectively, which is defined as
respectively, which is defined as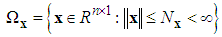 | (18) |
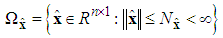 | (19) |
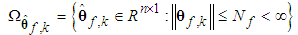 | (20) |
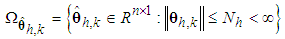 | (21) |
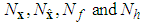 are the designed parameters, and N is the number of fuzzy inference rules. Let us define the optimal parameter vector
are the designed parameters, and N is the number of fuzzy inference rules. Let us define the optimal parameter vector 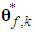 and
and 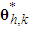 as follows:
as follows: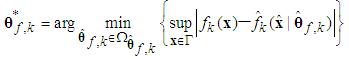 | (22) |
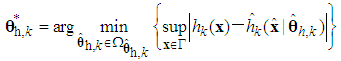 | (23) |
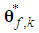 and
and 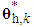 are bounded in the suitable closed set
are bounded in the suitable closed set 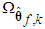 and
and 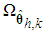 . The parameter estimation errors can be defined as
. The parameter estimation errors can be defined as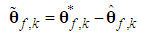 | (24) |
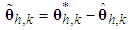 | (25) |
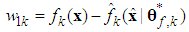 | (26) |
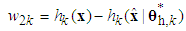 | (27) |
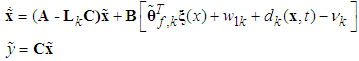 | (28) |
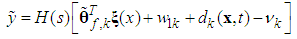 | (29) |
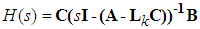 and s denotes the complex Laplace transform variable. As has been discussed, we could not obtain all elements of
and s denotes the complex Laplace transform variable. As has been discussed, we could not obtain all elements of 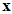 , because not all states of the system are available or measurement. Hence, we could not obtain all elements of
, because not all states of the system are available or measurement. Hence, we could not obtain all elements of 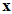 . We will employ the state variable filters [15] to cope with this problem. First, we choose a stable filter
. We will employ the state variable filters [15] to cope with this problem. First, we choose a stable filter 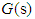 as the following form:
as the following form: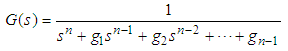 | (30) |
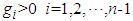 are coefficients of the Hurwitz polynomial
are coefficients of the Hurwitz polynomial 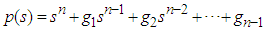 .Introducing (30) into (29), we can obtain the steady-state equation
.Introducing (30) into (29), we can obtain the steady-state equation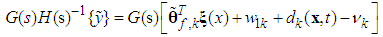 | (31) |
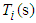 as
as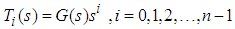 | (32) |
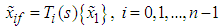 | (33) |
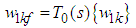 | (34) |
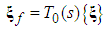 | (35) |
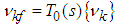 | (36) |
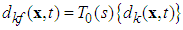 | (37) |
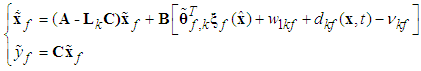 | (38) |
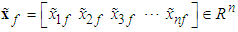
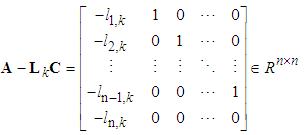 Define
Define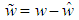 | (39) |
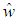 is the estimated of
is the estimated of 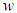 , and
, and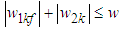 | (40) |
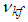 and the parameter update laws as follows:
and the parameter update laws as follows: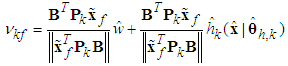 | (41) |
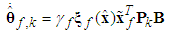 | (42) |
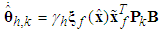 | (43) |
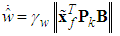 | (44) |
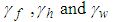 are positive constantsRemark 1: Without loss of generality, the adaptive laws used in this paper are assumed that the parameter vectors are within the constraint sets or on the boundaries of the constraint sets but moving toward the inside of the constraint sets. If the parameter vectors are on the boundaries of the constraint sets but moving toward the outside of the constraint sets, we have to use the projection algorithm to modify the adaptive laws such that the parameter vectors will remain inside of the constraint sets. Readers can refer to reference [16]. The proposed adaptive law (41)-(44) can be modified as the following form:
are positive constantsRemark 1: Without loss of generality, the adaptive laws used in this paper are assumed that the parameter vectors are within the constraint sets or on the boundaries of the constraint sets but moving toward the inside of the constraint sets. If the parameter vectors are on the boundaries of the constraint sets but moving toward the outside of the constraint sets, we have to use the projection algorithm to modify the adaptive laws such that the parameter vectors will remain inside of the constraint sets. Readers can refer to reference [16]. The proposed adaptive law (41)-(44) can be modified as the following form: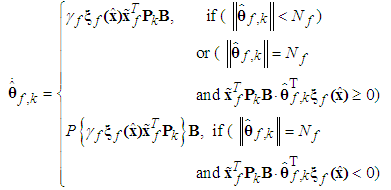 | (45) |
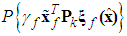 is defined as
is defined as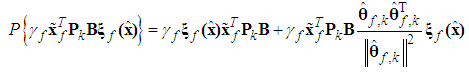 | (46) |
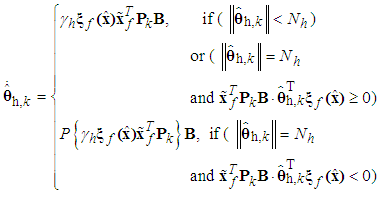 | (47) |
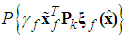 is defined as
is defined as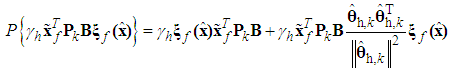 | (48) |
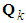 , if there exist symmetric positive definite matrix
, if there exist symmetric positive definite matrix 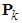 such that the following Lyapunov equation
such that the following Lyapunov equation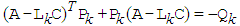 | (49) |
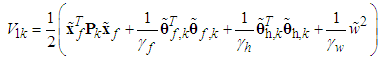 | (50) |
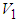 and the facts
and the facts 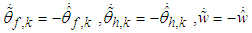 we obtain
we obtain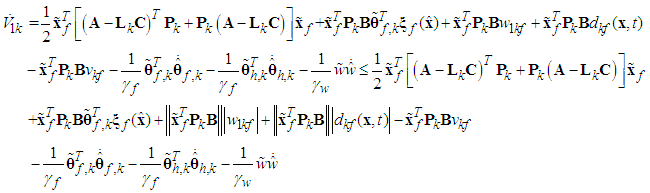 | (51) |
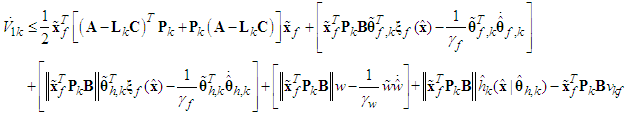 | (52) |
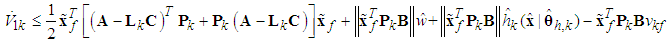 | (53) |
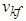 (41), the above equation can be rewritten as
(41), the above equation can be rewritten as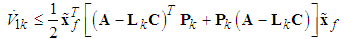 | (54) |
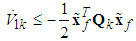 | (55) |
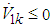 from (55), and the estimation errors of the closed-loop system converge to a neighborhood of zero based on Lyapunov synpaper approach. This completes the proof.
from (55), and the estimation errors of the closed-loop system converge to a neighborhood of zero based on Lyapunov synpaper approach. This completes the proof.3.2. Controller Design
- Next, we design the observer-based sliding mode controller. By employing (8) and (16), we get
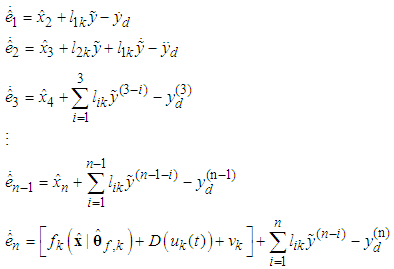 Define the sliding surfaces as follows:
Define the sliding surfaces as follows: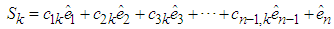 | (56) |
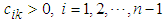 is designed parameters.Differentiating
is designed parameters.Differentiating 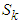 with respect to time, we have
with respect to time, we have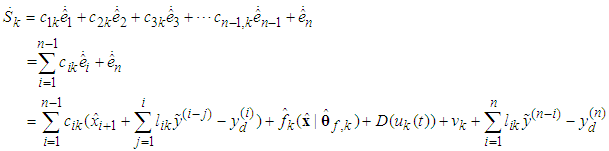 | (57) |
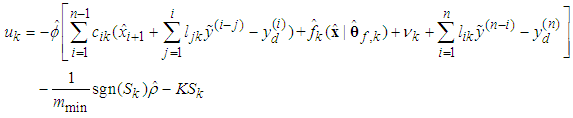 | (58) |
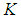 is a positive constant, and
is a positive constant, and 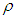 is defined in (7).We defined
is defined in (7).We defined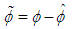 | (59) |
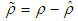 | (60) |
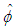 is the estimate of
is the estimate of 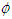 , which is defined as
, which is defined as 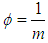 .
. 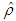 is the estimate of
is the estimate of 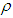 . The parameter update laws are as follows:
. The parameter update laws are as follows: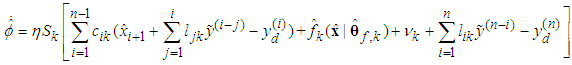 | (61) |
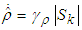 | (62) |
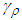 and
and 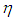 are positive constants, and
are positive constants, and 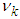 can be obtained by backward from
can be obtained by backward from 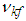 .Theorem 2: Consider the nonlinear switched system (1) with an unknown dead-zone input (4). The proposed observed-based fuzzy sliding mode controller defined by (58) guarantees that all signals of the closed-loop system are bounded and converge to a neighborhood of zero.Proof. Consider the Lyapunov function candidate
.Theorem 2: Consider the nonlinear switched system (1) with an unknown dead-zone input (4). The proposed observed-based fuzzy sliding mode controller defined by (58) guarantees that all signals of the closed-loop system are bounded and converge to a neighborhood of zero.Proof. Consider the Lyapunov function candidate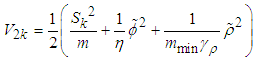 | (63) |
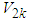 with the respect to time, we obtain
with the respect to time, we obtain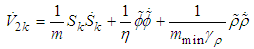 | (64) |
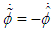 and
and 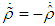 , the above equation becomes
, the above equation becomes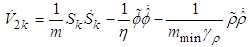 | (65) |
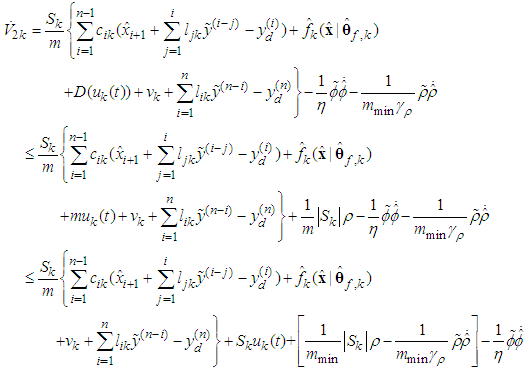 | (66) |
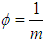 , the above equation (66) becomes
, the above equation (66) becomes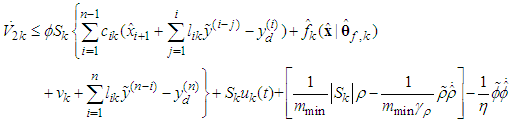 | (67) |
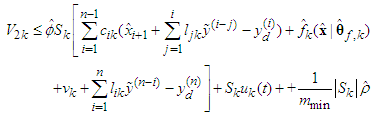 | (68) |
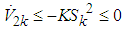 | (69) |
4. An Example and Simulation Results
- In this section, a mass-spring-damper system [12] in the presence of uncertain parameter and exogenous disturbances is considered as our simulation example in Fig. 2. The corresponding mathematical model is described as follows:
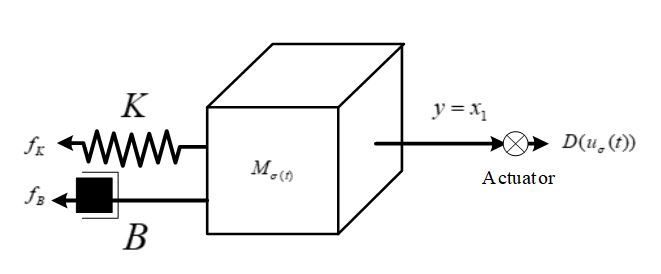 | Figure 2. The mass-spring-damper system |
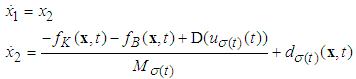 where
where 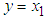 is the displacement of the mass,
is the displacement of the mass, 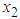 is the velocity of the mass,
is the velocity of the mass, 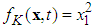 are the spring force,
are the spring force, 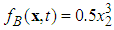 , are the friction force,
, are the friction force, 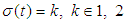 is the switched signal,
is the switched signal, 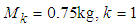 and
and 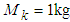 ,
, 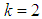 is the body mass, and
is the body mass, and 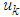 is the applied force. The structures of spring force and friction force are assumed to be known. The exogenous disturbance is assumed to be
is the applied force. The structures of spring force and friction force are assumed to be known. The exogenous disturbance is assumed to be 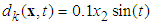 and
and 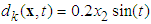 , In the implementation, five fuzzy sets are defined over interval [-3,3] for
, In the implementation, five fuzzy sets are defined over interval [-3,3] for  , with labels
, with labels 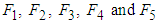 and their membership functions are
and their membership functions are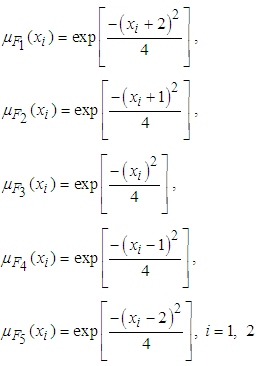 In this section, the control objective is to maintain the system output
In this section, the control objective is to maintain the system output 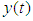 to follow the reference signal
to follow the reference signal 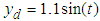 . First, we select the observer gain matrix as
. First, we select the observer gain matrix as 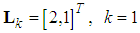 and
and 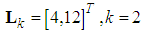 . In this example, the sampling time is 0.01s. The sliding surface are select as
. In this example, the sampling time is 0.01s. The sliding surface are select as 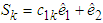 . when k=1
. when k=1 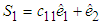 ,
, 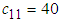 and when k = 2
and when k = 2 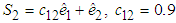 . The initial values are chosen as
. The initial values are chosen as 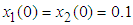 ,
, 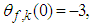
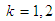 ,
,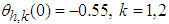 ,
, 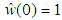 . The other parameters are selected as
. The other parameters are selected as 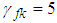 ,
, 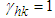 ,
,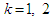 and
and 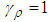 ,
, 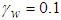 . The simulation is divided into two cases, one for the dwell time of 5 seconds and the other for the dwell time of 1 second. Finally, the simulation results are shown in Figs. 3-12.
. The simulation is divided into two cases, one for the dwell time of 5 seconds and the other for the dwell time of 1 second. Finally, the simulation results are shown in Figs. 3-12.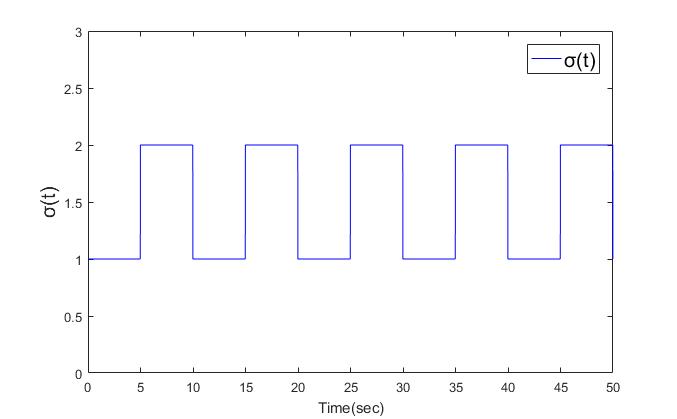 | Figure 3. The switched signal  with dwell time is 5secs with dwell time is 5secs |
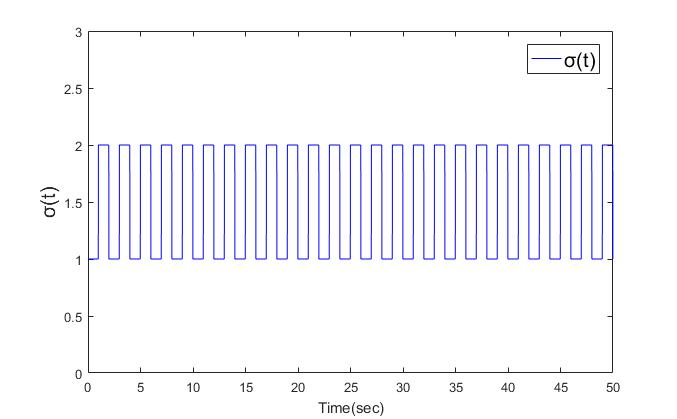 | Figure 4. The switched signal 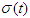 with dwell time is 1sec with dwell time is 1sec |
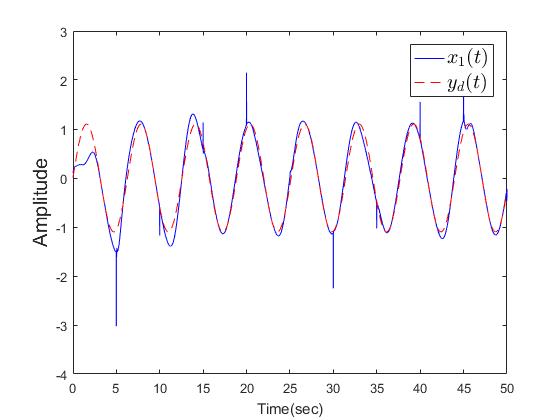 | Figure 5. The outputs 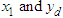 with dwell time is 5secs with dwell time is 5secs |
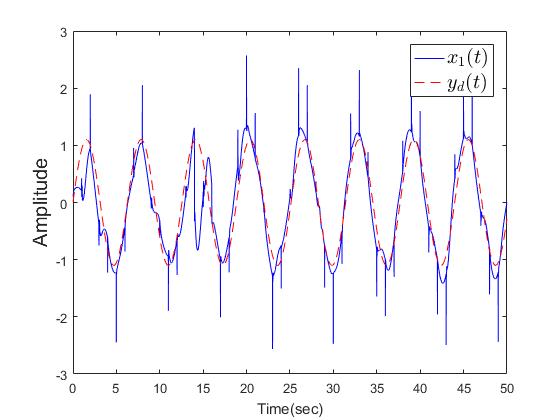 | Figure 6. The outputs 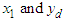 with dwell time is 1sec with dwell time is 1sec |
 | Figure 7. The trajectories of 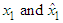 with dwell time is 5secs with dwell time is 5secs |
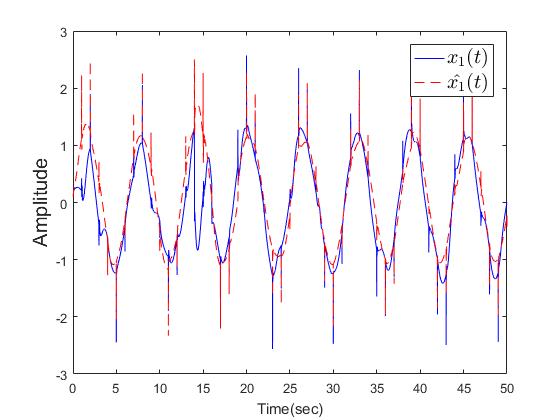 | Figure 8. The trajectories of 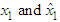 with dwell time is 1sec with dwell time is 1sec |
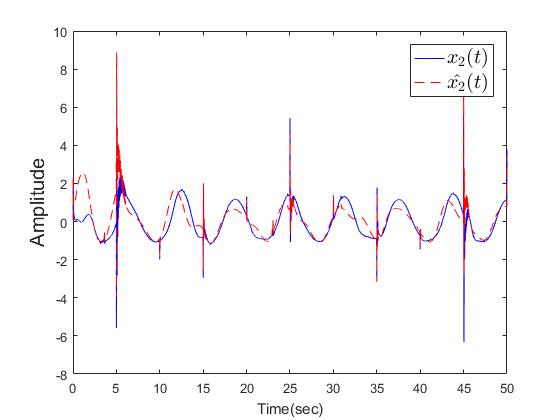 | Figure 9. The trajectories of 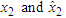 with dwell time is 5secs with dwell time is 5secs |
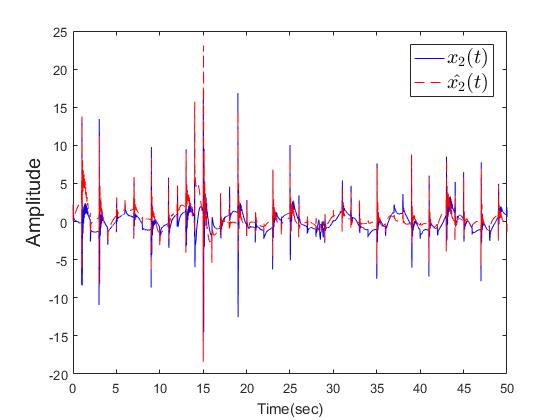 | Figure 10. The trajectories of 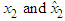 with dwell time is 1sec with dwell time is 1sec |
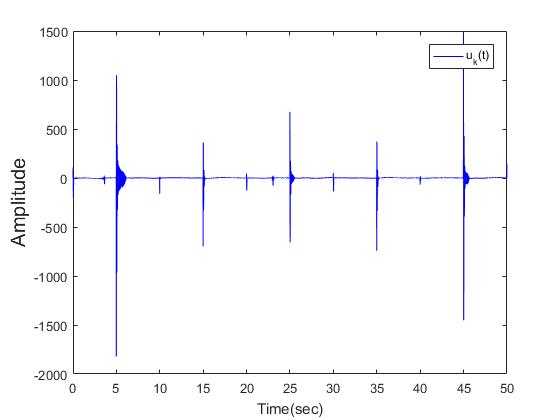 | Figure 11. The control signal 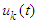 with dwell time is 5secs with dwell time is 5secs |
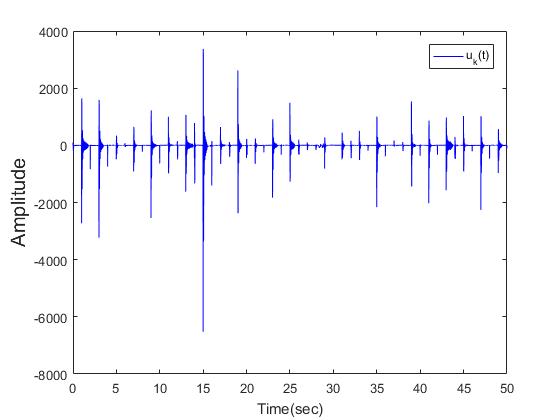 | Figure 12. The control signal 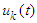 with dwell time is 1sec with dwell time is 1sec |
5. Conclusions
- An observer-based adaptive fuzzy sliding mode control approach has been proposed for a class of uncertain switched nonlinear systems with dead-zone input in strict-feedback form. A fuzzy state observer has been designed for estimating the unavailable states with the help of FLS approximating the unknown functions. Based on the designed sliding mode controller, the boundedness of the proposed sliding surfaces which realizes the stability of system can be ensured. By choosing an appropriate Lyapunov function, the proposed controller is designed to demonstrate that all the signals of the closed-loop system can not only guarantee uniformly ultimately bounded, but also achieve good tracking performance. Finally, some computer simulation results of a practical example are illustrated to verify the effectiveness of the proposed approach.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML