-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2019; 9(1): 15-25
doi:10.5923/j.control.20190901.03

Adaptive Model Reference Hierarchical Sliding Mode Control of Uncertain Underactuated Systems with Time Delay and Dead-Zone Input
Chiang-Cheng Chiang, Yu-Chih Chen
Department of Electrical Engineering, Tatung University, Taipei, Taiwan, Republic of China
Correspondence to: Chiang-Cheng Chiang, Department of Electrical Engineering, Tatung University, Taipei, Taiwan, Republic of China.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper focuses on a problem of adaptive model reference hierarchical sliding mode control for a class of uncertain underactuated systems with unknown dead-zone and time delay. An incremental hierarchical structure sliding-mode controller (IHSSMC) strategy based on the reference model is presented, which drives the system output to follow the reference model. Fuzzy logic systems are utilized to approximate the unknown nonlinear functions by some adaptive laws. An incremental hierarchical structure sliding-mode controller (IHSSMC) is developed by introducing the incremental hierarchical structure into sliding mode control (SMC) method. By choosing an appropriate Lyapunov–Krasovskii function, the proposed controller is designed to demonstrate that all the signals in the closed-loop system can not only guarantee uniformly ultimately bounded, but also achieve good tracking performance. Finally, some computer simulation results of a practical example are illustrated to verify the effectiveness of the proposed approach.
Keywords: Underactuated system, Lyapunov–Krasovskii function, Incremental hierarchical structure, Sliding mode control, Model reference control, Time delay, Dead-zone input, Fuzzy logic systems
Cite this paper: Chiang-Cheng Chiang, Yu-Chih Chen, Adaptive Model Reference Hierarchical Sliding Mode Control of Uncertain Underactuated Systems with Time Delay and Dead-Zone Input, International Journal of Control Science and Engineering, Vol. 9 No. 1, 2019, pp. 15-25. doi: 10.5923/j.control.20190901.03.
Article Outline
1. Introduction
- In the past two decades, underactuated systems have received much attention and some attractive results have been presented in the literature. Systems are said to be underactuated when the control actuators are fewer than number of degrees of freedom. They have more advantages in case of the reduced weight, cost, energy consumption, and the system structure design than actuated ones. Related problems have been presented in many actual systems such as, the crane system [1], underwater vehicles [2], the four-link manipulator [3], the axisymmetric spacecraft [4], hypersonic vehicles [5], the linear quadratic regulator (LQR) [6], the pendubot [7], the inertia-wheel pendulum (IWP) [8-10], and so on.Dead-zone input nonlinearity is a nonsmooth function that features certain insensitivity for small control inputs which is often encountered in a variety of practical systems such as the four-link PAAA (Passive-Active-Active-Active) manipulator, the single-link flexible joint manipulator, and so on. The work [11] investigated the position-posture control problem of a planar four-link underactuated manipulator. The problem of fuzzy adaptive control design and discretization for a class of nonlinear uncertain systems was studied in [12]. In [13], an observed-based adaptive fuzzy tracking controller has been presented for switched nonlinear systems with dead-zone.Fuzzy logic systems (FLSs) with appropriate adaptive laws and projection algorithms are introduced to approximate the unknown nonlinear functions appearing in the structure of the underactuated system. A FLS consists of four parts: the knowledge base, the fuzzifier, the fuzzy inference engine working on fuzzy rules, and the defuzzifier. By using Lyapunov-Krasovskii stability theorem, some adaptive laws are presented for fuzzy model and time delay.The sliding-mode control technique have some advantages such as insensitivity to system parameter variations, invariance to external disturbances, good transient performance, fast response, and so on. Basically, SMC laws comprise two parts: switching controller design and equivalent controller design. The switching control law is employed to lead the system’s states to a given sliding surface and the equivalent control law guarantees the system’s states to stay on the aforementioned sliding surface and converge to zero along the sliding surface. As a result of the underactuated characteristic of the controlled system, at least two sliding surfaces with specific relation are utilized for the controller design. The sliding-mode controller on the basis of the incremental hierarchical structure and aggregated hierarchical structure were used to deal with the under-actuated system. For the incremental hierarchical structure of a sliding-mode controller, one of the subsystems is defined as the first layer sliding surface. Next, the first-layer sliding surface and one of the left states are used to establish the second-layer sliding surface. The process continues till all the subsystems are included.The key idea of model reference hierarchical sliding mode control is motivated by the concept of model reference sliding mode control. The model reference hierarchical sliding mode control is to combine or integrate model reference and aforementioned hierarchical sliding mode control in such a way that the advantages of both techniques can be realized. In this paper, incremental hierarchical structure sliding-mode controller (IHSSMC) scheme based on reference model is proposed, which tracks the reference model by itself.In this paper, an adaptive model reference hierarchical sliding mode control method is developed for a class of uncertain underactuated systems with time delay and dead-zone input. A fuzzy logic system with adaptive laws is introduced to approximate the nonlinear functions appearing in the structure of the underactuated system. Choosing an appropriate Lyapunov-Krasovskii function, it is theoretically verified that all the signals in the closed-loop system are uniformly ultimately bounded under our designed adaptive model reference control method. By introducing a sliding-mode controller with incremental hierarchical structure, the errors between the system outputs and model reference outputs are driven onto the sliding surface and kept on the surface afterward.The rest of this paper is organized as follows. In Section II, the problem statement and basic preliminaries together with the definition of fuzzy logic systems (FLSs) are given. In Section III, the controller design based on the model reference hierarchical sliding mode control method is proposed to cope with the control problem of a class of uncertain underactuated nonlinear time-delay systems with dead-zone input. The stability analysis of the whole system is also verified by Lyapunov-Krasovskii functional. Simulation results are provided in Section IV to demonstrate the advantages and effectiveness of the proposed approaches. Finally, the concluding remarks are gathered in Section V.
2. Problem Statement and Preliminaries
2.1. System Description
- Consider a class of single-input-multi-output uncertain underactuated nonlinear systems with unknown dead-zone input and time delay as follows:
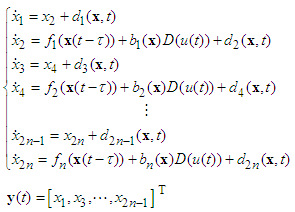 | (1) |
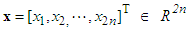 is the system state vector which is assumed to be available for measurement,
is the system state vector which is assumed to be available for measurement, 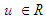 and
and 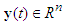 are input and output of the system output, respectively.
are input and output of the system output, respectively. 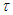 is the value of time delay.
is the value of time delay. 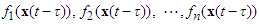 , and
, and 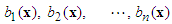 are unknown real continuous nonlinear functions,
are unknown real continuous nonlinear functions, 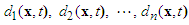 are unknown external bound disturbances.
are unknown external bound disturbances. 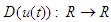 is the nonlinear input function containing a dead-zone. Without loss of generality, we assume that
is the nonlinear input function containing a dead-zone. Without loss of generality, we assume that 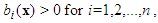 and the following assumptions are made for the controller design:Assumption 1: The time delay
and the following assumptions are made for the controller design:Assumption 1: The time delay 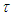 is a fixed and known constant.Assumption 2:
is a fixed and known constant.Assumption 2: 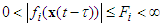 ,
, 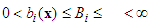 ,
, 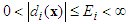 , for
, for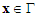
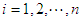 , where
, where 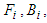 and
and 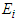 are known constants, and
are known constants, and 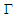 is a set given as follows:
is a set given as follows: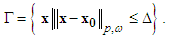 Here
Here  is a set of weight, and
is a set of weight, and  is a positive constant which denotes all state variables’ boundary.
is a positive constant which denotes all state variables’ boundary.  is a fixed point, and
is a fixed point, and 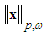 is a weighted p-norm, which is defined as
is a weighted p-norm, which is defined as If
If 
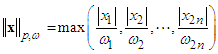 If
If 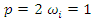 for
for 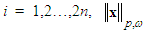 will denote Euclidean norm
will denote Euclidean norm 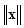 .The non-symmetric dead-zone with input
.The non-symmetric dead-zone with input 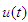 and output as shown in the above Fig. 1. is described by
and output as shown in the above Fig. 1. is described by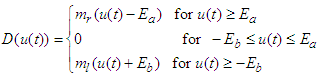 | (2) |
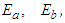 and
and 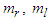 are parameters and slopes of the dead-zone, respectively.
are parameters and slopes of the dead-zone, respectively. | Figure 1. Dead-zone model |
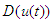 is not available to obtain.Assumption 4: The coefficients
is not available to obtain.Assumption 4: The coefficients  , and
, and 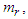
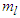 are unknown.Assumption 5: There exist known constants
are unknown.Assumption 5: There exist known constants 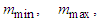
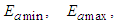
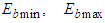 such that the unknown dead-zone parameters
such that the unknown dead-zone parameters 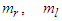 ,
, 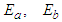 are bounded, i.e.
are bounded, i.e. 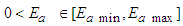 ,
, 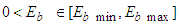 ,
, 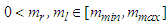 Based on the above assumptions the expression (2) can be represented as
Based on the above assumptions the expression (2) can be represented as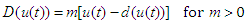 | (3) |
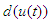 can be calculated form (2) and (3) as
can be calculated form (2) and (3) as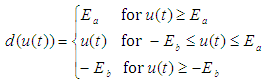 | (4) |
 is bounded, and satisfies:
is bounded, and satisfies: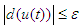 | (5) |
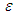 is an upper bound, which can be chosen as
is an upper bound, which can be chosen as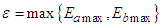 | (6) |
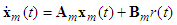 | (7) |
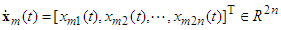 is the state vector of reference model,
is the state vector of reference model, 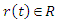 is the bounded reference input.
is the bounded reference input. 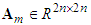 is Hurwitz. Let the model reference output vector as
is Hurwitz. Let the model reference output vector as 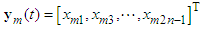 . Because the underactuated system is divided into several different subsystems and for the state variables, there is not obvious differential relationship between these subsystems. As the result,
. Because the underactuated system is divided into several different subsystems and for the state variables, there is not obvious differential relationship between these subsystems. As the result, 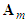 comprises n subsystems with the controllable canonical form for the plant.Thus,
comprises n subsystems with the controllable canonical form for the plant.Thus, | (8) |
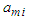 for
for 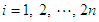 are positive real constants to be chosen.
are positive real constants to be chosen.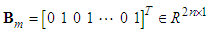 | (9) |
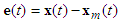 | (10) |
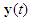 would track the reference model output vector
would track the reference model output vector 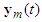 . Define the vector of the output tracking error as
. Define the vector of the output tracking error as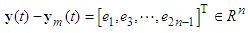 | (11) |
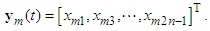 | (12) |
2.2. Description of Fuzzy Logic Systems
- The fuzzy logic system performs a mapping from
 to
to  . Let
. Let  where
where 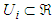 ,
, 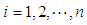 . The fuzzy rule base consists of a collection of fuzzy IF-THEN rules:
. The fuzzy rule base consists of a collection of fuzzy IF-THEN rules: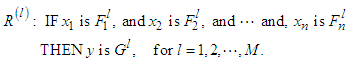 | (13) |
 and
and 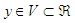 are the input and output of the fuzzy logic system,
are the input and output of the fuzzy logic system, 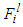 and
and  are fuzzy sets in
are fuzzy sets in 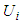 and
and 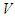 , respectively. The fuzzifier maps a crisp point
, respectively. The fuzzifier maps a crisp point 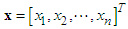 into a fuzzy set in
into a fuzzy set in 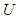 . The fuzzy inference engine performs a mapping from fuzzy sets in
. The fuzzy inference engine performs a mapping from fuzzy sets in 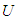 to fuzzy sets in
to fuzzy sets in 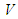 , based upon the fuzzy IF-THEN rules in the fuzzy rule base and the compositional rule of inference. The defuzzifier maps a fuzzy set in
, based upon the fuzzy IF-THEN rules in the fuzzy rule base and the compositional rule of inference. The defuzzifier maps a fuzzy set in 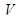 to a crisp point in
to a crisp point in 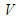 .The fuzzy systems with center-average defuzzifier, product inference and singleton fuzzifier are of the following form:
.The fuzzy systems with center-average defuzzifier, product inference and singleton fuzzifier are of the following form: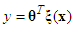 | (14) |
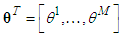 with each variable
with each variable 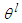 as the point at which the fuzzy membership function of
as the point at which the fuzzy membership function of  achieves the maximum value and
achieves the maximum value and 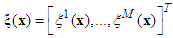 with each variable
with each variable 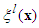 as the fuzzy basis function defined as
as the fuzzy basis function defined as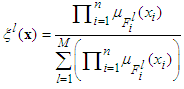 | (15) |
 is the membership function of the fuzzy set.
is the membership function of the fuzzy set.3. Controller Design and Stability Analysis
- From (7), the model reference of system can be rewritten as follows:
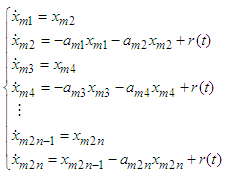 | (16) |
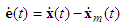 | (17) |
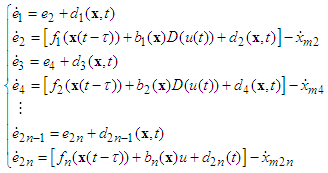 | (18) |
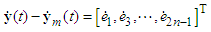 | (19) |
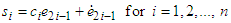 | (20) |
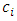 are positive constants.Differentiating
are positive constants.Differentiating 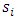 with respect to time, we have
with respect to time, we have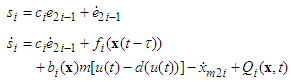 | (21) |
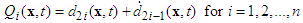 Assumption 6:
Assumption 6: 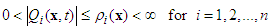 where
where 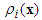 are unknown positive smooth continuous functions.According to the equivalent control method, the equivalent control law of the systems can be obtained as:
are unknown positive smooth continuous functions.According to the equivalent control method, the equivalent control law of the systems can be obtained as: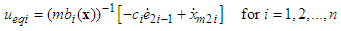 | (22) |
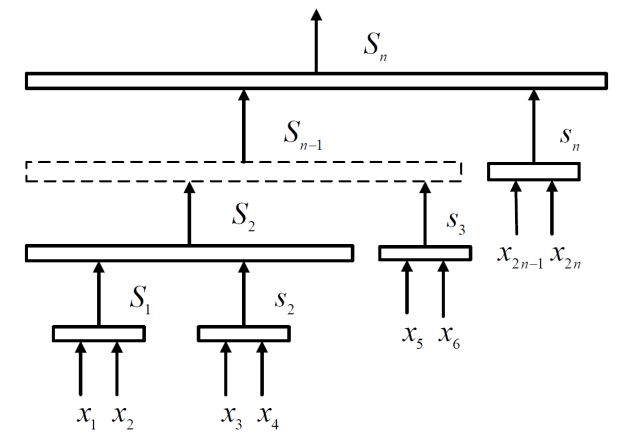 | Figure 2. Hierarchical structure of sliding surfaces |

 and
and  can be approximated, over a compact set
can be approximated, over a compact set  by using the fuzzy logic systems as follows:
by using the fuzzy logic systems as follows: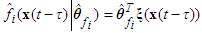 | (23) |
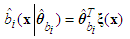 | (24) |
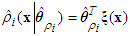 | (25) |
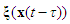 and
and 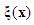 are the fuzzy basis vector,
are the fuzzy basis vector, 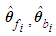 and
and 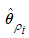 for
for 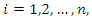 are the corresponding adjustable parameter vector of each fuzzy logic systems. It is assumed that
are the corresponding adjustable parameter vector of each fuzzy logic systems. It is assumed that  and
and 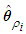 belong to compact sets
belong to compact sets 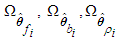 , respectively, which are defined as:
, respectively, which are defined as: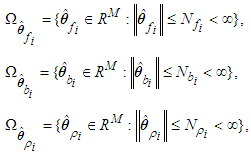 where
where 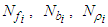 for
for 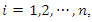 are the designed parameters, and M is the number of fuzzy inference rules. Let us define the optimal parameter vectors,
are the designed parameters, and M is the number of fuzzy inference rules. Let us define the optimal parameter vectors, 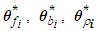 for
for 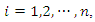 as follows:
as follows: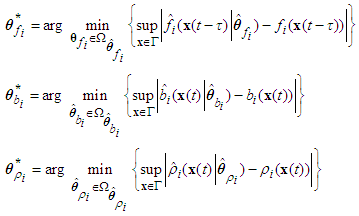 where
where 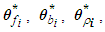 for
for 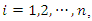 are bounded in the suitable closed sets
are bounded in the suitable closed sets 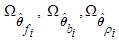 , respectively. The parameter estimation errors can be defined as:
, respectively. The parameter estimation errors can be defined as: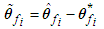 | (26) |
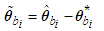 | (27) |
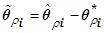 | (28) |
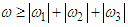 | (29) |
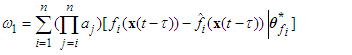 | (30) |
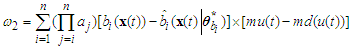 | (31) |
 | (32) |
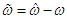 | (33) |
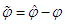 | (34) |
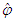 is an estimate of
is an estimate of  , which is defined as
, which is defined as 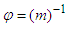 , and
, and 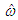 be as the estimate of
be as the estimate of 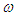 .Based on the fuzzy logic systems, the equation (22) can be replaced as the following controller:
.Based on the fuzzy logic systems, the equation (22) can be replaced as the following controller: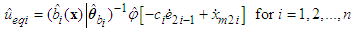 | (35) |
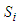 and its control law
and its control law 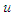 can be defined as follows.
can be defined as follows.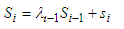 | (36) |
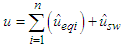 | (37) |
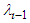 for
for 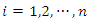 are positive constants;
are positive constants; 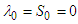 . From the recursive formulas (36), we have
. From the recursive formulas (36), we have | (38) |
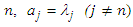 is a constant, and
is a constant, and 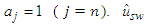 is the switching control of sliding surface can be chosen as.
is the switching control of sliding surface can be chosen as.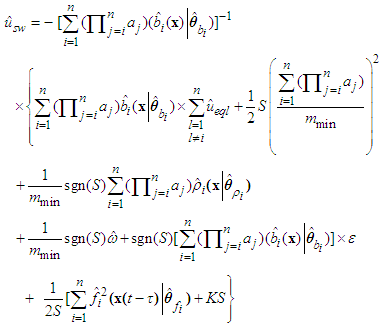 | (39) |
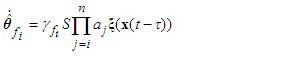 | (40) |
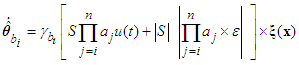 | (41) |
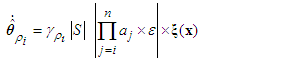 | (42) |
 | (43) |
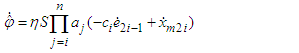 | (44) |
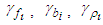 for
for 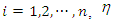 and
and 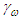 are positive constants.Remark 1: Without loss of generality, the adaptive laws used in this paper are assumed that the parameter vectors are within the constraint sets or on the boundaries of the constraint sets but moving toward the inside of the constraint sets. If the parameter vectors are on the boundaries of the constraint sets but moving toward the outside of the constraint sets, we have to use the projection algorithm to modify the adaptive laws such that the parameter vectors will remain inside of the constraint sets. Readers can refer to reference [14]. The proposed adaptive laws (40)-(44) can be modified as the following form:
are positive constants.Remark 1: Without loss of generality, the adaptive laws used in this paper are assumed that the parameter vectors are within the constraint sets or on the boundaries of the constraint sets but moving toward the inside of the constraint sets. If the parameter vectors are on the boundaries of the constraint sets but moving toward the outside of the constraint sets, we have to use the projection algorithm to modify the adaptive laws such that the parameter vectors will remain inside of the constraint sets. Readers can refer to reference [14]. The proposed adaptive laws (40)-(44) can be modified as the following form: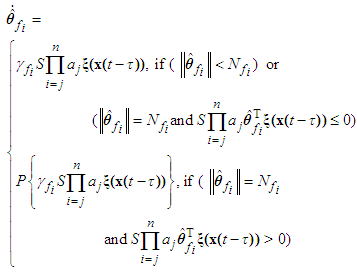 | (45) |
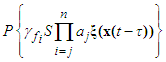 is defined as
is defined as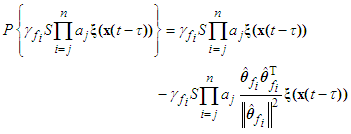 | (46) |
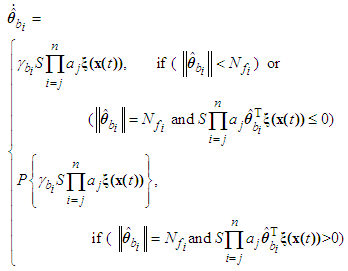 | (47) |
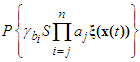 is defined as
is defined as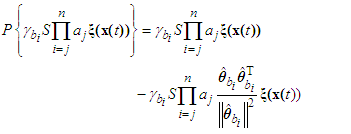 | (48) |
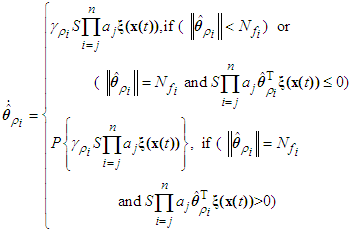 | (49) |
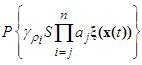 is defined as
is defined as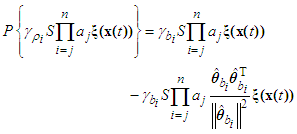 | (50) |
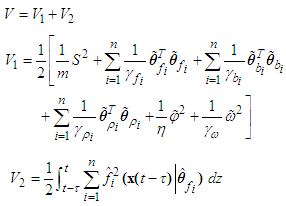 | (51) |
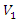 with respect to time, and by the fact
with respect to time, and by the fact 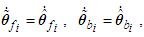
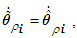
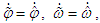 we can obtain.
we can obtain.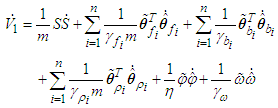 According to (38), and (21), we have
According to (38), and (21), we have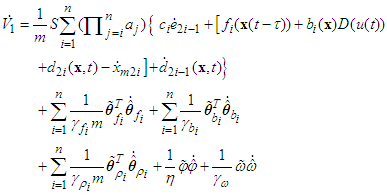 | (52) |
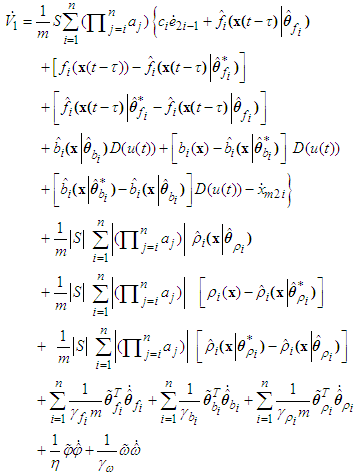 | (53) |
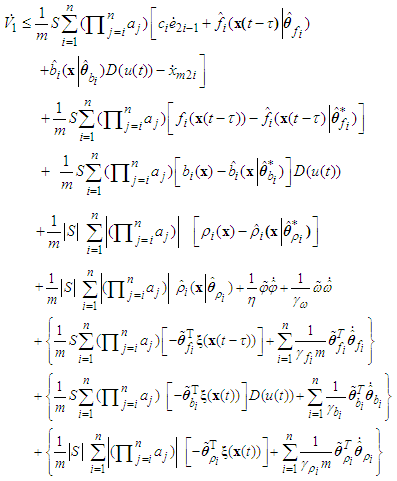 | (54) |
 According to (27), the above equation can be rewritten as
According to (27), the above equation can be rewritten as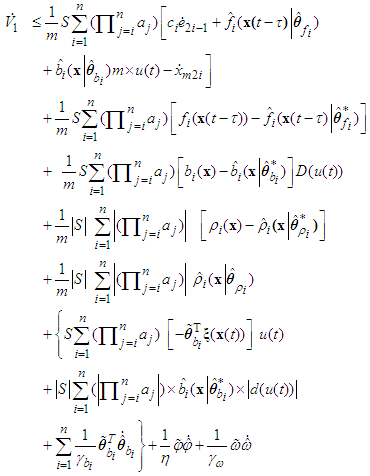 | (55) |
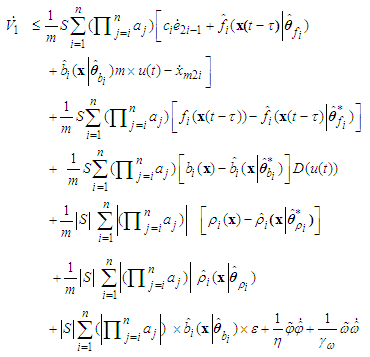 According to (29)-(33) and (43), we obtain
According to (29)-(33) and (43), we obtain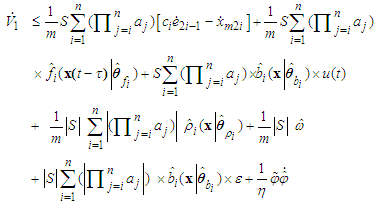 | (56) |
 for scalars a and b, we obtain
for scalars a and b, we obtain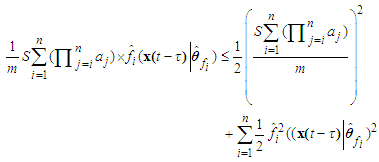 | (57) |
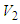 with respect to time, we can obtain
with respect to time, we can obtain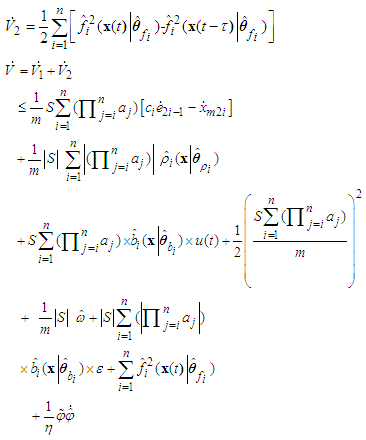 According to (34) (37) and (44), we have
According to (34) (37) and (44), we have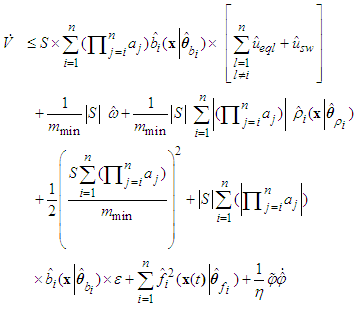 Using the switching control laws (37), the above equation can be rewritten as
Using the switching control laws (37), the above equation can be rewritten as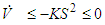 Therefore, the hierarchical sliding surface S is stable, and the all signals of the closed-loop system are bounded based on the proposed controller. This completes the proof.
Therefore, the hierarchical sliding surface S is stable, and the all signals of the closed-loop system are bounded based on the proposed controller. This completes the proof.4. An Example and Simulation Results
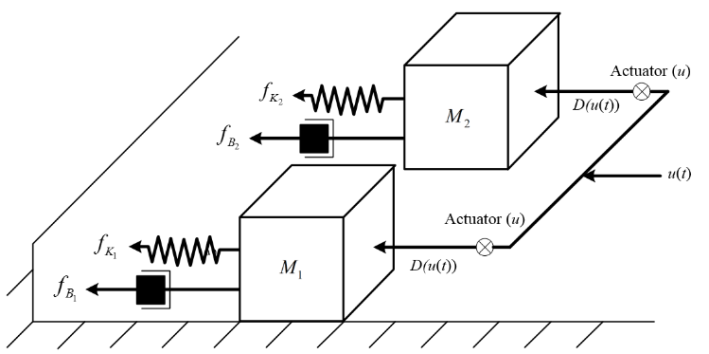
- In this section, a mass-spring-damper system [15] in the presence of uncertain parameter and exogenous disturbances is considered as our simulation example Fig. 3. The corresponding mathematical model is described as follows:
 | Figure 3. The mass-spring-damper system |
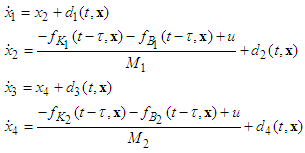 where
where 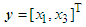 is the displacement of the mass,
is the displacement of the mass, 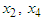 is the velocity of the mass,
is the velocity of the mass, 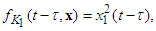
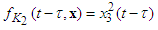 are the spring force,
are the spring force, 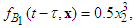
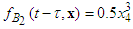 are the friction force,
are the friction force, 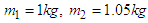 is the body mass, and
is the body mass, and 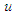 is the applied force. The structures of spring force and friction force are assumed to be known. The exogenous disturbance is assumed to be
is the applied force. The structures of spring force and friction force are assumed to be known. The exogenous disturbance is assumed to be 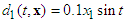 ,
, 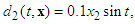

 .
. 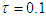 sec is time delay. In the implementation, six fuzzy sets are defined over interval [-3,3] for
sec is time delay. In the implementation, six fuzzy sets are defined over interval [-3,3] for 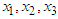 and
and 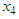 , with labels NB,NM,NS,PS,PM, and PB, and their membership functions are
, with labels NB,NM,NS,PS,PM, and PB, and their membership functions are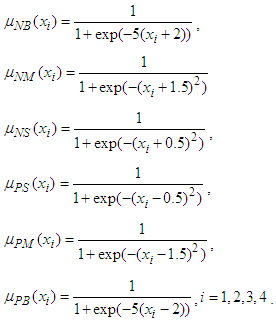 , We apply the robust model reference sliding mode control approach in Section 3 to deal with control problem. The system matrices of reference model are given as follows:
, We apply the robust model reference sliding mode control approach in Section 3 to deal with control problem. The system matrices of reference model are given as follows: 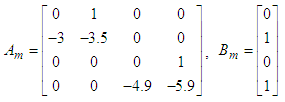 and the reference input
and the reference input 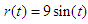 .The control object is to maintain the system output
.The control object is to maintain the system output 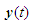 to follow the reference model
to follow the reference model 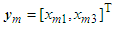 . In the case, the first level sliding surface
. In the case, the first level sliding surface and
and 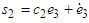 , where
, where 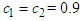 , the hierarchical sliding surface is constructed as
, the hierarchical sliding surface is constructed as 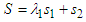 , where
, where 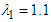 . The initial values are chosen as
. The initial values are chosen as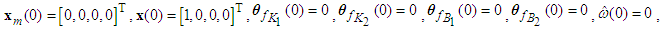
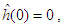
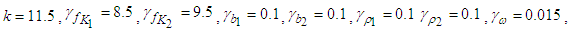
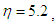 and the boundary layer
and the boundary layer 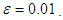 The simulation results are shown in Figs. 4-6. Fig.4 and Fig.5 reveal that the state trajectories, respectively. The control signal is shown in Figs. 6. The simulation results verify the usefulness of the proposed adaptive model reference hierarchical sliding-mode controller.
The simulation results are shown in Figs. 4-6. Fig.4 and Fig.5 reveal that the state trajectories, respectively. The control signal is shown in Figs. 6. The simulation results verify the usefulness of the proposed adaptive model reference hierarchical sliding-mode controller.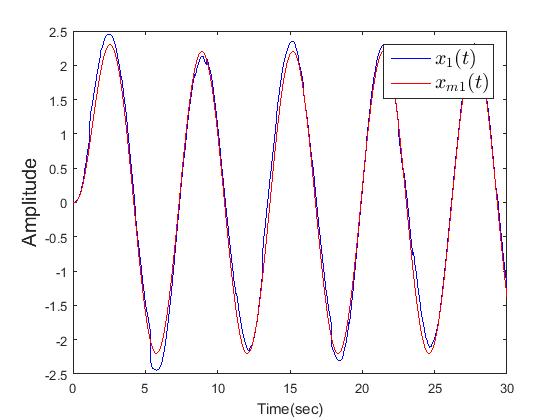 | Figure 4. The trajectories of state 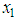 and state of reference model and state of reference model  |
 | Figure 5. The trajectories of state 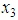 and state of reference model and state of reference model 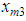 |
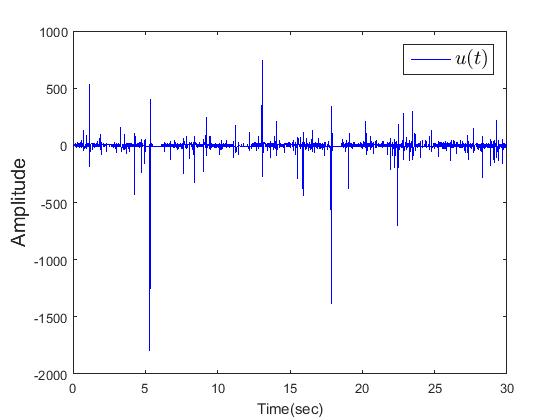 | Figure 6. The control signal u |
5. Conclusions
- This paper proposes an adaptive model reference hierarchical sliding mode control scheme for a class of uncertain underactuated systems that guarantees the closed-loop stability in presence of unknown input dead-zone and time delay. Fuzzy logic systems are used to approximate the unknown nonlinear functions by some adaptive laws. Based on the Lyapunov-Krasovskii stability theorem, the proposed incremental hierarchical structure sliding-mode controller not only guarantees the stability of the uncertain nonlinear state time-delay systems with input dead-zone, but also ensures good tracking performance. Finally, some simulation results of a practical example are illustrated to show the effectiveness of the proposed control method.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML