| [1] | Chasles, M. (1830). "Note sur les propriétés générales du système de deux corps semblables entr'eux". Bulletin des Sciences Mathématiques, Astronomiques, Physiques et Chemiques (in French). 14: 321–326. |
| [2] | Isaac Newton, 1642-1727. Newton's Principia: The Mathematical Principles of Natural Philosophy. New-York: Daniel Adee, 1846. |
| [3] | Leonhard Eulero. (Euler) Formulae generales pro translatione quacunque corporum rigidorum (General formulas for the translation of arbitrary rigid bodies), presented to the St. Petersburg Academy on October 9, 1775, and first published in Novi Commentarii academiae scientiarum Petropolitanae 20, 1776, pp. 189–207 (E478) and was reprinted in Theoria motus corporum rigidorum, ed. nova, 1790, pp. 449–460 (E478a) and later in his collected works Opera Omnia, Series 2, Volume 9, pp. 84–98. (https://math.dartmouth.edu/~euler/docs/originals/E478.pdf) |
| [4] | William Thompson, Peter Tait, Elements of Natural Philosophy, Cambridge, 1872. |
| [5] | Reuleaux, F.; Kennedy, Alex B. W. The Kinematics of Machinery: Outlines of a Theory of Machines, London: Macmillan, 1876; (https://archive.org/details/kinematicsofmach00reuluoft). |
| [6] | William Thomson Kelvin & Peter Guthrie Tait. Elements of Natural Philosophy, Cambridge University Press, 1894; p. 4. |
| [7] | Thomas Wallace Wright (1896). Elements of Mechanics Including Kinematics, Kinetics and Statics, D. Van Nostrand Company, Harvard University, 1896. |
| [8] | Merz, John (1903). A History of European Thought in the Nineteenth Century, Blackwood, London. p. 5. |
| [9] | Edmund Whittaker, A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, Cambridge University Press, 1904, 1937. |
| [10] | Irving Porter Church Mechanics of Engineering, Wiley, New York, 1908; p. 111. |
| [11] | Thomas Wright, Elements of Mechanics Including Kinematics, Kinetics, and Statics, With Applications, Nostrand, New York, 1909. |
| [12] | Eduard Study (D.H. Delphenich translator), Foundations and goals of analytical kinematics. Sitzber. d. Berl. math. Ges. 1913, 13, 36-60. Available online at (accessed on 14 Apr 2017), http://neo-classical-physics.info/uploads/3/4/3/6/34363841/study-analytical_kinematics.pdf. |
| [13] | Gray, Andrew (1918), A Treatise on Gyrostatics and Rotational Motion, MacMillan, London, 1918 (published 2007 as ISBN 978-1-4212-5592-7). |
| [14] | Rose, M. E. (1957), Elementary Theory of Angular Momentum, New York, NY: John Wiley & Sons (published 1995), ISBN 978-0-486-68480-2. |
| [15] | Thomas Kane, Analytical Elements of Mechanics Volume 1, Academic Press, New York and London, 1959. |
| [16] | Thomas Kane, Analytical Elements of Mechanics Volume 2 Dynamics, Academic Press, New York and London, 1961. |
| [17] | William Thompson, Space Dynamics, Wiley and Sons, New York, 1961. |
| [18] | Donald Greenwood, Principles of Dynamics, Prentice-Hall, Englewood Cliffs, 1965 (reprinted in 1988 as 2nd ed.), ISBN: 9780137089741. |
| [19] | Ai Chzcn Fung and Benjumin G. Zimmermun (1969). Digital Simulation of Rotational Kinematics. NASA Technical Report NASA TN D-5302. October 1969. Washington, D.C. (https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19690029793.pdf). |
| [20] | D.M. Henderson (1977). Euler Angles, Quaternions, and Transformation Matrices – Working Relationships. McDonnell Douglas Technical Services Co. Inc., as NASA Technical Report NASA-TM-74839. July 1977. (https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770024290.pdf). |
| [21] | D.M. Henderson (1977). Euler Angles, Quaternions, and Transformation Matrices – Working Relationships. McDonnell Douglas Technical Services Co. Inc., as NASA Technical Report NASA-TM-74839. July 1977. (https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770024290.pdf). |
| [22] | D.M. Henderson (1977). Euler Angles, Quaternions, and Transformation Matrices for Space Shuttle Analysis. McDonnell Douglas Technical Services Co. Inc., Houston Astronautics Division as NASA Design Note 1.4-8-020, 9 June 1977. (https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770019231.pdf). |
| [23] | Herbert Goldstein, Classical Mechanics 2nd Ed., Addison-Wesley, Massachusetts, 1981. |
| [24] | Thomas Kane, David Levinson, Dynamics: Theory and Application, McGraw-Hill, 1985. |
| [25] | Peter Huges, Spacecraft Attitude Dynamics, Wiley and Sons, New York, 1986. |
| [26] | William Wiesel, Spaceflight Dynamics, 2nd ed., Irwin McGraw-Hill, Boston, 1989, 1997. |
| [27] | Bong Wie, Space Vehicle Dynamics and Control, AIAA, Virginia, 1998. |
| [28] | Gregory G Slabaugh (1999). Computing Euler angles from a rotation matrix. 6(2000) 39-63. January 1999. (http://www.close-range.com/docspacecraftomputing_Euler_angles_from_a_rotation_matrix.pdf). |
| [29] | David Vallado, Fundamentals of Astrodynamics and Applications, 2nd ed., Microcosm Press, El Segundo, 2001. |
| [30] | Carlos Roithmayr, Dewey Hodges, Dynamics: Theory and Application of Kane’s Method, Cambridge, New York, 2016. |
| [31] | Timothy Sands, Richard Mihalik. Outcomes of the 2010 and 2015 nonproliferation treaty review conferences. World J. Soc. Sci. Humanities, 2: 46-51, 2016. DOI: 10.12691/wjssh-2-2-4. |
| [32] | Sands, T., 2016. Strategies for combating Islamic state. Soc. Sci., 5: 39-39. DOI: 10.3390/socsci5030039. |
| [33] | Mihalik, R., H. Camacho and T. Sands, 2017. Continuum of learning: Combining education, training and experiences. Education, 8: 9-13. DOI: 10.5923/j.edu.20180801.03. |
| [34] | Timothy Sands, Harold Camacho and Richard Mihalik, 2017. Education in nuclear deterrence and assurance. J. Def. Manag., 7: 166-166. DOI: 10.4172/2167-0374.1000166. |
| [35] | Timothy Sands, Richard Mihalik, (2018). Theoretical Context of the Nuclear Posture Review. Journal of Social Sciences, 14(1) 124-128, DOI 10.3844/jssp.2018.124.128. (http://thescipub.com/pdf/10.3844/jssp.2018.124.128)Sands, T, 2009. Satellite electronic attack of enemy air defenses. Proc. IEEE CDC. 434-438. DOI: 10.1109/SECON.2009.5174119. |
| [36] | Timothy Sands, 2018. Space mission analysis and design for electromagnetic suppression of radar. Intl. J. Electromag. and Apps., 8: 1-25. DOI: 10.5923/j.ijea.20180801.01. |
| [37] | Timothy Sands, Danni Lu, Janhwa Chu, Baolin Cheng, Developments in Angular Momentum Exchange, International Journal of Aerospace Sciences, Vol. 6 No. 1, 2018, pp. 1-7. doi: 10.5923/j.aerospace.20180601.01. |
| [38] | Timothy Sands, Jae Kim, Brij Agrawal., 2006. 2H Singularity free momentum generation with non-redundant control moment gyroscopes. Proc. IEEE CDC. 1551-1556. DOI: 10.1109/CDC.2006.377310. |
| [39] | Timothy Sands, Fine Pointing of Military Spacecraft. Ph.D. Dissertation, Naval Postgraduate School, Monterey, CA, USA, 2007. |
| [40] | Jae Kim, Timothy Sands, Brij Agrawal, 2007. Acquisition, tracking, and pointing technology development for bifocal relay mirror spacecraft. Proc. SPIE, 6569. DOI: 10.1117/12.720694. |
| [41] | Timothy Sands, Jae Kim, Brij Agrawal, 2009. Control moment gyroscope singularity reduction via decoupled control. Proc. IEEE SEC. 1551-1556. DOI: 10.1109/SECON.2009.5174111. |
| [42] | Timothy Sands, Jae Kim, Brij Agrawal, 2012. Nonredundant single-gimbaled control moment gyroscopes. J. Guid. Dyn. Contr. 35: 578-587. DOI: 10.2514/1.53538. |
| [43] | Timothy Sands, Jae Kim, Brij Agrawal, 2016. Experiments in Control of Rotational Mechanics. Intl. J. Auto. Contr. Intel. Sys., 2: 9-22. ISSN: 2381-7534. |
| [44] | Brij Agrawal, Jae Kim, Timothy Sands, “Method and apparatus for singularity avoidance for control moment gyroscope (CMG) systems without using null motion”, U.S. Patent 9567112 B1, Feb 14, 2017. |
| [45] | Timothy Sands, Jae Kim, Brij Agrawal, 2018. Singularity Penetration with Unit Delay (SPUD). Mathematics, 6: 23-38. DOI: 10.3390/math6020023. |
| [46] | Timothy Sands, Robert Lorenz, “Physics-Based Automated Control of Spacecraft” Proceedings of the AIAA Space 2009 Conference and Exposition, Pasadena, CA, USA, 14–17 September 2009. |
| [47] | Timothy Sands, 2012. Physics-based control methods. Adv. Space. Sys. Orb. Det., InTech, London. DOI: 10.5772/2408. |
| [48] | Timothy Sands, “Improved Magnetic Levitation via Online Disturbance Decoupling”, Physics Journal, 1(3) 272-280, 2015. |
| [49] | Scott Nakatani, 2014. Simulation of spacecraft damage tolerance and adaptive controls, Proc. IEEE Aero., 1-16. DOI: 10.1109/AERO.2014.6836260. |
| [50] | Scott Nakatani, 2016. Autonomous damage recovery in space. Intl. J. Auto. Contr. Intell. Sys., 2(2): 22-36. ISSN Print: 2381-75. |
| [51] | Scott Nakatani, 2018. Battle-damage tolerant automatic controls. Elec. and Electr. Eng., 8: 10-23. DOI: 10.5923/j.eee.20180801.02. |
| [52] | Peter Heidlauf, Matthew Cooper, “Nonlinear Lyapunov Control Improved by an Extended Least Squares Adaptive Feed forward Controller and Enhanced Luenberger Observer”, In Proceedings of the International Conference and Exhibition on Mechanical & Aerospace Engineering, Las Vegas, NV, USA, 2–4 October 2017. |
| [53] | Matthew Cooper, Peter Heidlauf, Timothy Sands, 2017. Controlling Chaos—Forced van der Pol Equation. Mathematics on Automation Control Systems, a special issue of Mathematics, 5: 70-80. DOI: 10.3390/math5040070. |
| [54] | Timothy Sands, “Phase Lag Elimination At All Frequencies for Full State Estimation of Spacecraft Attitude”, Physics Journal, 3(1) 1-12, 2017. |
| [55] | Timothy Sands, 2017. Nonlinear-adaptive mathematical system identification. Computation. 5:47-59. DOI: 10.3390/computation5040047. |
| [56] | Timothy Sands, Thomas Kenny, 2017. Experimental piezoelectric system identification, J. Mech. Eng. Auto, 7: 179-195. DOI: 10.5923/j.jmea.20170706.01. |
| [57] | Timothy Sands, 2017. Space systems identification algorithms. J. Space Expl. 6: 138-149. ISSN: 2319-9822. |
| [58] | Timothy Sands, “Experimental Sensor Characterization”, Journal of Space Exploration, 7(1) 140, 2018. |
| [59] | Timothy Sands, Armani, C., 2018. Analysis, correlation, and estimation for control of material properties. J. Mech. Eng. Auto. 8: 7-31, DOI: 10.5923/j.jmea.20180801.02. |
| [60] | Timothy Sands, 2009. Satellite Electronic Attack of Enemy Air Defenses. Proc. IEEE SEC, 434-438. |
| [61] | “Remarks by President Trump at a Meeting with the National Space Council and Signing of Space Policy Directive-3”, Available online at the White House’s online news website: https://0x9.me/1SoZk (Accessed 20 June 2018). |
| [62] | Jack Kuipers, “Quaternions and Rotation Sequences, Geometry, Integrability, and Quantization”, Sept 1-10, 1999 Varna, Bulgaria; Coral Press, Sofia, 2000. |
| [63] | Brendan Smeresky, Alex Rizzo, 2018. Kinematics in the Information Age. Mathematics and Engineering, special issue in Mathematics. 6(9) 148. Doi: 10.3390/math6090148. |
| [64] | Weisstein, Eric W. "Taylor Series. From MathWorld- A Wolfram Web Resource www.mathworld.wolfram.com/TaylorSeries.html. |
| [65] | Baczynski, Michael. Fast and Accurate Sine/Cosine Approximation, 18 July 2007, www.lab.polygonal.de/2007/07/18/fast-and-accurate-sinecosine-approximation/. |
| [66] | Timothy Sands, 2018. Electric Vehicle Sales Catastrophe Averted by Deterministic Artificial Intelligence Methods. Applied Sciences, submitted to Volume (8), 2081. |
| [67] | Lucas Bittick, Timothy Sands, “Political Rhetoric or Policy Shift: A Contextual Analysis of the Pivot to Asia”, Journal of Social Sciences, submitted to Volume (14) 2018. |
| [68] | Kyle Baker, Peter Heidlauf, Matthew Cooper, Timothy Sands. Autonomous trajectory generation for deterministic artificial intelligence. Electrical and Electronic Engineering, submitted to volume (8), 2018. |
| [69] | Timothy Sands, “Derivative Analysis of global average temperatures”, Climate, submitted to Volume (6), 2018. |


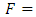
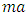 and rotations in accordance with Euler’s Moment Equations
and rotations in accordance with Euler’s Moment Equations 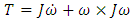 [9] (both equations named subsequent to Chasle’s expression), where m is the mass of the object and [J] is a matrix of mass moments of inertia very well explained by Kane [24]. Thus, unplanned changes in the components of [J] are deleterious since the control force F applied as a torque is designed for the formerly assumed [J].Investigation of motion without consideration of the nature of the body moved or how the motion is produced is called Phoronomics, or “the laws of going”, or more commonly but less properly kinematics [12], to be briefly discussed in section 2.3.
[9] (both equations named subsequent to Chasle’s expression), where m is the mass of the object and [J] is a matrix of mass moments of inertia very well explained by Kane [24]. Thus, unplanned changes in the components of [J] are deleterious since the control force F applied as a torque is designed for the formerly assumed [J].Investigation of motion without consideration of the nature of the body moved or how the motion is produced is called Phoronomics, or “the laws of going”, or more commonly but less properly kinematics [12], to be briefly discussed in section 2.3.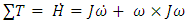
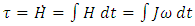
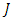 represents the moment of inertia,
represents the moment of inertia, 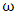 is the angular velocity, and
is the angular velocity, and 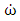 is the angular acceleration. In (2), the angular momentum, defined as H, with its change defined as
is the angular acceleration. In (2), the angular momentum, defined as H, with its change defined as 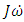 . The additional component
. The additional component 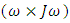 in equation (1) represents the coupled motion of the spacecraft when there is rotation about more than one axis. This coupling creates induced motion about the other axes and is proportional to the mass distribution in the inertia matrix.To derive the angular velocity of the body
in equation (1) represents the coupled motion of the spacecraft when there is rotation about more than one axis. This coupling creates induced motion about the other axes and is proportional to the mass distribution in the inertia matrix.To derive the angular velocity of the body 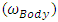 fed from Dynamics to Kinematics, we multiply moment of inertia (J) by the time derivative of angular velocity, i.e., angular acceleration
fed from Dynamics to Kinematics, we multiply moment of inertia (J) by the time derivative of angular velocity, i.e., angular acceleration 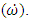 This
This 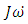 term is multiplied by the inverse of J and then integrated as per equations 2 and 3. Afterwards,
term is multiplied by the inverse of J and then integrated as per equations 2 and 3. Afterwards, 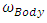 is used to obtain the spacecraft attitude’s Euler Angles.
is used to obtain the spacecraft attitude’s Euler Angles.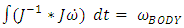
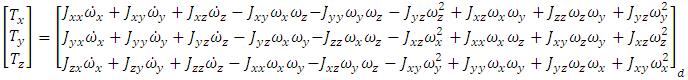

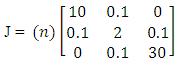
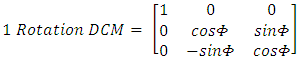
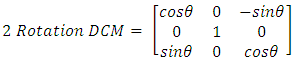
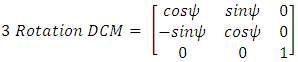
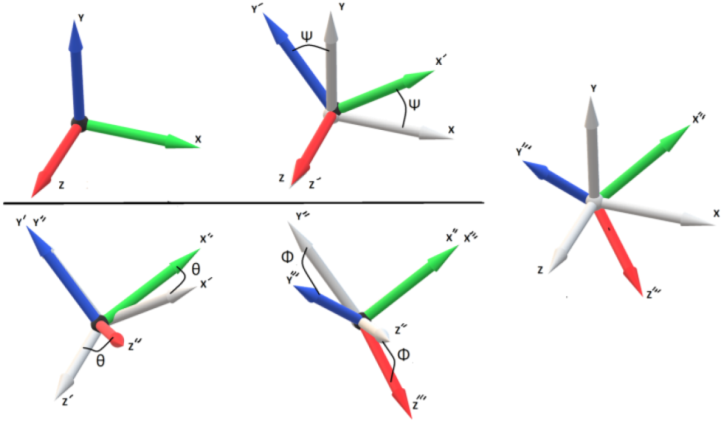
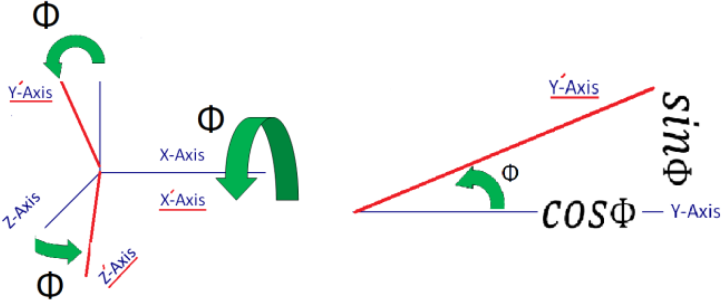
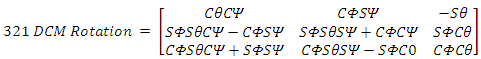
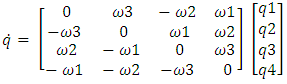
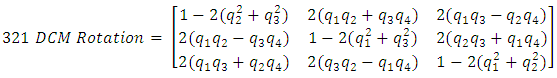
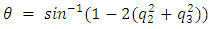
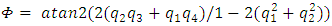
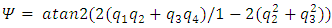
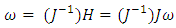
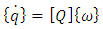
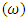 is known, the time invariant solution of the ordinary differential equation in (17), produces a [4x1] dimension quaternion vector (q):
is known, the time invariant solution of the ordinary differential equation in (17), produces a [4x1] dimension quaternion vector (q):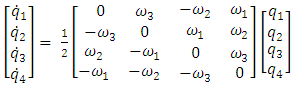
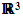 space. The fourth quaternion details the rotation of the Euler axis about itself. A 3-2-1 rotation can be constructed with quaternions using (19):
space. The fourth quaternion details the rotation of the Euler axis about itself. A 3-2-1 rotation can be constructed with quaternions using (19): 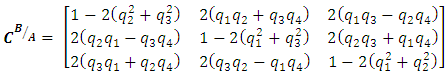
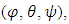 which normally represent rotational movements of pitch, roll and yaw using component rotations (e.g. equations (7), (8), and (9)).
which normally represent rotational movements of pitch, roll and yaw using component rotations (e.g. equations (7), (8), and (9)).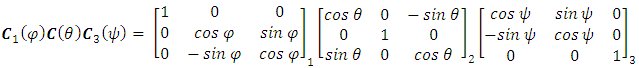
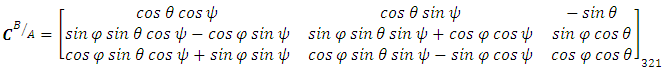
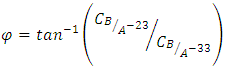
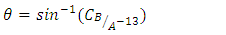
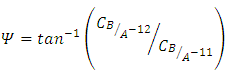
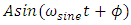
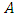 is the amplitude of the maneuver or the desired angular displacement of the spacecraft. The rate at which the spacecraft completes the maneuver is the frequency of the spacecraft denoted as
is the amplitude of the maneuver or the desired angular displacement of the spacecraft. The rate at which the spacecraft completes the maneuver is the frequency of the spacecraft denoted as 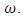 The phase on the sine curve, used to shift the trajectory curve for smooth onset, is denoted by
The phase on the sine curve, used to shift the trajectory curve for smooth onset, is denoted by 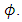 Using the Commanded Euler Angle and the Desired Slew time in conjunction with equation (25), the commanded maneuver is translated into a trajectory using various sine curves. Equation 25 above is expanded into equations (26) through (28) below for investigations of moment of inertia changes in the dynamics, while equation 26 below is used to investigate and compare numerical methods.
Using the Commanded Euler Angle and the Desired Slew time in conjunction with equation (25), the commanded maneuver is translated into a trajectory using various sine curves. Equation 25 above is expanded into equations (26) through (28) below for investigations of moment of inertia changes in the dynamics, while equation 26 below is used to investigate and compare numerical methods. 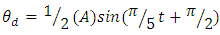
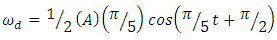
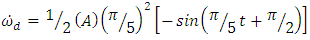
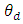 , Angular Velocity
, Angular Velocity 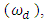 and Angular Acceleration
and Angular Acceleration 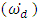 via the MATLAB sine wave function.
via the MATLAB sine wave function.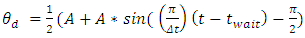
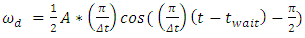
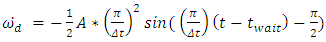
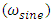 is (π/Δt) where (Δt) is the desired maneuver time. The
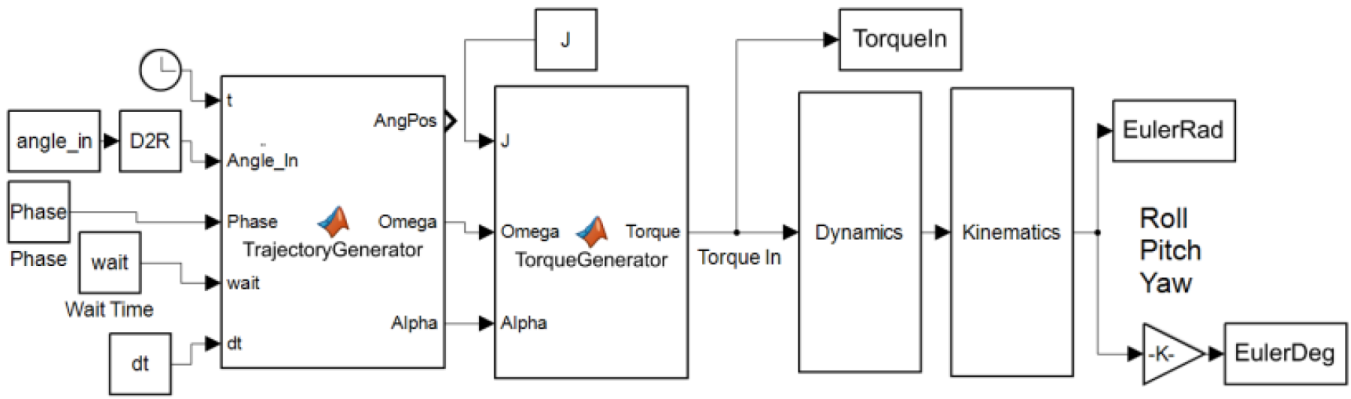
is (π/Δt) where (Δt) is the desired maneuver time. The 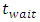 term allows for a quiescent period and -π/2 term allows for a proper phase shift to implement the sinusoidal half period. Equations (30) and (31) are just successive derivatives of equation (29) used to generate angular velocity and acceleration which are fed into the ideal feedforward control equation [46] which resides in the torque generator block of Figure 1. This produces an output torque which drives the dynamics.
term allows for a quiescent period and -π/2 term allows for a proper phase shift to implement the sinusoidal half period. Equations (30) and (31) are just successive derivatives of equation (29) used to generate angular velocity and acceleration which are fed into the ideal feedforward control equation [46] which resides in the torque generator block of Figure 1. This produces an output torque which drives the dynamics. 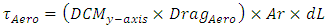
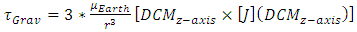
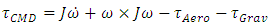
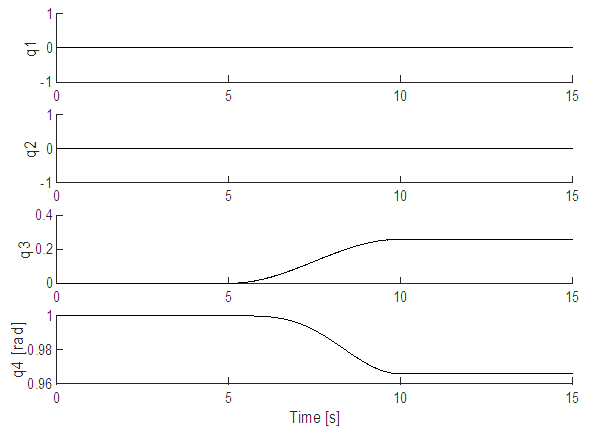
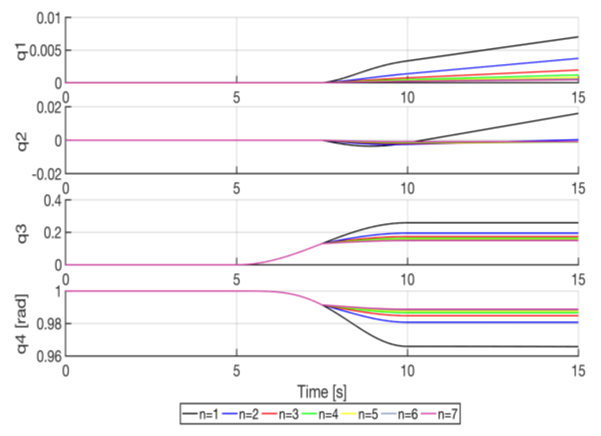
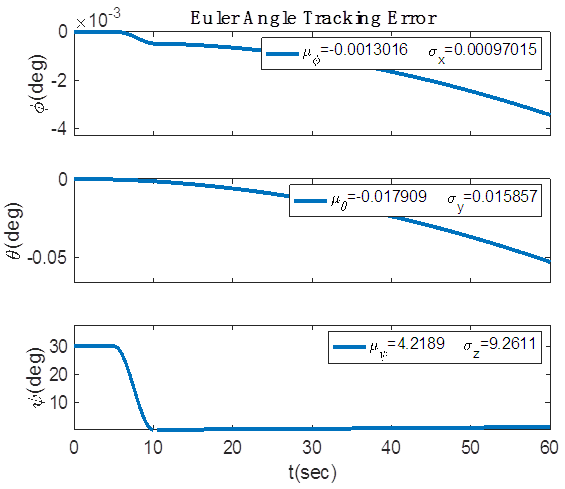
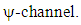 Finer iteration followed the previous investigation of computational efficiency.For the purpose of model verification, commands are initially held constant at zero resulting in zero torque to allow us to evaluate model operation during a quiescent period. With zero input torque, equation (1) shows us that the change in angular momentum should be zero as well; therefore the motion states should not change. After a five second quiescent period, a 30° yaw maneuver was commanded of each model and the maneuver was conducted over a ten second period. Afterwards the output Euler Angles should remain constant with the spacecraft’s new attitude. The results of this test were plotted in Figure 6. Additionally, note that the model was setup with a diagonalized J matrix per equation (5). The roll and pitch Euler Angles remained at zero, as they should have, and as such are not shown.
Finer iteration followed the previous investigation of computational efficiency.For the purpose of model verification, commands are initially held constant at zero resulting in zero torque to allow us to evaluate model operation during a quiescent period. With zero input torque, equation (1) shows us that the change in angular momentum should be zero as well; therefore the motion states should not change. After a five second quiescent period, a 30° yaw maneuver was commanded of each model and the maneuver was conducted over a ten second period. Afterwards the output Euler Angles should remain constant with the spacecraft’s new attitude. The results of this test were plotted in Figure 6. Additionally, note that the model was setup with a diagonalized J matrix per equation (5). The roll and pitch Euler Angles remained at zero, as they should have, and as such are not shown.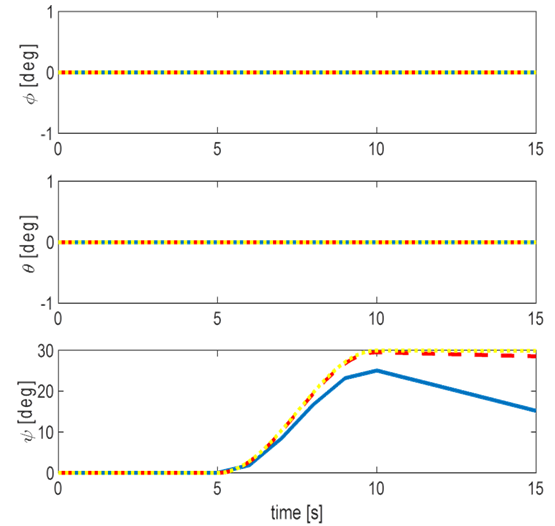
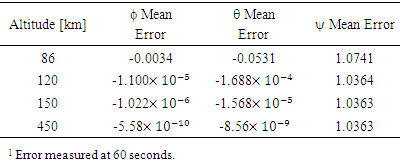
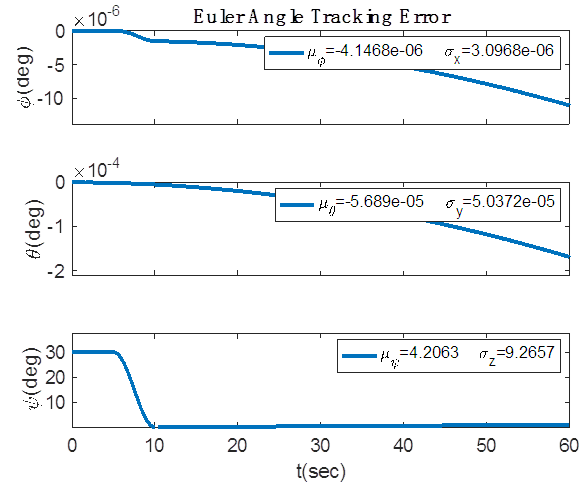
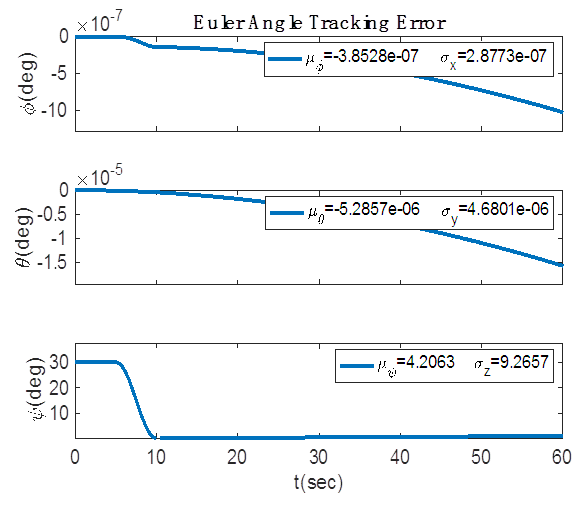
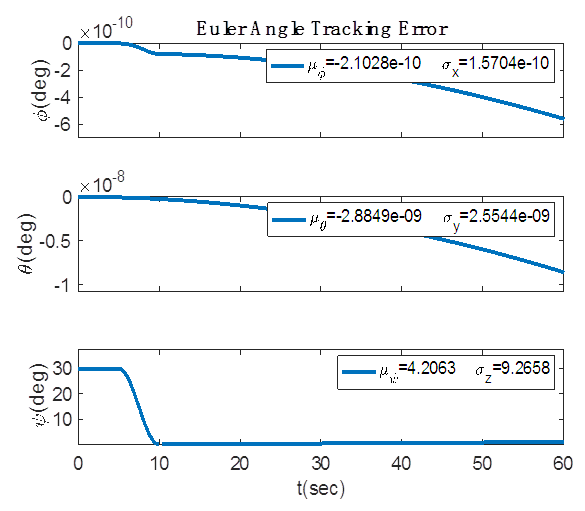
 direction. The maneuver is set up to begin 5 seconds into the simulation and take a total of 5 seconds to complete. Figure (7) shows the four separate altitudes corresponding to Table 1 that the aero torque is tested at and the respective atmospheric densities at those heights. Figures 8-11 shows the differing effect of the aero torque on the movement of the spacecraft corresponding to table 2. The maneuver looks increasingly different as the distance from Earth increases as numerically assessed in Table 2. Table 2 shows the numerical decrease in the effect of the aero torque over an increasing distance. In the
direction. The maneuver is set up to begin 5 seconds into the simulation and take a total of 5 seconds to complete. Figure (7) shows the four separate altitudes corresponding to Table 1 that the aero torque is tested at and the respective atmospheric densities at those heights. Figures 8-11 shows the differing effect of the aero torque on the movement of the spacecraft corresponding to table 2. The maneuver looks increasingly different as the distance from Earth increases as numerically assessed in Table 2. Table 2 shows the numerical decrease in the effect of the aero torque over an increasing distance. In the  channel, the error decreases from 0.0034 to 5.58e-10 over a distance of 364km.
channel, the error decreases from 0.0034 to 5.58e-10 over a distance of 364km.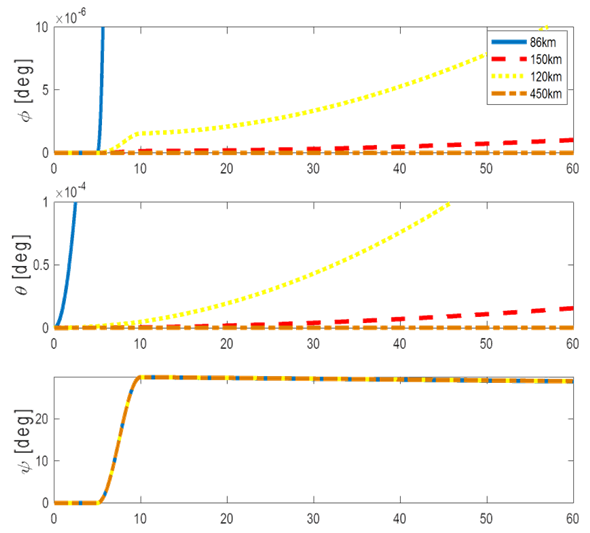
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML