| [1] | C.Z. Xu, J.P. Gauthier and I. Kupka (1993). Exponential stability of the heat exchanger equation. Proc. European Control Conference. 303-307, Groningen, The Netherlands. |
| [2] | C.Z. Xu and G. Weiss (2005). Spectral properties of infinite-dimensional closed-loop systems. Mathematics of Control, Signals and Systems, 17:153-172. |
| [3] | X.D. Li, C.Z. Xu (2009). A further numerical investigation on Luenberger type observers for vibrating systems. 48th IEEE Conference on Decision and Control / Chinese Control Conference World Congress, Shanghai, China, December. |
| [4] | H. Brézis (1973). Opérateurs Maximaux Monotones et Semi-groupes de Contractions dans les Espaces de Hilbert, North Holland, Amsterdam. |
| [5] | H. Brézis (1989). Analyse Fonctionnelle: Théorie et Applications, Masson, Paris. |
| [6] | A. Maidi, M. Diaf et J.P. Corriou (2008a). Optimal linear PI fuzzy controller design of a heat ex hanger. Chemical Engineering and Processing, 47(5), pp 938-945. |
| [7] | A. Maidi, M. Diaf et J.P. Corriou (2008b). Boundary geometric control of a counter-current heat exchanger. Journal of Process Control, In Press. |
| [8] | A. Maidi, J. P. Corriou (2012). Optimal control of nonlinear chemical processes using the variational iteration method. Proc. 8th Symposium on Advanced Control of Chemical Processes, pp. 898-903. |
| [9] | A.V. Wouwer, A., Saucez, P. & Schiesser, W. (2004). Simulation of distributed parameter systems using a Matlab-based method of lines toolbox: chemical engineering applications. Industrial Engineering and Chemistry Research, 43(14): 3469-3477. |
| [10] | L. Torres, C. Verde, A. Villamevh (2018). Global sueprvision system for pipelines using nonlinear redundancy relations. IFAC, Papers OnLine 48-21, pp. 238-243. |
| [11] | A. Rauh, J. Kersten, H. Aschermann (2018). An interval approach for parameter identification and observer design of spatially distributed heating systems. IFAC, Papers OnLine 51-2, pp. 337-342. |
| [12] | F. Zobini, E. Witrant, F. Bonne (2017). PDE observer design of counter-current heat flows in a heat-exchanger. IFAC, Papers OnLine 50-1, pp. 7127-7132. |
| [13] | E. Aulisa, J.A. Nurns, D.S. Gillain (2016). Velocity control of a counter flow heat exchanger. IFAC, Papers OnLine 49-18, pp. 104-109. |
| [14] | E. Kayabasi, H. Kurt (2018). Simulation of heat exchangers and heat exchanger networks with an economic aspect. Eng. Sc. And Tech. An international Journal, 21, pp. 70-76. |
| [15] | A. Hasan, J. Jouffroy (2017). Infinite dimensional boundary observer of Lithium-ion battery state estimation. Energie Procedia 141, pp. 494-501. |
| [16] | M.A. Negret, C. Verde (2012). Multi-leak reconstruction in pipelines by sliding mode observers. Proc of 8th IFAC symposium on fault detection supervision ans safety of technical processes. August 29-31, 2012. Mexico, pp. 934-939. |
| [17] | F Sauvage, D. Dochain, T. Monge (2007). Design of an interval observer for exothermic fed-batch processes. 8th International IFAC symposium on dynamics and control process systems, Proc vol 2, June 4-6, 2007, Mexico, pp. 69-74. |
| [18] | M.S. Barciog, D. Coutinho, A.V. Wouwer (2013). A cascade MPC-feedback linearizing strategy for the multibariable control of animal cells culturs. Proc 9th IFAC symposium on nonlinear control systems. September 4-6, 2013, Toulouse, France. Pp. 247-252. |
| [19] | S. Bourrel, D. Dochain (1998). Adaptative linearizing control of denitrifying biofilter. Proc of IFAC computers applications in biotechnology, Osaka, Japa, 1998. Pp. 547-552. |
| [20] | J. Brown, D. Dochain, M. Perrier, F. Forbes (2002). Modal decomposition of a nonlinear tubular reactor model: a control peerspective. Proc of 15th triennial word congress, Barcelona, Spain, 2002. Pp. 489-494. |
| [21] | O. Tonomura, J. Kans, M. Kano, S. Hasebe (2010). Process monitoring of tubular microreactions using particle filter. Proc of 9th international symposium on dynamics and control of process systems, Leuven, Belgium, July 5-7, pp. 427-432. |
| [22] | I. Torres, I. Queinnec, A.V. Wouwer (2010). Obsevrer based output feedback linearizing control applied to a denitrification reaction. Proc of 11th international symposium on computer application in biotechnology, Leuven, Belgium, July 7-9, 2010. Pp. 102-107. |
| [23] | A. Schaum, J.A. Moreno, J. Alvarez (2008). Dissipativity based globally convergent observer design for a class of tubular reactions. Proc of the 17th world congress, Séoul, Korea, July 6-11, 2008. Pp. 4554-4559. |
| [24] | P.D. Christofides (2001). Nonlinear and robust control of PDE systems: methods and applications to transport-reaction processes. Birkhauser, Boston, 2001. |
| [25] | J. Baker, P. D. Christofides (2000). Finite dimensional approximation and control of non-linear parabolic PDE systems. International Journal of Control, vol. 73, no. 5, pp. 439-456. |
| [26] | S. Skogestad, I. Postlethwaite (2007). Multivariable feedback control: Analysis and Design. Wiley New York, vol. 2. |
| [27] | P.D. Christofides, P. Daoutidis (1997). Finite-dimensional control of parabolic PDE systems using approximate inertial manifolds. Proc of the 36th IEEE Conference on, vol. 2, pp. 1068-1073. |
| [28] | G. G. Rigatos (2015). Control of heat diffusion in arc welding using differential flatness theory and nonlinear Kalman Filtering. IFAC, Papers OnLine, 48-3, pp. 1368-1374. |
| [29] | L. Jadachowski, T. Meurer, A. Kugi (2011). State estimation for parabolic PDEs with varying parameters on 3-Dimensional spatial damains. Proc, 18th world congress the IFAC, Milano (Italy), pp. 13338-13343. |
| [30] | A. Schaum, J. A. Moreno, T. Meurer (2016). Dissipativity-based design for class of coupled 1-D semi-linear parabolic PDES systems. IFAC, Papers OnLine 49-8, pp. 098-103. |
| [31] | T. Kharkovskaia, D. Efinov, A. Palyakov, J. P. Richard (2016). Interval observers for PDE: Approximation approach. IFAC, Papers OnLine, 49-18, pp. 915-920. |
| [32] | S. Afshar, K. Morris, A. Khajepour (2017). State of charge estimation via extended Kalman filter designed for electrochemical equations. IFAC, Papers OnLine 50-1, pp. 2152-2157. |
| [33] | H. Sano (2015). Boundary control of a parallel flow heat exchanger process with boundary observation. IFAC, Papers OnLine 48-1 (2015), pp. 755-760. |
| [34] | H. Sano (2016). Exponential stability of heat exchangers with delayed boundary feedback. IFAC, Papers OnLine 49-8, pp. 043-047. |
| [35] | V. I. Utkin (1993). Sliding mode control design principles and application to electric drivers. IEEE Transactions on Industry Application. Vol 40, n°1, pp 23-36. |


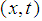 defined on
defined on 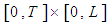 and with values in the real or complex body.The writing of the energy balance for the inner and outer tube of the heat exchanger respectively leads to the following Diffusion-Convection-Reaction partial differential equations:
and with values in the real or complex body.The writing of the energy balance for the inner and outer tube of the heat exchanger respectively leads to the following Diffusion-Convection-Reaction partial differential equations: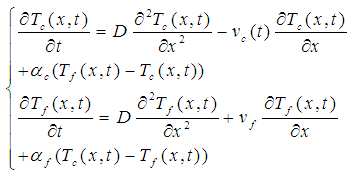
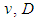 and
and 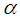 represent the flow velocity of the fluid
represent the flow velocity of the fluid 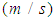 , the diffusion coefficient
, the diffusion coefficient 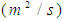 and the heat transfer coefficient, respectively. The indices f and c respectively symbolize the cold and the hot.[6], [7] and recently [13], have explained that diffusion phenomena are frequently neglected (
and the heat transfer coefficient, respectively. The indices f and c respectively symbolize the cold and the hot.[6], [7] and recently [13], have explained that diffusion phenomena are frequently neglected (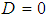 ) in heat exchangers. This hypothesis reduces the model of the heat exchanger (1) to a Convection-Reaction type model:
) in heat exchangers. This hypothesis reduces the model of the heat exchanger (1) to a Convection-Reaction type model: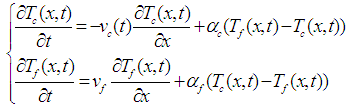
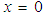 for the hot fluid and
for the hot fluid and 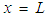 for the cold fluid (L is length of the exchanger), the boundary conditions of Dirichlet:
for the cold fluid (L is length of the exchanger), the boundary conditions of Dirichlet: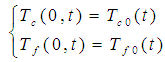
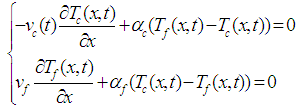
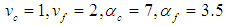 • Boundary conditions for hot fluid
• Boundary conditions for hot fluid 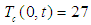 • Boundary conditions for cold fluid
• Boundary conditions for cold fluid 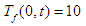 • The number of discretization point
• The number of discretization point 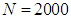 ,• The step of discretization :
,• The step of discretization : 
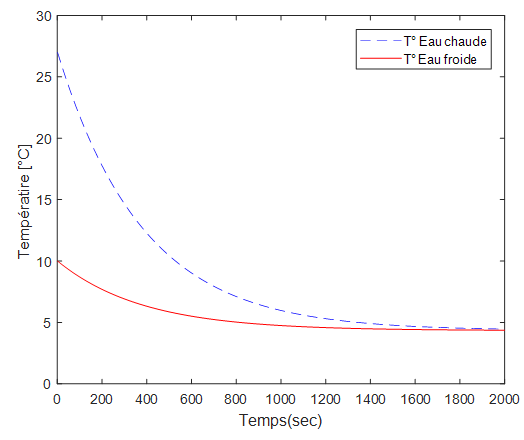
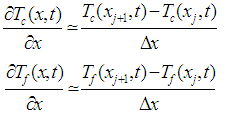 The system of ordinary differential equation (EDO) obtained by applying the method of the lines, is solved by using solver ode45 of MATLAB.Figure 2 shows the spatial-temporal profiles of the temperatures of each fluid in the heat exchanger system.
The system of ordinary differential equation (EDO) obtained by applying the method of the lines, is solved by using solver ode45 of MATLAB.Figure 2 shows the spatial-temporal profiles of the temperatures of each fluid in the heat exchanger system.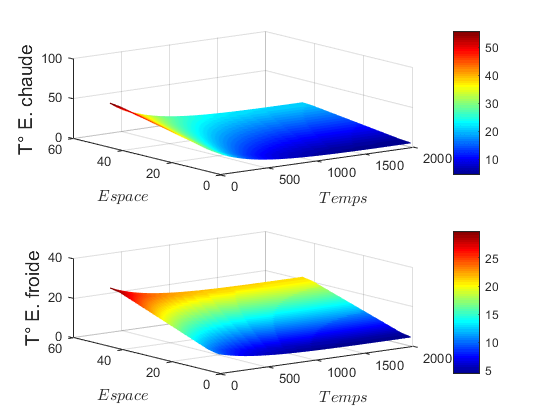
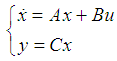
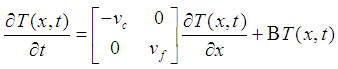
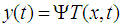
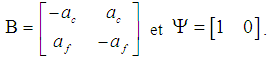
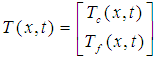 Represents the state of the system.The operator
Represents the state of the system.The operator 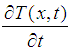 et
et 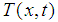 belong to the Hilbert space defined as follows:
belong to the Hilbert space defined as follows: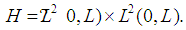 For each
For each 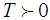 , we define a linear application:
, we define a linear application: 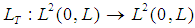 , which associates the output y with each input
, which associates the output y with each input 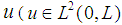 ).
). 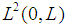 is the space of measurable functions in the real and integrable square body.In this canonical form of equation, Kalman filters and Luenberger observers were synthesized to estimate unmeasured states [21], [32], [23], [18] and more recently [12]. This literature also shows that the observability of SPD systems is linked to the choice of sensors and their locations.The originality of our contribution consists into the synthesis of a sliding mode observer ([35], [12]) in infinite dimension. As with any observer, it is based on the model of the system.Thus for the tubular heat exchanger represented by the EDP system (2), the sliding mode observer is given by the following equation system:
is the space of measurable functions in the real and integrable square body.In this canonical form of equation, Kalman filters and Luenberger observers were synthesized to estimate unmeasured states [21], [32], [23], [18] and more recently [12]. This literature also shows that the observability of SPD systems is linked to the choice of sensors and their locations.The originality of our contribution consists into the synthesis of a sliding mode observer ([35], [12]) in infinite dimension. As with any observer, it is based on the model of the system.Thus for the tubular heat exchanger represented by the EDP system (2), the sliding mode observer is given by the following equation system: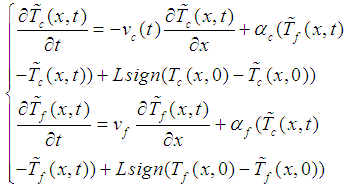
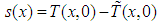 represents the sliding surface.The term
represents the sliding surface.The term 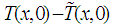 assumes that the state of the system is not measurable everywhere.
assumes that the state of the system is not measurable everywhere.
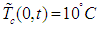 and
and 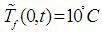 .L is chosen equal to 500. This value is used in a way that its multiplication with the time discretization step is approximately equal to the dynamics of the gaps between successive measured values. The observer was implemented by considering a finite difference approximation before differential operators, with a spatial pitch
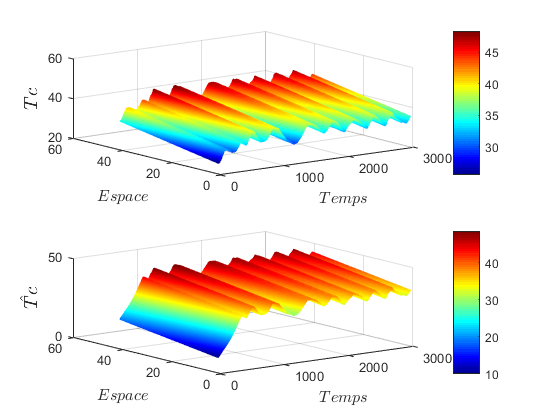
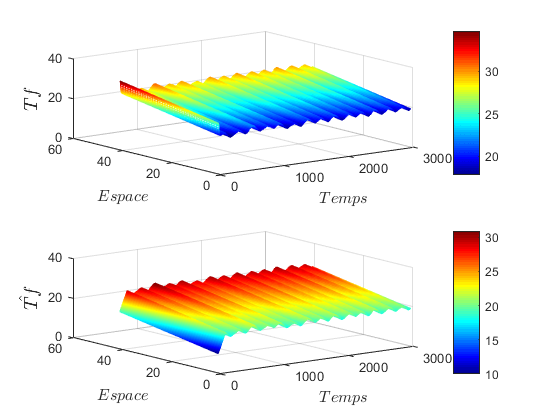
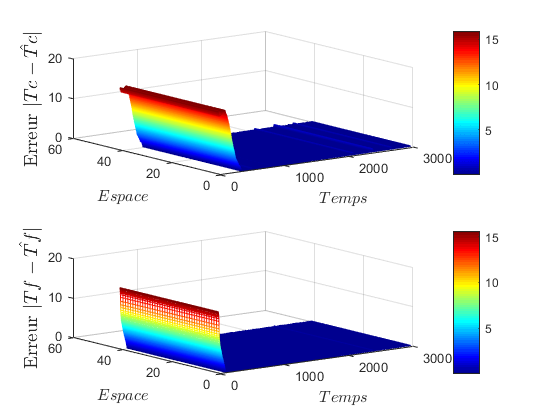
.L is chosen equal to 500. This value is used in a way that its multiplication with the time discretization step is approximately equal to the dynamics of the gaps between successive measured values. The observer was implemented by considering a finite difference approximation before differential operators, with a spatial pitch 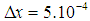 .The results of the sliding mode observer for hot and cold fluid are shown in Figure 4.
.The results of the sliding mode observer for hot and cold fluid are shown in Figure 4.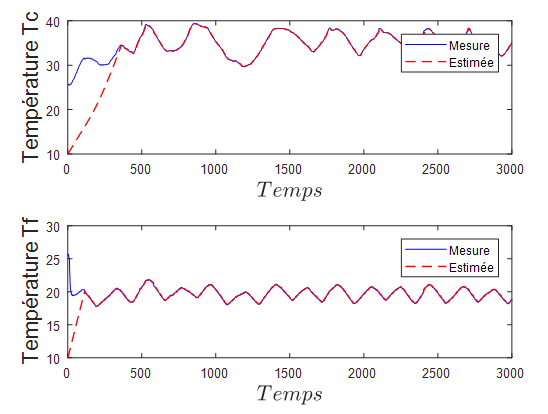
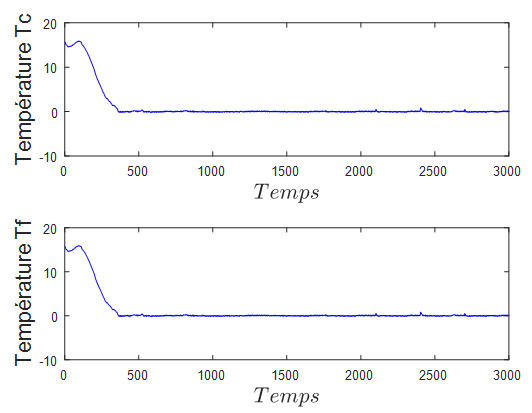
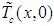 and
and 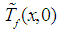 converge quickly to
converge quickly to 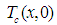 and
and 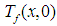 respectively, even if they are different at the beginning. This difference is due to the initialization of the boundary conditions of the observer.To furthermore accelerate the convergence of the observer, we can increase the value of the gain of the latter. With this, the Figure 6 shows the dynamics of the observation system and the observer, for a value of the gain L = 600. It should also be noted in this figure that the increase of the speed of convergence degrades the stability of the observer. In the end, everything is about a compromise speed-stability.
respectively, even if they are different at the beginning. This difference is due to the initialization of the boundary conditions of the observer.To furthermore accelerate the convergence of the observer, we can increase the value of the gain of the latter. With this, the Figure 6 shows the dynamics of the observation system and the observer, for a value of the gain L = 600. It should also be noted in this figure that the increase of the speed of convergence degrades the stability of the observer. In the end, everything is about a compromise speed-stability.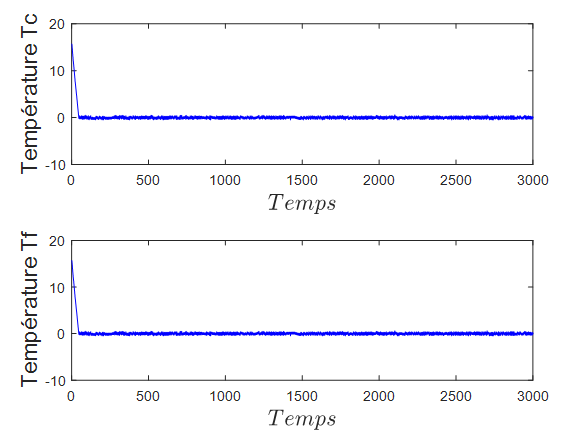
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML