-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2017; 7(1): 11-17
doi:10.5923/j.control.20170701.02

Optimal Scheduling and Control of High Throughput Screening Systems using Max-plus Linear Systems
Ying Shang, Adetola Oke
Department of Electrical and Computer Engineering, Southern Illinois University Edwardsville, Edwardsville, USA
Correspondence to: Ying Shang, Department of Electrical and Computer Engineering, Southern Illinois University Edwardsville, Edwardsville, USA.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper presents a prefilter solution to the model reference control in high throughput screening in drug discovery, an automatic compound screening and analyzing process in pharmaceutical industries. Such a prefilter will generate an optimal scheduling despites of the system malfunctions and delays. The approach used in this paper is the max-plus linear system modelling and control in discrete-event systems. The main results are illustrated using enzyme screening compound screening applications.
Keywords: High-throughput screening systems, Discrete-event systems, Max-plus linear systems
Cite this paper: Ying Shang, Adetola Oke, Optimal Scheduling and Control of High Throughput Screening Systems using Max-plus Linear Systems, International Journal of Control Science and Engineering, Vol. 7 No. 1, 2017, pp. 11-17. doi: 10.5923/j.control.20170701.02.
Article Outline
1. Introduction
- A successful drug discovery is an extremely time-consuming procedure, including initial target identification and validation, pre-clinical trials on animals, regulatory approval to start trials in humans, clinical trials, submission of marketing and manufacturing authorization, licensing review, product on sale, and post-marketing surveillance [11, 13, 14, 16, 21]. Figure 1 illustrates a flow chart of a typical drug discovery process. After target identification and validation, researchers in biology, biochemistry, and pharmaceutical science test diverse chemical compounds in order to find hits, which are compounds with desired effects on targets. With the development of robotics and high-speed computing technology, it is feasible to develop automatic systems that can screen a large number of biochemical compounds in a short period of time. Such an automatic compound screening and analyzing process is called high-throughput screening (HTS) in drug discovery of pharmaceutical industries. HTS provides a practical and efficient method to test a large number of synthetic compounds in miniaturized in vitro assays to identify hit targets of interest. Then, the chemical compounds that have therapeutic and useful pharmacological or biological activities, called leads, are evaluated and undergo lead optimization to identify promising lead compounds. Followed by the initial synthesis and animal testing in preclinical trials and three phases of clinical trials on humans, a drug can be put on market after the Food and Drug Administration (FDA) approval.
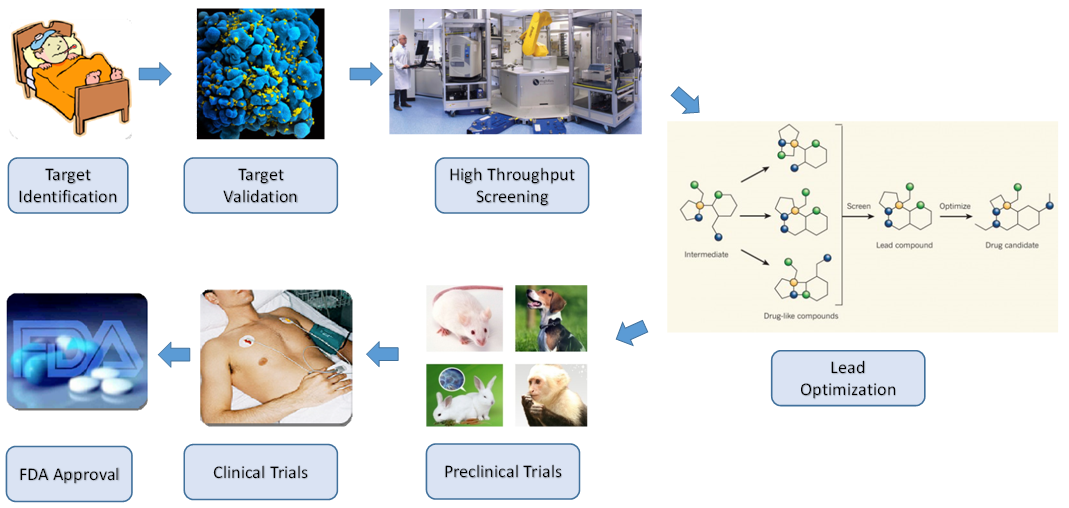 | Figure 1. Drug discovery process flowchart |
2. Literature Review
- The optimal scheduling of testing a large number of compounds requires innovative modeling, advanced scheduling algorithms, effective communication tools, and friendly user interfaces. However, the HTS scheduling is far more challenging than traditional scheduling in chemical or manufacturing engineering in the following aspects: (1) each batch may pass the same machine more than once; (2) more than one batch may be present in an HTS system at the same time; (3) there are no buffers between machines; (4) a batch may occupy multiple machines simultaneously; (5) there are upper time bounds, i.e. due dates for processes, or time window constraints because of process requirements; (6) operating schemes are strictly cyclic, meaning that the distance between two consecutive chemical batches is always constant. Due to these challenging factors, the optimal scheduling of HTS systems has been known as an “np-hard” problem and has not been thoroughly studied. The origin, evolution, current state of arts, challenges, and future opportunities for HTS systems can be found in [11, 13, 14, 16, 21]. From 1980 to 2011, the speed of HTS has increased from 10-100 compounds per week to 8000 tests per day. Drug discovery requires HTS processes have higher quality, higher cost-efficiency, and higher throughput in compound testing in order to reduce the number of false diagnostics, such as false positives and false negatives, and increase the number of compounds tested within a certain time. In this proposal, I investigate the highly automated HTS processes in drug discovery to identify the optimal scheduling for testing compounds. The expected outcome of this project will reduce compound waste, help produce consistent compound mixtures, and increase the number and quality of hits in the testing. A better scheduling algorithm and a better automation control paradigm proposed in this project target three key challenges in HTS systems: time, costs, and quality [13]. Time can be reduced by a more efficient, robust, and accurate scheduling algorithm resulting in less delay, fewer compound waste, and better assay adaptations. The optimal scheduling can reduce the cost of automation, personnel, consumables, and reagents in HTS systems. Moreover, the quality of the screening will be improved as a consequence of the improvement of the process efficiency.Scheduling of testing almost an unlimited number of compounds in an HTS system belongs to a general class of cyclic scheduling problems [9]. Except for special cases, cyclic scheduling problems are np-hard, in other words, that the computational complexity of the scheduling problems is exponentially increasing with respect to the size of the systems. Previous research developed globally optimal solutions for scheduling in HTS systems using mixed integer linear programming (MIP) models [13]. There are several drawbacks of these MIP models. First, they are inefficient and require a substantial amount of time to compute an optimal solution for even a small size scheduling problem. This has limited their applications to only trivial problems and available MIP models cannot be used for real-time scheduling of HTS systems. Secondly, existing HTS scheduling methods do not employ any algorithms that take advantage the properties of HTS scheduling and improve computation efficiency. For example, available MIP models for HTS systems use optimization software packages (e.g., CPLEX) to find the optimal scheduling. Thirdly, none of the existing HTS scheduling methods has been tested on real-world HTS systems. This research paper provides an efficient HTS scheduling model using discrete-event systems and validate it using real-world HTS systems. The scheduling in HTS systems is typically implemented by computer software embedded in the HTS robots [15]. A globally optimal scheduling method based on discrete-event system modeling was developed for cyclic HTS systems [12]. Discrete-event systems are event-driven systems where the state evolutions depend on the occurrences of asynchronous discrete events over time. Such cyclic scheduling is called overtaking [17] or interleaving [15]. Using the predetermined static schedule, an algebraic model of the HTS system's activities was established [4, 5]. Because static schedules do not perform well when deviations occur during run-time [15], a feedback controller is designed to generate an optimal just-in-time schedule at the presence of unexpected deviations from the cyclic scheme. To summarize, the existing online scheduling algorithms [15] do not perform well where malfunctions are present. The predetermined static schedules [4, 5, 12] require the schedules to be known in advance. This project integrates and adapts the algebraic modeling for HTS systems [4, 5] and advanced scheduling algorithms in manufacturing, and develops an innovative optimal scheduling and control strategy for HTS systems.
3. Max-plus Linear System Modeling
- Discrete-event systems, which have been used to model communication networks, manufacturing systems, and transportation infrastructures, are used to mode HTS systems [12]. A special algebraic structure, Max-plus algebra [4, 5], is used for offline optimal scheduling and control synthesis. This proposal adopts the discrete-event system modeling approach because it provides a systematic method for modeling and controller synthesis for HTS systems. A very simple HTS system is shown Figure 2, where the robot deposits the chemical compounds in a microplate, which takes 5 seconds. Then the robot takes the microplate and drops off the microplate in the incubator, which takes another 2 seconds.
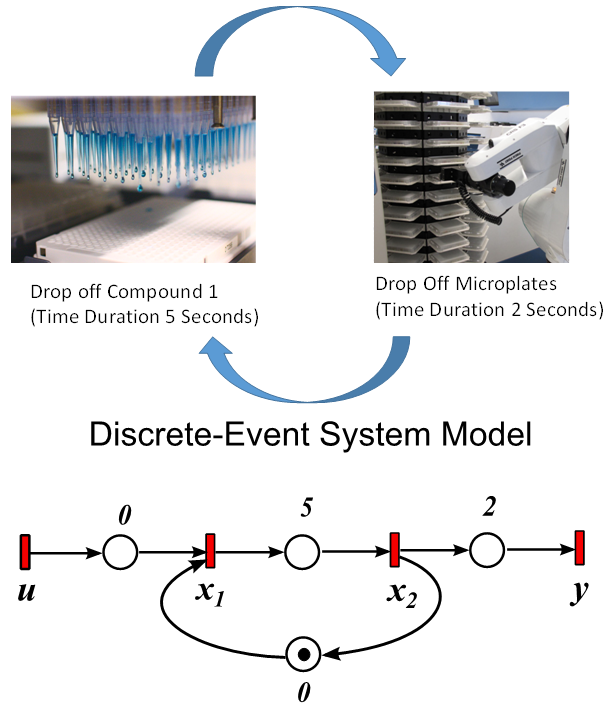 | Figure 2. An example of transporting a microplate to the incubator for an HTS system (top) and its corresponding discrete-event system model (bottom) |
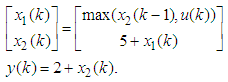 | (1) |
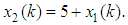 The output equation implies that the robot takes 2 time units to move the microplate to the incubator after the k-th compound was dropped (x2(k)).Typically, discrete-event systems are very complex, nonlinear, and hierarchical and often have synchronization behaviors in the occurrences of the events. The max-plus linear systems [1] are used to describe timed discrete-event systems by incorporating the traditional linear system theory in modeling and analysis of nonlinear synchronization behaviors in event-driven systems. This simple HTS example is used to illustrate the main advantage of max-plus linear system modeling for discrete-event systems, which is the adoption of the traditional linear system schematics (Eq. (1)), where
The output equation implies that the robot takes 2 time units to move the microplate to the incubator after the k-th compound was dropped (x2(k)).Typically, discrete-event systems are very complex, nonlinear, and hierarchical and often have synchronization behaviors in the occurrences of the events. The max-plus linear systems [1] are used to describe timed discrete-event systems by incorporating the traditional linear system theory in modeling and analysis of nonlinear synchronization behaviors in event-driven systems. This simple HTS example is used to illustrate the main advantage of max-plus linear system modeling for discrete-event systems, which is the adoption of the traditional linear system schematics (Eq. (1)), where 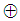 denotes the max-operation,
denotes the max-operation, 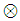 denotes the addition:
denotes the addition: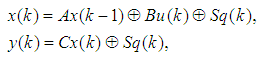 | (2) |
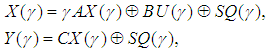 | (3) |
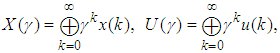
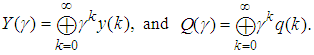
4. Optimal Scheduling and Controller Design for HTS Systems using Max-Plus Linear Systems
- If we have an enzyme compound screening, the microplates contain compounds, enzyme solution gets manually added during the barcode reader 1 min incubation, and then enzyme substrate is added by a multidrop dispenser, which is an automatic, programmable dispenser for micro volume dispensing. Then, this is followed by an incubation period or the reaction and then reading the plate on the envision, as a measure of the enzyme reaction. Time constraint would be most critical for the substrate addition, incubation and readout process to ensure that the readout is obtained in the linear range and in a consistent manner for all plates (9 minutes of incubation all the time). Time constraints may also be put in place to avoid the plate sitting without a lid for extended periods of time (so any evaporation is limited). The HTS system can be modelled as a special discrete-event systems, called a “timed-event graph” (TEG), which is a special discrete-event model with on one upstream and one downstream transition, respectively. Figure 3 illustrates the HTS workflow for the enzyme compound screening.The corresponding variables are defined in Table 1. Figure 3 is a simplified time-event graph from a 35-transition state machine initially for easier understanding of the readers. The control signal is the time instant that the user starts to the k-th screening of the compound. Between robot picking up the microplate in the incubator, x1 and robot dropping off the microplate in the incubator, x2, the time duration of 221 seconds include the picking up the microplate, removing the lid, changing the grip position, move to the barcode reader, etc. Once the microplate is in the incubator already, it is required to stay in the incubator for 9 minutes, no more and no less ideally for consistency in order to avoid contamination and compound reactions. The k+1-th microplate can be picked up after the k-th microplate is in the incubator, which is represented by the transition from x2 to x1, with one place with one token. The k-th microplate cannot be picked up after 9 minute (540 seconds) of incubation before before the k-1-th microplate is back in the incubator, which is represented by the transition from x4 to x3, with one place with one token. The disturbances marked in red transitions represent all the possible malfunctions and delays during this process. The transition from x3 to x1 with -761 seconds are the time constraints to guarantee the incubation time is no longer than 9 minutes (540 seconds), i.e. x1+221+540<x3.
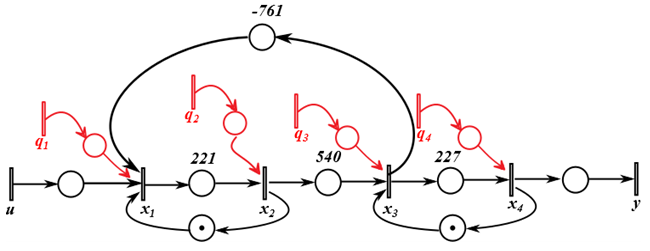 | Figure 3. HTS workflow for the enzyme screening |
|
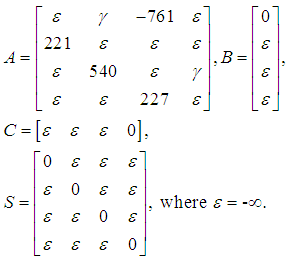 The system equation in Eq. (3) can be rewritten as follows by solving the implicit equation (3):
The system equation in Eq. (3) can be rewritten as follows by solving the implicit equation (3):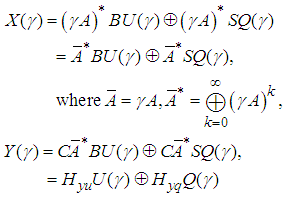 | (4) |
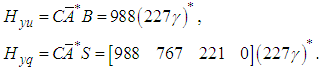 The state and output series represent the time instants of the k-th screening. If the screening needs to meet certain standards with respect to the speed, cost, and throughput, for instant, denoted as the reference transfer function Gref, see Figure 4. We can design an open-loop profiler controller such that Gref=HP, where H can be Hyu or Gref can be Hyq, if one wants to minimize the cycle time or maximize the throughput despites of disturbances, assuming some degrees of measurement with disturbances.
The state and output series represent the time instants of the k-th screening. If the screening needs to meet certain standards with respect to the speed, cost, and throughput, for instant, denoted as the reference transfer function Gref, see Figure 4. We can design an open-loop profiler controller such that Gref=HP, where H can be Hyu or Gref can be Hyq, if one wants to minimize the cycle time or maximize the throughput despites of disturbances, assuming some degrees of measurement with disturbances.  | Figure 4. Model reference control in max-plus systems [19] |
4.1. Disturbance Decoupling
- The optimal solution for the prefilter can be calculated by the left and right residuation defined as follows, respectively:
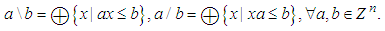 Therefore, the optimal prefilter is obtained by the following argument for any disturbances:
Therefore, the optimal prefilter is obtained by the following argument for any disturbances: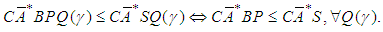 Then, the optimal prefilter solving the model reference control is
Then, the optimal prefilter solving the model reference control is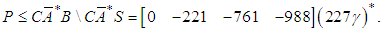 Notice that P is not causal, we can obtain the causal projection by remov ing the negative time instants, i.e.
Notice that P is not causal, we can obtain the causal projection by remov ing the negative time instants, i.e. 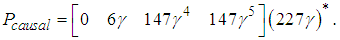 The causal prefilter can be realized through the time-event graph shown in Figure 5. The cyclic place with one token and 227 second time delay presents (227γ)*, each element represent how to generate the control u from the disturbances. For instance, from q1 to v, there is an empty place with no delay and no token, which is Pcausal(1,1); from q3 to v, there is a place with one token and 6 seconds time delay, which is Pcausal(1,2); from q2 to v, there is a place with four tokens and 6 second time delay, which is Pcausal(1,3); and from q4 to v, there is a place with five tokens and 147 seconds time delay, which is Pcausal(1,4). The optimal scheduling generated by the residuation is given as below:
The causal prefilter can be realized through the time-event graph shown in Figure 5. The cyclic place with one token and 227 second time delay presents (227γ)*, each element represent how to generate the control u from the disturbances. For instance, from q1 to v, there is an empty place with no delay and no token, which is Pcausal(1,1); from q3 to v, there is a place with one token and 6 seconds time delay, which is Pcausal(1,2); from q2 to v, there is a place with four tokens and 6 second time delay, which is Pcausal(1,3); and from q4 to v, there is a place with five tokens and 147 seconds time delay, which is Pcausal(1,4). The optimal scheduling generated by the residuation is given as below: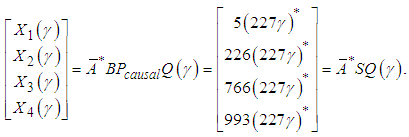 Where the disturbance Q(γ) is 5 second delay of the operation due to malfunction on x1. If the system runs autonomously without disturbances, the scheduling is the following:
Where the disturbance Q(γ) is 5 second delay of the operation due to malfunction on x1. If the system runs autonomously without disturbances, the scheduling is the following: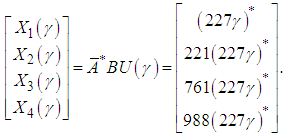 You may observe for every transition, it is exactly 5 second delay of the operation. Therefore, the prefilter Pcausal provides the optimal scheduling such that the system will start running right away after the malfunction is cleared without further delay based on the just-in-time criterion.
You may observe for every transition, it is exactly 5 second delay of the operation. Therefore, the prefilter Pcausal provides the optimal scheduling such that the system will start running right away after the malfunction is cleared without further delay based on the just-in-time criterion. 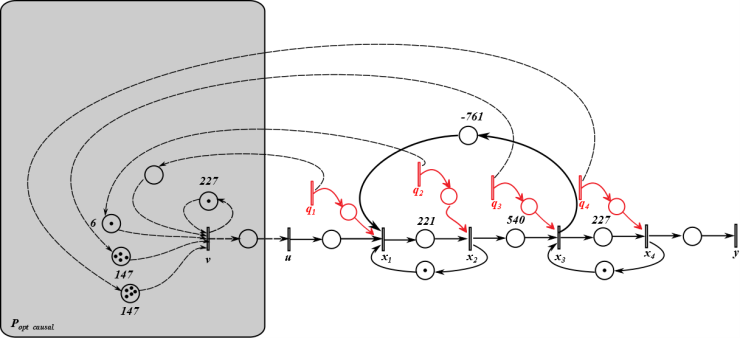 | Figure 5. Timed-event graph model for the HTS system with prefilter |
5. Conclusions
- Discrete-event systems are event-driven systems where the state evolutions depend on the occurrences of asynchronous discrete events over time. Max-plus linear systems are used to model a special discrete event systems with up to one upward transition and up to one downward transition. The advantage of the max-plus linear systems is modelling the synchronization and nonlinearity of discrete event systems in a linear manner, especially the optimal scheduling problem in discrete event systems. This paper used the max-plus linear system modelling to find a prefilter solution to the model reference control in high throughput screening in drug discovery. Such a prefilter will generate an optimal scheduling despites of the system malfunctions and delays. The main results are illustrated using enzyme screening compound screening applications. In fact, state feedback and output feedback can also be designed for such system to achieve optimal scheduling. Moreover, industrial standard scheduling algorithms can be used to high-throughput screening systems as well.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML