-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2017; 7(1): 1-10
doi:10.5923/j.control.20170701.01

Separation Principle for a Class of Takagi-Sugeno Descriptor Models
Ilham Hmaiddouch1, 2, El Mahfoud El Bouatmani1, 2, Jalal Soulami1, 2, Abdellatif El Assoudi1, 2, El Hassane El Yaagoubi1, 2
1Laboratory of High Energy Physics and Condensed Matter, Faculty of Science, Hassan II University of Casablanca, Casablanca, Morocco
2ECPI, Department of Electrical Engineering, ENSEM, Hassan II University of Casablanca, Casablanca, Morocco
Correspondence to: Jalal Soulami, Laboratory of High Energy Physics and Condensed Matter, Faculty of Science, Hassan II University of Casablanca, Casablanca, Morocco.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper studies the design problem of an observer-based controller for a class of nonlinear descriptor systems described by Takagi-Sugeno (T-S) fuzzy structure [1, 2] where the premise variables are unmeasurable. Based on the combination of the control law established in [3] and the fuzzy observer in explicit structure given in [4], a new procedure to investigate the separation principle problem for the considered class of Takagi-Sugeno descriptor models (TSDMs) is then proposed. The guarantee of the global asymptotic stability of the closed-loop augmented system is proved by using the Lyapunov theory and the conditions of asymptotic stability are given in terms of linear matrix inequalities (LMIs). Finally, an application based on rolling disc process is presented as an illustrative example to show the performance of the proposed dynamic controller design.
Keywords: Takagi-Sugeno descriptor model, Fuzzy observer, State feedback controller, Lyapunov method, LMI technique, Separation principle
Cite this paper: Ilham Hmaiddouch, El Mahfoud El Bouatmani, Jalal Soulami, Abdellatif El Assoudi, El Hassane El Yaagoubi, Separation Principle for a Class of Takagi-Sugeno Descriptor Models, International Journal of Control Science and Engineering, Vol. 7 No. 1, 2017, pp. 1-10. doi: 10.5923/j.control.20170701.01.
Article Outline
1. Introduction
- It is well-known that in order to realize in practice a stabilisation by static state feedback for most industrial applications, the separation principle variously called dynamic output feedback controller or observer-based controller plays a key role since instead of a full-state feedback, we use signals reconstructed by a state observer from the on-line measurements of the input and output of the process. The aim of the paper consists to design an observer-based controller for a class of nonlinear descriptor systems described by T-S representation. Notice that, descriptor models representation has been widely used in the dynamic modeling of many chemical and physical processes [5-8]. The numerical simulation of such dynamic models usually combines an ODE numerical method together with an optimization algorithm. In the literature, there have been several studies concerning the issue of stability and the stabilisation of T-S models [9-11]. Likewise, many works have been carried out to investigate the observer design of T-S models [12-15]. The separation property of T-S observers and controllers was discussed by [16-20]. For TSDMs which are defined by extending the ordinary T-S representation [3, 21], several research works concerning the problem of control and observation design and applications have been developed [3, 4, 21-25]. Notice that, generally an interesting way to solve the various fuzzy observer and controller problems raised previously is to write the convergence conditions on the LMI form [26].Based on the use of the state feedback given in [3] and the fuzzy observer proposed in [4], the main contribution of this paper consists to propose a new result of separation principle for a class of TSDMs with unmeasurable premise variables. The global asymptotic stability of the closed-loop system is studied by using the Lyapunov theory and the stability conditions are given in terms of LMIs. Moreover, the proposed result is given without the use of an optimization algorithm.The outline of the paper is structured as follows. In Section 2, the considered class of TSDMs with unmeasurable premise variables is presented. In Section 3, the main result about fuzzy observer-based controller design is established. The control and observer gains are found directly from LMI formulation. Finally, in Section 4, an illustrative application to show the good performance of the proposed result is given.Throughout the paper, some notations used are fair standard. For example,
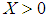 means the matrix
means the matrix 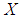 is symmetric and positive definite.
is symmetric and positive definite. 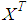 denotes the transpose of
denotes the transpose of 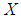 . The symbol I (or 0) represents the identity matrix (or zero matrix) with appropriate dimension.
. The symbol I (or 0) represents the identity matrix (or zero matrix) with appropriate dimension. 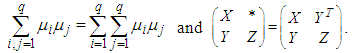 At first, we recall some basic lemmas that are frequently used in the setting the proof of the main result of this paper.Lemma 1 (Congruence): Let two matrices
At first, we recall some basic lemmas that are frequently used in the setting the proof of the main result of this paper.Lemma 1 (Congruence): Let two matrices  and
and  , if
, if 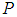 is positive definite and if
is positive definite and if 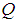 is a full column rank matrix, then the matrix
is a full column rank matrix, then the matrix 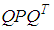 is positive definite.Lemma 2 (Young's inequality): For any matrices
is positive definite.Lemma 2 (Young's inequality): For any matrices 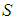 and
and 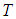 with appropriate dimensions, the following property holds for any invertible matrix
with appropriate dimensions, the following property holds for any invertible matrix 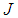 and scalar
and scalar  :
: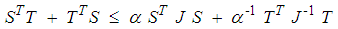 | (1) |
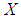 ,
, 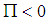 and a scalar
and a scalar 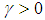 , the following holds:
, the following holds: 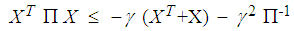 | (2) |
2. Takagi-Sugeno Descriptor Models
- The following class of TSDMs is considered in this paper:
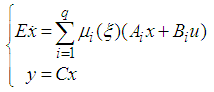 | (3) |
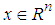 is the state vector,
is the state vector, 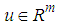 is the control input,
is the control input, 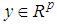 is the measured output.
is the measured output. 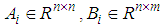 ,
, 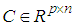 and
and 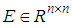 such that
such that 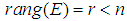 , are real known constant matrices.
, are real known constant matrices. 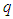 is the number of sub-models.
is the number of sub-models. 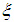 is the premise variable which can be here depend on completely or partially unmeasured state of the system and the
is the premise variable which can be here depend on completely or partially unmeasured state of the system and the 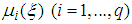 are the weighting functions that ensure the transition between the contribution of each sub model:
are the weighting functions that ensure the transition between the contribution of each sub model: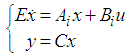 | (4) |
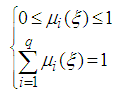 | (5) |
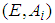 is regular, i.e.
is regular, i.e. 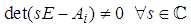 H2) Sub-models (4) are impulse controllable and stabilisable.H3) Sub-models (4) are impulse observable and detectable.Moreover, the following hypothesis which is necessary for the observer design given in [4] is assumed to be verified:H4)
H2) Sub-models (4) are impulse controllable and stabilisable.H3) Sub-models (4) are impulse observable and detectable.Moreover, the following hypothesis which is necessary for the observer design given in [4] is assumed to be verified:H4) 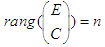 Note that from the consideration of the hypothesis H4), there exists a non-singular matrix
Note that from the consideration of the hypothesis H4), there exists a non-singular matrix  such that:
such that: 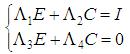 | (6) |
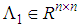 ,
, 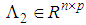 ,
, 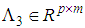 ,
, 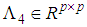 are constant matrices which can be found by the singular value decomposition of
are constant matrices which can be found by the singular value decomposition of 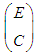 .In order to investigate the separation principle problem for the considered class of TSDMs (3), firstly the following control law established in [3] is adopted:
.In order to investigate the separation principle problem for the considered class of TSDMs (3), firstly the following control law established in [3] is adopted: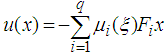 | (7) |
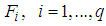 can determined in order that the closed-loop system (3) is asymptotically stable. The following result has been studied in [3].Theorem 1 [3]: The closed-loop system (3)-(7) is globally exponentially stable if there exist matrices
can determined in order that the closed-loop system (3) is asymptotically stable. The following result has been studied in [3].Theorem 1 [3]: The closed-loop system (3)-(7) is globally exponentially stable if there exist matrices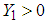 ,
, 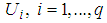 verifying the following LMIs:
verifying the following LMIs: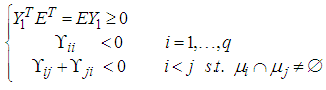 | (8) |
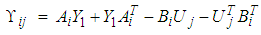 | (9) |
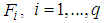 are given by:
are given by: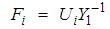 | (10) |
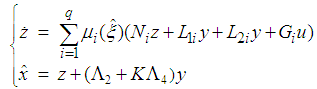 | (11) |
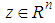 is the state of fuzzy observer and
is the state of fuzzy observer and 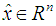 is the estimate of
is the estimate of 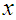 .
. 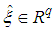 denotes the estimated premise variables vector. The matrices
denotes the estimated premise variables vector. The matrices 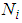 ,
, 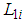 ,
, 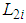 ,
, 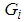 and
and 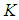 are unknown matrices of appropriate dimensions to be determined such that
are unknown matrices of appropriate dimensions to be determined such that 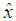 converges asymptotically to
converges asymptotically to 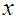 .
. 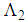 and
and 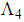 are such that equation (6) is satisfied.The convergence condition of the observer (11) can be formulated by the following Theorem.Theorem 2 [4]: The state error between the T-S descriptor model (3) and its observer (11) converges asymptotically towards zero, if there exist matrices
are such that equation (6) is satisfied.The convergence condition of the observer (11) can be formulated by the following Theorem.Theorem 2 [4]: The state error between the T-S descriptor model (3) and its observer (11) converges asymptotically towards zero, if there exist matrices 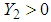 ,
, 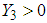 ,
, 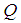 and
and 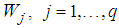 such that the following LMIs hold :
such that the following LMIs hold :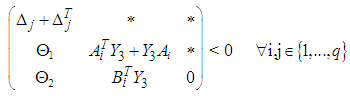 | (12) |
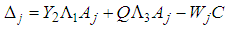 | (13) |
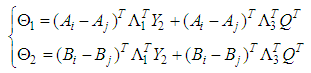 | (14) |
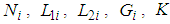 are given by:
are given by: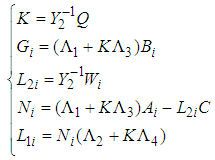 | (15) |
3. Main Result
- As mentioned above, based on the use of the state feedback given by (7) and the fuzzy observer (11), this section studies the problem of observer-based controller design for a class of TSDMs (3). Indeed, the following augmented system in closed-loop is considered:
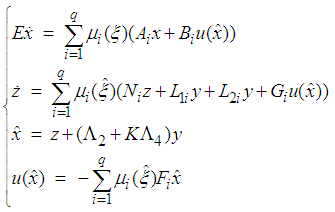 | (16) |
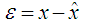 | (17) |
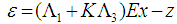 | (18) |
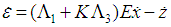 | (19) |
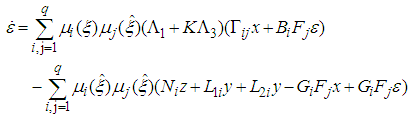 | (20) |
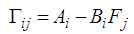 | (21) |
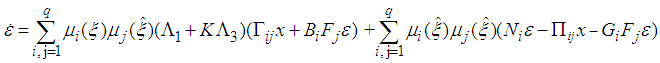 | (22) |
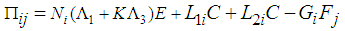 | (23) |
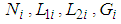 and
and 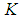 satisfy:
satisfy: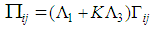 | (24) |
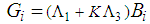 | (25) |
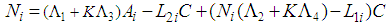 | (26) |
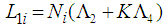 | (27) |
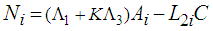 | (28) |
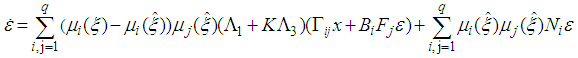 | (29) |
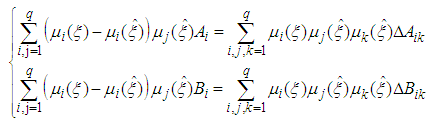 | (30) |
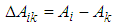 and
and 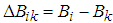 .Then, from (21), the equation (29) becomes:
.Then, from (21), the equation (29) becomes: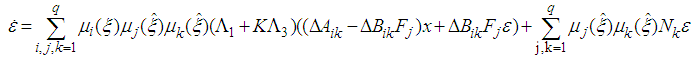 | (31) |
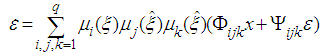 | (32) |
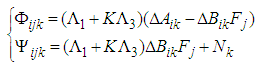 | (33) |
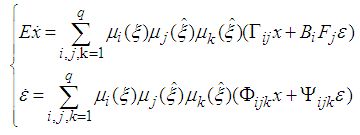 | (34) |
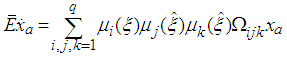 | (35) |
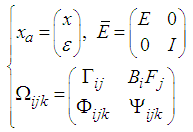 | (36) |
 ; there exist matrices
; there exist matrices 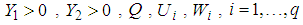 , verifying the following LMIs:
, verifying the following LMIs: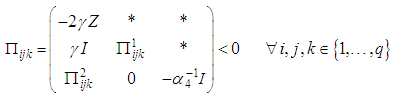 | (37) |
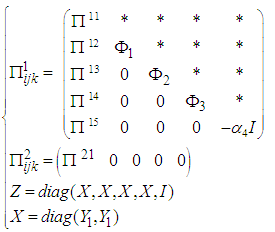 | (38) |
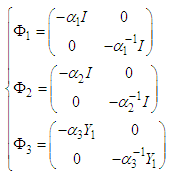 | (39) |
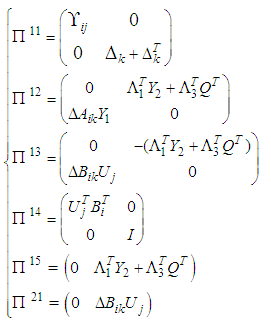 | (40) |
 and
and 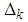 are defined in (9) and (13) respectively.The dynamic controller gains
are defined in (9) and (13) respectively.The dynamic controller gains 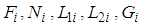 and
and 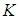 are given by:
are given by: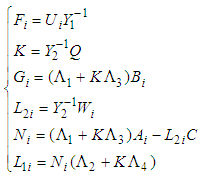 | (41) |
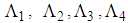 are such that (6) is satisfied.Proof of Theorem 3: To prove the convergence to zero of the state variable system (35), let us consider the candidate Lyapunov function as follows:
are such that (6) is satisfied.Proof of Theorem 3: To prove the convergence to zero of the state variable system (35), let us consider the candidate Lyapunov function as follows: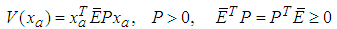 | (42) |
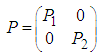 | (43) |
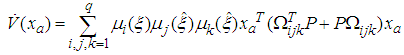 | (44) |
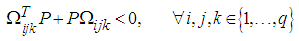 | (45) |
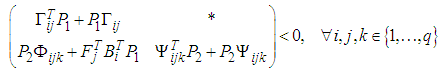 | (46) |
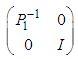 to both sides and defining new variables
to both sides and defining new variables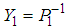 and
and 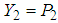 , thus we obtain:
, thus we obtain: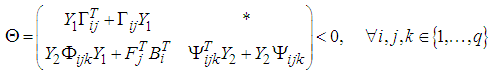 | (47) |
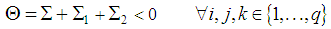 | (48) |
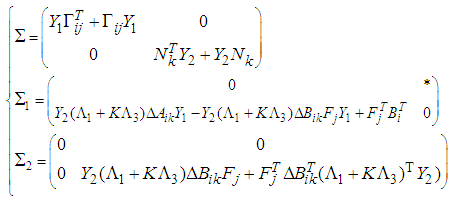 | (49) |
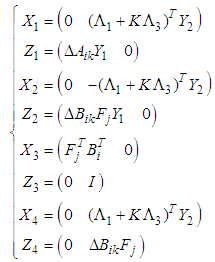 | (50) |
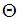 can be rewritten again as:
can be rewritten again as: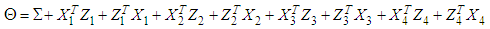 | (51) |
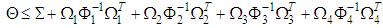 | (52) |
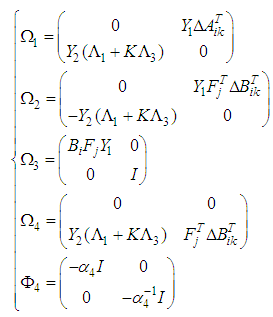 | (53) |
 are defined in (39).Hence, using the Schur complement [26], the inequality
are defined in (39).Hence, using the Schur complement [26], the inequality  hold if the following matrix inequality is satisfied:
hold if the following matrix inequality is satisfied: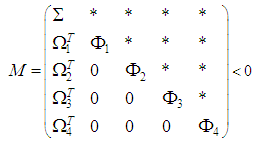 | (54) |
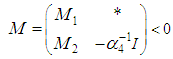 | (55) |
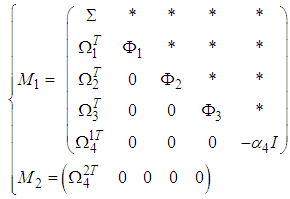 | (56) |
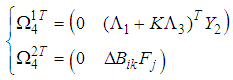 | (57) |
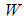 defined by:
defined by: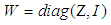 | (58) |
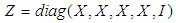 | (59) |
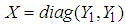 | (60) |
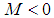 is equivalent to:
is equivalent to: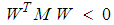 | (61) |
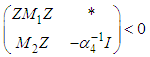 | (62) |
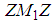 leads to:
leads to: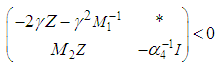 | (63) |
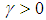 .Using the Schur complement, we obtain:
.Using the Schur complement, we obtain: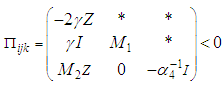 | (64) |
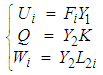 | (65) |
4. Illustrative Example
- To illustrate the efficiency of the proposed dynamic controller, we consider a rolling disc process described by the following TSDM with unmeasurable premise variable given in [25] such that the hypothesis H4) is satisfied:
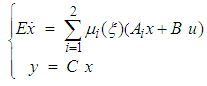 | (66) |
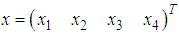 is the state vector with
is the state vector with 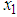 is the position of the center of the disc,
is the position of the center of the disc, 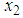 is the translational velocity of the same point,
is the translational velocity of the same point, 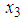 is the angular velocity of the disc,
is the angular velocity of the disc, 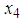 is the contact force between the disc and the surface.
is the contact force between the disc and the surface. 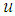 is the applied input force to the disc and
is the applied input force to the disc and 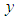 is the vector of output measurement.
is the vector of output measurement.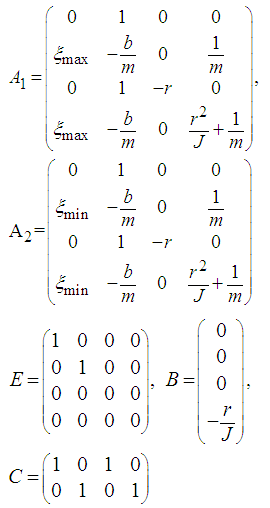 The weighting functions are defined by:
The weighting functions are defined by: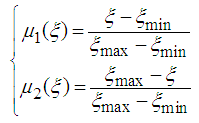 | (67) |
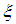 is the premise variable having for expression:
is the premise variable having for expression: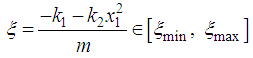 | (68) |
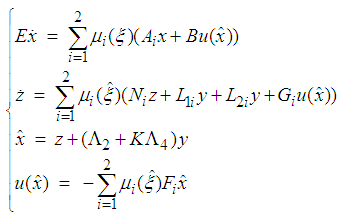 | (69) |
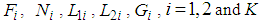 are the gains of the proposed dynamic controller. Notice that to apply the theorem 3 in order to calculate such dynamic controller gains; it suffices to rewritten system (69) into its equivalent representation (35) as mentioned in Section 3.Thus, in a first time, we calculate the matrices
are the gains of the proposed dynamic controller. Notice that to apply the theorem 3 in order to calculate such dynamic controller gains; it suffices to rewritten system (69) into its equivalent representation (35) as mentioned in Section 3.Thus, in a first time, we calculate the matrices 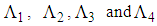 satisfying (6) from singular value decomposition of
satisfying (6) from singular value decomposition of 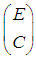 . Indeed, under hypothesis H4), the following numerical expressions of
. Indeed, under hypothesis H4), the following numerical expressions of 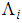 were obtained:
were obtained: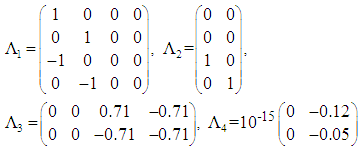 In a second time, we resolve the LMIs (37) in
In a second time, we resolve the LMIs (37) in 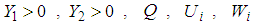 . Indeed, with
. Indeed, with 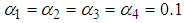 and
and 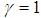 , we obtain the following dynamic controller gains calculated by (41):
, we obtain the following dynamic controller gains calculated by (41):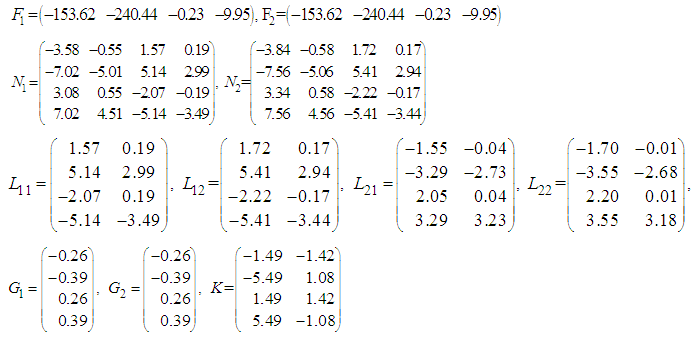 In order to illustrate the performances of the proposed observer-based controller, numerical simulations of system (69) were performed using a Runge-Kutta method combined with the Newton-Raphson algorithm. The following initial conditions of system (69) were used:
In order to illustrate the performances of the proposed observer-based controller, numerical simulations of system (69) were performed using a Runge-Kutta method combined with the Newton-Raphson algorithm. The following initial conditions of system (69) were used: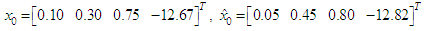 The simulation results of the system (69) with the dynamic controller gains
The simulation results of the system (69) with the dynamic controller gains 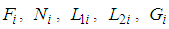 and
and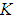 are given in Figures 1, 2, 3 and 4 where the dashed lines denote the state variables estimated by the fuzzy observer.These simulation results show the good performance of the proposed observer-based controller designed. Indeed, the global asymptotic stability of the augmented system (69) in closed-loop with the proposed observer-based controller is satisfied.
are given in Figures 1, 2, 3 and 4 where the dashed lines denote the state variables estimated by the fuzzy observer.These simulation results show the good performance of the proposed observer-based controller designed. Indeed, the global asymptotic stability of the augmented system (69) in closed-loop with the proposed observer-based controller is satisfied. 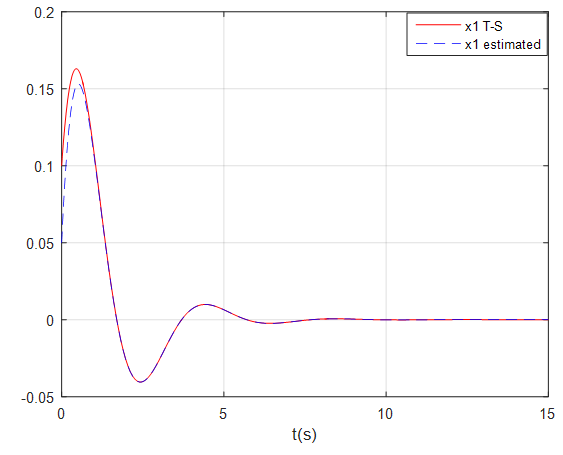 | Figure 1. 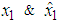 with fuzzy observer-based controller with fuzzy observer-based controller |
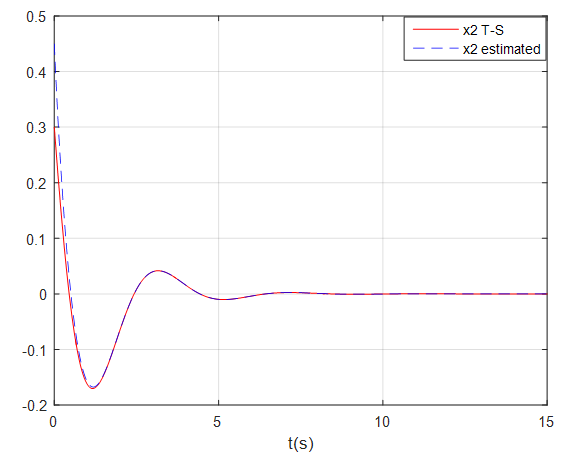 | Figure 2. 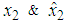 with fuzzy observer-based controller with fuzzy observer-based controller |
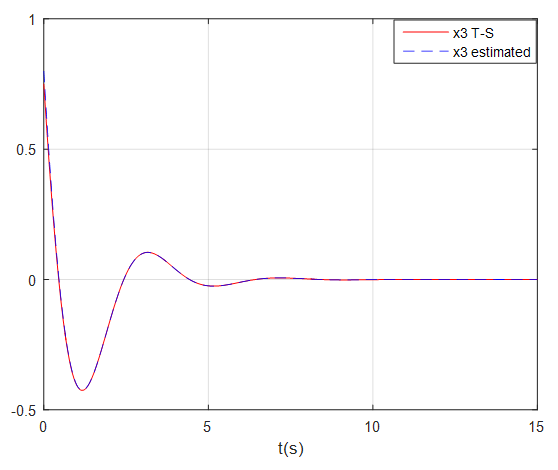 | Figure 3. 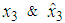 with fuzzy observer-based controller with fuzzy observer-based controller |
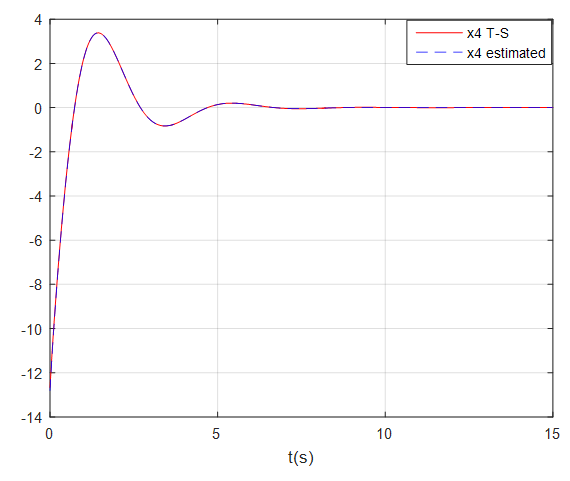 | Figure 4. 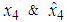 with fuzzy observer-based controller with fuzzy observer-based controller |
5. Conclusions
- In this paper, a new result of separation principle for a class of TSDMs with unmeasurable premise variables is suggested. More precisely, the proposed result concerns the real-time implementation without the use of an optimization algorithm of the static state feedback given in [3] by using the fuzzy observer proposed in [4]. The global asymptotic stability of the augmented system in closed-loop is studied by using the Lyapunov method and the stability conditions are given in terms of LMIs. The good performance of the proposed observer-based controller design is illustrated in simulation through a rolling disc process as an illustrative example.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML