Abolfazl Karimi, Mohammad Alikarami
School of Chemical Engineering, University of Tehran, Tehran, Iran
Correspondence to: Abolfazl Karimi, School of Chemical Engineering, University of Tehran, Tehran, Iran.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this research, simultaneous control of the level and the temperature in a tank has been studied. Firstly calibration of level and temperature sensors, control valve characterization, the relationship between outlet flow and level performed. Experimental characterization of the valve shows quick opening behavior for the valve, and linear relationship between level and outlet flow. Using mass and energy balances, linear system model proposed, and as a result, transfer functions determined. Experimental Ziegler Nichols tuning method with the unit step response have been utilized to derive first order, and first order with time delay transfer functions for level and temperature, respectively. P and PI controller parameters for level and temperature loops have been presented. All of the open loop transfer function derived experimentally and modified in Simulink environment for the design of dynamic decoupler. Computing relay has adjustable gain for the decoupling of control loops. Finally, the best model and decoupler obtained to compare with experimental results.
Keywords:
Level, Temperature, Interactive, Simulink, Modeling
Cite this paper: Abolfazl Karimi, Mohammad Alikarami, Experimental and Theoretical Investigation of Temperature and Level Interactive Control in a Tank, International Journal of Control Science and Engineering, Vol. 6 No. 2, 2016, pp. 38-48. doi: 10.5923/j.control.20160602.02.
1. Introduction
Sometimes in a chemical process it is obligatory to control several interactive variables simultaneously, these interactions should be removed with the control system. Distillation towers; reactors and mixing vessel and so on are common examples [12]. Two interacting control loops can be omitted, only if the process is defined completely and all transfer functions are precisely obtained. So determination of transfer function matrix enables design of decoupler [14].In this research, interactive temperature and level control loops have been operated in a tank. Corneili et al have used similar scheme, but in their study, hot water has been used for level and cold water for temperature control. Using different regulate PID controller setting theories and labview software they have demonstrated that ITAE and dual loop setting are the most accurate results [1]. Yamamoto has used adaptive controller for simultaneous temperature and level control in a condition that disturbance has a great effect on the process. Also, they have studied in a discrete domain and have designed static decoupler for removing or compensating the interaction. With minimization of variance control (GMVC1); parameters for PID controllers have attained automatically (Auto tuning). For this purpose, two online pre estimator for changing the pre compensators and as a result controller parameters has been used [3, 11]. Using the concept of relative gain Jiang calculated non diagonal elements with disturbance analysis and diagonal with main transfer functions and then equivalent closed loop transfer function derived for controller design [4]. Garcia has used (IMC2) for setting the PID control parameters in multivariable processes [10]. Kiong has used MPC method to multivariable ratio control homogeneous wafer temperature in microlithography [6]. Tan has performed integration in unit step response of level control in two series interactive tank model and has determined PID feedback controller and feed forward parameters with Root locus method [7]. Luan simplified the effective open loop transfer function for design multivariable control system with reduced order technique [5]. In this research all transfer functions have been obtained experimentally, mathematical modeling, interactive process and simulation in Simulink environment have been performed and modified comparing the results with experiment. Experiments have been done several times to examine repeatability and present best result.
2. Experiment
2.1. Process Description
Schematic of the process has been shown in fig 1. It consists of a tank with a diameter of 0.21 meters and two hot and cold inputs that are used to control temperature and level respectively. To investigate the interaction more precisely, the flow of hot and cold streams have been set the same amount. Outlet valve can be set manually. To set outlet valve, level and temperature loops were switched to manual with output of 100% then the valve was set, so that the level become steady in the level of 100. In this condition control loops are controllable in the range of 0-100. Industrial Electrical instruments in the process are used as shown in table 1.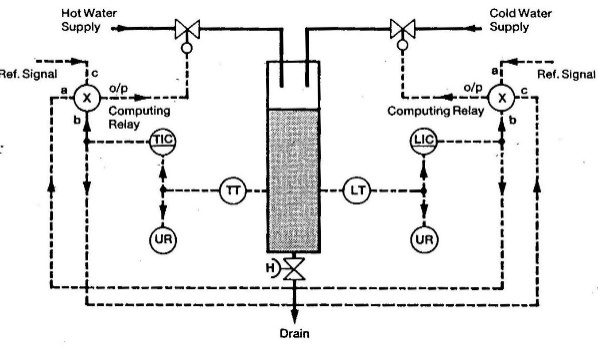 | Figure 1. System flow diagram |
Table 1. System components characterization
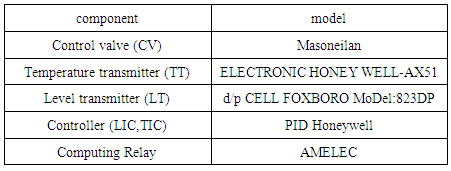 |
| |
|
2.2. Calibration
Comparing the actual level of the tank with PV of the controller gives the calibration curve of the level that is shown in fig 2. To calibrate the temperature sensor, temperature of the outlet flow when inlet flow is cold, hot and mixture of them has been measured with thermometer and compared with PV of the controller that is shown in fig 2.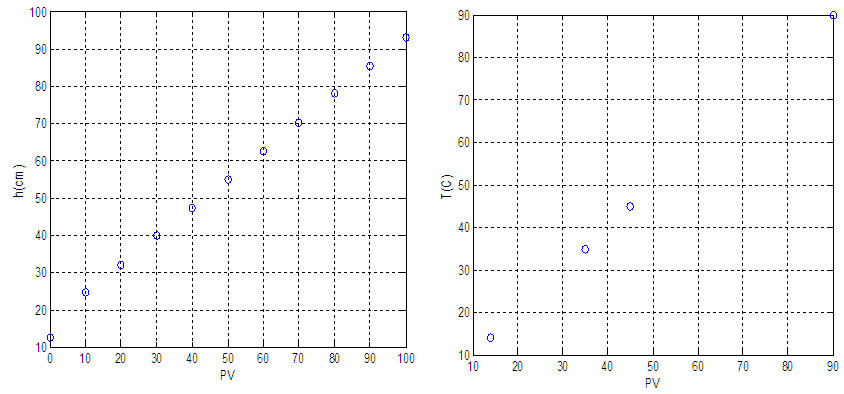 | Figure 2. Level and temperature calibration |
2.2.1. Control Valve Characterization
Industrial Control valves have been used. While the level controller is in manual mode, outlet of the controller changed from 0 to 100 and the corresponding flow for each output was measured that shown in fig 3. it demonstrates that the valve has a quick opening behavior3 [13].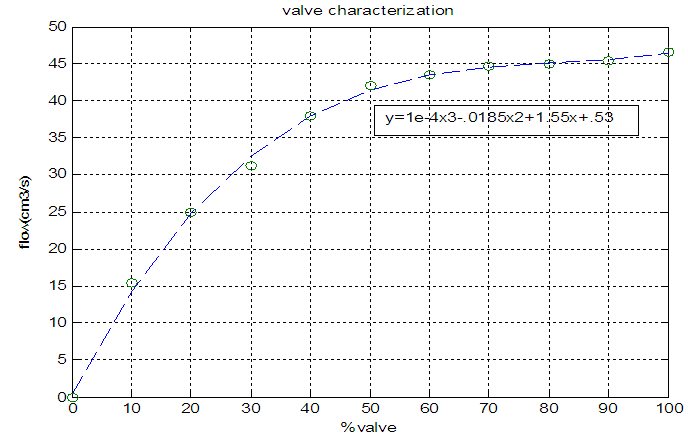 | Figure 3. Control valve characterization |
2.2.2. Outlet Flow and Level Relationship
To determine the exact relationship between outlet flow and tank level, level should be kept constant and flow be measured, so in a close loop state, by changing the level set point between 0 to 100 and measuring the steady state outlet flow in each level; characterization curve can be attained. Fig 4 shows the results. Linear relationship has been obtained by the least square method: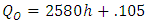 | (1) |
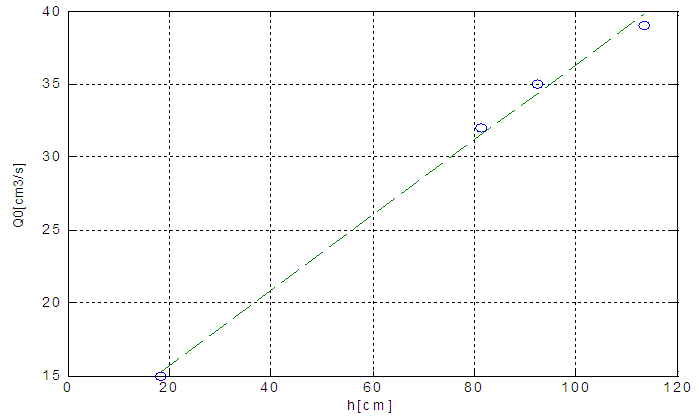 | Figure 4. Outlet flow as a function of level |
2.3. Controller Tuning
Level: the unit step response by changing the output of controller from 10 to 20% has been shown in fig 8. This response clearly demonstrates that the system has a first order dynamic with time constant of 1036 second and gain of 3.5.Proportional controller is suitable for this first order without time delay system. kc with Ziegler Nichols tuning method has been calculated to be 98.6.Temperature: while the level loop is closed; step change in output of temperature controller from 8 to 15 was imposed and resulting reaction curve is shown in fig 6. first order with transport delay model transfer function have been derived. controller parameter from Ziegler Nichols tuning method are 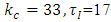 .
.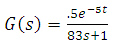 | (2) |
2.4. Closed Loop Control
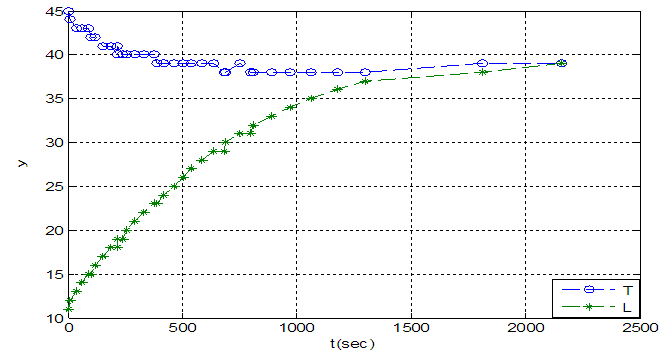
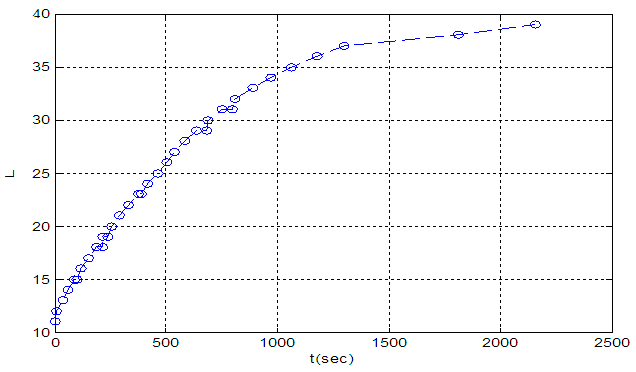
Simultaneous control of temperature and level loops is shown in fig 7. this figure shows that two control loops have interaction.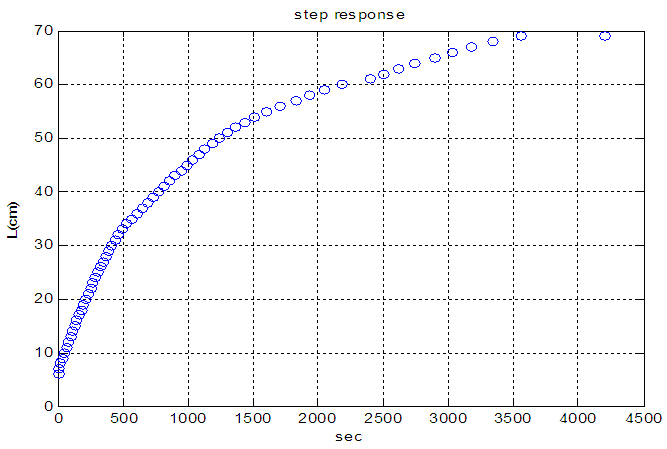 | Figure 5. System open loop response |
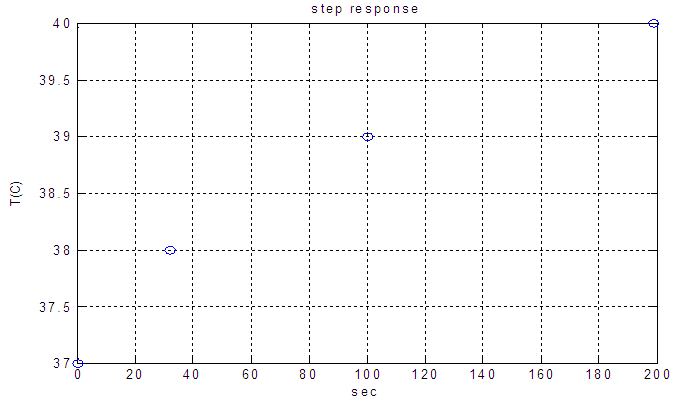 | Figure 6. Temperature response to unit step input |
 | Figure 7. Simultaneous temperature and level control |
2.5. Interactive Transfer Functions
Material and Energy balances: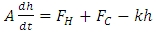 | (3) |
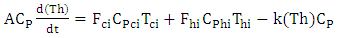 | (4) |
Deviation variables: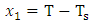 | (5) |
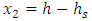 | (6) |
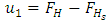 | (7) |
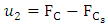 | (8) |
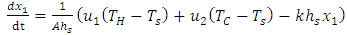 | (9) |
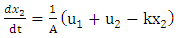 | (10) |
Matrix equations in state environment. 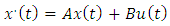 | (11) |
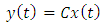 | (12) |
A, B and C are: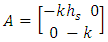 | (13) |
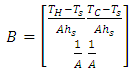 | (14) |
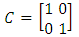 | (15) |
To calculate transfer functions from state environment, the equation 16 have been used [12].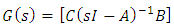 | (16) |
The transfer function is as follows: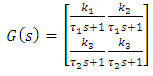 | (17) |
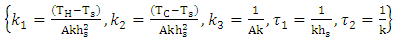 | (18) |
While two loops are open and output of level has become steady at 20%, temperature controller output changed from 12 to 22%, the results have been shown in fig 8.Calculated  , is shown in fig 9.First order model with
, is shown in fig 9.First order model with 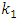 and
and 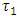 from (18) for
from (18) for 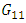 is proposed.
is proposed.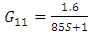 | (19) |
To determine 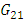 level change versus time has shown in fig 10.First order model with
level change versus time has shown in fig 10.First order model with 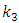 and
and 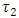 from eq (18) for
from eq (18) for 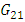 is proposed.
is proposed.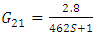 | (20) |
While both loops are open and temperature with (output= 12%) is in steady state. step change from 10 to 20% in level controller output resulted the following outputs that are shown in fig 11.In order to 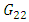 from these data, level and time function has been shown in fig 12.First order model with
from these data, level and time function has been shown in fig 12.First order model with 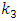 and
and 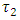 from (18) for
from (18) for 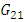 is proposed.
is proposed.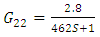 | (21) |
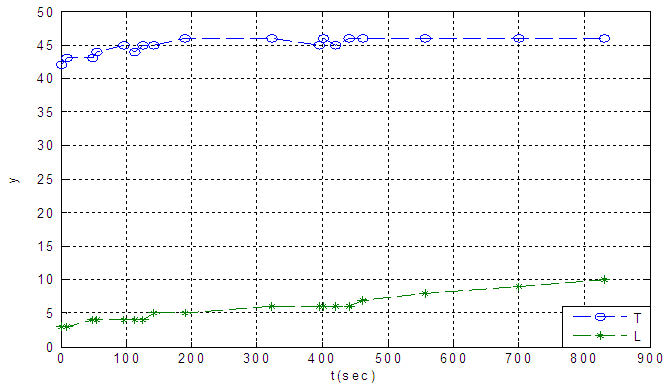
To determine 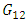 temperature change with time has depicted in fig 13.First order model with
temperature change with time has depicted in fig 13.First order model with 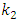 and
and 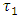 from (18) for
from (18) for 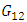 is proposed.
is proposed.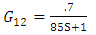 | (22) |
 | Figure 8. System open loop response to unit step change in hot flow |
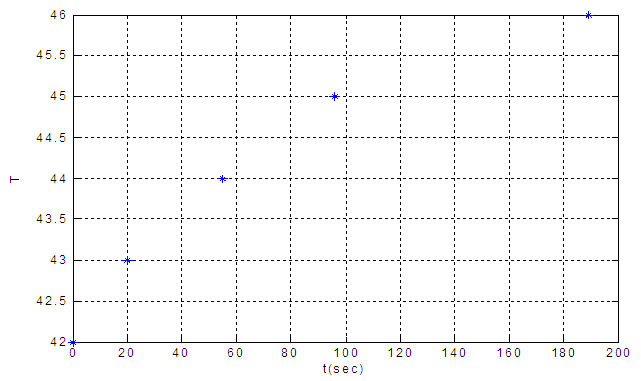 | Figure 9. Temperature variance versus time for determine G11 |
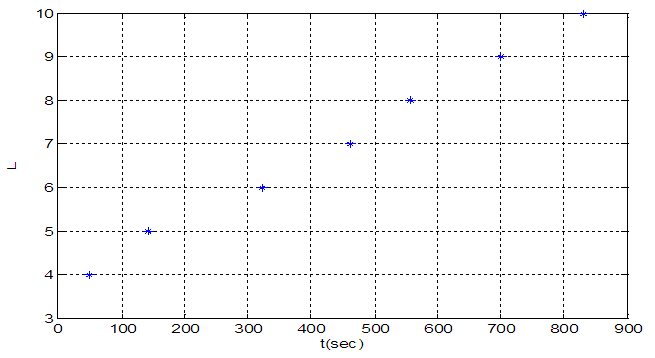 | Figure 10. Level change versus time for G21 |
 | Figure 11. Open loop response to step change in cold flow |
 | Figure 12. Level vs time for determination of G22 |
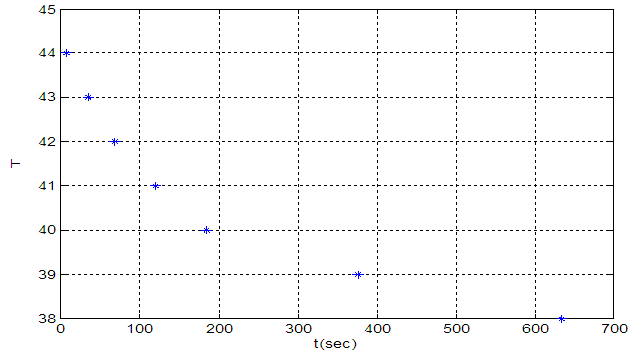 | Figure 13. Temperature change as a function of time for G12 calculation |
3. Results and Discussion
All of the experiments that were done with apparatuse simulated in Matlab (Simulink environment) and the results have been compared with experimental data and, to modify the model.
3.1. Simulation of Level Control in the Tank
Performance of the control system have been simulated according to the following block diagram.The experimental transfer function has been used in this block diagram. Experimental data and model closed loop with kc=100 compared in fig 15.While only level controller is closed there is a good agreement between experimental data and model.
3.2. Simulation of Simultaneous Temperature and Level Control in a Tank with Interaction
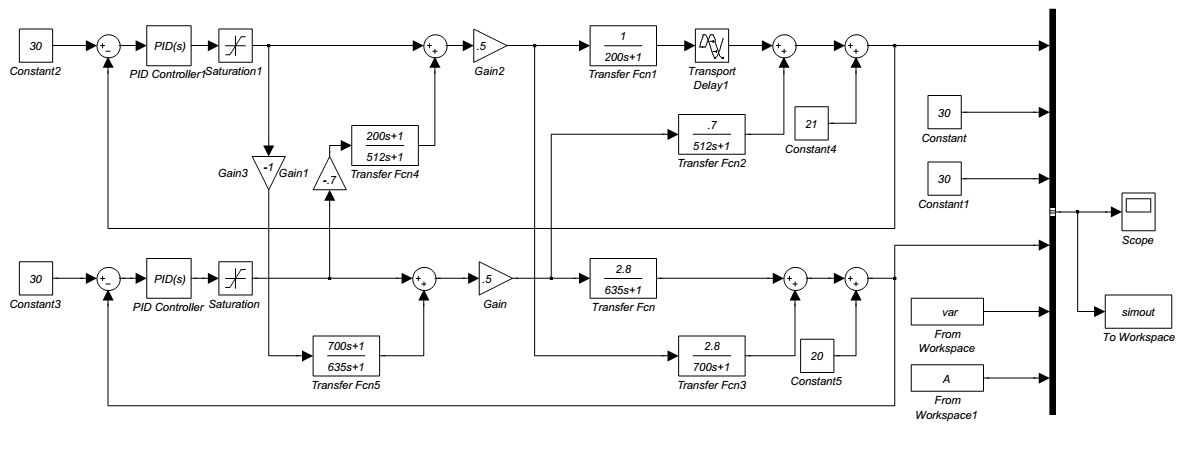
Using transfer functions calculated in 2-5 closed loop model has been designed in Simulink as shown in fig 16.The system response is different from experimental results. In this configuration G11 and G22 role as feedback; and G12 and G21 as feed forward controllers. In other words feedback loops reduce the feed forward uncertainties. G11 and G12 as well as G22 and G21 have similar time constants [8]. For modification of the model due to the fact that G11 and G22 are in feedback route and G12 and G21 are in feed forward routes; first level control alone is compared with experimental data and changing the parameters ti=0.5 and transport delay of 3 seconds gives the best agreement between results. The same procedure has been used for temperature loop too and transport delay of 5 seconds and changing the time constant and gain of the process resulted the best agreement. The modified block diagram while interactive transfer functions have been closed, are shown in fig 17. The resulting curve has been obtained and demonstrates good agreement between experiment and model.
3.3. Decoupler Design
Gain of de coupler has been proposed in table 2:Table 2. Gain of interactive
 |
| |
|
Output signal of controllers when output of another controllers change have been calculated below: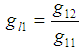 | (23) |
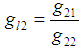 | (24) |
Every 3.5 part have been divided into 100 parts in de coupler system; so its gains are 71 and 18 respectively.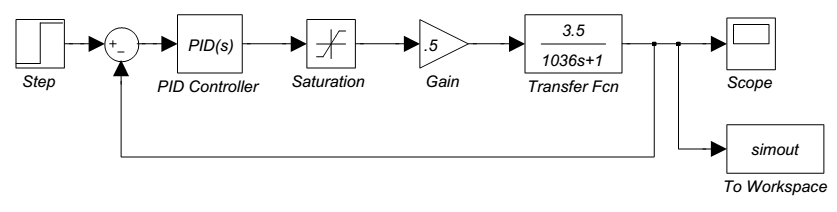 | Figure 14. Simulink block diagram of level control |
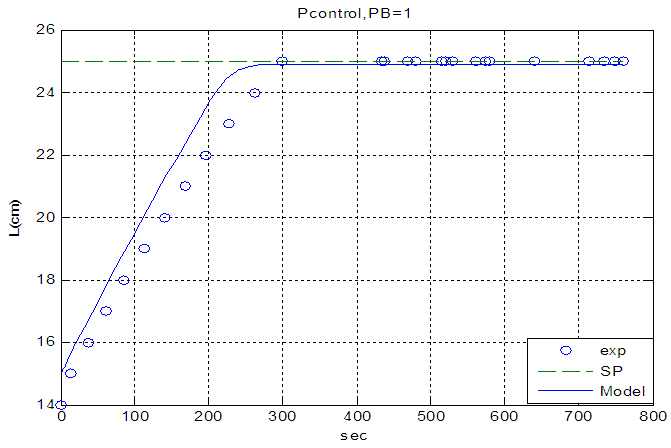 | Figure 15. Comparison of model and experimental result |
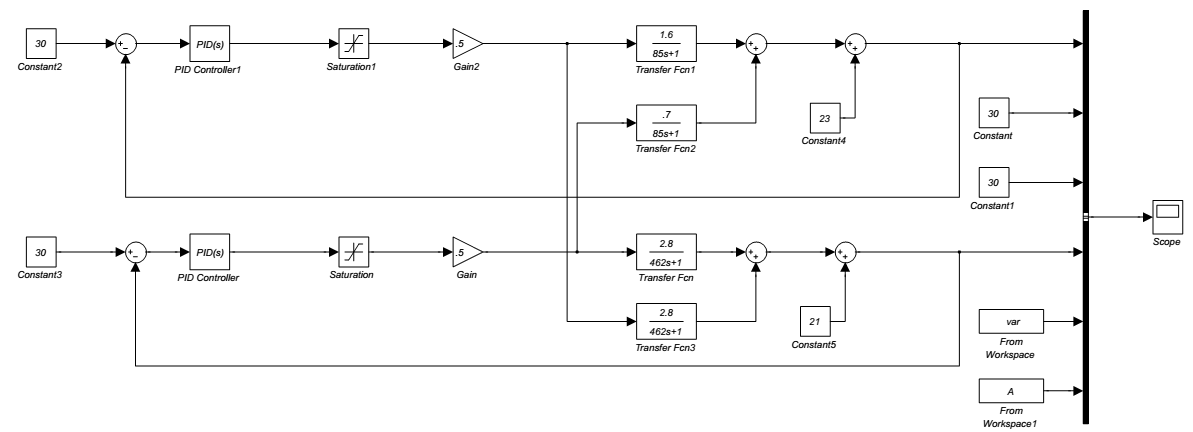 | Figure 16. Interactive level and temperature Simulink block diagram |
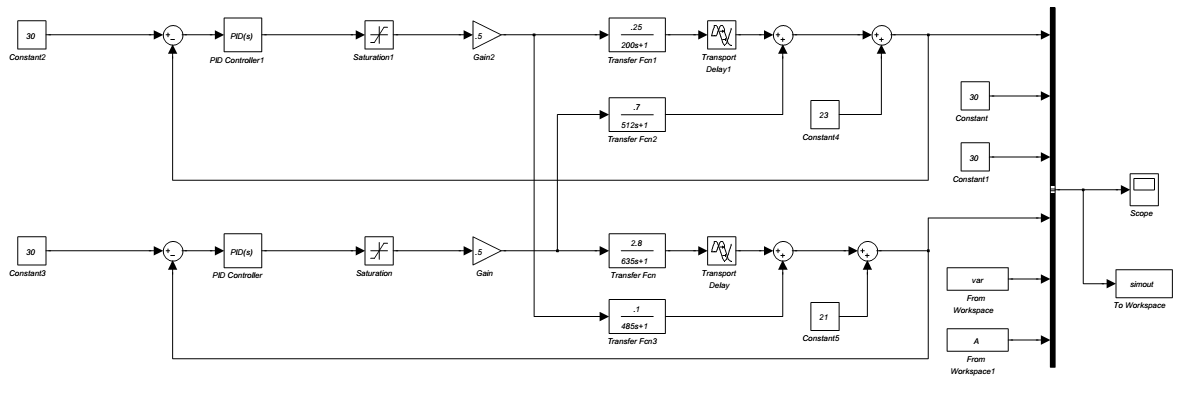 | Figure 17. Modified interactive level and temperature Simulink block diagram |
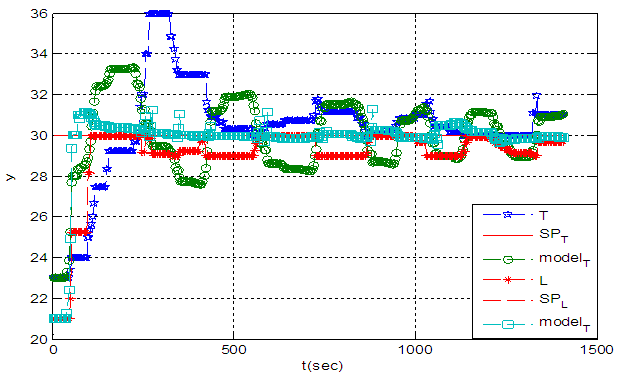 | Figure 18. Comparison of model and experimental result |
3.4. Experiments without Interaction
Using k1and k2 responses have been shown below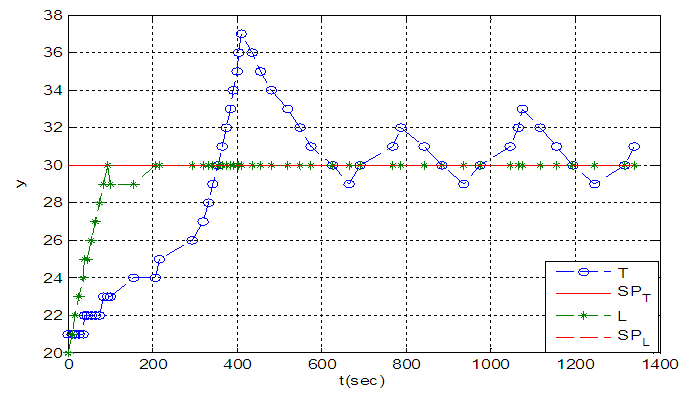 | Figure 19. Response of system without interaction |
 | Figure 20. Block diagram without interaction |
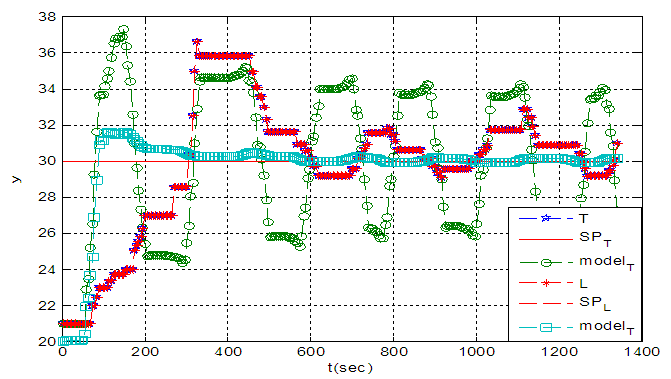 | Figure 21. Experimental and model response without interaction |
4. Conclusions
In this system, for level control solely there is no interaction so, according to obtained model and its first order characteristic, the level dynamic in the tank is integrator inherent so using a proportional controller in the closed loop response can omit the controller offset. For temperature loop PI controller have been designed. In this condition control loops have interactions. Feed forward and feedback transfer functions have calculated experimentally with open loop experiments. Static de couplers have been used to compensate the interactions in apparatus. De coupler gains have been calculated and the results show complete removal of interaction. In simulation environment using transfer functions the dynamic de couplers have been designed and simulation has been performed. Obtained models have been modified with experimental data.
Notes
1. General minimized variance control2. Internal Model Control3. Square root
References
| [1] | E. Cornieles, "Modeling and Simulation of a Multivariable Process Control, " IEEE ISIE 2006. |
| [2] | Nina F. Thornhill, "A continuous stirred tank heater simulation model with applications". Journal of Process Control, Volume 18, Issues 3–4, March 2008, Pages 347–360. |
| [3] | T. Yamamoto "Design and experimental evaluation of a multivariable self-tuning PID controller". IEE Proceedings - Control Theory and Applications (Volume: 151, Issue: 5). DOI: 10.1049/ip-cta:20040853. |
| [4] | Qiang Xiong, "Equivalent transfer function method for PI/PID controller design of MIMO processes" Journal of Process Control 17 (2007) 665–673. |
| [5] | Truong Nguyen Luan Vu, "Independent design of multi-loop PI/PID controllers for interacting multivariable processes". Journal of Process Control20 (2010) 922–933. |
| [6] | Kok Kiong Tan, "Predictive Ratio Control for Interacting Processes" Ind. Eng. Chem. Res. 2009, 48, 10515–10521. |
| [7] | Satean Tunyasrirut, "The Auto-Tuning PID Controller for Interacting Water Level Process" World Academy of Science, Engineering and Technology 12 2005. |
| [8] | Kurt. v. T. Waller. "Decoupling in Distillation", AIChE journal, Vol. 20, No.3, May 1974, page 592-594. |
| [9] | Qing-Guo Wang, “Decoupling internal model control for multivariable systems with multiple time delays "Chemical Engineering Science 57 (2002) 115 – 124. |
| [10] | C.E. Garcia, "Design Procedure for Multivariable Systems", American Chemical Society, 472-484, 1985. |
| [11] | K. B. Haggblom, "Experimental Comparison of Conventional and Nonlinear Model Based Control of a Mixing Tank "American Chemical Society, 1993. |
| [12] | BABATUNDE A. OGUNNAIKE,W. HARMON RAY "process dynamics, modeling, and control.", Oxford University Press. |
| [13] | Donald R Coughanowr, "Process Systems: Analysis and Control", McGraw-Hill Global Education Holdings, LLC. |
| [14] | Stephanopoulos, George "chemical process control: an introduction to the theory and practice" Prentice-Hall, 1984. |





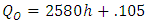

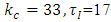 .
.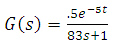



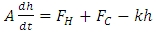
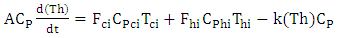
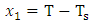
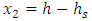
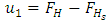
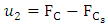
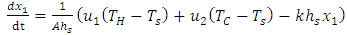
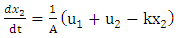
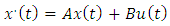
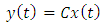
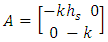
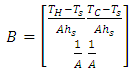
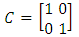
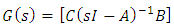
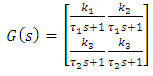
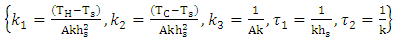
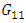 , is shown in fig 9.First order model with
, is shown in fig 9.First order model with 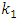 and
and 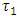 from (18) for
from (18) for 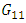 is proposed.
is proposed.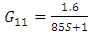
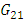 level change versus time has shown in fig 10.First order model with
level change versus time has shown in fig 10.First order model with 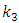 and
and 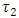 from eq (18) for
from eq (18) for 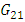 is proposed.
is proposed.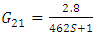
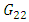 from these data, level and time function has been shown in fig 12.First order model with
from these data, level and time function has been shown in fig 12.First order model with 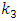 and
and 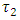 from (18) for
from (18) for 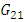 is proposed.
is proposed.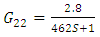
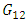 temperature change with time has depicted in fig 13.First order model with
temperature change with time has depicted in fig 13.First order model with 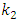 and
and 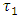 from (18) for
from (18) for 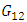 is proposed.
is proposed.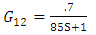






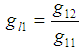
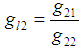








 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
