-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2016; 6(2): 23-37
doi:10.5923/j.control.20160602.01

Control of Periodic and Chaotic Motions in a Cantilever Beam with Varying Orientation under Principal Parametric Resonance
Usama H. Hegazy
Department of Mathematics, Faculty of Science, Al-Azhar University, Gaza, Palestine
Correspondence to: Usama H. Hegazy, Department of Mathematics, Faculty of Science, Al-Azhar University, Gaza, Palestine.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The principal parametric nonlinear response and control of a cantilever beam with varying orientation under direct and parametric excitations are analyzed and studied. The cantilever beam is modeled by a second order nonlinear ordinary differential equation. Various control techniques are proposed and numerical integration is performed to investigate the effectiveness of the applied controllers and time histories of the beam at the principal parametric resonance case. Approximate solution is sought applying the method of the multiple scales and the effect of the parameters on the stability of the nonlinear response is examined.
Keywords: Control, Periodic motion, Chaotic motion, Principal parametric resonance
Cite this paper: Usama H. Hegazy, Control of Periodic and Chaotic Motions in a Cantilever Beam with Varying Orientation under Principal Parametric Resonance, International Journal of Control Science and Engineering, Vol. 6 No. 2, 2016, pp. 23-37. doi: 10.5923/j.control.20160602.01.
Article Outline
1. Introduction
- The stability and bifurcation of subharmonic motions of a parametrically excited flexible rod are investigated using Melnikov asymptotic method [1]. The vibration control of one dimensional cantilever beam of varying orientation under external and parametric excitations is studied and analyzed. The cubic velocity feedback control is applied and the method of multiple scaled is utilized to construct the modulation equations of the amplitudes and phases. Numerical simulations are performed to investigate the effects of system parameters and the stability [2]. The nonlinear vibration and saturation phenomenon are analyzed in the controlled hinged-hinged flexible beam. The performance of different control techniques are studied and found that the oscillations of the system can be controlled actively via negative velocity feedback. Effects of system parameters are also investigated [3]. A control law based on quintic velocity feedback is proposed to reduce the vibrations of one dimensional cantilever beam under primary and parametric excitations. Numerical simulations are performed to verify analytical results obtained using the multiple scales method and to detect chaos and unbounded motions [4]. The chaotic motion of the nonlinear cantilever beam under harmonic axial excitation and transverse excitations at the free end is investigated. A new force control approach is proposed to control the chaotic response of the system considering the case of two-to-one internal resonance, principal parametric resonance-1/2 subharmonic resonance for the in-plane mode and fundamental parametric resonance-primary resonance for the out-of-plane mode [5, 6]. Subharmonic resonances of order one-half with fundamental parametric resonances are analyzed and studied in a single-degree-of-freedom system with quadratic and cubic nonlinearities. The steady-state solutions and their stability are determined applying the method of multiple scales [7]. The nonlinear response in the first vibration mode of a clamped-clamped beam subject to a subharmonic resonance of order one-half is investigated theoretically and experimentally. The multi-mode Galerkin method is used to discretize the governing partial differential equation into a set of coupled ordinary differential equations that are solved using the multiple scales method [8]. The nonlinear response of a post-buckled beam under harmonic axial load is analytically studied with five subharmonic resonances utilizing the multiple scales method. The steady-state solutions are obtained and their stability are investigated [9]. The method of multiple scales is used to obtain analytical solution for the nonlinear differential equations describing the motion of the controlled electromechanical system with time-varying stiffness. Negative linear, quadratic, and cubic velocity feedback controllers are applied to the system and investigated. It is found that the vibration of the seismograph model is best controlled via the negative velocity feedback [10]. A nonlinear cantilever beam of varying orientation with time-delay subject to direct and parametric excitations is studied at the primary and parametric resonances. The first order approximation of the response is obtained using the multiple scales method, where the time delay is presented in the proportional feedback and the derivative feedback [11]. The Melnikov method is used to determine the homoclinic and heteroclinic chaos in the micromechanical resonators. Numerical simulations including basin of attraction and bifurcation diagrams reveal the effect of parametric excitation on the system transition to chaos and confirm analytical predictions. Moreover, the time-varying stiffness is introduced to control the chaotic motion of the system [12]. The nonlinear response of a Timoshenko beam having a randomly varying stiffness and loss factor at its support is studied under harmonic moving load. The mean value and standard deviation of the beam responses are calculated using the first-order two dimensions perturbation method [13]. The numerical Runge-Kutta method with variable step-size is applied to explore the subharmonic dynamics of an axially accelerating beam. It is found that the variation of the mean value of the speed and the amplitude of the speed affect the periodic, quasiperiodic, and chaotic responses of the system [14]. The method of multiple scales is used to analyze the nonlinear flexural vibrations of a microcantilever beam with a piezoelectric actuator layer on the top side of the beam. The obtained analytical and numerical results are verified experimentally [15]. An acceleration feedback controller technique is proposed to reduce the oscillations in a class of multi degrees-of-freedom mechanical systems. The control cost and robustness of the controller are taken into account when choosing the control parameters. Numerical simulations are carried out to verify analytical predictions. A nonlinear velocity feedback control method for inducing natural oscillations in a class of two degrees-of-freedom mechanical systems is proposed and investigated [16, 17]. A new control method that combines sliding mode control (SMC) and positive position feedback control (PPF) is proposed to suppress the vibration of a beam subjected to a moving mass. Combining both control methods is found to overcome problems arise when applying each method separately. Numerical examples are given to demonstrate the effectiveness of the proposed method [18]. The positive position feedback (PPF) method, the integral resonant control (IRC) method and a new nonlinear integral positive position feedback (NIPPF) are considered and analyzed for vibration suppression of nonlinear systems. The method of multiple scales is utilized to solve the closed-loop system. It is found that the NIPPF controller has excellent results compared to the other two methods as it reduces the vibration at the exact resonant frequency. Also the subsequent peaks in the frequency domain are significantly suppressed [19]. The horizontal vibration of a magnetically levitated system with quadratic and cubic nonlinearities under primary and parametric excitations is investigated. A proportional- derivative controller is applied to suppress the oscillations of the resonant system. The method of multiple scales is used to obtain a second order approximate solution, which is compared numerically [20]. Displacement-velocity feedback and a linear classical control algorithm with a time varying gain matrix are proposed to reduce the vibration of a nanotube structure under a moving nanoscale particle. The performance of the applied control method with different numbers of the controlled modes and control forces along with the effects of the moving nanoparticle velocity and slenderness deflection are studied [21]. An electromechanical transducer, which consists of a mechanical oscillator linked to an electronic circuit is studied and two nonlinear control techniques are proposed to improve the transient response and to keep the system into the required periodic motion by avoiding both the chaotic and resonant behaviors. The control techniques are the optimal linear feedback and the state dependent Riccati equation. Numerical simulations are carried out to compare both methods and the energy transfer pumping between the electrical part and mechanical part is investigated [22].In this study, controlling the periodic and chaotic nonlinear responses of a nonlinear beam with varying orientation under principal parametric resonance case are studied numerically and analytically. The multiple scales analytical method and Rung-Kutta numerical method are applied and the stability of the beam model and effect of the system parameters are investigated using the time-histories, the phase portraits and the frequency response curves at the principal parametric resonance condition.
2. Mathematical Model
- The governing equation of motion to be studied and solved has the from
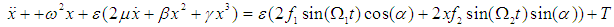 | (1) |
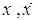 and
and 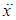 are the displacement, velocity and acceleration, ε is a small bookkeeping perturbation parameter, µ is the damping coefficient, ω is the natural frequency, β and γ are quadratic and cubic nonlinear terms, f1 and f2 are the external and parametric forcing amplitudes, Ω1,2 are the forcing frequencies, α is the orientation angle of the beam and T is a control input.
are the displacement, velocity and acceleration, ε is a small bookkeeping perturbation parameter, µ is the damping coefficient, ω is the natural frequency, β and γ are quadratic and cubic nonlinear terms, f1 and f2 are the external and parametric forcing amplitudes, Ω1,2 are the forcing frequencies, α is the orientation angle of the beam and T is a control input.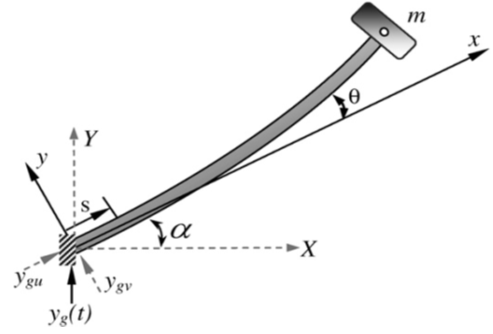 | Figure 1. The considered model of a cantilever beam |
3. Time-History and Phase-Portrait Solution
- Equation (1) is solved numerically using Runge-Kutta fourth order and the time histories and final phase portraits are plotted when the values for the system parameters are chosen as follows: µ=0 .02, ω = 10.9, f1 = 1.5, f2 = 1.2, Ω1 = 10.4, Ω2 = 9.9, β = 10.0, γ = 2.03, α = 10o with initial condition x(0)=0.1 and zero initial velocity, unless otherwise specified. Figure 2(a) shows a modulated vibration for the beam at nonresonance, while Fig. 2(b) shows the oscillations of the system at the principal parametric resonance case (Ω = 2ω) and the final phase-planes indicate fine limit cycles for both cases. Comparing the nonresonant and resonant solutions illustrates that the maximum steady-state amplitude at resonance has increased to about 115%. The principal parametric resonance solution will be considered as basic case in the following investigations. It can be seen from Figs. 2(c) (i - iv), that as the initial conditions are different, the steady-state solutions are different.
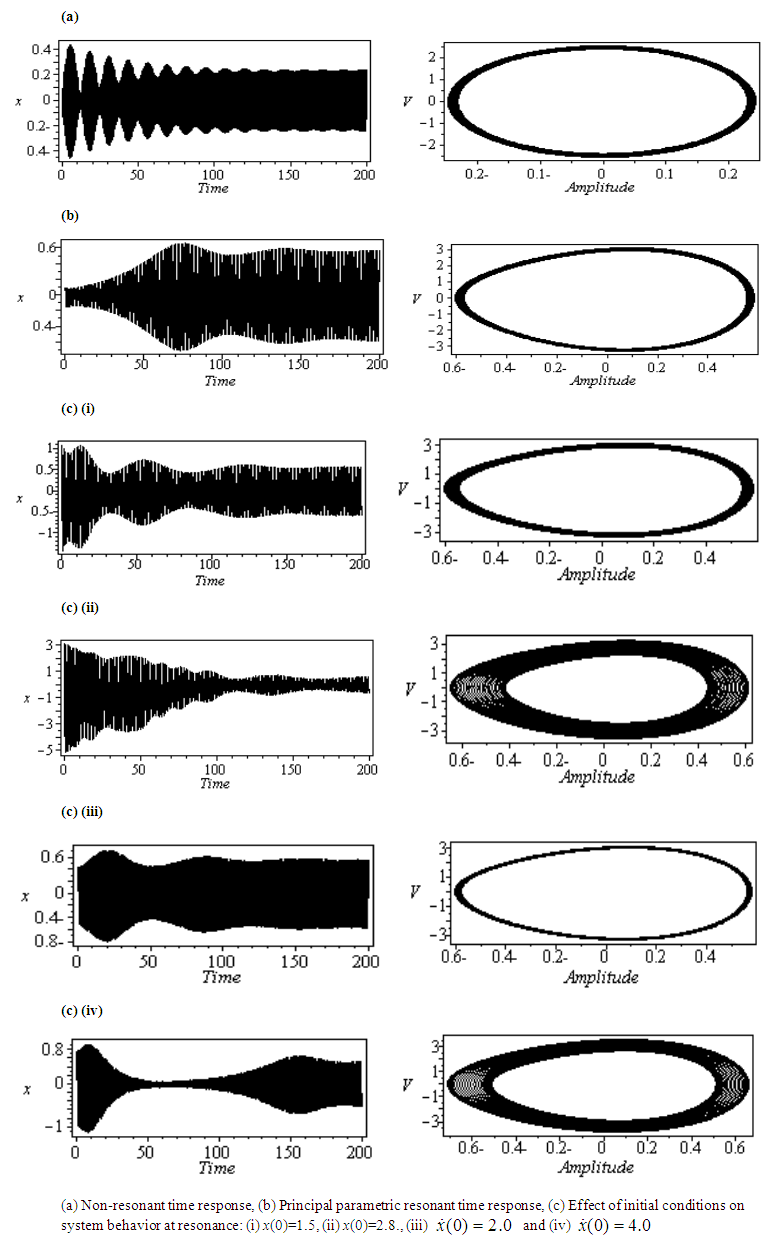 | Figure 2. Numerical solution of the cantilever beam |
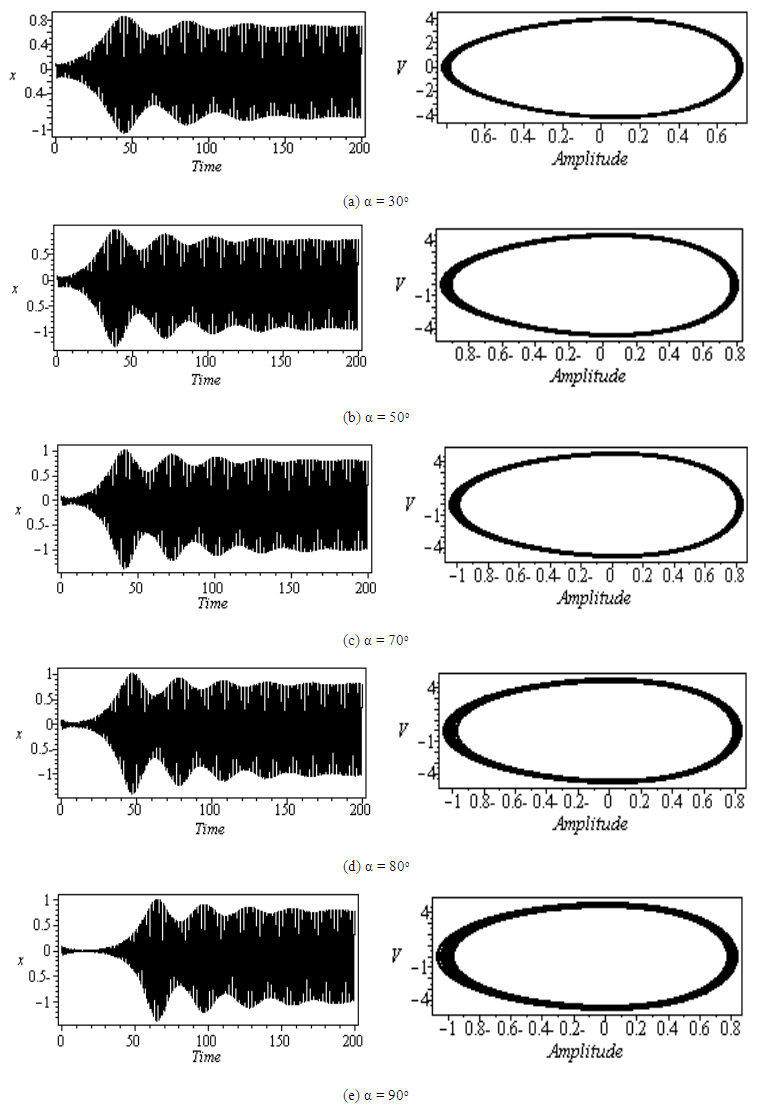 | Figure 3. Effect of the orientation angle at principal parametric resonance |
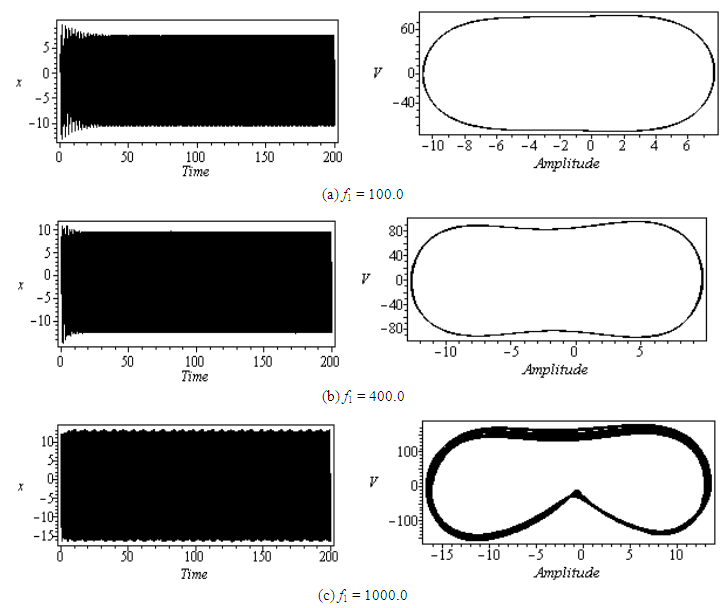 | Figure 4. Effect of the external excitation at principal parametric resonance |
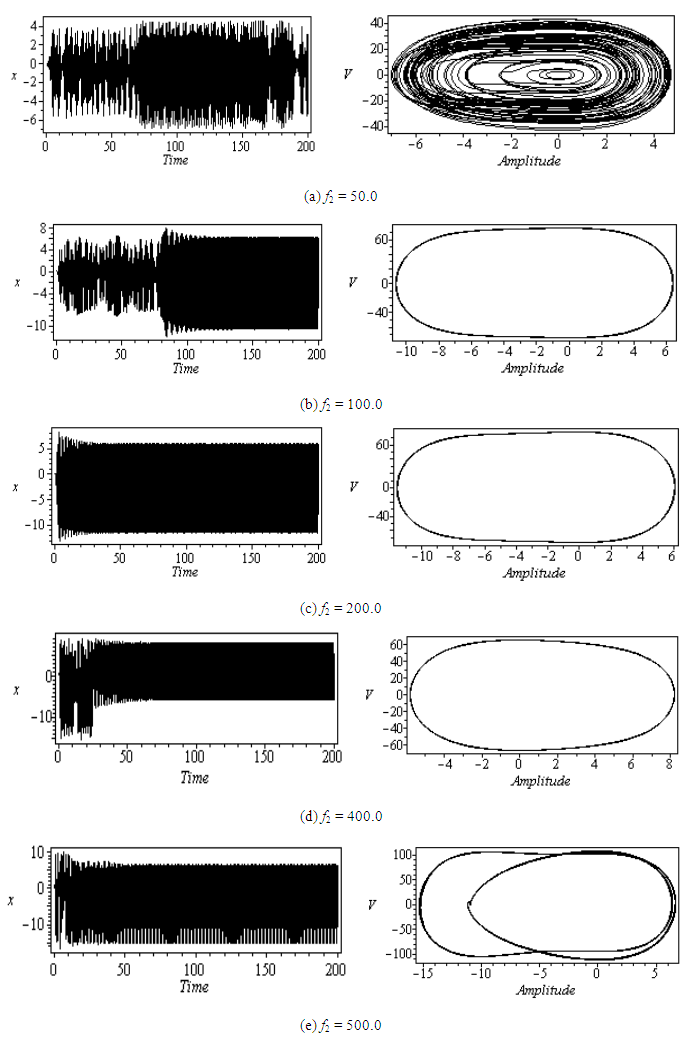 | Figure 5. Effect of the parametric excitation at principal parametric resonance |
3.1. Effects of Different Parameters
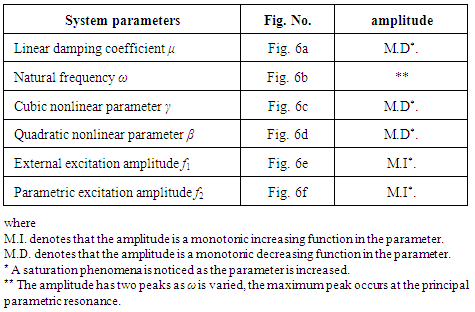
- Figure 6 shows the effect of different coefficients on the steady-state amplitude of the resonant beam, which is summarized in table 1.
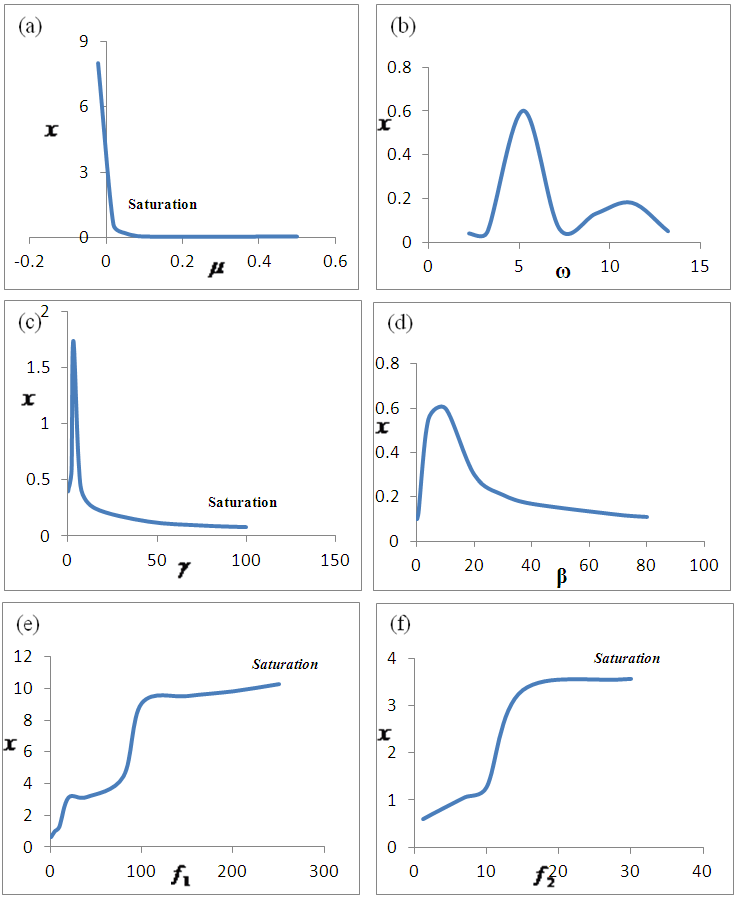 | Figure 6. Effect of the parameters at principal parametric resonance - numerical integration of the system: (x-axis: the parameter, y-axis: x-amplitude) |
|
3.2. Effect of the Gain Coefficient G
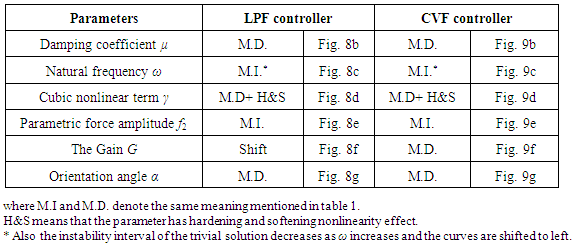
- Figure 7 shows the effect of suppressing the steady-state amplitude of the beam for various values of the gain when different controllers are applied. Three position feedback (PF) laws
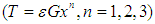 and three negative velocity feedback (VF) laws
and three negative velocity feedback (VF) laws 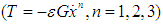 . The effectiveness of each control law is evaluated and represented by Ea = steady-state amplitude of the system before control / steady-state amplitude of the system after control, which is calculated at saturation beginning. Comparing the effectiveness of these controllers. It is noticed from Fig. 7(a) that: Ÿ Ea = 15.0, 15.0, and 6.0 and saturation begins at G greater than 5.0, 15.0, and 70.0 to control the system when applying linear (L), quadratic (Q), and cubic (C) PF controllers, respectively. This means that the LPF controller (T = εGx) is the best one among PF controllers.Whereas Fig. 7(b) indicates that:Ÿ Ea = 1.2, 1.2, and 1.2 and saturation begins at G greater than 0.5, 0.5, and 0.2 to control the system when applying linear (L), quadratic (Q), and cubic (C) VF controllers, respectively. This means that the CVF controller
. The effectiveness of each control law is evaluated and represented by Ea = steady-state amplitude of the system before control / steady-state amplitude of the system after control, which is calculated at saturation beginning. Comparing the effectiveness of these controllers. It is noticed from Fig. 7(a) that: Ÿ Ea = 15.0, 15.0, and 6.0 and saturation begins at G greater than 5.0, 15.0, and 70.0 to control the system when applying linear (L), quadratic (Q), and cubic (C) PF controllers, respectively. This means that the LPF controller (T = εGx) is the best one among PF controllers.Whereas Fig. 7(b) indicates that:Ÿ Ea = 1.2, 1.2, and 1.2 and saturation begins at G greater than 0.5, 0.5, and 0.2 to control the system when applying linear (L), quadratic (Q), and cubic (C) VF controllers, respectively. This means that the CVF controller 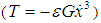 is the best one among VF controllers. In the next section we shall investigate the performance of the LPF and the negative CVF analytically using the method of multiple scales.
is the best one among VF controllers. In the next section we shall investigate the performance of the LPF and the negative CVF analytically using the method of multiple scales.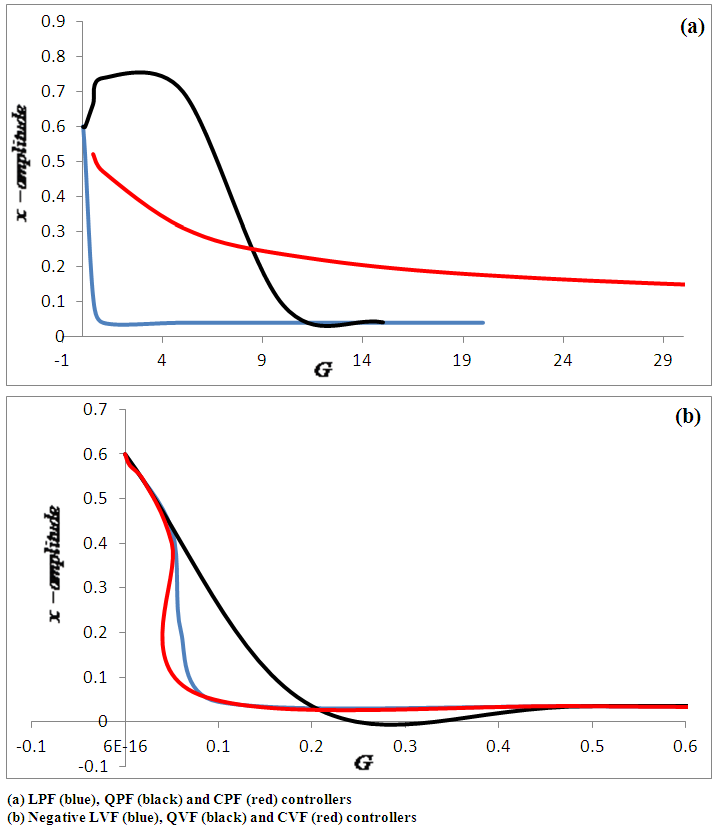 | Figure 7. Effect of the gain for various control laws at principal parametric resonance - numerical solution: (x-axis: the gain, y-axis: x-amplitude) |
4. Analytical Solution
- In this section the approximate solution of the nonlinear system, Eq. (1) with the two effective controllers is analyzed applying the method of multiple scales.
4.1. Linear Position Feedback Controller (LPF)
- Setting T = εGx in Eq. (1) and assuming
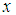 is in the form
is in the form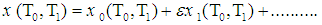 | (2) |
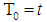 is the fast time scale and
is the fast time scale and 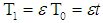 is the slow time scale. The time derivatives are expressed as
is the slow time scale. The time derivatives are expressed as 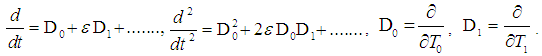 Equating the coefficient of same powers of ε yields:
Equating the coefficient of same powers of ε yields: 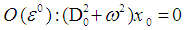 | (3) |
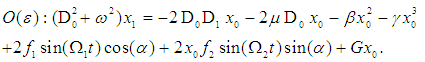 | (4) |
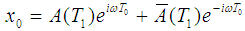 | (5) |
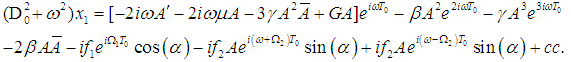 | (6) |
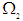 is very close to twice
is very close to twice 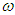 , which is expressed as
, which is expressed as 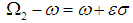 | (7) |
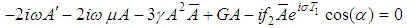 | (8) |
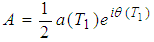 | (9) |
 are the steady-state amplitude and phase of the motion. Then Separating imaginary and real parts, and setting
are the steady-state amplitude and phase of the motion. Then Separating imaginary and real parts, and setting 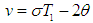 we obtain
we obtain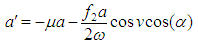 | (10) |
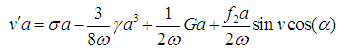 | (11) |
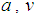 that is
that is 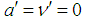 Thus Eqs. (11) and (12) can be reduced to the following nonlinear algebraic equations
Thus Eqs. (11) and (12) can be reduced to the following nonlinear algebraic equations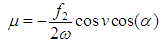 | (12) |
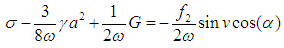 | (13) |
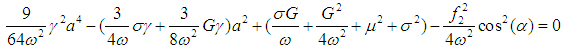 | (14) |
4.2. Negative Cubic Velocity Feedback Controller (CVF)
- Setting
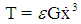 in Eq. (1) and following the same procedure as in LPF controller, considering the principal parametric resonance case, one obtains the solvability condition as
in Eq. (1) and following the same procedure as in LPF controller, considering the principal parametric resonance case, one obtains the solvability condition as 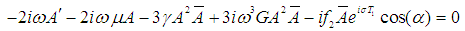 And the frequency response equation is given by
And the frequency response equation is given by 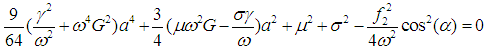 | (15) |
4.3. Trivial Solution
- To determine the stability of the trivial solutions, one investigates the principal parametric resonant solution with LPF control by introducing the following Cartesian form
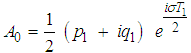 | (16) |
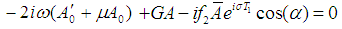 | (17) |
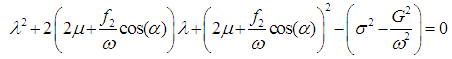 | (19) |
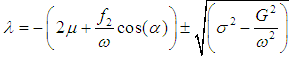 | (18) |
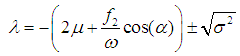 | (19) |
4.4. Analytical Results
- In this section, the fixed point response of the system is obtained by solving the frequency response equations (14) and (15) numerically. The representative solutions are illustrated by the amplitude-detuning parameter plots of Figs. (8), (9) and by the amplitude-force plots of Figs. (10), (11) with LPF and CVF controls for different values of other parameters.
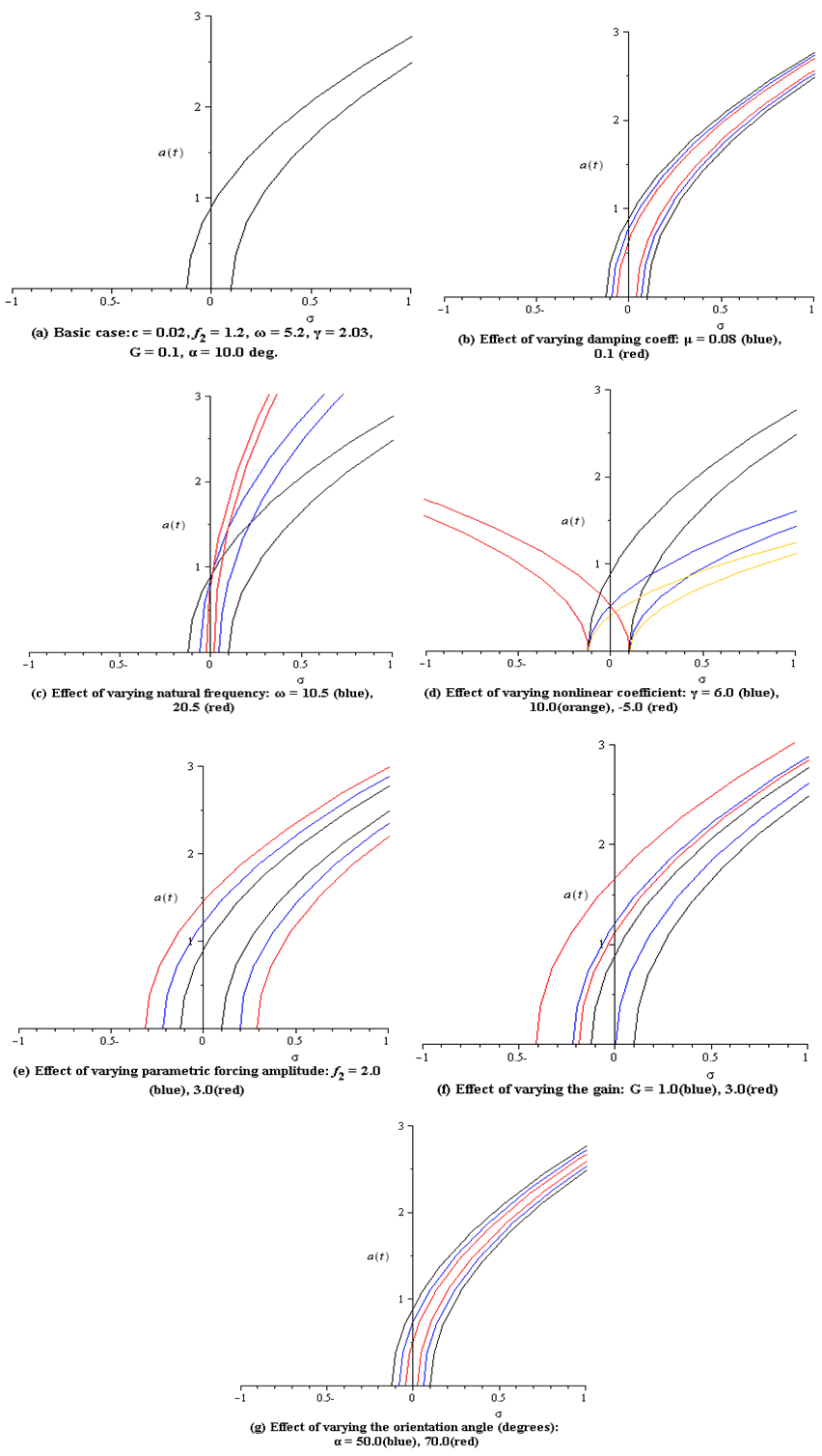 | Figure 8. Principal parametric frequency response curves with LPF controller |
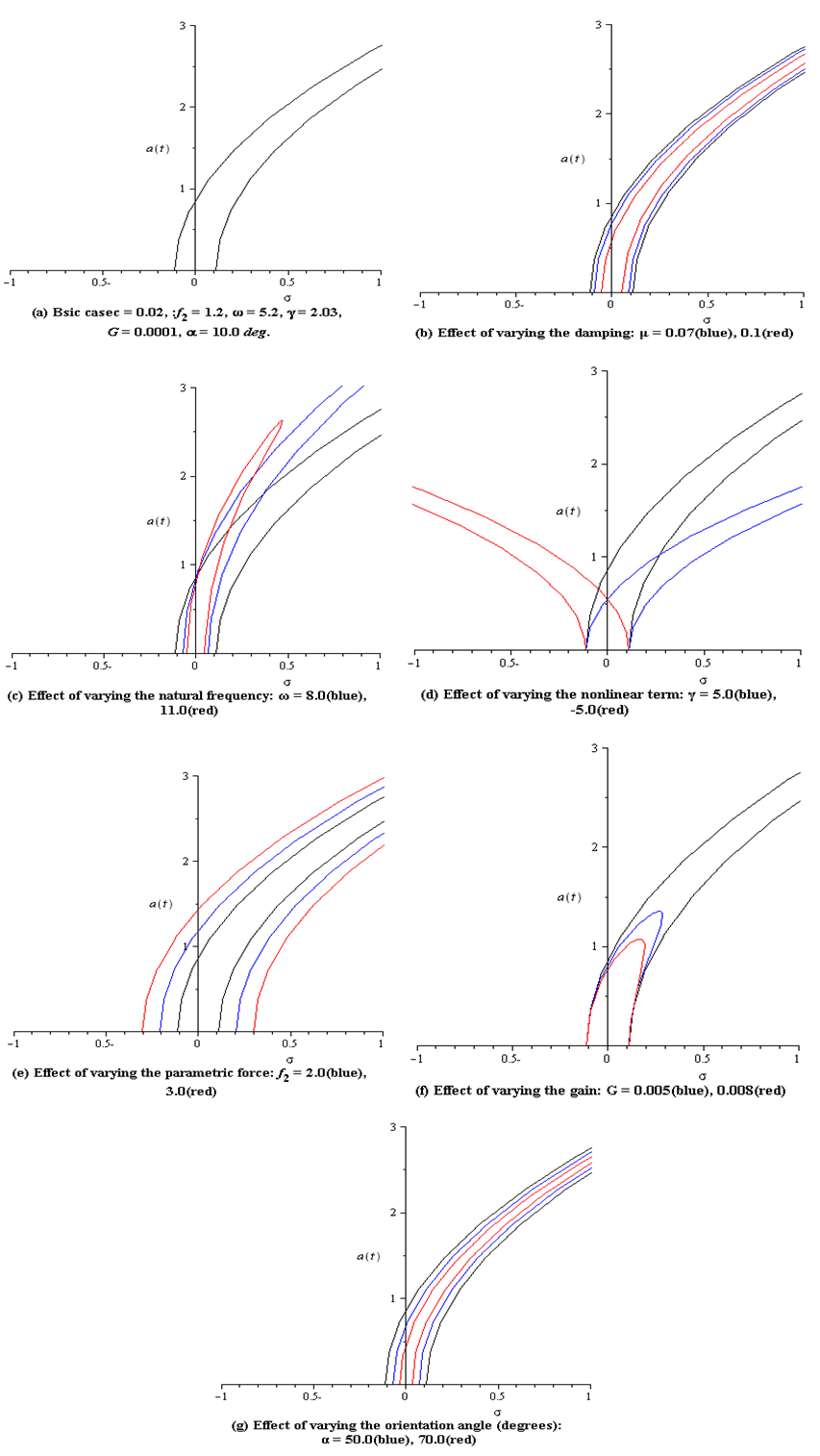 | Figure 9. Principal parametric frequency response curves with CVF controller |
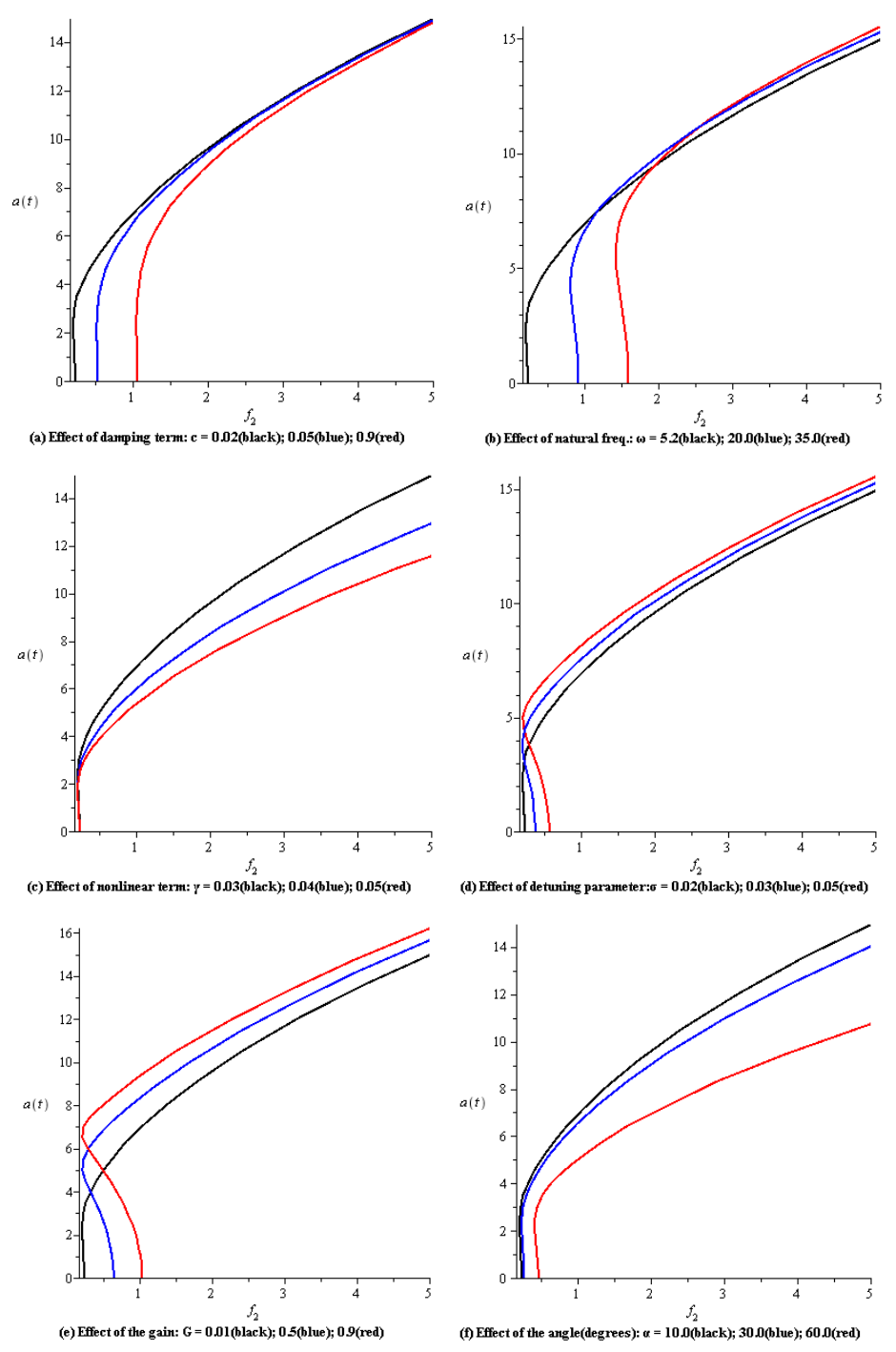 | Figure 10. Principal parametric force response curves with LPF controller |
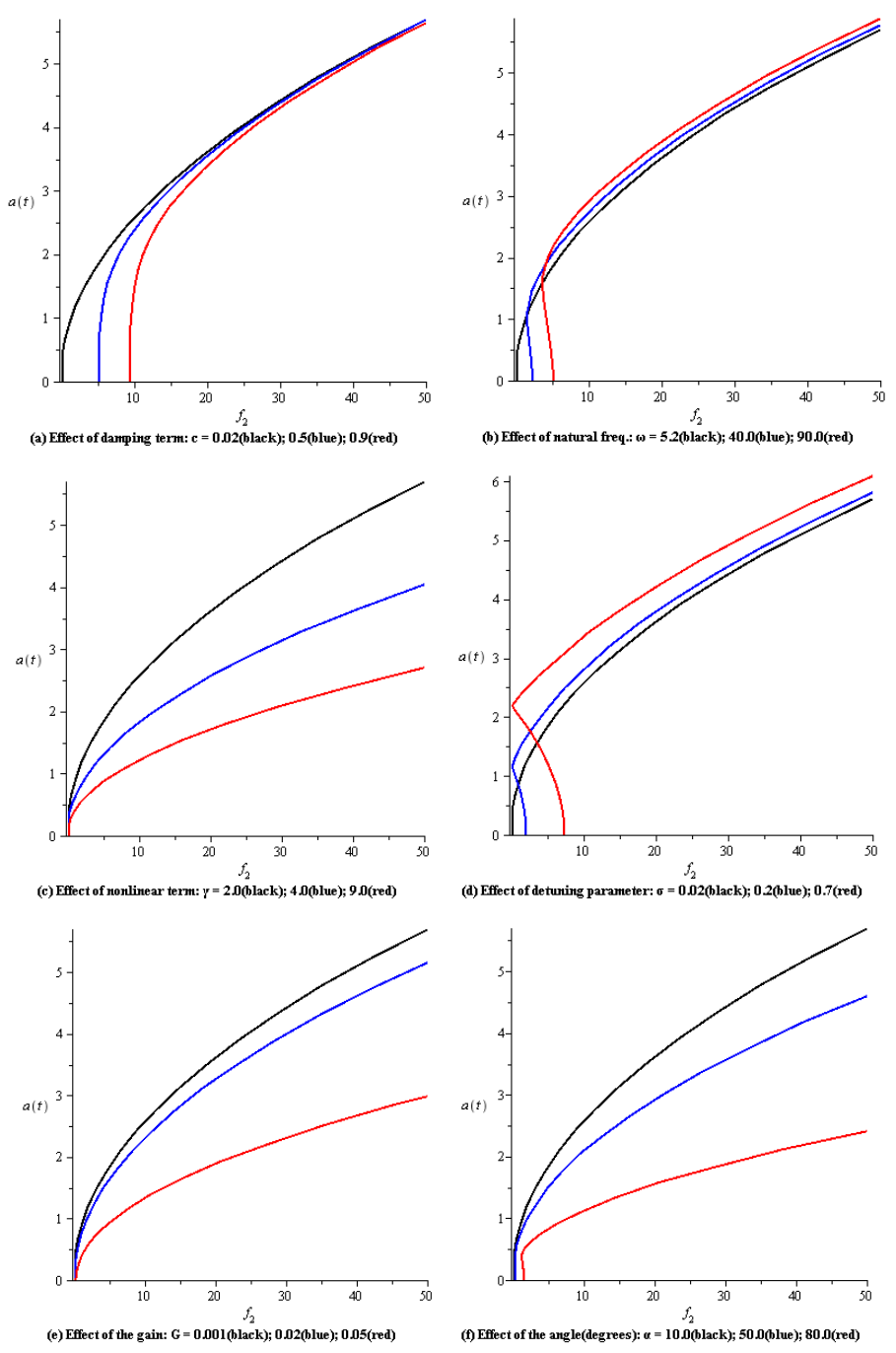 | Figure 11. Principal parametric force response curves with CVF controller |
4.4.1. Frequency-Response Curves
- Table 2 summarizes the effect of system parameters on the frequency response curves and on the steady-state amplitude.Comparing the effects of the system parameters in the numerical solution results, table 1, and in the frequency-response results, table 2, indicates that both results are in a good agreement.
|
4.4.2. Force-Response Curves
- Figures (10) and (11) show the amplitude a as a function of the parametric forcing amplitude f2 with LPF and CVF controls, respectively, as system parameters are varied. It can be seen that magnitude of the steady-state amplitude of the beam is monotonically increasing function in f2.(a) Effect of the damping coefficient µFigures 10(a) and 11(a) indicate that the continuous curves are shifted to the right as µ is increased with decreasing amplitude. The amplitude saturates when f2 > 1.0 and f2 > 10.0 for the force-response curves with LPF and CVF controllers, respectively.(b) Effect the natural frequency ωThe force-response curves in Figs. 10(b) and 11(b) are being shifted to the right as ω increases and the amplitude increases.(c) Effect the cubic nonlinear coefficient γFrom Figs. 10(c) and 11(c), the steady-state amplitude decreases as γ increases. (d) Effect the detuning parameter σIt is noticed that when σ is increased, the continuous curves shift to the right with increasing amplitude and the region of multivaludeness is defined in large intervals, as shown in Figs. 10(d) and 11(d). (e) Effect the gain GFigure 10(e) indicates that the effect of G on the resonant force-response curves with LPF control is similar to the effect of the detuning parameter σ. But the curves with CVF, Fig. 11(e), are shifted downward and the steady-state amplitude decreases significantly as G increases.(f) Effect the orientation angle αIt can be seen from Figs. 10(f) and 11(f) that the steady-state amplitude gets smaller as α increases. Further increase in α lead the continuous curves to be shifted to the right with significant decrease in the amplitude.
5. Conclusions
- The principal parametric vibrations of a varying orientation cantilever beam are investigated and different controllers are proposed to control the periodic and chaotic responses of the first mode of the beam when subjected to external and parametric excitations. The numerical solution is obtained at non-resonant case and principal parametric resonance case under different initial conditions and various control laws. It is found that the nonlinear cantilever beam is sensitive to initial conditions, and the best performance among positive position feedback controllers can be achieved by the LPF one. Whereas the CVF control may perform the best among velocity feedback controllers. The eigenvalues of the corresponding Jacobian matrix are determined to study the stability of the system and the analytic frequency- response curves at resonance. The effect of different parameters is investigated analytically and is verified by numerical simulations. From the study, the following may be concluded.The multivalued solutions appear and the jump phenomenon exists in the subharmonic frequency-response curves with LPF and CVF controllers for all the system parameters. Moreover, the steady-state amplitude is a monotonic decreasing function in the damping coefficient µ, the cubic nonlinear term γ and the orientation angle α. When the natural frequency ω increases, the instability region decreases and the curves are bent to the left. The gain G in the LPF and CVF controls show different effects in the resonant frequency curves, where the continuous frequency curves shift to the left as G in the LPF control increases. But these curves indicate that the steady-state amplitude decreases as G in the CVF is increased. The nonlinearity effect (hardening or softening-type) appears for positive and negative values of the cubic nonlinear parameter γ.From the subharmonic force-response curves with LPF and CVF controllers, it is observed that the steady-state amplitude is a monotonic increasing function in the parametric forcing amplitude f2. The continuous curve of the steady-state amplitude shifts to the right and has (decreasing) or (increasing) stable magnitudes when the values of the parameters (µ, α) or (ω, σ, G of LPF) increase, respectively. The force-response curves shift downwards and the amplitude decreases when the cubic nonlinear parameter γ and the gain G of CVF increase.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML