-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2013; 3(3): 73-80
doi:10.5923/j.control.20130303.01
Identification of Singular Systems under Strong Equivalency
Roja Eini, Abolfazl Ranjbar Noei
Department of Electrical and Computer Engineering, Noushirvani University of Technology, Babol, Iran
Correspondence to: Roja Eini, Department of Electrical and Computer Engineering, Noushirvani University of Technology, Babol, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper modifies parameter identification of singular systems with the aid of transformation of singular system to a new Strong equivalent counterpart. Singular systems should be transformed to an equivalent model in the first step of identification process. In fact choosing an appropriate equivalent singular model is of crucial importance. Inconvenient equivalent model may lead to divergence, excessive computation time and imprecise estimation results. Indeed a more desirable estimation result would be attained by reducing the number of initial conditions. Traditional reduction methods used before for this purpose, but they resulted low accurate estimations because important dynamics of system have been omitted wrongly using those equivalencies. In this paper, a more accurate equivalency transformation of singular systems called Strong equivalency in combination with the Least Square identification algorithm is performed with the aim of revising the mentioned problems. This combination of the Strong equivalency together with the identification procedure is used for the first time. Thus this new configuration improves not only the estimation error convergence, but also the output tracking. Performance of the proposed method is illustrated in a practical singular electric network.
Keywords: Parameter Identification, Singular Systems, Strong Equivalency, Initial Conditions, Reduction Method
Cite this paper: Roja Eini, Abolfazl Ranjbar Noei, Identification of Singular Systems under Strong Equivalency, International Journal of Control Science and Engineering, Vol. 3 No. 3, 2013, pp. 73-80. doi: 10.5923/j.control.20130303.01.
Article Outline
1. Introduction
- Singular systems are widely seen in electrical and electronic networks, mathematics, chemical processes, economic and neural networks and etc. Accordingly an increasing attention has been dedicated to such systems during recent years[1-9]. However singular systems are called by different names according to their various types of applications. They are known as generalized state space systems in the field of control theory and mathematics, descriptor systems in engineering and economics, differential-algebraic equations in numerical analysis and semi-state systems in the electric circuit fields.Singular studies are mainly categorized into two main parts. Actually most of the researches on singular systems are performed during 1960 to 1978. These were involved with the equivalency of differential-algebraic equations and the singular systems theory. Since 1980, the behaviour of such systems has also been investigated typically in control theory.Order reduction techniques and equivalency forms have played an important role in treatment of singular problems in different fields. In fact, usual procedure for dealing with this kind of system is to (either explicitly or implicitly) reduce it to an equivalent regular state space system.Studies on reduction procedure of singular equations were surveyed by Gantmacher in 1959[4]. Then, in 1966 Polak introduced an algorithm to reduce a differential system to a linear time independent state form[10]. In 1969 Fettweis and in 1975, Desoer and Dervisoglu explained a method for reducing the state equation of algebraic - differential systems in circuit theory[11],[12]. In parallel, Luenberger proposed an algorithm for the state equation reduction of singular discrete systems in 1977. Using Shuffle algorithm, a singular discrete system can be changed to an equivalent system regardless of the infinite impulsive modes in the system response[6]. Besides,[13-19] have made great progress in the field of controllability, observability and stability of singular systems.All of the above reports use similar definitions based on regular theory of the reduction technique. In essence, an equivalent system representation based on regular theory keeps most of the original system's dynamics except the infinite impulsive modes. Accordingly neglecting infinite modes is the special problem in these ancient reduction approaches.Indeed Rosenbrock is a pioneer researcher who took the first step in improving the singular equivalency equations by introducing restricted system equivalence (RSE) model based on generalized theory[17]. Although the proposed technique improved the former reduction methods, there were yet some deficiencies involved.However, Strong equivalency model is known as a desired and flexible model for such systems[19]. Regarding this, the aim of this paper is to modify singular system identification by implementing Strong equivalency in it. As a matter of fact, an inappropriate equivalent model for singular identification may lead to divergence, excessive computation and identification with low accuracy. To avoid these difficulties, primarily a new Strong equivalency model on the singular system is employed and then the identification algorithm is used on the equivalent model. In addition identification process is applied on the RSE equivalent model and results of the two methods are compared. Outcome of applying the proposed method is found satisfying in comparison with the previous methods. The verification procedure indicates the effectiveness of the proposed equivalence model in simplifying the complexity of singular identification and improving the difficulties involved with the algebraic equations in these systems. The rest of the paper is organized as follows: in section 2 a general form of a singular system and its problems of identification are described. Section 3 presents singular equivalency approaches and the usual way they are used. Section 4 explains a recursive algorithm of parameter identification. The results of the proposed algorithm and a traditional method are presented through a simulation approach by an illustrative electrical network in section 5. Finally the work is closed by a conclusion in section 6.
2. Problem Formulation
- Consider the following representation form of a linear singular system of order n:
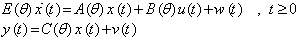 | (1) |
 is the regression parameter vector containing unknown parameters of E, A, B and C. Signals w(t) and v(t) are the process and the system output white Gaussian noises respectively with zero mean and variances of W and V. The target here is to estimate accurately the parameters of system matrices in presence and in free of noise.Considering the singularity of matrix E, impulsive modes usually exist in this type of system. These specific modes cause dependent state space equations. Dependency of the states produce significant troubles meanwhile singular identification process. In fact the initial conditions have to be evaluated by chance in each iteration of the identification algorithm.The usual alternative to meet the identification criteria here is to reduce the number of non zero initial conditions in order to have less dependent equations. Thus a reliable equivalency transformation based on the generalized theory is needed in the first step of singular identification. Secondly identification process can be implemented on the equivalent model.
is the regression parameter vector containing unknown parameters of E, A, B and C. Signals w(t) and v(t) are the process and the system output white Gaussian noises respectively with zero mean and variances of W and V. The target here is to estimate accurately the parameters of system matrices in presence and in free of noise.Considering the singularity of matrix E, impulsive modes usually exist in this type of system. These specific modes cause dependent state space equations. Dependency of the states produce significant troubles meanwhile singular identification process. In fact the initial conditions have to be evaluated by chance in each iteration of the identification algorithm.The usual alternative to meet the identification criteria here is to reduce the number of non zero initial conditions in order to have less dependent equations. Thus a reliable equivalency transformation based on the generalized theory is needed in the first step of singular identification. Secondly identification process can be implemented on the equivalent model. 3. Singular Equivalency
- Singular systems have more complicated form, including not only the finite dynamic modes but also the infinite dynamic and non-dynamic modes. This complication makes singular systems analysis difficult, especially for identification process and the controller design. Singular equivalencies may cope with these difficulties. On the other hand, choosing a sufficient and confident equivalency model relevant to our special work is an important process. Most of the previous works done on singular systems equivalency are mainly based on the regular theory without paying attention to the structural and dynamical characteristics of equation (1). In fact, those methods are based on transforming the original singular system in (1) to the following state space system of order
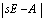 . The methods are called order reduction methods. See[4],[10] for further information.
. The methods are called order reduction methods. See[4],[10] for further information.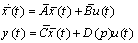 | (2) |
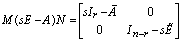 | (3) |
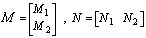 | (4) |
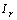 and
and 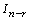 have r and n-r dimensions respectively, n is the system regular degree of freedom and
have r and n-r dimensions respectively, n is the system regular degree of freedom and 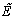 is the nilpotent matrix with k=n-r index which is equal to singular system index. Vector of state variables can be divided into two following sub vectors:
is the nilpotent matrix with k=n-r index which is equal to singular system index. Vector of state variables can be divided into two following sub vectors: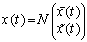 | (5) |
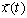 and
and 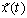 are regular and singular subsystem state vectors respectively. System (1) can be written in the following Laplace form:
are regular and singular subsystem state vectors respectively. System (1) can be written in the following Laplace form: 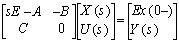 | (6) |
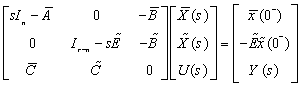 | (7) |
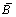 and
and 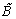 denote appropriate sub blocks of MB. Similarly
denote appropriate sub blocks of MB. Similarly 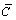 and
and 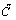 are sub blocks of CN. This transformation divides the original system into two subsystems. Accordingly important properties of system behaviour at infinity will be preserved. As a result, behaviour of x in the original system will be similar to the state variables behaviour of the RSE system.Although this approach has superiority over the conventional reduction techniques, there are still some shortcomings. This is due to considering some of unnecessary restrictions on the algebraic subsystem. On the other hand, the two subsystems' parameters should be estimated separately and this produces inaccuracy in identification process.A kind of Strong equivalency is used including extra constraints over the Rosenbrock equivalency procedure to overcome the mentioned difficulties. Equation (6) can be stated here as equation (8) under the Strong equivalency.
are sub blocks of CN. This transformation divides the original system into two subsystems. Accordingly important properties of system behaviour at infinity will be preserved. As a result, behaviour of x in the original system will be similar to the state variables behaviour of the RSE system.Although this approach has superiority over the conventional reduction techniques, there are still some shortcomings. This is due to considering some of unnecessary restrictions on the algebraic subsystem. On the other hand, the two subsystems' parameters should be estimated separately and this produces inaccuracy in identification process.A kind of Strong equivalency is used including extra constraints over the Rosenbrock equivalency procedure to overcome the mentioned difficulties. Equation (6) can be stated here as equation (8) under the Strong equivalency.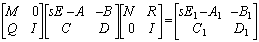 | (8) |
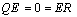 . The constraints here are on R and Q matrices. Therefore two systems
. The constraints here are on R and Q matrices. Therefore two systems 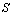 and
and 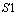 are Strong equivalent if and only if standard forms for them are related by Strong operation as in (8). In addition this should be considered that finding appropriate matrices in this approach is innovative and varies depending on the type of singularity problem.It can be clearly seen that the Strong equivalency provide one integrated system rather than two separate sub-systems in RSE model. So system can be identified more easily and precisely with the aid of Strong equivalency. On the other hand the Strong model reflects the original systems' information better. Experiments indicated that this equivalencytransformation is more reliable and effective for identification process than others[19]; therefore this model is employed in this paper in combination with identification algorithm to identify singular system parameters.
are Strong equivalent if and only if standard forms for them are related by Strong operation as in (8). In addition this should be considered that finding appropriate matrices in this approach is innovative and varies depending on the type of singularity problem.It can be clearly seen that the Strong equivalency provide one integrated system rather than two separate sub-systems in RSE model. So system can be identified more easily and precisely with the aid of Strong equivalency. On the other hand the Strong model reflects the original systems' information better. Experiments indicated that this equivalencytransformation is more reliable and effective for identification process than others[19]; therefore this model is employed in this paper in combination with identification algorithm to identify singular system parameters. 4. Identification Algorithm
- Recursive Least Square (RLS) algorithm is applied in this case due to its efficiency in parameter identification.Considering equation (8) and (7), the objective here is to identify equivalent system parameters through the following procedure which is summarized in three steps of: 1. Update unknown vector of parameters by:
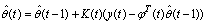 | (9) |
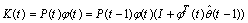 | (10) |
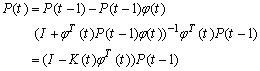 | (11) |
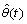 denotes the parameter vector containing estimated values at time t.
denotes the parameter vector containing estimated values at time t. 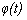 is the regression vector,
is the regression vector, 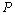 and
and 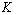 are covariance and gain matrices, respectively.
are covariance and gain matrices, respectively. 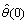 ,
, 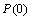 and number of iterations must be initially defined as initial conditions.
and number of iterations must be initially defined as initial conditions. 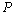 ,
, 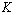 and
and 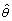 will be repeatedly updated in each iteration until the estimated parameters converge to the real values via a stopping criteria.According to the first stage of the algorithm, output y(t) value is needed in each iteration. Output of the system depends on the state variables as well. Therefore initial conditions of the states are required during the process. So inappropriate equivalent model may cause divergence from the real results which may be ensued by excessive time consumption as it happened in identification on RSE model. In contrary outcomes of identification algorithm on the proposed equivalent model are satisfactory and very close to the real parameters of the original system.
will be repeatedly updated in each iteration until the estimated parameters converge to the real values via a stopping criteria.According to the first stage of the algorithm, output y(t) value is needed in each iteration. Output of the system depends on the state variables as well. Therefore initial conditions of the states are required during the process. So inappropriate equivalent model may cause divergence from the real results which may be ensued by excessive time consumption as it happened in identification on RSE model. In contrary outcomes of identification algorithm on the proposed equivalent model are satisfactory and very close to the real parameters of the original system.5. Simulation Results
5.1. Equivalency Results
- A practical LCR circuit as shown in Fig. 1[20],[21] is transformed to its RSE and Strong equivalent model.The following equations can be attained using KVL and KCL laws.
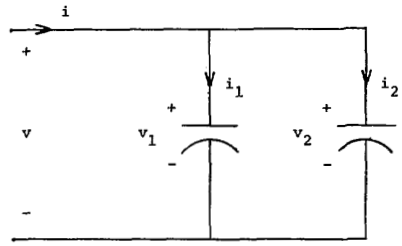 | Figure 1. A practical LCR circuit in parameter identification |
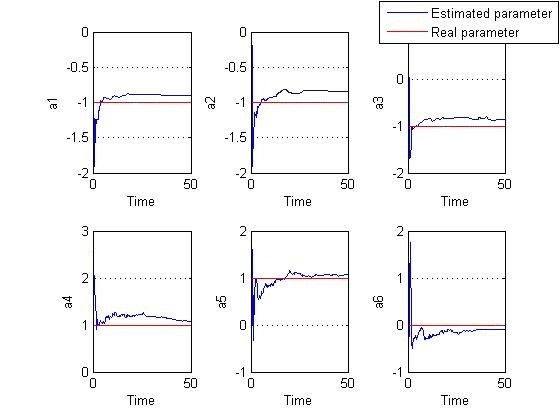 | Figure 2. Estimated and real parameters-identification on RSE- without noise |
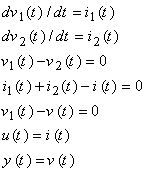 | (12) |
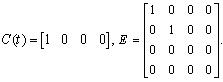 | (13) |
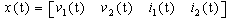 | (14) |
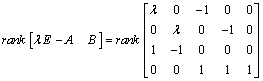 | (15) |
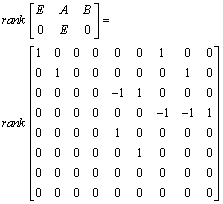 | (16) |
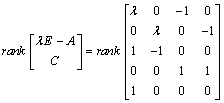 | (17) |
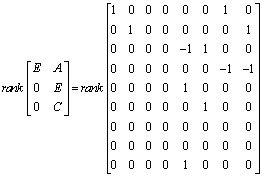 | (18) |
5.1.1. Restricted System Equivalency (RSE) Result
- Here, the original system is transformed to its RSE equivalent model to recognize the effectiveness of the proposed model more obviously.From equation (6), the original system of (13) can be transformed to the following model with state variables of equation (14):
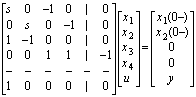 | (19) |
 and unknown matrices of
and unknown matrices of  .
.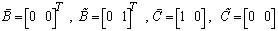
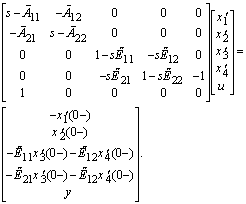 | (20) |
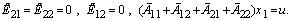 and
and 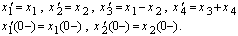 | (21) |
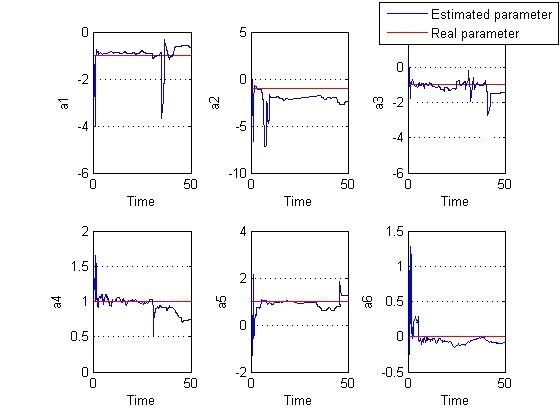 | Figure 3. Estimated and real parameters- identification on RSE- without noise |
5.1.2. Strong Equivalency Result
- As a contribution the following Strong equivalency is employed in this section. Indeed this is inspired form the system analysis. Equation (12) can be manipulated to:
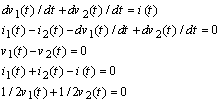 | (22) |
 ,
,  ,
, 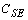 and
and 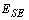 matrices are defined as:
matrices are defined as: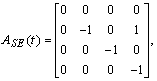
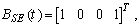
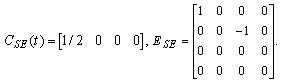 | (23) |
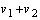 ,
,  ,
, 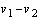 and
and 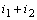 . Input and output of the new system are kept the same as the original system. By this transformation the initial conditions of the two state variables
. Input and output of the new system are kept the same as the original system. By this transformation the initial conditions of the two state variables 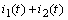 and
and 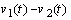 exactly become zero. This is an advantage of the proposed equivalency for accurate singular identification in purpose of representing the system just by input-output data. This is because input-output data of the system is mainly used in the identification process.
exactly become zero. This is an advantage of the proposed equivalency for accurate singular identification in purpose of representing the system just by input-output data. This is because input-output data of the system is mainly used in the identification process.5.2. Singular Identification Result
- In the second step RLS identification is applied on the two equivalent models of previous section.
5.2.1. Identification on RSE Model
- In this case, covariance matrix P(0) is initially chosen as
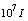 . The two figures are resulted with and without v(t) and w(t) noises respectively. V and W variances are selected as 0.9. Besides the process is time consuming the final value of the parameters had not arrived at its optimum point. In addition initial conditions are chosen so that divergence does not occur. However it surely happens through an identification of a more complicated singular system.From Figure 3, noise trace can be completely observed and the final values are not admissible.
. The two figures are resulted with and without v(t) and w(t) noises respectively. V and W variances are selected as 0.9. Besides the process is time consuming the final value of the parameters had not arrived at its optimum point. In addition initial conditions are chosen so that divergence does not occur. However it surely happens through an identification of a more complicated singular system.From Figure 3, noise trace can be completely observed and the final values are not admissible. 5.2.2. Identification on Strong Equivalent Model
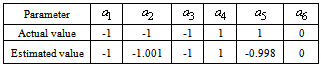
- Parameters of the Strong equivalent model in (23) are estimated by RLS algorithm as well. 500 input output samples are used in this algorithm and the initial estimates for the parameters are taken as zero (a possible assumption according to the Strong equivalency). The covariance matrix P(0) is initially chosen as
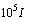 with appropriate dimensions.
with appropriate dimensions.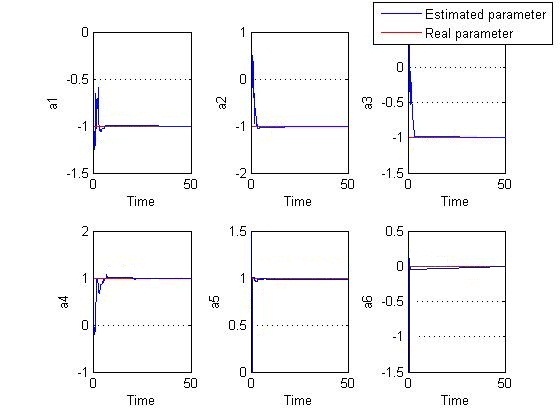 | Figure 4. Estimated and real parameters-identification on Strong equivalency- without noise |
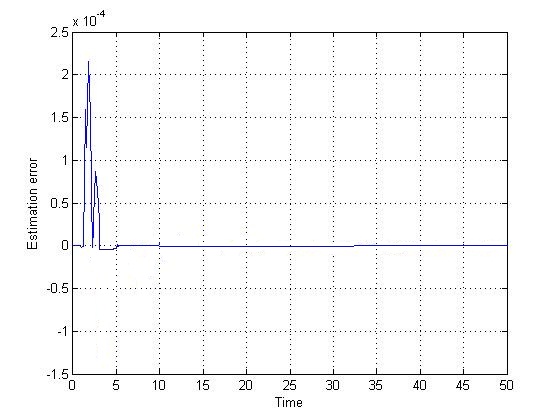 | Figure 5. Estimation error- identification on Strong equivalency-without noise |
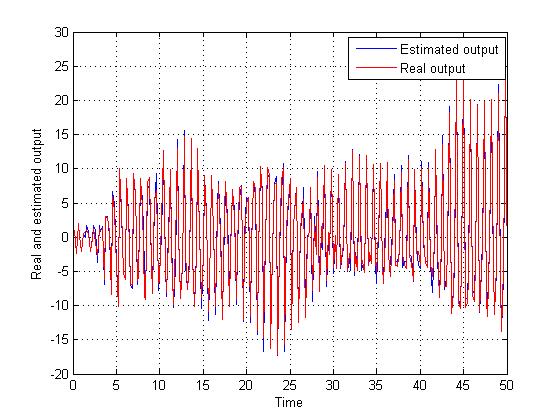 | Figure 6. Output tracking- identification on Strong equivalency-without noise |
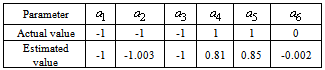
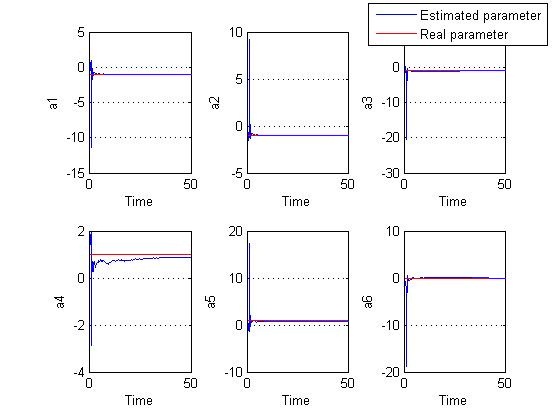 | Figure 7. Estimated and real parameters-identification on Strong equivalency with noise |
|
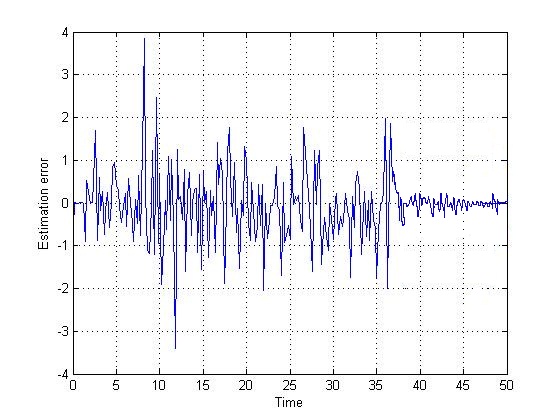 | Figure 8. Estimation error-identification on Strong equivalency- with noise |
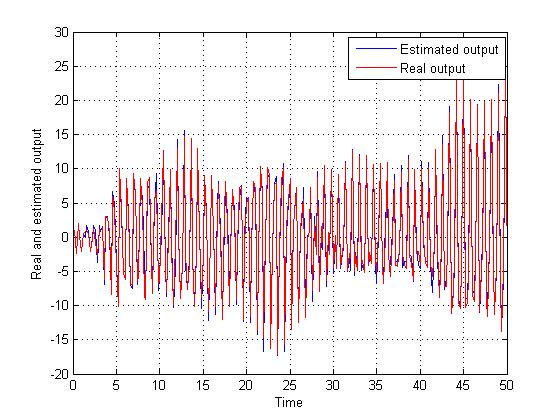 | Figure 9. Output tracking- identification on Strong equivalency-with noise |
|
6. Conclusions
- An identification technique is implemented in this paper to identify singular systems. Furthermore an appropriate singular equivalency is proposed within the identification algorithm.The proposed equivalency method is based on restricted system equivalency (RSE) with extra constraints, which provide more accurate equivalent model with fewer initial conditions. Thus, the convergence speed of the identification process is improved in comparison with the previous approach. Significance of the proposed equivalency in combination with the identification algorithm is shown through a simulation study on a 2nd order circuit. It is seen that estimated values are finally converged to the actual original parameters with fewer estimation error even in presence of white Gaussian noise. The proposed approach also needs less information about the initial values due to transformation of system states to new equivalent states. This new form guarantees the convergence of the identification algorithm by transforming the state variables with zero initial conditions. Simulation results from the new and the traditional methods signify the performance of the proposed equivalency technique in combination with the identification procedure.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML