| [1] | N. M. Krylov and N. N. Bogoliubov, Introduction to Nonlinear Mechanics. Princeton, USA: Princeton University Press, 1947. |
| [2] | N. N. Bogoliubov and Yu. A. Mitropolsky, Asymptotic Methods in the Theory of Non-Linear Oscillations. New York, USA: Gordon and Breach, 1961. |
| [3] | Th. J. Coakley, AGeneralized Averaging Method for Linear Differential Equations with Almost Periodic Coefficients. Washington, USA:National Aeronautics and Space Administration, D. C., 1969. |
| [4] | Ju. A. Mitropolsky, Method of an Average in the Nonlinear Mechanics. Kiev, USSR:Naukovadumka, 1971, (Russian). |
| [5] | A. Sanders and F. Verhulst, Averaging Methods in Nonlinear Dynamical Systems. Appl. Math. Sci., New York, USA: Springer-Verlag, 1985, vol. 59. |
| [6] | V. M. Volosov and B. I. Morgunov, Metod of Average in the Theory of Nonlinear Oscillations. Мoscow, USSR: Moscow State University Publishing house, 1971, (Russian). |
| [7] | P. Lochak, C. Meunier, Multiphase Averaging for Classical Systems. Appl. Math. Sci., New York, USA:Springer-Verlag, 1988, vol. 72. |
| [8] | N. A. Perestyuk, V. A. Plotnikov, A. M. Samoilenko and N. V. Skripnik, Differential Equations with Impulse Effects: Multivalued Right-Hand Sides with Discontinuities. De Gruyter Studies in Mathematics. Berlin/Boston: Walter De GruyterGmbH&Co., 2011, vol. 40. |
| [9] | A. V. Plotnikov and N. V. Skripnik, Differential Equations with ''Clear'' and Fuzzy Multivalued Right-Hand Sides. Asymptotics Methods. Odessa, Ukraine:AstroPrint, 2009, (Russian). |
| [10] | Klymchuk, S., Plotnikov, A., and Skripnik, N., 2012, Overview of V.A. Plotnikov’s research on averaging of differential inclusions.,Physica D: Nonlinear Phenomena, 241(22), 1932-1947. doi:10.1016/j.physd.2011.05.004. |
| [11] | V. A. Plotnikov, A. V. Plotnikov and A. N. Vityuk, Differential Equations with a Multivalued Right-Hand Side: Asymptotic methods. Odessa, Ukraine: AstroPrint, 1999, (Russian). |
| [12] | Zadeh, L. A., 1965, Fuzzy sets., Inf. Control, (8), 338-353, doi:10.1016/S0019-9958(65)90241-X. |
| [13] | Kwun, Y. C., Kim, M. J., Lee, B. Y., and Park, J. H., 2008, Existence of solutions for the semilinear fuzzy integrodifferential equations using by successive iteration., Journal of Korean Institute of Intelligent Systems, 18, 543-548, doi:10.5391/JKIIS.2008.18.4.543. |
| [14] | Kwun, Y. C., Kim, J. S., Park, M. J., and Park, J. H., 2009, Nonlocal controllability for the semilinear fuzzy integrodifferential equations in n-dimensional fuzzy vector space., Adv. Difference Equ., vol. 2009, Article ID 734090, 16 pages, doi:10.1155/2009/734090. |
| [15] | Kwun, Y. C., Kim, J. S., Park, M. J., and Park, J. H., 2010, Controllability for the impulsive semilinear nonlocal fuzzy integrodifferential equations in n-dimensional fuzzy vector space., Adv. Difference Equ., vol. 2010, Article ID 983483, 22 pages, doi:10.1155/2010/983483. |
| [16] | Park, J. H., Park, J. S., and Kwun, Y. C., 2006, Controllability for the semilinear fuzzy integrodifferential equations with nonlocal conditions., Fuzzy Systems and Knowledge Discovery, Lecture Notes in Computer Science, vol. 4223/2006, 221-230, doi: 10.1007/11881599_25. |
| [17] | Park, J. H., Park, J. S., Ahn, Y. C., and Kwun, Y. C., 2007, Controllability for the impulsive semilinear fuzzy integrodifferential equations., Adv. Soft Comput., 40, 704-713, doi:10.1007/978-3-540-71441-5_76. |
| [18] | Vasil'kovskaya, V. S., and Plotnikov, A. V., 2007, Integrodifferential systems with fuzzy noise.,Ukr. Math. J., 59(10), 1482-1492, doi:10.1007/s11253-008-0005-z. |
| [19] | Plotnikov, A. V., 2011, Averaging of fuzzy integrodifferential inclusions., International Journal of Control Science and Engineering, 1(1),8-14,doi:10.5923/j.control.20110101.02. |
| [20] | Puri, M. L., and Ralescu, D. A., 1986, Fuzzy random variables., J. Math. Anal. Appl., 114(2), 409-422, doi:10.1016/0022-247X(86)90093-4. |
| [21] | Park, J. Y., and Han, H. K., 1999, Existence and uniqueness theorem for a solution of fuzzy differential equations., Int. J. Math. Math. Sci., 22(2), 271-279, doi:10.1155/S016117129 9222715. |
| [22] | Aubin, J.-P., 1990, Fuzzy differential inclusions.,Probl. Control Inf. Theory, 19(1), 55-67. |
| [23] | Baidosov, V. A., 1990, Differential inclusions with fuzzy right-hand side.,Sov. Math., 40(3), 567-569. |
| [24] | Baidosov, V. A., 1990, Fuzzy differential inclusions., J. Appl. Math. Mech., 54(1), 8-13, doi:10.1016/0021- 8928(90)90080 -T. |
| [25] | Hullermeier, E., 1997, An approach to modeling and simulation of uncertain dynamical system., Int. J. Uncertain. Fuzziness Knowl.-Based Syst., 7, 117-137. |
| [26] | E. B. Lee and L. Markus, Foundations of Optimal Control Theory. New York, London, Sydney:John Wiley & Sons, Inc.,1967. |
| [27] | G. V. Smirnov, Introduction to the Theory of Differential Inclusions. Graduate Studies in Mathematics. Providence, Rhode Island, USA:American Mathematical Society, 2002, vol. 41. |
| [28] | Plotnikov, A.V., 1990, Asymptotic investigation of equations of controlled motion with multivalued trajectories.,Ukr. Math. J. 42(10), 1251-1254, doi: 10.1007/BF01057399. |
| [29] | Plotnikov, A.V., 2000, Averaging of equations of a controlled motion with a multivalued control criterion., Nonlinear Oscillatons.3(4), 505-510, (Russian). |

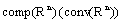 be a set of all nonempty (convex) compact subsets from the space
be a set of all nonempty (convex) compact subsets from the space 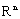 ,
,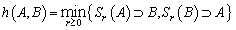 beHausdorff distance between sets
beHausdorff distance between sets 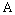 and
and 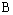 ,
, 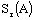 is
is 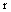 -neighborhood of set
-neighborhood of set 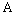 .Let
.Let 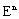 be the set of all
be the set of all 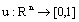 such that u satisfies the following conditions:1)
such that u satisfies the following conditions:1) 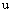 is normal, that is, there exists an
is normal, that is, there exists an 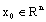 such that
such that 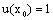 ;2)
;2) 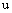 is fuzzy convex, that is,
is fuzzy convex, that is, 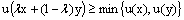 for any
for any 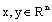 and
and 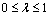 ;3)
;3) 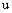 is upper semicontinuous;4)
is upper semicontinuous;4) 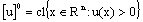 is compact.If
is compact.If 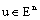 , then
, then 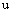 is called a fuzzy number, and
is called a fuzzy number, and 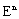 is said to be a fuzzy number space. For
is said to be a fuzzy number space. For 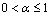 , denote
, denote 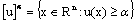 .Then from 1)-4), it follows that the
.Then from 1)-4), it follows that the 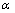 -level set
-level set 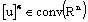 for all
for all 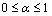 .Let
.Let 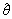 be the fuzzy mapping defined by
be the fuzzy mapping defined by 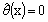 if
if 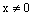 and
and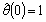 .Define
.Define 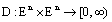 by the relation
by the relation 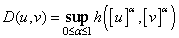 ,where
,where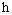 is the Hausdorff metric defined in
is the Hausdorff metric defined in 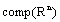 . Then
. Then 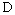 is a metric in
is a metric in 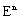 .Further we know that[20]:1)
.Further we know that[20]:1) 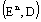 is a complete metric space,2)
is a complete metric space,2) 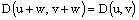 for all
for all 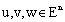 ,3)
,3) 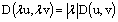 for all
for all 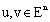 and
and 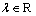 .Definition 1.[21] A fuzzy mapping
.Definition 1.[21] A fuzzy mapping 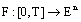 is measurable if for all
is measurable if for all 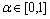 the set-valued map
the set-valued map 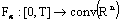 defined by
defined by 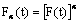 is Lebesgue measurable.Definition 2.[21] A fuzzy mapping
is Lebesgue measurable.Definition 2.[21] A fuzzy mapping 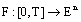 is said to be integrably bounded if there is an integrable function
is said to be integrably bounded if there is an integrable function 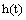 such that
such that 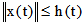 for every
for every 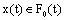 .Definition 3.[21] The integralofafuzzy mapping
.Definition 3.[21] The integralofafuzzy mapping 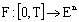 isdefinedlevelwiseby
isdefinedlevelwiseby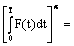
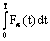 .The set
.The set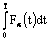 of all
of all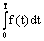 such that
such that 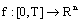 is a measurable selection for
is a measurable selection for 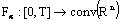 for all
for all 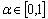 .Definition 4.[21] A measurable and integrably bounded fuzzy mapping
.Definition 4.[21] A measurable and integrably bounded fuzzy mapping 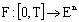 is said to be integrable over
is said to be integrable over 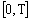 if
if 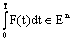 . Note that if
. Note that if 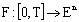 is measurable and integrably bounded, then is integrable. Further if
is measurable and integrably bounded, then is integrable. Further if 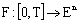 is continuous, then it is integrable.Now we consider following fuzzy integrodifferential inclusion
is continuous, then it is integrable.Now we consider following fuzzy integrodifferential inclusion 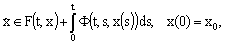
 means
means ;
;  is the state;
is the state; 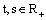 ;
;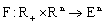 is a fuzzy mapping;
is a fuzzy mapping; 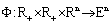 is a fuzzy mapping;
is a fuzzy mapping; 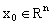 . We interpret[22-25] the fuzzy integrodifferential inclusion (1) as a family of integrodifferential inclusions
. We interpret[22-25] the fuzzy integrodifferential inclusion (1) as a family of integrodifferential inclusions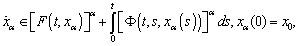
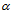 indicates that the
indicates that the 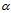 -level set of a fuzzy set is involved (the system (2) can only have any significance as a replacement for (1) if the solutions generate fuzzy sets (fuzzy R-solution)[25]).Let
-level set of a fuzzy set is involved (the system (2) can only have any significance as a replacement for (1) if the solutions generate fuzzy sets (fuzzy R-solution)[25]).Let 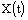 denotes the fuzzy R-solution of the fuzzy integrodifferential inclusion (1).Now we consider following control integrodifferential equations with the fuzzy parameter
denotes the fuzzy R-solution of the fuzzy integrodifferential inclusion (1).Now we consider following control integrodifferential equations with the fuzzy parameter 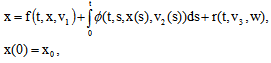
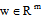 is the control;
is the control; 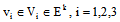 are fuzzy parameters;
are fuzzy parameters; 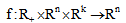 ,
, 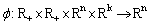 ,
, 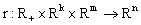 .Definition 5. The set
.Definition 5. The set 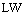 of all measurable single-valued branches of the set
of all measurable single-valued branches of the set 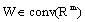 is the set of the admissible controls.Further we consider following control fuzzy integrodifferential inclusions
is the set of the admissible controls.Further we consider following control fuzzy integrodifferential inclusions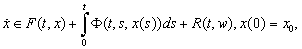
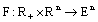 ,
, 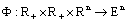 ,
, 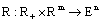 are fuzzy maps such that
are fuzzy maps such that 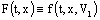 ,
, 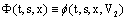 ,
, 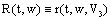 .Obviously, the control fuzzy integrodifferential inclusion (4) turns into the ordinary fuzzy integrodifferential inclusion
.Obviously, the control fuzzy integrodifferential inclusion (4) turns into the ordinary fuzzy integrodifferential inclusion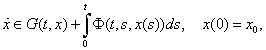
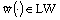 is fixed and
is fixed and 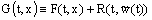 .Let
.Let 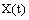 denotes the fuzzy R-solution of the fuzzy integrodifferential inclusion (5), then
denotes the fuzzy R-solution of the fuzzy integrodifferential inclusion (5), then 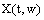 denotes the fuzzy R-solution of the control fuzzy integrodifferential inclusion (4) for the fixed
denotes the fuzzy R-solution of the control fuzzy integrodifferential inclusion (4) for the fixed 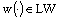 .Definition 6.The set
.Definition 6.The set 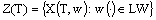 be called the attainable set of the fuzzy system (4).
be called the attainable set of the fuzzy system (4).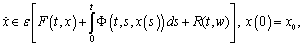
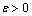 is a small parameter. In this section we associate with the equation (6) the following averaged integrodifferential equation
is a small parameter. In this section we associate with the equation (6) the following averaged integrodifferential equation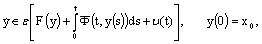
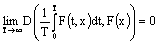
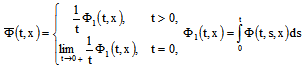
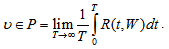
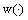 of the initial inclusion (6) and by the control
of the initial inclusion (6) and by the control 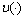 of averaged inclusion (7).We will put the control
of averaged inclusion (7).We will put the control 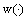 in correspondence a control
in correspondence a control 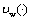 as it follows:1) We calculate
as it follows:1) We calculate 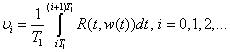 ,where
,where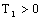 is constant.2) Now we build the control
is constant.2) Now we build the control 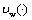 as it follows:
as it follows: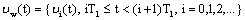 ,where
,where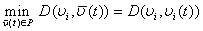 .We will put the control
.We will put the control 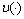 in correspondence a control
in correspondence a control 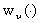 as it follows:1) We calculate
as it follows:1) We calculate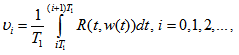 ,where
,where 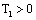 is constant.2) Now we build the control
is constant.2) Now we build the control 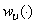 as it follows:
as it follows: 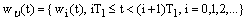 ,where
,where 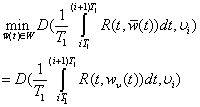 Now we consider Mayer fuzzy problem.As is generally known, the Mayer problem, is to maximize, over all solutions to control system defined on fixed time interval, a functional depending on the final position[26,27]. Mayer fuzzy problem: let
Now we consider Mayer fuzzy problem.As is generally known, the Mayer problem, is to maximize, over all solutions to control system defined on fixed time interval, a functional depending on the final position[26,27]. Mayer fuzzy problem: let 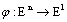 be a continuous fuzzy map and
be a continuous fuzzy map and 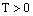 . For example
. For example 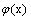 such that
such that 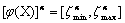 forall
forall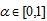 ,where
,where 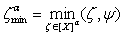 ,
, 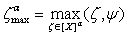 is constant,
is constant,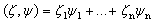 .Definition 6.An admissible control
.Definition 6.An admissible control 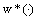 is said to be an optimal control for problem (6) if
is said to be an optimal control for problem (6) if 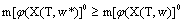
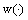 , where
, where 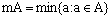 ,
, 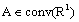 . Now we obtain the main result of this article.Theorem. Let in domain
. Now we obtain the main result of this article.Theorem. Let in domain 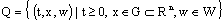 the following hold:1)
the following hold:1) 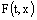 is continuous in
is continuous in 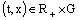 ;2)
;2) 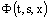 is continuous in
is continuous in 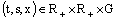 ;3) there exist constants
;3) there exist constants 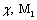 such that
such that 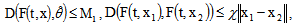 for all
for all 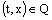 , and any
, and any 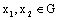 ;4) there exist continuous functions
;4) there exist continuous functions 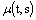 ,
, 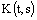 , and constant
, and constant 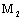 such that
such that 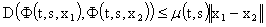 ,
, 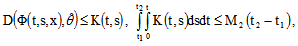 for any
for any 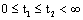 , and any
, and any 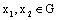 ;5) there exist constants
;5) there exist constants 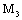 , and
, and 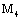 such that
such that 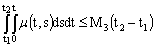 ,
,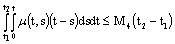 ,for any
,for any 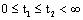 ;6) there exist continuous functions
;6) there exist continuous functions 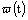 ,
, 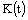 , and constants
, and constants 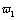 ,
, 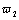 ,
, 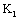 such that
such that 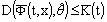 ,
, 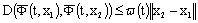 ,
,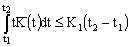 ,
, 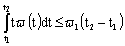 ,
,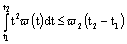 ,for any
,for any 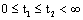 and
and 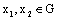 ;7) the limits (8),(9) exist uniformly in
;7) the limits (8),(9) exist uniformly in 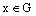 ;8)
;8) 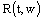 is continuous in
is continuous in 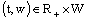 ;9) there exists constant
;9) there exists constant 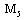 such that
such that 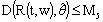 for all
for all 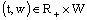 ;10) the limit (10) exists;11) for any
;10) the limit (10) exists;11) for any 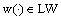 and
and 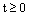 the fuzzy R-solution of the system (7) together with a
the fuzzy R-solution of the system (7) together with a 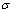 -neighbourhood belong to the domain
-neighbourhood belong to the domain 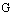 , i.e.
, i.e. 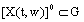 ;12) there exists a constant
;12) there exists a constant 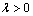 such that
such that 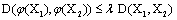 for all
for all 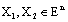 ; Then for any
; Then for any 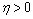 and
and 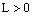 there exists
there exists 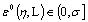 such that for all
such that for all 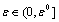 and
and 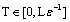 the following statements hold:a) for an optimal control
the following statements hold:a) for an optimal control 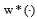 of Mayer fuzzy problem (6) there exists an admissible control
of Mayer fuzzy problem (6) there exists an admissible control 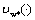 of the fuzzy system (7) such that
of the fuzzy system (7) such that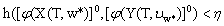
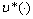 of Mayer fuzzy problem (7) there exists an admissible control
of Mayer fuzzy problem (7) there exists an admissible control 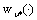 of the fuzzy system (6) such that
of the fuzzy system (6) such that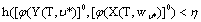
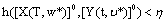
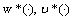 are an optimal control of Mayer fuzzy problems (6) and (7);Proof. Let
are an optimal control of Mayer fuzzy problems (6) and (7);Proof. Let 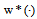 and
and 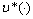 are optimal controls of Mayer fuzzy problems (6) and (7).Let
are optimal controls of Mayer fuzzy problems (6) and (7).Let 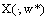 and
and 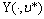 are fuzzy R-solutions of following fuzzy systems
are fuzzy R-solutions of following fuzzy systems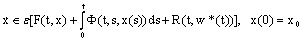 ,
,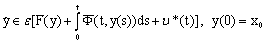 .Let
.Let 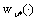 is an admissible control of the fuzzy system (7) corresponding to the optimal control of
is an admissible control of the fuzzy system (7) corresponding to the optimal control of 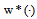 , and
, and 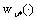 is an admissible control of the fuzzy system (6) corresponding to the optimal control of
is an admissible control of the fuzzy system (6) corresponding to the optimal control of 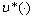 .Let
.Let 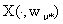 and
and 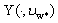 are fuzzy R-solutions of following fuzzy systems
are fuzzy R-solutions of following fuzzy systems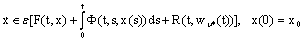 ,
,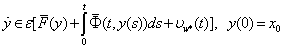 .By conditions 1)-12) and[44] so that
.By conditions 1)-12) and[44] so that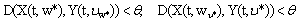 for all
for all 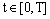 .Then we get
.Then we get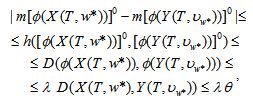
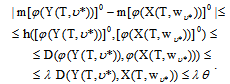
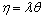 then we obtain (15) and (16).Since
then we obtain (15) and (16).Since 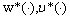 are optimal controls of Mayer fuzzy problems (6) and (7), and
are optimal controls of Mayer fuzzy problems (6) and (7), and 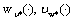 areadmissible controls of the fuzzy systems (6) and (7), we have
areadmissible controls of the fuzzy systems (6) and (7), we have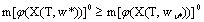 ,
,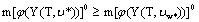 .Also, we obviously have
.Also, we obviously have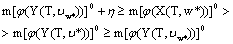 or
or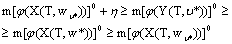 Hence, we obtain (12) - (14). The theorem is proved. Remark.If we replace (11) on
Hence, we obtain (12) - (14). The theorem is proved. Remark.If we replace (11) on 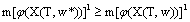 or
or 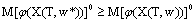 or
or 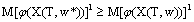 ,where
,where 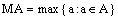 ,
, 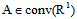 , then a theorem will be just.
, then a theorem will be just.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML