Jose Manuel Lopez-Guede1, Borja Fernandez-Gauna2, Manuel Graña3, Fernado Oterino4
1Dept. of Systems Engineering and Automatic Control, University College of Engineering of Vitoria, Basque Country University (UPV/EHU), Vitoria, 01006, Spain
2Dept. of Software and Computing Systems, University College of Engineering of Vitoria, Basque Country University (UPV/EHU), Vitoria, 01006, Spain
3Dept. of Computer Science and Artificial Intelligence, Faculty of Informatics, Basque Country University (UPV/EHU), San Sebastian, 20018, Spain
4Dept. of Electronics, University College of Engineering of Vitoria, Basque Country University (UPV/EHU), Vitoria, 01006, Spain
Correspondence to: Jose Manuel Lopez-Guede, Dept. of Systems Engineering and Automatic Control, University College of Engineering of Vitoria, Basque Country University (UPV/EHU), Vitoria, 01006, Spain.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper authors propose to study the influence of the prediction horizon on Dynamic Matrix Control (DMC). This kind of controllers is a particular type of Model Predictive Control (MPC), which are framed as advanced controllers. To follow a scientific procedure and to objectify such influence, authors have taken into consideration a set of indexes defined to measure the performance reached at the output of a system when it is controlled by different DMC controllers, which have been synthesized varying in a planned and systematic way the value of the prediction horizon. The system on which the influence of the parameter has been analysed has been chosen because it has shown to be difficult to control using classical control schemes, as a discretized Proportional Integral Derivative (PID) control tuned by means of the Ziegler-Nichols method. In this study 720 different experiments have been carried out, and the effect of the prediction horizon parameter is summarized by means a number of figures.
Keywords:
Model Predictive Control, Dynamic Matrix Control, Prediction Horizon
Cite this paper: Jose Manuel Lopez-Guede, Borja Fernandez-Gauna, Manuel Graña, Fernado Oterino, On the Influence of the Prediction Horizon in Dynamic Matrix Control, International Journal of Control Science and Engineering, Vol. 3 No. 1, 2013, pp. 22-30. doi: 10.5923/j.control.20130301.03.
1. Introduction
Dynamic Matrix Control (DMC) is a concrete type of Model Predictive Control (MPC), which is a set of advanced control schemas, i.e., they are more advanced than Proportional Integral Derivative (PID) controllers. In the literature, this type of advanced controllers has been used and compared with classic PID controllers[13], showing a good behaviour. Based on previous works[1][9], our research group has been working with DMC controllers obtaining some accurate and efficient neuronal implementations[5], even for Linked Multi-Component Robotic Systems (LMCRS)[6][7]. Along the development of these works, we have realized the importance of certain parameters on the performance of predictive controllers. Ttherefore, apart from the previous works our group has also conducted a systematic study to analyze the effect of the lambda parameter on the DMC controllers performance[4]. However, we have neither studied nor found in the literature any study about the influence of the prediction horizon p of the DMC controller, because it is usually supposed a fixed implementation of the predictive controller, which is defined by a concrete p value. The main objective of this paper is to study the effect of the p parameter in the performance of a DMC controller.The paper is structured as follows. In the second section, we recall some basic concepts of MPC and DMC to address the importance and the role of the p parameter in such control scheme. In the third section, we describe the experimental design we have carried out, detailing the indexes we have used to describe the performance of the DMC controllers, the system and the working point they have been working in to assess the effect of changes in the p parameter and the tested values for that parameter. In the fourth section, we discuss the experimental results that we have obtained, enumerating the particular effect caused in each of the performance indexes. The last section provides our conclusions. Finally, we have added four appendixes with figures which summarize the 720 experiments that have been carried out along this study.
2. Background
This section reviews some basic concepts about Model Predictive Control (MPC) as a general technique, and about a concrete technique called Dynamic Matrix Control (DMC).
2.1. Model Predictive Control (MPC)
MPC is an advanced control technique used to deal with systems that are not controllable using classic control schemas. This kind of controllers works like the human brain in the sense that instead of using the past error between the output of the system and the desired value, it controls the system predicting the value of the output in a short time, so the system output is as closer as possible to its desired value for these moments. Predictive Control is not a concrete technique, it is a set of techniques that have several common characteristics: there is a world model which is used to predict the system output from the actual moment until p samples, an objective function that must be minimized and a control law which minimizes the objective function. A predictive controller follows the following steps:→ Each sampling time, through the system model, the controller calculates the system output from now until p sampling times (prediction horizon), which depends on the future control signals that the controller will generate.→A set of m control signals is calculated optimizing the objective function to be used along m sampling times (control horizon).→In each sampling time only the first of the set of m control signals is used, and at the next sampling time, all the process is repeated again.The concept of Predictive Control is a set of techniques that share certain characteristics, and the engineer has liberty to choose them. So, there are several types of predictive controllers. These common characteristics are the following: →There is a plant model, and it can be used a step response model, an impulse step response model, a transfer function, etc.→There is an objective function that the controller has to optimize.→There is a control law to minimize the objective function. To learn more about Predictive Control in general and about diverse predictive control algorithms, see[3],[2],[8], [12],[10] and[11].
2.2. Dynamic Matrix Control (DMC)
DMC is a concrete MPC algorithm that fixes each of the three characteristics we have described previously as we will see below. To learn more about Dynamic Matrix Control, see[3],[2],[8] and[12].
2.2.1. System Model
The plant model used by DMC algorithm is the step response model. This model uses the 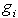 coefficients that are the output of the lineal system when it is excited using a step. To reduce the number of coefficients we assume that the system is stable and the output does not change after some sampling time k. The expression of the output of the system is given through eq. (1):
coefficients that are the output of the lineal system when it is excited using a step. To reduce the number of coefficients we assume that the system is stable and the output does not change after some sampling time k. The expression of the output of the system is given through eq. (1):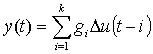 | (1) |
2.2.2. Prediction Model
Using the step response model to model the system and maintaining the hypothesis that perturbations over the system are constants, it is possible to calculate a prediction at the instant t of the output until the instant 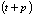 under the effect of m control actions. That prediction is given by the eq. (2):
under the effect of m control actions. That prediction is given by the eq. (2):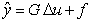 | (2) |
being 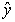 the prediction of the output,
the prediction of the output, 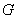 a matrix which contains the system dynamics and
a matrix which contains the system dynamics and 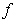 the free response of the system. In eq. (3) we show the dimensions of the matrix and vectors involved in eq. (2).
the free response of the system. In eq. (3) we show the dimensions of the matrix and vectors involved in eq. (2). | (3) |
In eq. (4) we describe how the free response of the system 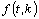 is calculated:
is calculated: 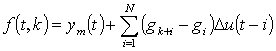 | (4) |
Control Law The derivation of the control law is based on the existence of an objective function, which uses the future outputs prediction model that we have described before. As objective function we used the described by eq. (5).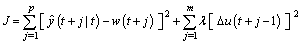 | (5) |
We have to minimize the difference between the reference and the output prediction along a prediction horizon p with the m control actions generated in the control horizon, modulating the roughness in the variation of the manipulated variables using the λ parameter. Minimizing the objective function 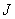 described in eq. (5) we obtain the following expression, which produces m control actions, although at t only one of them is used:
described in eq. (5) we obtain the following expression, which produces m control actions, although at t only one of them is used: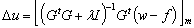 | (6) |
After this brief introduction, we can understand the role of the p parameter and intuit which might be the influence on the controller performance due to changes in that parameter.
3. Experimental Design
In this section we provide the experimental design of the study we have carried out to assess the influence of the prediction horizon parameter in DMC controllers performance. First, we detail the definition of the performance indexes that we have used. Then, the system whose response will be analysed is specified in a motivated way. We also discuss the working point of the controlled system. Finally, we specify the set of experiments that we have carried out to obtain significant results.
3.1. Performance Indexes Definition
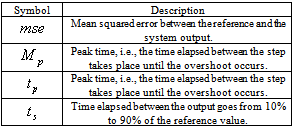
 | Figure 1. Graphical representation of the performance indexes |
Table 1. Symbol and description of several performance indexes used in the experimental design
 |
| |
|
To assess the influence of the p parameter of the DMC controller we have defined several indexes. These indexes are focused on the performance reached at the output of the system when it is controlled by a MPC controller and when the reference is a unitary step of arbitrary frequency. The indexes we have used to measure the performance are described in Table 1. Besides, Figure 1 shows a graphical representation of those indexes.
3.2. System and Working Point to Study
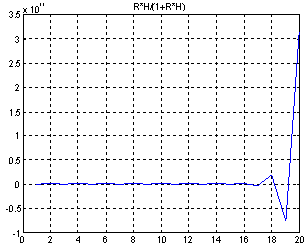
We have analysed the discretized system described by eq. (7). This is a quite simple but interesting system because it shows an unstable response when the reference is a unitary step and it is controlled by a discretized Proportional-Integral-Derivative (PID) controller in a closed loop configuration, which has been tuned by means of the Ziegler-Nichols method. That unstable response is shown in Figure 2.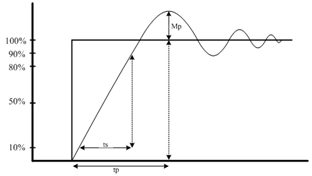 | Figure 2. Unstable response of the system when it is controlled by a discretized PID controller |
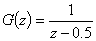 | (7) |
To determine the working point of the system, i.e., the frequency of the unitary step signal which is at the input of the closed loop system as reference, we have used the Bode diagram shown in Figure 3. Based on that diagram, we have chosen a frequency of 30 sample times because it is a frequency at which the given gain is representative of many other frequencies for that system.
3.3. Sensitivity Analysis
As stated before, the main objective of this paper is to analyse the influence of the prediction horizon parameter in DMC controllers. Therefore, we have studied the behaviour of the previously specified system at that working point when it is controlled by DMC controllers varying the value of the p parameter. The values which have been chosen are 1, 3, 6, 10, 15 and 20. The values of the λ parameter are 10-3, 10-2, 10-1, 1, 101 and 102.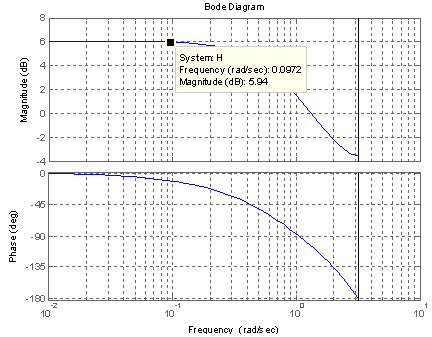 | Figure 3. Bode diagram used to determine the working point of the system |
4. Experimental Results
In this section we provide several results regarding to the performance indexes which we introduced in the section devoted to the experimental design, i.e., the parameter sensitivity analysis specified in that section is carried out.
4.1. Effect on Mse Value
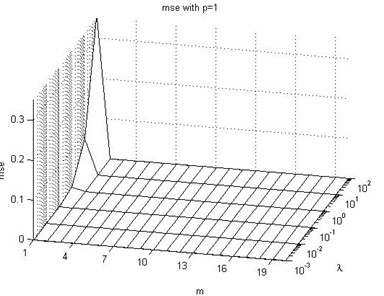
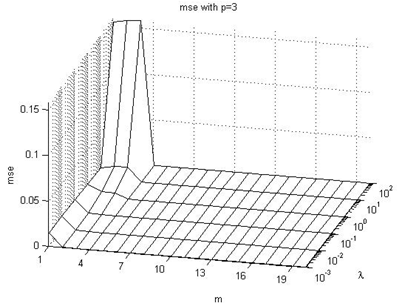
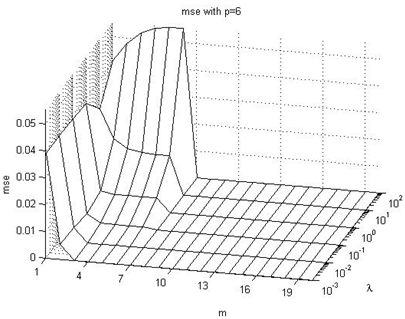
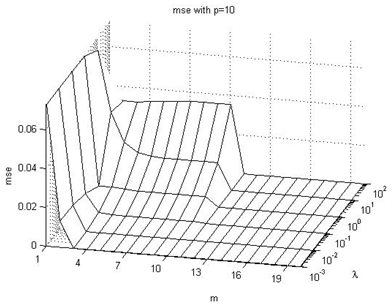
In this subsection we are going to enumerate the effects on the  performance index values, taking into consideration Figures 4-9 of the Appendix I. The following are the main conclusions:→In general, we can see that with increasing values of the p parameter, the value of the
performance index values, taking into consideration Figures 4-9 of the Appendix I. The following are the main conclusions:→In general, we can see that with increasing values of the p parameter, the value of the  index becomes lower for each combination of
index becomes lower for each combination of  parameters values.→The
parameters values.→The 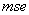 index value ranges from about 10-7 to about 3.10-1, with different combinations of
index value ranges from about 10-7 to about 3.10-1, with different combinations of 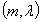 parameters values.→The worst results are produced when the λ parameter is very high, but if the control horizon parameter m increases, the results are relatively better.→As the p parameter value increases, the
parameters values.→The worst results are produced when the λ parameter is very high, but if the control horizon parameter m increases, the results are relatively better.→As the p parameter value increases, the 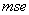 index value becomes relatively low, however it increases again when p≥10.→The most likely reason for this effect is that it is convenient to predict the output of the system, but if we try to predict it at a very distant sample time, that prediction will be less accurate.→Also, we can notice that it makes no sense to use a control horizon m larger than the prediction horizon p.
index value becomes relatively low, however it increases again when p≥10.→The most likely reason for this effect is that it is convenient to predict the output of the system, but if we try to predict it at a very distant sample time, that prediction will be less accurate.→Also, we can notice that it makes no sense to use a control horizon m larger than the prediction horizon p.
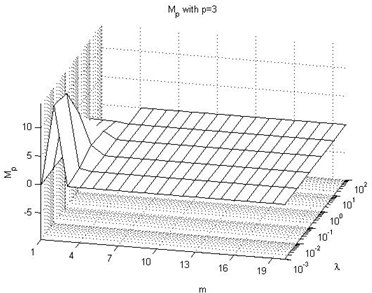
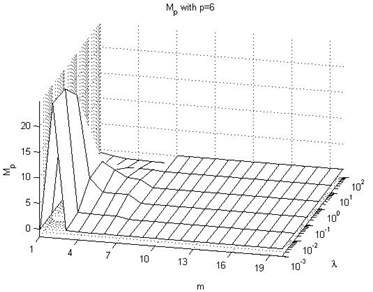
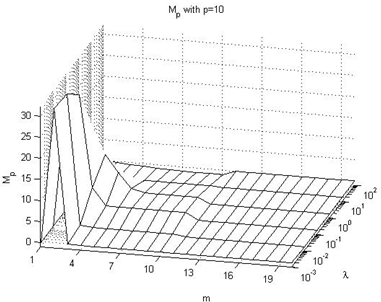
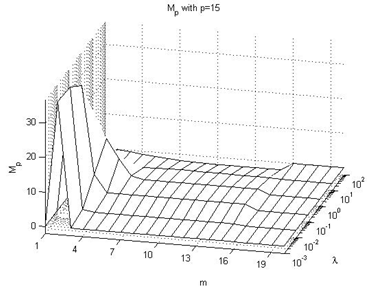
4.2. Effect on Mp value
In this subsection we summarize the effect on the Mp performance index values, taking into consideration Figures 10-15 of the Appendix II, being these the main conclusions:→In all cases, independently of the value of the prediction horizon, the overshot is less that 0 when there is a high value of the lambda parameter because the reference value is not reached. This circumstance is clearly observed when p=1 and p=3.→Independently of the value of the prediction horizon p, if the control horizon m is small, the Mp value increases reaching peak values larger to 30% when the value of the λ parameter is small and p≥10.→In the remaining situations, the effect of the p parameter is not significant because the Mp values are near to 5%.
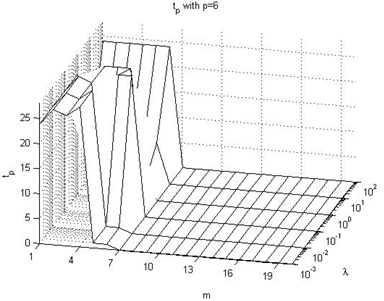
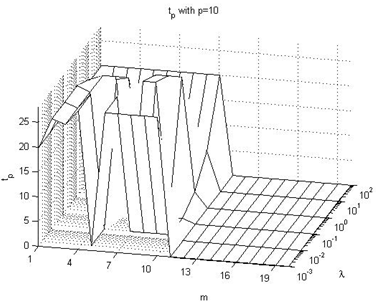
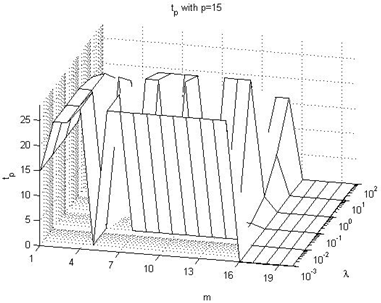
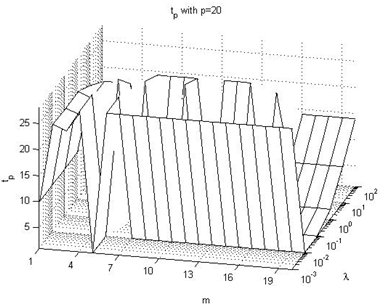
4.3. Effect on tp value
In this subsection we summarize the effect on the tp performance index values, taking into consideration Figures 16-21 of the Appendix III, being these the main conclusions:→There is not a clear influence of the prediction horizon parameter on the moment when the overshoot takes place (the tp performance index), because its value does not experiment large changes due to the p parameter value, but rather due to the λ parameter. Its value is usually around 20 or 30 sample times, and the peak usually occurs at the end of the pulse, just before the falling edge.→The main conclusion is that it takes place on the range of 20-30 seconds after the unitary step signal with the most of the configurations. Only when p=1, in some configurations it takes place before of 5 seconds after the reference signal.
4.4. Effect on ts value
In this subsection we expose the effect on the ts performance index values, taking in consideration Figures 22-27 of the Appendix IV. The following are the main conclusions:→It looks like the prediction horizon parameter does not have a great influence on this performance index. Its value depends more on lambda than on p or m. →The values go from 0 with very small values of the λ parameter to 25 with very large values of λ, occurring peaks with intermediate values (not extreme) of p parameter.
5. Conclusions
In this paper we have studied the influence of the p parameter on DMC controllers performance. We have introduced the MPC and DMC controllers to frame the importance of the prediction horizon. In the experimental design we have specified the performance indexes which we have taken into account and the values used to the p parameter. Once we have carried out a number of experiments, we have discussed the main results regarding to each of the indexes. We have tested 120 structures of DMC controllers for each value of prediction horizon, and as summary, with the specificities that we have shown through figures, we can conclude that a low-intermediate value of the p parameter results in a better performance of the DMC controllers.
ACKNOWLEDGEMENTS
The research was supported by Grant 6397 of Teaching Innovation Projects 2011-13 of the Education Advisory Service, Vicerectorship for Teaching Quality and Innovation, Basque Country University (UPV/EHU), whose support is greatly acknowledged.The authors would like to thank the cooperative work developed by the students who kindly participated in the previously referred project using cooperative learning techniques, which was supervised by the authors.
APENDIX I. Influence on 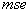 value
value
 | Figure 4. mse with p=1 |
 | Figure 5. mse with p=3 |
 | Figure 6. mse with p=6 |
 | Figure 7. mse with p=10 |
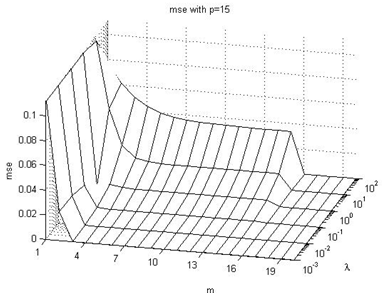 | Figure 8. mse with p=15 |
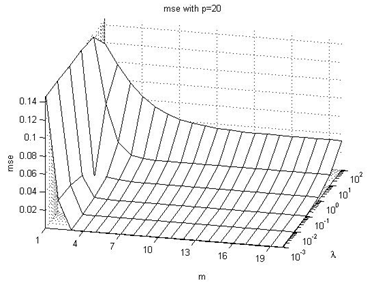 | Figure 9. mse with p=20 |
APENDIX II. Influence on 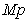 value
value
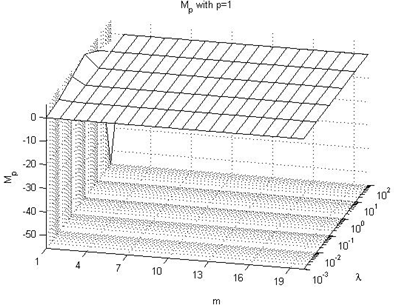 | Figure 10. Mp with p=1 |
 | Figure 11. Mp with p=3 |
 | Figure 12. Mp with p=6 |
 | Figure 13. Mp with p=10 |
 | Figure 14. Mp with p=15 |
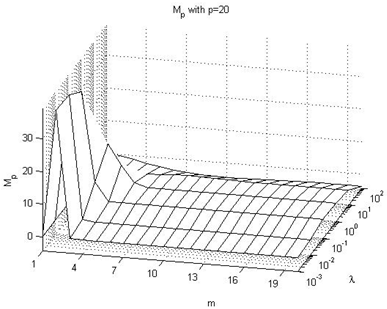 | Figure 15. Mp with p=20 |
APENDIX III. Influence on  value
value
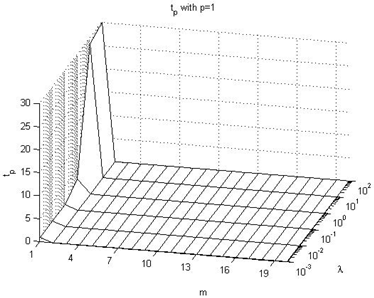 | Figure 16. tp with p=1 |
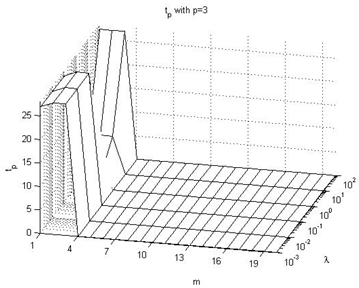 | Figure 17. tp with p=3 |
 | Figure 18. tp with p=6 |
 | Figure 19. tp with p=10 |
 | Figure 20. tp with p=15 |
 | Figure 21. tp with p=20 |
APENDIX IV. Influence on 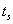 value
value
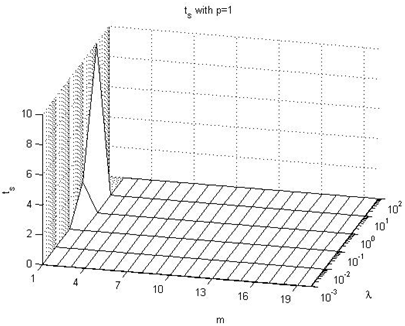 | Figure 22. ts with p=1 |
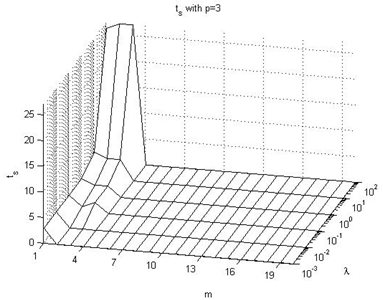 | Figure 23. ts with p=3 |
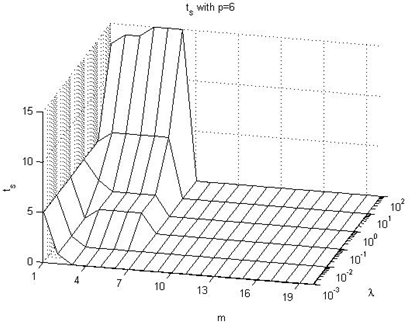 | Figure 24. ts with p=6 |
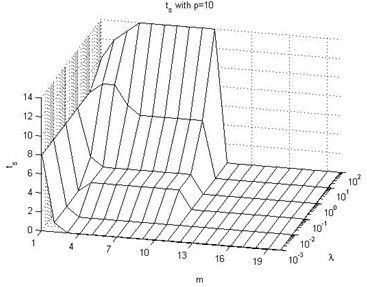 | Figure 25. ts with p=10 |
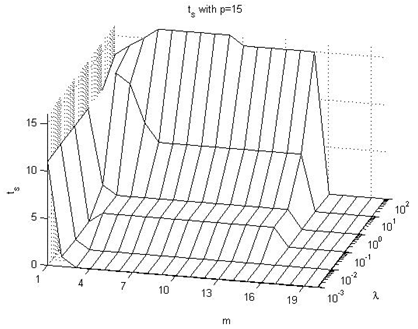 | Figure 26. ts with p=15 |
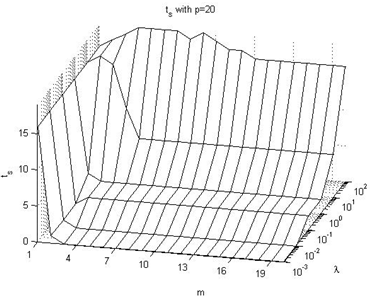 | Figure 27. ts with p=20 |
References
| [1] | M.R. Arahal, M. Berenguel, E.F. Camacho, “Neural identification applied to predictive control of a solar plant”, Elsevier, Control Engineering Practice, vol. 6, pp. 333-344, 1998 |
| [2] | E.F. Camacho, C. Bordons, Model Predictive Control, Springer-Verlag, United Kingdom, 2004. |
| [3] | E.F. Camacho, C. Bordons, Model Predictive Control in the Process Industry, Springer-Verlag, United Kingdom, 1995. |
| [4] | J.M. Lopez-Guede, B. Fernadez-Gauna, M. Graña, F. Oterino, J.M. Larrañaga, "Effect of the Lambda Parameter in Dynamic Matrix Controllers Performance", Publishing Services LLC, Journal of Computer and Information Technology, vol. 2, no. 2, pp. 81-88, 2012. |
| [5] | J.M. López-Guede, M. Graña, E. Zulueta, O. Barambones, “Economical Implementation of Control Loops for Multi-robot Systems” in Proceedings of 15th International Conference on Neural Information Processing, ICONIP 2008, pp. 1053-1059, 2008. |
| [6] | J.M. Lopez-Guede, E. Zulueta, B. Fernández and M. Graña, "Multi-Robot Systems Control Implementation" in Robot Learning, ed. Dr. Suraiya Jabin, Sciyo, pp. 137-150, 2010. |
| [7] | J.M. López-Guede, E. Zulueta, M. Graña, A. D’Anjou, “Neuronal Implementation of Predictive Controllers”. Proceedings of 5th International Conference on Hybrid Artificial Intelligence Systems, HAIS 2010, pp. 312-319, 2010. |
| [8] | J. M. Maciejowski, Predictive Control with Constraints, Prentice Hall, United Kingdom, 2002. |
| [9] | J.L. McKinstry, G.M. Edelman, J.L. Krichmar, “A cerebellar model for predictive motor control tested in a brain-based device”. Proceedings of the National Academy of Sciences of The United States of America, vol. 103, no. 9, pp. 3387-3392, 2006. |
| [10] | J.B. Rawlings, “Tutorial: Model Predictive Control Technology”, Proceedings of the American Control Conference, pp. 662-676, 1999. |
| [11] | R. Soeterboek, Predictive control, A unified approach, Prentice Hall, USA, 1992. |
| [12] | H. Sunan, T. Kok, L. Tong, Applied Predictive Control, Springer-Verlag, United Kingdom, 2002. |
| [13] | M. Voicu, C. Lazär, F. Schönberger, O. Pästravanu, S. Ifrim, Control Engineering Solution: a Practical Approach, Predictive Control vs. PID Control of Thermal Treatment Processes, Control Engineering Solution: a Practical Approach. pp. 163-174, The Institution of Electrical Engineers, United Kingdom, 1997 |

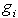 coefficients that are the output of the lineal system when it is excited using a step. To reduce the number of coefficients we assume that the system is stable and the output does not change after some sampling time k. The expression of the output of the system is given through eq. (1):
coefficients that are the output of the lineal system when it is excited using a step. To reduce the number of coefficients we assume that the system is stable and the output does not change after some sampling time k. The expression of the output of the system is given through eq. (1):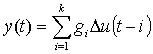
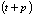 under the effect of m control actions. That prediction is given by the eq. (2):
under the effect of m control actions. That prediction is given by the eq. (2):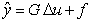
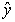 the prediction of the output,
the prediction of the output, 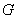 a matrix which contains the system dynamics and
a matrix which contains the system dynamics and 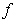 the free response of the system. In eq. (3) we show the dimensions of the matrix and vectors involved in eq. (2).
the free response of the system. In eq. (3) we show the dimensions of the matrix and vectors involved in eq. (2).
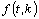 is calculated:
is calculated: 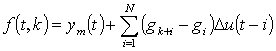
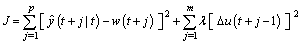
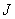 described in eq. (5) we obtain the following expression, which produces m control actions, although at t only one of them is used:
described in eq. (5) we obtain the following expression, which produces m control actions, although at t only one of them is used: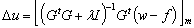


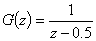

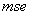 performance index values, taking into consideration Figures 4-9 of the Appendix I. The following are the main conclusions:→In general, we can see that with increasing values of the p parameter, the value of the
performance index values, taking into consideration Figures 4-9 of the Appendix I. The following are the main conclusions:→In general, we can see that with increasing values of the p parameter, the value of the 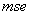 index becomes lower for each combination of
index becomes lower for each combination of 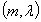 parameters values.→The
parameters values.→The 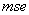 index value ranges from about 10-7 to about 3.10-1, with different combinations of
index value ranges from about 10-7 to about 3.10-1, with different combinations of 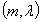 parameters values.→The worst results are produced when the λ parameter is very high, but if the control horizon parameter m increases, the results are relatively better.→As the p parameter value increases, the
parameters values.→The worst results are produced when the λ parameter is very high, but if the control horizon parameter m increases, the results are relatively better.→As the p parameter value increases, the 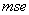 index value becomes relatively low, however it increases again when p≥10.→The most likely reason for this effect is that it is convenient to predict the output of the system, but if we try to predict it at a very distant sample time, that prediction will be less accurate.→Also, we can notice that it makes no sense to use a control horizon m larger than the prediction horizon p.
index value becomes relatively low, however it increases again when p≥10.→The most likely reason for this effect is that it is convenient to predict the output of the system, but if we try to predict it at a very distant sample time, that prediction will be less accurate.→Also, we can notice that it makes no sense to use a control horizon m larger than the prediction horizon p.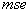 value
value





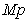 value
value





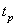 value
value





 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML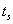 value
value





