-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2012; 2(6): 172-180
doi: 10.5923/j.control.20120206.05
Robust Adaptive Fuzzy Control of MIMO Nonlinear Systems with Higher-Order and Unmatched Uncertainties
Chiang-Cheng Chiang
Department of Electrical Engineering, Tatung University, 40 Chung-Shan North Road, Sec.3, Taipei, Taiwan, Republic of China
Correspondence to: Chiang-Cheng Chiang, Department of Electrical Engineering, Tatung University, 40 Chung-Shan North Road, Sec.3, Taipei, Taiwan, Republic of China.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, a robust adaptive fuzzy controller is designed for the output tracking control problem of multi-input multi-output (MIMO) nonlinear systems with higher-order and unmatched uncertainties. For real mechanical systems, the strength of the unmatched uncertainties is bounded by the pth-order polynomials in states, in contrast to other works assuming that these uncertainties are bounded by the first-order polynomials in states. Based on the combination of the 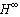 optimal control with fuzzy systems and some feasible adaptation laws, the proposed robust adaptive fuzzy controller can not only guarantee that all the signals in the whole closed-loop systems are bounded, but also obtain that the output tracking performance of MIMO nonlinear uncertain systems is well established. A series of computer simulations are illustrated to demonstrate the validity of the proposed control scheme.
optimal control with fuzzy systems and some feasible adaptation laws, the proposed robust adaptive fuzzy controller can not only guarantee that all the signals in the whole closed-loop systems are bounded, but also obtain that the output tracking performance of MIMO nonlinear uncertain systems is well established. A series of computer simulations are illustrated to demonstrate the validity of the proposed control scheme.
Keywords:
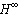 Optimal Control, Fuzzy Systems, Output Tracking, Unmatched Uncertainties, Adaptation Law
Optimal Control, Fuzzy Systems, Output Tracking, Unmatched Uncertainties, Adaptation Law
Cite this paper: Chiang-Cheng Chiang, "Robust Adaptive Fuzzy Control of MIMO Nonlinear Systems with Higher-Order and Unmatched Uncertainties", International Journal of Control Science and Engineering, Vol. 2 No. 6, 2012, pp. 172-180. doi: 10.5923/j.control.20120206.05.
Article Outline
1. Introduction
- The adaptive control of nonlinear systems has attracted a lot of attention, and significant progress has been made in recent years and novel techniques facilitated by advances in geometric nonlinear control theory and in particular input-output feedback linearization method[1,2]. The central concept of this approach is to transform the nonlinear system dynamics into an equivalent linear system, so that the conventional linear control techniques can be applied.The approach requires a perfect model of the plant in order to achieve linearization of the closed-loop system. However, there often exist inevitable uncertainties in the constructed models of many real systems. In addition, some uncertain parameters are not exactly known or difficult to estimate. Generally speaking, uncertainties in the feedback linearization include the matched uncertainties[3,4] and the unmatched (mismatched) uncertainties[5,6]. For many practical systems, unmatched uncertainties are common in control practice. Therefore, the design of a robust adaptive controller that deals with unmatched uncertainties of a nonlinear system is an important subject.So far, the systematic design of input-output linearizable systems with the unmatched uncertainties has been conducted, and three main extension systems have been proposed: (1) adaptive control[7]; (2) Lyapunov-based control[8]; (3) variable structure control[9,10], to increase the robustness and to improve the performance of the controlled nonlinear system. Recently
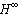 optimal control theory has been well developed and found extensive application to efficiently treat the robust stabilization and disturbance rejection problems[11-13]. In this paper, we combine
optimal control theory has been well developed and found extensive application to efficiently treat the robust stabilization and disturbance rejection problems[11-13]. In this paper, we combine 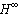 control technique with adaptive control to deal with unmatched uncertainties.In the past few years, there has been rapidly growing interest in fuzzy control of nonlinear systems, and there have been many successful applications. The most important issue for fuzzy control systems is how to get a system design with the guarantee of stability and control performance. Meanwhile, recently there have been significant research efforts on the issue of stability in fuzzy control systems[15-18]. In[19, 20], based on feedback linearization technique, adaptive fuzzy control schemes have been introduced to deal with nonlinear systems. However, their results were valid while the controlled nonlinear systems did not include the unmatched uncertainties.In this paper, the main objective is to design a robust adaptive fuzzy controller for a class of unknown MIMO nonlinear systems with higher-order and unmatched uncertainties. Also, the strength of the unmatched uncertainties is bounded by the pth-order polynomials in states, unlike other works[14,21,22] based on the assumption that these uncertainties are bounded by the first-order polynomials in states. First, the theory of state feedback input output linearization is applied to the MIMO nonlinear systems with unmatched uncertainties. The resulting normal systems with unmatched uncertainties will be in a minimum phase system. Next, the fuzzy systems and some adaptive laws are applied to approximate the unknown nonlinear functions and estimate the upper bounds of the unknown uncertainties, respectively. However, these unmatched uncertainties including modeling errors (fuzzy system approximation errors) and parameter variations, etc., can lead to the instability of the closed-loop system; therefore, a robust compensator is designed by
control technique with adaptive control to deal with unmatched uncertainties.In the past few years, there has been rapidly growing interest in fuzzy control of nonlinear systems, and there have been many successful applications. The most important issue for fuzzy control systems is how to get a system design with the guarantee of stability and control performance. Meanwhile, recently there have been significant research efforts on the issue of stability in fuzzy control systems[15-18]. In[19, 20], based on feedback linearization technique, adaptive fuzzy control schemes have been introduced to deal with nonlinear systems. However, their results were valid while the controlled nonlinear systems did not include the unmatched uncertainties.In this paper, the main objective is to design a robust adaptive fuzzy controller for a class of unknown MIMO nonlinear systems with higher-order and unmatched uncertainties. Also, the strength of the unmatched uncertainties is bounded by the pth-order polynomials in states, unlike other works[14,21,22] based on the assumption that these uncertainties are bounded by the first-order polynomials in states. First, the theory of state feedback input output linearization is applied to the MIMO nonlinear systems with unmatched uncertainties. The resulting normal systems with unmatched uncertainties will be in a minimum phase system. Next, the fuzzy systems and some adaptive laws are applied to approximate the unknown nonlinear functions and estimate the upper bounds of the unknown uncertainties, respectively. However, these unmatched uncertainties including modeling errors (fuzzy system approximation errors) and parameter variations, etc., can lead to the instability of the closed-loop system; therefore, a robust compensator is designed by 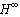 control technique to reject this kind of uncertainties. The proposed control scheme not only guarantees the uniform ultimate boundedness, but also makes the maximum tracking error less than or equal to a desired attenuation level due to the unmatched uncertainties.This paper is organized as follows. First, Section 2 describes the problem of robust output tracking for MIMO nonlinear system with higher-order and unmatched uncertainties. Then, necessary preliminaries on feedback linearization are presented, and some necessary assumptions are introduced. In Section 3, a brief description of fuzzy systems is made. In Section 4, a robust adaptive fuzzy controller is proposed such that the output of the controlled system with higher-order and unmatched uncertainties exponentially tracks the given desired trajectory. In Section 5, the simulations and discussions are presented to confirm the validity of the proposed control scheme. Finally, a conclusion is given in Section 6.
control technique to reject this kind of uncertainties. The proposed control scheme not only guarantees the uniform ultimate boundedness, but also makes the maximum tracking error less than or equal to a desired attenuation level due to the unmatched uncertainties.This paper is organized as follows. First, Section 2 describes the problem of robust output tracking for MIMO nonlinear system with higher-order and unmatched uncertainties. Then, necessary preliminaries on feedback linearization are presented, and some necessary assumptions are introduced. In Section 3, a brief description of fuzzy systems is made. In Section 4, a robust adaptive fuzzy controller is proposed such that the output of the controlled system with higher-order and unmatched uncertainties exponentially tracks the given desired trajectory. In Section 5, the simulations and discussions are presented to confirm the validity of the proposed control scheme. Finally, a conclusion is given in Section 6.2. Problem Formulation
- Consider a class of MIMO nonlinear systems in the presence of the unmatched uncertainties of the following form:
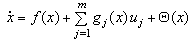 | (1) |
 where
where 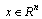 is the measured state vector,
is the measured state vector, 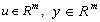 are the system input vector and output vector, respectively.
are the system input vector and output vector, respectively. 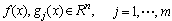 are sufficiently smooth vector fields,
are sufficiently smooth vector fields, 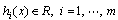 are sufficiently smooth output functions, and
are sufficiently smooth output functions, and 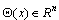 represent uncertainties continuously differentiable with respect to x.First, we pursue the input-output linearization process for a MIMO dynamics. In the following definitions, the notation
represent uncertainties continuously differentiable with respect to x.First, we pursue the input-output linearization process for a MIMO dynamics. In the following definitions, the notation 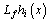 and
and 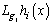 denote, the Lie derivatives of the function
denote, the Lie derivatives of the function 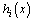 with respect to the vector field
with respect to the vector field 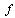 and
and 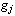 , receptively. Higher-order Lie derivative can be defined recursively such as
, receptively. Higher-order Lie derivative can be defined recursively such as 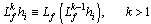 .Definition 1[1]: A multivariable nonlinear system of the form (1) is said to have a (vector) relative degree
.Definition 1[1]: A multivariable nonlinear system of the form (1) is said to have a (vector) relative degree 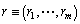 at a point
at a point 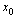 if (ⅰ)
if (ⅰ) 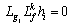 for all
for all 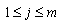 , for all
, for all 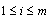 , for all
, for all 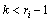 , and for all
, and for all 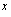 in a neighborhood of
in a neighborhood of 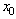 .(ⅱ) The
.(ⅱ) The 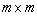 matrix
matrix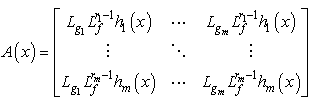 | (2) |
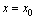 Throughout this paper, we assume that the system (1) possesses a relative degree in its domain of definition. Based on this assumption we have the following proposition.Proposition 1[1]: Suppose a system has a (vector) relative degree
Throughout this paper, we assume that the system (1) possesses a relative degree in its domain of definition. Based on this assumption we have the following proposition.Proposition 1[1]: Suppose a system has a (vector) relative degree 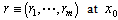 , then
, then 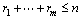 . Let
. Let 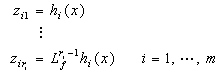 | (3) |
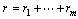 is strictly less than n, it is always to find
is strictly less than n, it is always to find 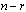 smooth functions
smooth functions 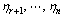 such that the mapping
such that the mapping 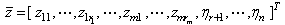 | (4) |
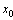 . The
. The 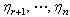 are chosen to satisfy
are chosen to satisfy 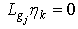 | (5) |
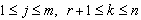 , and all
, and all 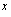 around
around 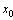 .Now, we set
.Now, we set 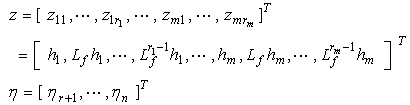 | (6) |
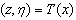 which transforms the system (1) into the following normal form:
which transforms the system (1) into the following normal form: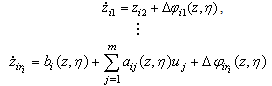
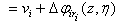 | (7) |
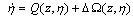 | (8) |
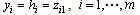 | (9) |
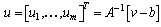 | (10) |
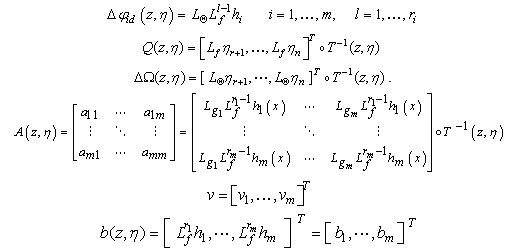 Assumption 1: The zero dynamics (8) is exponentially stable in the domain of definition, and the function
Assumption 1: The zero dynamics (8) is exponentially stable in the domain of definition, and the function 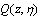 is Lipschitz in
is Lipschitz in  and uniformly in
and uniformly in 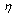 . Moreover, the norm of the uncertainty vector
. Moreover, the norm of the uncertainty vector 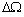 satisfies the following condition:
satisfies the following condition: 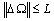 .Assumption 2: Let
.Assumption 2: Let 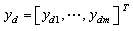 be the desired output trajectories. The desired trajectories
be the desired output trajectories. The desired trajectories 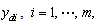 and their first
and their first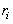 derivatives are uniformly bounded, that is
derivatives are uniformly bounded, that is 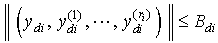 for a bounded positive constant
for a bounded positive constant 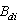 .Define the output tracking errors to be
.Define the output tracking errors to be 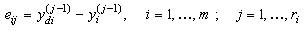 | (11) |
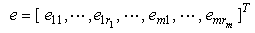 | (12) |
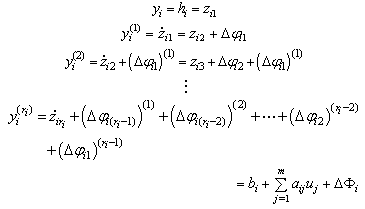 | (13) |
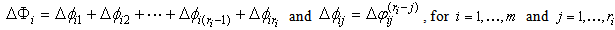 .Assumption 3: If the
.Assumption 3: If the 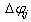 is the function that has continuous derivatives in the domain of definition. These derivatives are bounded by the polynomial which is combined with both
is the function that has continuous derivatives in the domain of definition. These derivatives are bounded by the polynomial which is combined with both 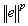 and
and 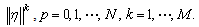 That is,
That is,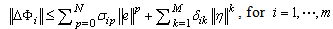 | (14) |
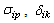 are unknown positive constants.In accordance with (14), we will choose the simple adaptive laws to estimate the upper bounds of these higher-order uncertainties. The simple adaptive laws can be represented as follows:
are unknown positive constants.In accordance with (14), we will choose the simple adaptive laws to estimate the upper bounds of these higher-order uncertainties. The simple adaptive laws can be represented as follows: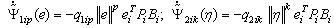 | (15) |
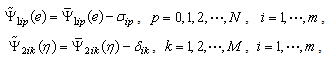 are the parameter adaptation errors and
are the parameter adaptation errors and 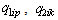 are the adaptation gains with the positive values. Because
are the adaptation gains with the positive values. Because 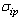 and
and 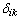 are unknown positive constants, the adaptive laws can be written as
are unknown positive constants, the adaptive laws can be written as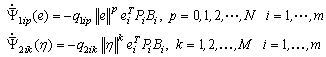 | (16) |
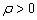 such that the following
such that the following 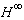 tracking performance index is achieved.
tracking performance index is achieved.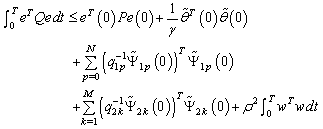 | (17) |
 is the combined fuzzy approximation errors,
is the combined fuzzy approximation errors,  are positive matrix of proper dimension,
are positive matrix of proper dimension, 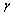 is a designed parameter. If the system stars with initial conditions
is a designed parameter. If the system stars with initial conditions 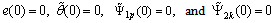 then performance in (17) can be rewritten as
then performance in (17) can be rewritten as 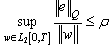 | (18) |
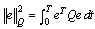 and
and 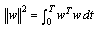 , i.e., the
, i.e., the 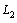 gain from
gain from 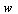 to the tracking error
to the tracking error 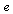 must be equal to or less than
must be equal to or less than 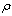 .
.3. Robust Adaptive Controller Design Using Fuzzy Systems
- The fuzzy systems are universal approximations from the viewpoint of human experts and can uniformly approximate nonlinear continuous functions to arbitrary accuracy[14]. The basic configuration of the fuzzy system consists of four main components: fuzzy rule base, fuzzy inference engine, fuzzifier and defuzzifier . The fuzzy system performs a mapping from
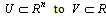 . Let
. Let 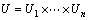 where
where 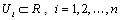 . Wang[16] presents a detailed description of each of the four blocks in the fuzzy system. The fuzzy rule base consists of a collection of fuzzy IF-THEN rules:
. Wang[16] presents a detailed description of each of the four blocks in the fuzzy system. The fuzzy rule base consists of a collection of fuzzy IF-THEN rules: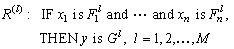 where
where 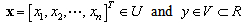 are the input and output of the fuzzy system,
are the input and output of the fuzzy system, 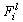 and
and 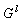 are fuzzy sets in
are fuzzy sets in 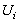 and
and 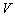 , respectively.
, respectively. 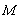 is the number of rules. The fuzzifier maps a crisp point
is the number of rules. The fuzzifier maps a crisp point 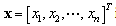 into a fuzzy set in
into a fuzzy set in 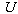 . The fuzzy inference engine performs a mapping from fuzzy sets in
. The fuzzy inference engine performs a mapping from fuzzy sets in 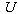 to fuzzy sets in
to fuzzy sets in 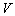 , based upon the fuzzy IF-THEN rules in the fuzzy rule base and the compositional rule of inference. The defuzzifier maps a fuzzy set in
, based upon the fuzzy IF-THEN rules in the fuzzy rule base and the compositional rule of inference. The defuzzifier maps a fuzzy set in 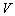 to a crisp point in
to a crisp point in 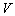 . The fuzzy systems with center-average defuzzifier, product inference, and singleton fuzzifier are of the following form:
. The fuzzy systems with center-average defuzzifier, product inference, and singleton fuzzifier are of the following form: 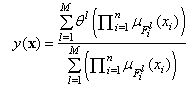 | (19) |
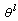 is the point at which fuzzy membership function
is the point at which fuzzy membership function 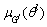 of fuzzy sets
of fuzzy sets 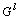 achieves its maximum value, and it is assumed that
achieves its maximum value, and it is assumed that 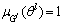 . Eq. (19) can be rewritten as
. Eq. (19) can be rewritten as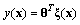 | (20) |
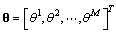 is a parameter vector,
is a parameter vector, 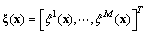 is a regressive vector with the regressor
is a regressive vector with the regressor 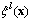 , which is defined as fuzzy basis function
, which is defined as fuzzy basis function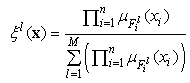 | (21) |
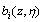 and
and 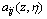 will be approximated by tuning the parameters of the corresponding fuzzy systems. In this situation,
will be approximated by tuning the parameters of the corresponding fuzzy systems. In this situation, 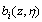 and
and 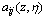 in (7) will be approximated by the following fuzzy systems
in (7) will be approximated by the following fuzzy systems 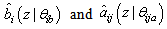 respectively.
respectively.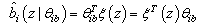 | (22) |
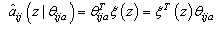 | (23) |
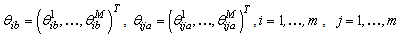 .Due to the existence of fuzzy approximation errors and unmatched uncertainties, the resulting robust adaptive fuzzy controller can be chosen as
.Due to the existence of fuzzy approximation errors and unmatched uncertainties, the resulting robust adaptive fuzzy controller can be chosen as 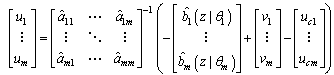 | (24) |
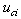 is the robust compensator defined as
is the robust compensator defined as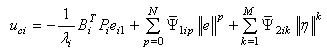 | (25) |
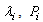 are the solutions of the following Riccati equation[19]
are the solutions of the following Riccati equation[19]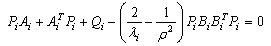 | (26) |
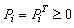 if and only if
if and only if 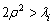 . Moreover, the auxiliary control input can be chosen as
. Moreover, the auxiliary control input can be chosen as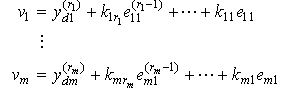 | (27) |
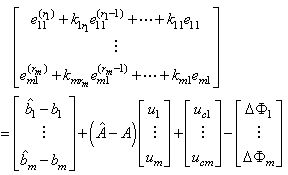 | (28) |
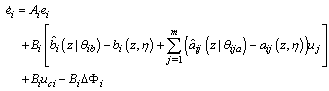 | (29) |
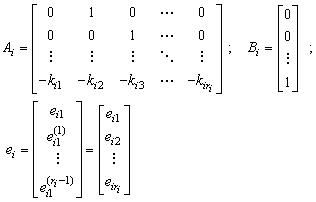 Moreover, the coefficients
Moreover, the coefficients 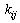 are chosen such that the matrices
are chosen such that the matrices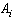 are Hurwitz for
are Hurwitz for 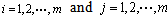 Now let the optimal parameter estimates
Now let the optimal parameter estimates 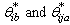 be defined as follows[16]:
be defined as follows[16]: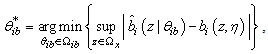
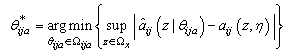 | (30) |
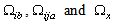 denote the sets of suitable bounds on
denote the sets of suitable bounds on 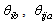 , and z , respectively. The minimum approximation errors[15,16] is defined as
, and z , respectively. The minimum approximation errors[15,16] is defined as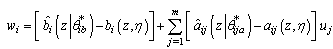 | (31) |
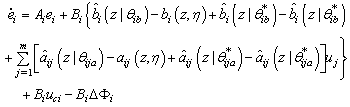
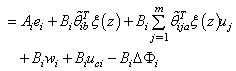 | (32) |
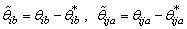 The parameter adaptive laws are chosen as
The parameter adaptive laws are chosen as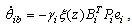 | (33) |
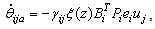 | (34) |
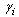 and
and 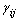 are positive constants.Theorem 1: Consider the MIMO nonlinear uncertain system (1) and Assumptions 1-3 are satisfied. If the robust adaptive fuzzy control scheme in (24)-(27) with the learning adaptive laws in (16), (33), and (34) are adopted, the following properties are guaranteed:(ⅰ) The states of the closed-loop system are uniformly ultimately bounded. Furthermore, the output tracking errors asymptotically converge to the boundary set.(ⅱ) For the given attenuation level
are positive constants.Theorem 1: Consider the MIMO nonlinear uncertain system (1) and Assumptions 1-3 are satisfied. If the robust adaptive fuzzy control scheme in (24)-(27) with the learning adaptive laws in (16), (33), and (34) are adopted, the following properties are guaranteed:(ⅰ) The states of the closed-loop system are uniformly ultimately bounded. Furthermore, the output tracking errors asymptotically converge to the boundary set.(ⅱ) For the given attenuation level 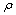 , the tracking performance index (17) is achieved.Proof. Choose Lyapunov function as
, the tracking performance index (17) is achieved.Proof. Choose Lyapunov function as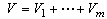
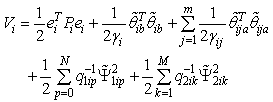 | (35) |
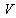 and
and 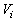 along the solution of (32), we obtain
along the solution of (32), we obtain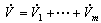
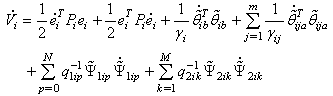 By the fact
By the fact 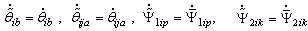 and (14), (25) and (32), the above equation becomes
and (14), (25) and (32), the above equation becomes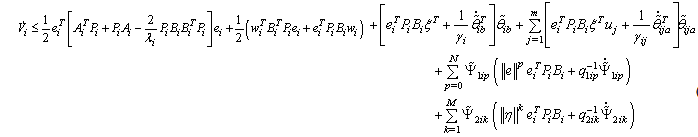 | (36) |
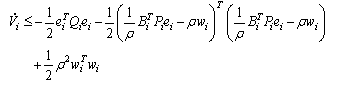 Since
Since 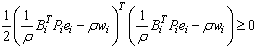
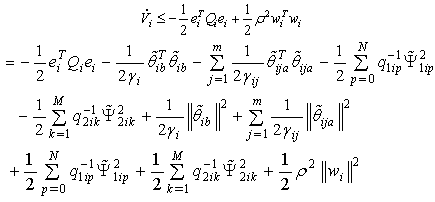 | (37) |
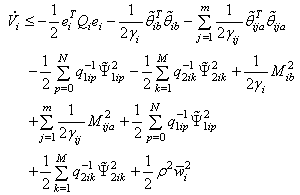 Let
Let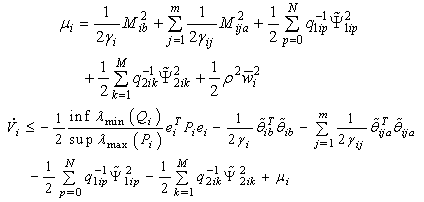 Let
Let 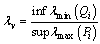
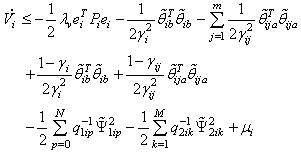 Let
Let 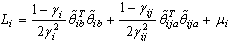
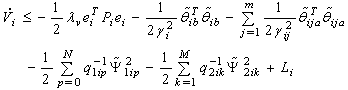 Let
Let 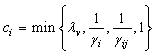
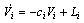 | (38) |
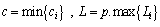 from (35) and (38) we have
from (35) and (38) we have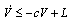 | (39) |
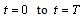 , we have
, we have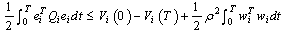 | (40) |
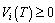 , we can write (40) as follows:
, we can write (40) as follows: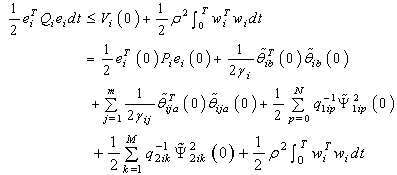 | (41) |
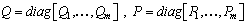
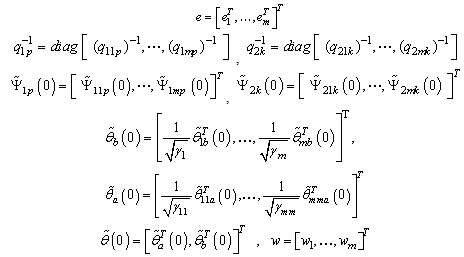 then from (41), we obtain
then from (41), we obtain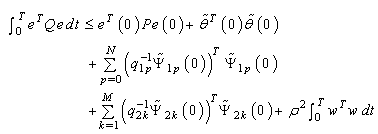 | (42) |
4. An Example and Simulation Results
- In this section we provide an example to demonstrate the performance of the proposed robust adaptive fuzzy controller. The two-degrees-of freedom manipulator[23] shown in Fig.1 is illustrated under the assumption of lumped equivalent masses and mass less links, and its dynamics are represented as follows:
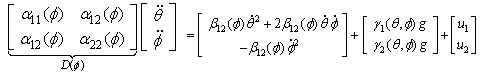 | (43) |
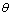 and
and 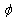 are the first joint angle and the second joint angle, respectively. g is the gravitational constant and
are the first joint angle and the second joint angle, respectively. g is the gravitational constant and 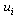 ,
, 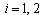 are the applied torques. Suppose that
are the applied torques. Suppose that 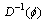 exists and let the desired positions be
exists and let the desired positions be 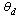 and
and 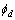 . Let the state vector be defined as
. Let the state vector be defined as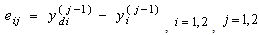
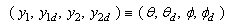 .Equation (43) in state space representation becomes
.Equation (43) in state space representation becomes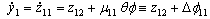 | (44) |
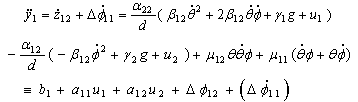 | (45) |
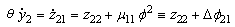 | (46) |
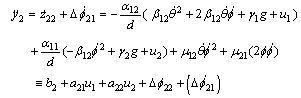 | (47) |
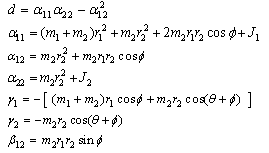 where
where 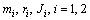 denote the point mass, length of link, and additional constant inertia with respect to axis of rotation. For better comparison to the simulation results of earlier parameter values used are the same as those of[23]:
denote the point mass, length of link, and additional constant inertia with respect to axis of rotation. For better comparison to the simulation results of earlier parameter values used are the same as those of[23]: 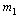 =0.5 kg,
=0.5 kg, 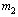 =6.35 kg,
=6.35 kg, 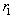 =1 m,
=1 m, 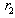 =0.8 m,
=0.8 m, 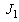 =5 kg-m,
=5 kg-m, 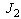 =5 kg-m,
=5 kg-m, 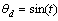
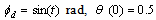 rad. By tracking a sine function, the unmatched uncertainties will be violent change with time varying and raised. This situation could make us more difficult to track the desired output, but the trajectory still can be arrived by the proposed controller in this paper.Choose fuzzy membership functions as follows:
rad. By tracking a sine function, the unmatched uncertainties will be violent change with time varying and raised. This situation could make us more difficult to track the desired output, but the trajectory still can be arrived by the proposed controller in this paper.Choose fuzzy membership functions as follows: 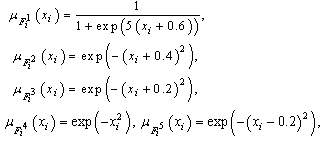
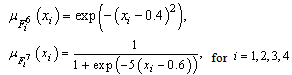 Let
Let 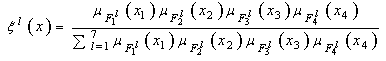 and
and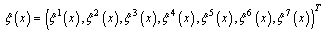 Using (22) and (23) to approximate the unknown
Using (22) and (23) to approximate the unknown  (here we assume
(here we assume 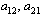 are known a priori). For the
are known a priori). For the 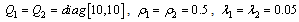 , solving Riccati equation (26), we getLet
, solving Riccati equation (26), we getLet 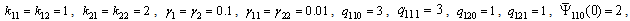
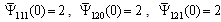 . We set the uncertain coefficients
. We set the uncertain coefficients 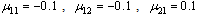 , and
, and 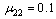 . Results of this simulation are given in Figs 2-6. Figs. 2-3 show the tracking trajectories of joint 1 and joint 2, respectively. Figs. 4-5 show the torques of joint 1 and joint 2, respectively. Fig. 6 shows the curve of the
. Results of this simulation are given in Figs 2-6. Figs. 2-3 show the tracking trajectories of joint 1 and joint 2, respectively. Figs. 4-5 show the torques of joint 1 and joint 2, respectively. Fig. 6 shows the curve of the 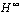 tracking performance index in (17). It is easily shown from these simulation results that the proposed robust adaptive fuzzy control algorithm (24) can achieve the excellent output tracking performances of the nonlinear system with higher-order and unmatched uncertainties.
tracking performance index in (17). It is easily shown from these simulation results that the proposed robust adaptive fuzzy control algorithm (24) can achieve the excellent output tracking performances of the nonlinear system with higher-order and unmatched uncertainties.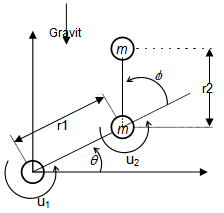 | Figure 1. A two-degree of freedom manipulator |
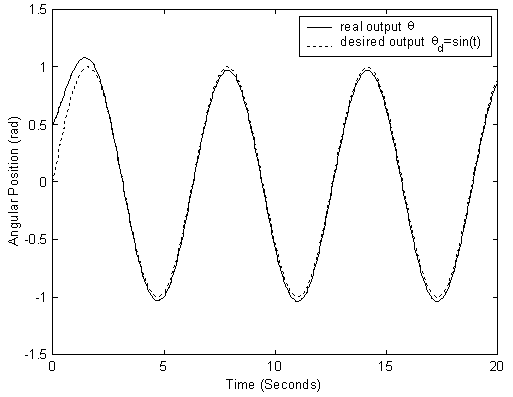 | Figure 2. The tracking trajectory of joint 1 |
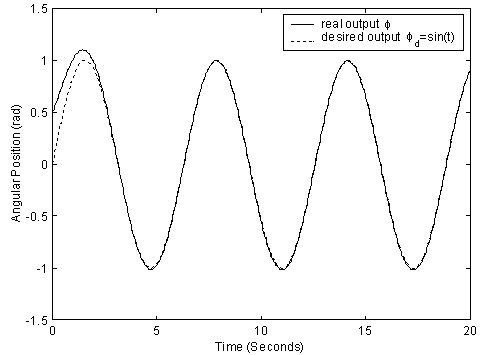 | Figure 3. The tracking trajectory of joint 2 |
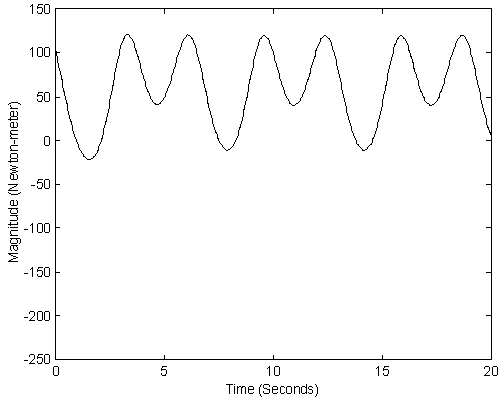 | Figure 4. The torque of joint 1 |
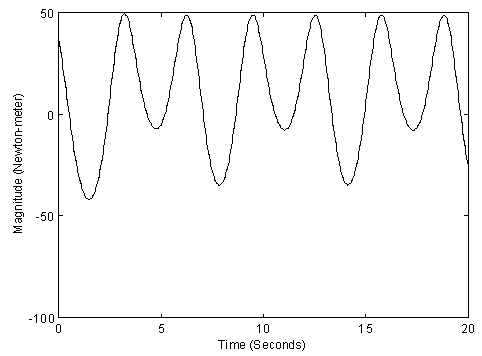 | Figure 5. The torque of joint 2 |
 | Figure 6. Curves of 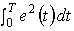 |
5. Conclusions
- The output tracking control problem of MIMO nonlinear systems with higher-order and unmatched uncertainties has been studied in this paper. In the proposed design method, fuzzy logic systems are used to estimate the part of unknown nonlinear functions, and the robust controller that combines the
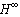 optimal control with adaptive laws can deal with unmatched uncertainties and fuzzy approximation errors. Because of the complexity of the structure of the uncertainties, the upper bounds on the norm of the uncertainties can be estimated by the proposed adaptation laws. Simulation results demonstrate that the overall control system guarantees that all signals involved are uniformly ultimate bounded, and that the tracking performance index can be achieved.
optimal control with adaptive laws can deal with unmatched uncertainties and fuzzy approximation errors. Because of the complexity of the structure of the uncertainties, the upper bounds on the norm of the uncertainties can be estimated by the proposed adaptation laws. Simulation results demonstrate that the overall control system guarantees that all signals involved are uniformly ultimate bounded, and that the tracking performance index can be achieved. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML