-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2012; 2(6): 157-171
doi: 10.5923/j.control.20120206.04
Robust Output Tracking of Uncertain Large-Scale Input-Delay Systems via Decentralized Fuzzy Sliding Mode Control
Chiang-Cheng Chiang
Department of Electrical Engineering, Tatung University, 40 Chung-Shan North Road, Sec.3, Taipei, Taiwan, Republic of China
Correspondence to: Chiang-Cheng Chiang, Department of Electrical Engineering, Tatung University, 40 Chung-Shan North Road, Sec.3, Taipei, Taiwan, Republic of China.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper deals with the robust output tracking problem of uncertain large-scale systems with input delay and the time-delay interconnections. Due to the information transmission between subsystems, time delays are often encountered in large-scale systems and lead to the source of system instability. First, the original nonlinear time-delay systems can be represented by the Takagi-Sugeno fuzzy model, which combines some simple local linear time-delay systems with their linguistic description. Then, a feasible and systematic design scheme is presented to synthesize the decentralized fuzzy-model-based sliding mode controller. The adaptive fuzzy approach is proposed to approximate the upper bound of the uncertainties including the time-delay interconnections and the input delay. Based on the Lyapunov stability theorem, the proposed control scheme can not only guarantee the robust stability of the whole closed-loop system with input delay and time-delay interconnections, but also obtain the good tracking performance. Finally, simulation results are given to confirm the effectiveness of the proposed controller in this paper.
Keywords: Decentralized Control, Large-Scale Systems, Output Tracking, Input Delay, Fuzzy Model, Sliding Mode Control
Cite this paper: Chiang-Cheng Chiang, "Robust Output Tracking of Uncertain Large-Scale Input-Delay Systems via Decentralized Fuzzy Sliding Mode Control", International Journal of Control Science and Engineering, Vol. 2 No. 6, 2012, pp. 157-171. doi: 10.5923/j.control.20120206.04.
Article Outline
1. Introduction
- Recently, there have been a number of research works on stability analysis and design for a class of large-scale interconnected systems, such as electrical networks, nuclear reactors, and hydraulic systems, etc. Due to the large-scale system with interconnected terms, the decentralized controller is preferred to be adopted as a control methodology such that design procedures can be simplified and the computational burden can be shared by all the subsystem controllers[1-5]. In fact, for the complexity of large-scale systems, the uncertainty and time delay are often encountered in these systems. Therefore, the problem of control design and stabilization for a class of large-scale systems with uncertainties and time delays becomes an important topic. In practices, due to the information transmission between subsystems, time delays inevitably occur in large-scale systems. Also, the existence of time delays is often a source of instability in various engineering systems. Therefore, the stabilization problem of large-scale systems with delayed states and the time-delay interconnections has been widely studied in the literature[6-10]. It has been shown that the presence of input delays, if not considered in a controller design, may cause instability or serious deterioration in the performance of the resulting nonlinear control systems [11-14]. In this study, the problem of the decentralized control for a class of input-delayed large-scale systems with the time-delay interconnections is investigated. On the other hand, fuzzy logic control has been successfully applied to the control design of nonlinear control systems[15-18]. It is well-known that fuzzy logic control, which is based on fuzzy sets and fuzzy reasoning with a set of linguistic control rules, does not need a rigorous mathematical model and is more insensitive to plant parameter variations and noise disturbance. It has been shown that the method of T-S fuzzy models, in terms of IF-THEN rules with a linear input-output relation, gives an effective and feasible approach to the control problem of complex nonlinear systems[19-23]. Therefore, in this study, the proposed control scheme is based on the T-S fuzzy model to deal with the control design of uncertain large-scale system with delayed input and time-delay interconnections. Sliding-mode control (SMC) systems have been extensively studied and widely applied to many engineering systems. Due to its good robustness to uncertainties, sliding mode control has proven to be an effective method for robust control of nonlinear systems. In recent literature, some researchers proposed the design methods of fuzzy logic control based on sliding-mode approaches for a class of ill-defined or poorly modelled systems[24-29]. Recently, the stability and control design of large-scale systems has attracted the attention of many control researchers and been studied extensively[30-34]. Wang et al.[33] and Hsiao et al.[34] presented linear state feedback control approaches based on T-S fuzzy model for the large-scale system, respectively. Unlike previous works, this paper is to present a different control scheme to tackle the problem of large-scale systems with delayed input and the time-delay interconnections, without the assumption that the upper bounds of the interconnections and modelling errors must be known. This paper is concerned with the robust stability and output tracking control problem of decentralized fuzzy-model-based sliding mode controller for uncertain large-scale systems with delayed input and the time-delay interconnections. First, in this paper the original nonlinear time-delay large-scale systems can be represented by the Takagi-Sugeno fuzzy model, which combines some simple local linear time-delay systems with their linguistic description. Then, an effective and feasible design scheme is developed to synthesize the proposed decentralized fuzzy-model-based sliding mode controller with some adaptive fuzzy laws to approximate the upper bound of the uncertainties including the time-delay interconnections and the delayed input. Finally, simulation results are given to demonstrate the validity of the proposed controller in this paper. The rest of this paper are organized as follows. In Section 2, some properties of the T-S fuzzy system are reviewed, and the large-scale systems with time delays and uncertainties are formulated in detail. Furthermore, the control design method to synthesize the proposed decentralizedfuzzy-model-based sliding mode controller and the analysis of robust stability are included in Section 3. In Section 4, simulation results are given to verify the effectiveness of the proposed decentralized controller in this paper. At last, a conclusion is given in Section 5.
2. Problem Formulation
- The fuzzy dynamic model, proposed by Takagi and Sugeno, is described by fuzzy IF-THEN rules, which represents local linear input-output relations of nonlinear systems. Let us consider the uncertain input-delayed large-scale systems with time-delay interconnections which can be described by the following fuzzy model:
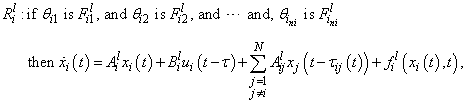 | (1) |
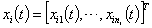 with
with 
 is the manipulated input of
is the manipulated input of  subsystem, the delays
subsystem, the delays 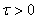 and
and 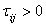 denote the input-delayed and time delay in the interconnections, respectively.
denote the input-delayed and time delay in the interconnections, respectively. 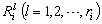 denotes the
denotes the 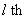 fuzzy inference rule of
fuzzy inference rule of 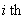 subsystem,
subsystem, 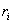 is the number of rules,
is the number of rules, 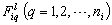 are fuzzy set,
are fuzzy set, 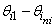 are the premise variables.
are the premise variables. 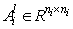 and
and 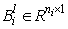 are constant matrices in controllability canonical form and given by
are constant matrices in controllability canonical form and given by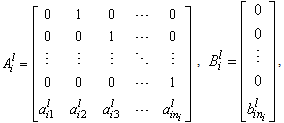 | (2) |
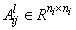 and
and  are defined as follows:
are defined as follows: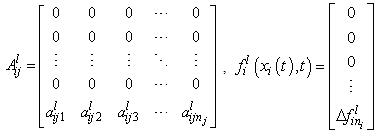 | (3) |
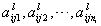 and
and  are unknown.Assumption 1: All pairs
are unknown.Assumption 1: All pairs  ,
,  , are controllable.By using the fuzzy inference method with a singleton fuzzifier, product inference, and center-average defuzzifier, the fuzzy model (1) can be expressed as the following global model:
, are controllable.By using the fuzzy inference method with a singleton fuzzifier, product inference, and center-average defuzzifier, the fuzzy model (1) can be expressed as the following global model: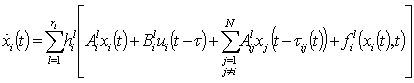 | (4) |
 ,
, 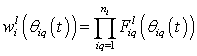 , and
, and 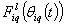 is the grade of membership of
is the grade of membership of  in
in 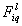 . It is seen that
. It is seen that 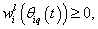
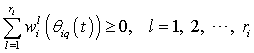 . for all
. for all 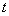 . Therefore,
. Therefore, 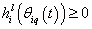 ,
,  , for all
, for all 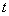 . Accordingly, the main control objective of this paper is to utilize the decentralized fuzzy-model-based sliding mode control
. Accordingly, the main control objective of this paper is to utilize the decentralized fuzzy-model-based sliding mode control  such that the robust stability of the whole closed-loop system with input delay and time-delay interconnections can be guaranteed.
such that the robust stability of the whole closed-loop system with input delay and time-delay interconnections can be guaranteed.3. Decentralized Fuzzy-Model-Based Adaptive Sliding Mode Controller Design
- In this section, the control objective is to design a decentralized fuzzy-model-based sliding mode control scheme such that the desired state trajectory of the closed-loop system is achieved and the effects of system uncertainty can be attenuated while maintaining the boundedness of all signals inside the control loops.Using the T-S fuzzy model (4) of the original system, it can be obtained that
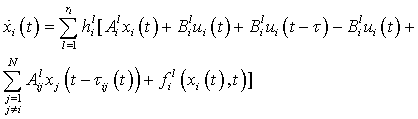 | (5) |
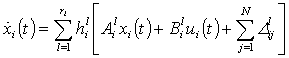 | (6) |
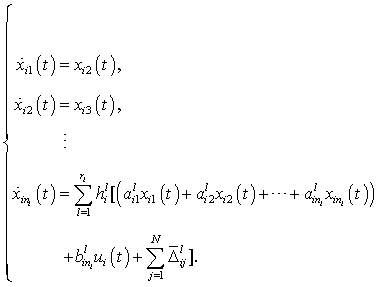 | (7) |
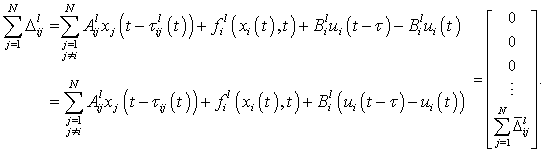 | (8) |
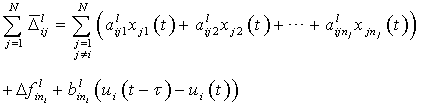 | (9) |
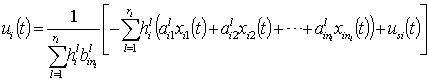 | (10) |
 will be determined in the latter.Substituting (10) into (7), it yields
will be determined in the latter.Substituting (10) into (7), it yields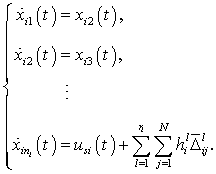 | (11) |
 to track a specific desired state
to track a specific desired state 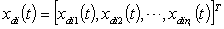 , where
, where  for
for 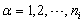 . Assumption 2: The desired state
. Assumption 2: The desired state 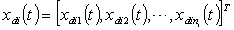 for the
for the 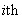 subsystem is continuous and available, and
subsystem is continuous and available, and 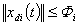 with
with 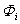 being a known positive bounded constant.Let the tracking error vector of the
being a known positive bounded constant.Let the tracking error vector of the 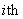 subsystem be defined as
subsystem be defined as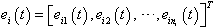 | (12) |
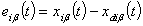 ,
, 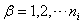 , and
, and  From (6), (9), and (10), the error dynamic system of the
From (6), (9), and (10), the error dynamic system of the 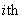 subsystem can be expressed as
subsystem can be expressed as 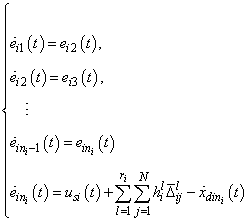 | (13) |
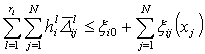 | (14) |
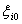 are unknown constants and smooth functions
are unknown constants and smooth functions 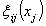 are unknown smooth functions with
are unknown smooth functions with 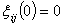 .To solve these situations, we employ an adaptive gain
.To solve these situations, we employ an adaptive gain 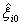 to adapt the unknown constant
to adapt the unknown constant 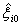 and the fuzzy logic system
and the fuzzy logic system  to approximate unknown functions
to approximate unknown functions 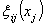 respectively.In this case, we replace
respectively.In this case, we replace 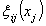 by the fuzzy logic system
by the fuzzy logic system  , where
, where  is the fuzzy system with singleton fuzzifier, center-average defuzzifier, and product inference are the following form:
is the fuzzy system with singleton fuzzifier, center-average defuzzifier, and product inference are the following form: | (15) |
 | (16) |
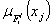 are Triangular membership functions. Then the fuzzy logic system (15) is equivalent to a fuzzy basis function expansion
are Triangular membership functions. Then the fuzzy logic system (15) is equivalent to a fuzzy basis function expansion | (17) |
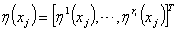 is a regressive vector with the regressor
is a regressive vector with the regressor 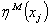 defined as a fuzzy basis function, and
defined as a fuzzy basis function, and  are the corresponding parameter vectors of the fuzzy logic system. Define the optimal parameter vector of fuzzy logic system
are the corresponding parameter vectors of the fuzzy logic system. Define the optimal parameter vector of fuzzy logic system 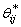 and the minimum approximation error as
and the minimum approximation error as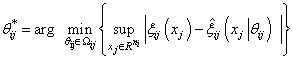 | (18) |
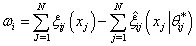 | (19) |
 is the convex compact set, which contain the feasible parameter set for
is the convex compact set, which contain the feasible parameter set for 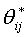 , and
, and 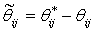 , denotes the parameter estimation error.Then, we adapt minimum approximation error
, denotes the parameter estimation error.Then, we adapt minimum approximation error 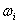 of utilizing the adaptive gain
of utilizing the adaptive gain 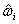 , therefore, we can define adaptation error of minimum approximation error as
, therefore, we can define adaptation error of minimum approximation error as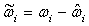 | (20) |
 is defined as
is defined as | (21) |
 , where the sliding surface of each subsystem is selected as the following form:
, where the sliding surface of each subsystem is selected as the following form: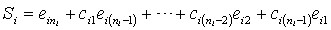 | (22) |
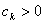 for
for  , and
, and  ,
, 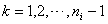 are chosen such that the following polynomial
are chosen such that the following polynomial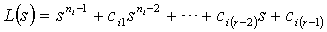 | (23) |
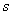 is the Laplace operator. Thus, when the state error trajectories reach the sliding surface
is the Laplace operator. Thus, when the state error trajectories reach the sliding surface  and slide along the surface i.e.
and slide along the surface i.e.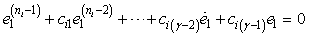 | (24) |
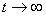 . Based on Assumption 3, we get the decentralized control law as follows:
. Based on Assumption 3, we get the decentralized control law as follows: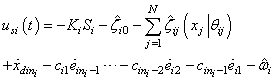 | (25) |
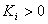 . By taking the time derivative of both sides of (22), we can obtain
. By taking the time derivative of both sides of (22), we can obtain | (26) |
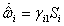 | (27) |
 | (28) |
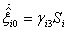 | (29) |
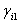 ,
, 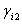 , and
, and  are positive constants specified by the designer. The proposed control law will guarantee the asymptotical stability for the error dynamics of (13), and it will be proved in the following theorem.Theorem 1: For the subsystems consisting of (1), the decentralized fuzzy-model-based sliding mode control law is chosen as (10) with (25), and consider the adaptation laws (27)-(29). If Assumptions 1-3 are satisfied, then the following properties are guaranteed:1). All the signals in the closed-loop system are bounded.2). The tracking error
are positive constants specified by the designer. The proposed control law will guarantee the asymptotical stability for the error dynamics of (13), and it will be proved in the following theorem.Theorem 1: For the subsystems consisting of (1), the decentralized fuzzy-model-based sliding mode control law is chosen as (10) with (25), and consider the adaptation laws (27)-(29). If Assumptions 1-3 are satisfied, then the following properties are guaranteed:1). All the signals in the closed-loop system are bounded.2). The tracking error 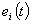 decreases asymptotically to zero.Proof: In order to prove this theorem, we consider the following Lyapunov function:
decreases asymptotically to zero.Proof: In order to prove this theorem, we consider the following Lyapunov function: 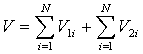 | (30) |
 | (31) |
 | (32) |
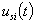 , the sliding surface may be expressed as
, the sliding surface may be expressed as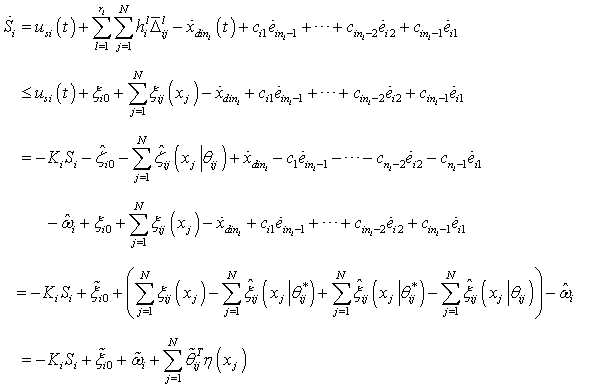 | (33) |
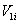 can be stated as follows:
can be stated as follows: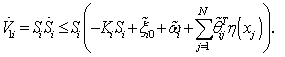 | (34) |
 | (35) |
 , we have
, we have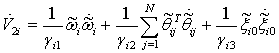 | (36) |
 ,
,  , and
, and 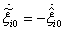 , the above equation becomes
, the above equation becomes | (37) |
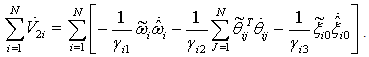 | (38) |
 | (39) |
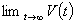 exists, i.e.
exists, i.e.  exists. It is easy to show that
exists. It is easy to show that  exists. Hence, we can obtain that
exists. Hence, we can obtain that | (40) |
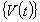 is convergent, from the above analysis we obtain that the solutions
is convergent, from the above analysis we obtain that the solutions  ,
,  ,
, 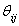 , and
, and 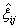 are bound. Because of the boundedness of all the signals, it is obvious from (33) that
are bound. Because of the boundedness of all the signals, it is obvious from (33) that 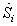 is bounded. From (40) and based on the above discussion, this implies that
is bounded. From (40) and based on the above discussion, this implies that 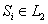 . According to Barbalat’s Lemma[35], we can get
. According to Barbalat’s Lemma[35], we can get 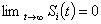 . Then
. Then 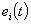 tends to zero at
tends to zero at  . Thus, we conclude that the asymptotic state tracking can be achieved.
. Thus, we conclude that the asymptotic state tracking can be achieved.4. An Example and Simulation Results
- In this example, we consider a large-scale system
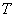 composed of two fuzzy subsystems
composed of two fuzzy subsystems 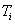 defined asSubsystem 1:Rule 1:
defined asSubsystem 1:Rule 1: Rule 2:
Rule 2: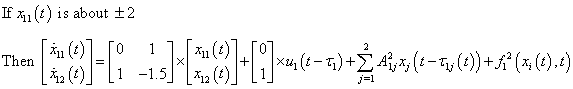 Rule 3:
Rule 3:
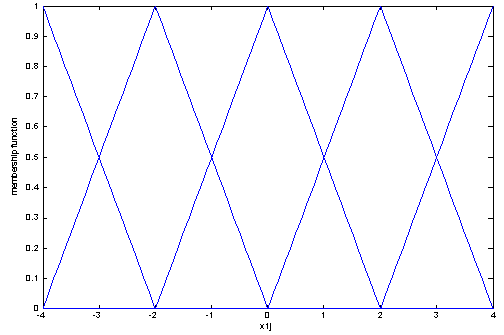 | Figure 1. The membership function of 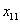 and and 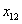 |
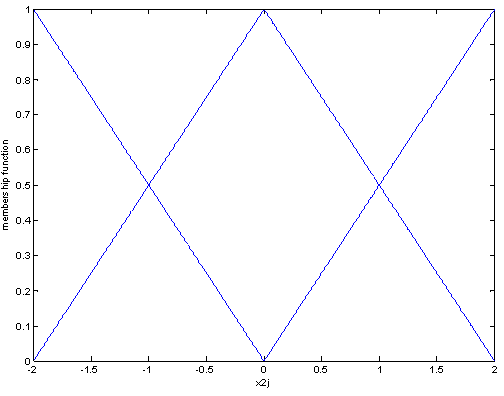 | Figure 2. The membership function of 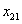 and and 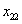 |
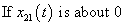
 Rule 2:
Rule 2: The membership functions for
The membership functions for  ,
,  ,
, 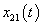 , and
, and  are shown in Figs. 1-2. Moreover, the interconnections and perturbations among two subsystems are given as
are shown in Figs. 1-2. Moreover, the interconnections and perturbations among two subsystems are given as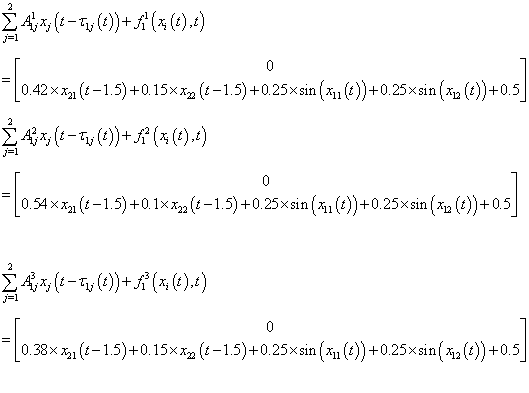
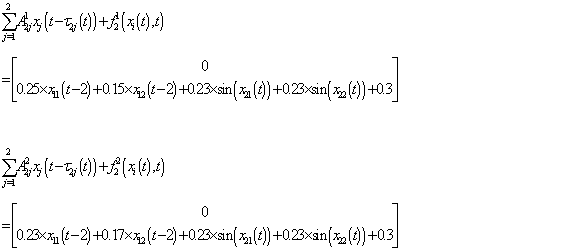
 | Figure 3. Trajectory of the state  and desired state and desired state 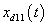 |
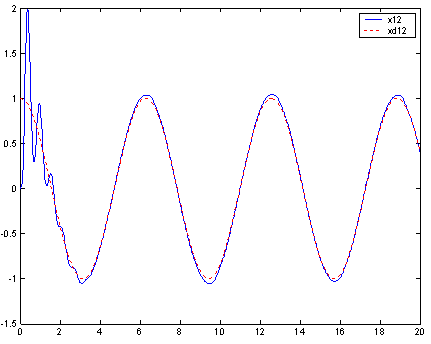 | Figure 4. Trajectory of the state  and desired state and desired state 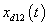 |
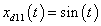 ,
, 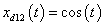 ,
,  , and
, and 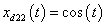 . The control objective is to design a controller
. The control objective is to design a controller 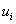 such that the state trajectory
such that the state trajectory 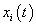 of each subsystem can track the desired state
of each subsystem can track the desired state 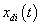 .In accordance with (22), the decentralized switching manifolds for the subsystems are chosen as follows:
.In accordance with (22), the decentralized switching manifolds for the subsystems are chosen as follows: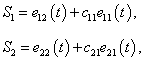 where
where 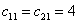 . The initial values are chosen as
. The initial values are chosen as ,
,  ,
, 

 and
and 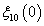
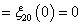 , and
, and 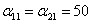 ,
, 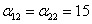 ,
,  , and
, and 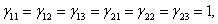 and
and 
 and
and  and
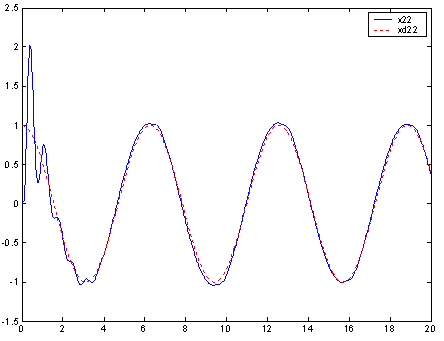
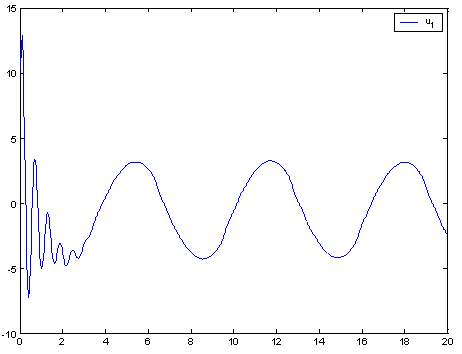
and 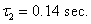 Simulation results are shown in Figs. 3-8. Figs. 3-6 show the trajectories of the states
Simulation results are shown in Figs. 3-8. Figs. 3-6 show the trajectories of the states 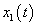 ,
,  and desired states
and desired states 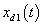 ,
, 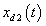 . Fig. 7 and Fig. 8 show the responses of the control laws
. Fig. 7 and Fig. 8 show the responses of the control laws 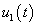 and
and  , respectively.
, respectively. | Figure 5. Trajectory of the state  and desired state and desired state 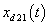 |
 | Figure 6. Trajectory of the state  and desired state and desired state 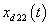 |
 | Figure 7. The control signal  |
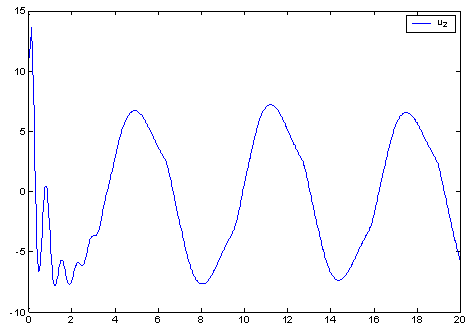 | Figure 8. The control signal 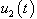 |
5. Conclusions
- The problem of robust stability and output tracking control for a class of uncertain large-scale input-delay systems with time-delay interconnections is investigated in this paper. In addition, a feasible and systematic design method is provided to develop the decentralized fuzzy - model-based adaptive sliding mode controller with some adaptive laws to approximate the upper bounds of the uncertainties including the time-delay interconnections and the delayed input. Based on the Lyapunov stability theorem, the proposed control scheme not only guarantees the robust stability of the whole closed-loop system, but also achieves the good tracking performance. An example and simulation results are illustrated to verify the effectiveness of the proposed controller in this paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML