-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2012; 2(6): 150-156
doi: 10.5923/j.control.20120206.03
Lateral Vehicle Control for Semi-Autonomous Valet Parking with Consideration of Actuator Dynamics
Dohyun Kim, Bongsob Song
Department of Mechanical Engineering,Ajou University, Suwon, 443-749, Korea
Correspondence to: Bongsob Song, Department of Mechanical Engineering,Ajou University, Suwon, 443-749, Korea.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, the lateral control algorithm for semi-autonomous valet parking is presented and its feasibility is demonstrated via field driving tests. With the assumptions of low speed driving and small slip angle, a vehicle model with kinematic constraints of a steering actuator is proposed todesign the lateral controller. A model-based nonlinear control technique called dynamic surface control is applied to developa lateral control law for forward driving and backward parallel parking maneuvers. Furthermore, the previewcontrol and filteringtechniquesare incorporated in the lateral controller to improve the tracking performance. Since there is measurement noiseregarding position and yaw angle and model uncertainty, it is necessary for the proposed lateral controller to be robust enough to compensate for noise and disturbance. Finally the performance of the lateral controller is validated experimentally via field testsas well as simulations.
Keywords: Lateral Control, Semi-autonomous Valet Parking, Parallel Parking, Nonlinear Control
Cite this paper: Dohyun Kim, Bongsob Song, "Lateral Vehicle Control for Semi-Autonomous Valet Parking with Consideration of Actuator Dynamics", International Journal of Control Science and Engineering, Vol. 2 No. 6, 2012, pp. 150-156. doi: 10.5923/j.control.20120206.03.
Article Outline
1. Introduction
- The growing attention has been paid to a parking assistance system (PAS) to provide more safety and convenience to a driver. The PASallows the driver to park a car without manual steering control and has been commercializedrecently by many automakers[1]. Furthermore, the advanced parking assistance system (APAS) (or called self-parking), which makes a vehicle parked autonomously, has been developed[2, 3].For instance, autonomous driving including autonomous valet parking (AVP) was demonstrated in the Urban Challengein 2007, which is an autonomous vehicle competition[4, 5]. Whereas it succeeded in showing the feasibility of autonomous drivingwith many additional sensors such as radars, lidars, cameras, and ultrasonic sensors to recognize lane, obstacles, and a parking lot, it is interesting to remark that the detection range to identify an available parking lot in a public parking structure is still limited.Another approach is to develop an intelligent parking infrastructure whichprovides usefully driving information such as position of the vehicle, obstacles and location of anavailable parking space to either a driver or a vehicle wirelessly via vehicle to infrastructure (V2I) communication. Since a parking guidance system to identify an optimal parking lot and guide the route to the driver has been already developed[6], the development of the intelligent parking infrastructure is feasible if the positions of all vehicles in the parking structure can be measured or estimated.One possible approach to obtain this information is to use a set of infrastructure sensors such as lidars and cameras, which are implemented in the parking structure, not on the vehicle[7]. That is,the infrastructure sensors detect all vehicles within their detection range, and positions of vehicles are estimated by combining all measurements of sensors and location of sensors centrally in an intelligent parking server.In this paper, a semi-autonomous valet parking (SAVP) system with the cooperation of the intelligent parking infrastructure is considered under the assumption that a driver is in a vehicle and the velocity is controlled manually. Only steering control is performed automatically for forward driving to a parking lot and backward parking maneuvers. Furthermore, it is assumed that an optimal parking lot is identified and the corresponding route, i.e., a set of waypoints, is planned by the intelligent parking server, and the corresponding information is sent to the vehicle via V2I communication.Among many challenging problems for SAVP in the area of perception, planning, communication, and control, a lateral control problem is only focused in this paper. More specifically speaking, the challenging control problems to be solved in this paper are summarized as follows:•Both measurement noise (especially in position and heading angle) and model uncertainty are considered.•Various driving maneuvers (e.g., forward driving, temporary stop, and backward parking) need to be conducted in a unified framework of lateral control.•The driving performance should reflect the behavior of a human driver. Thus, the movement of steering is slow enough to satisfy kinematic constraints of a steering actuator.
2. Driving Scenario and Hardware
- As shown in Fig. 1, it is assumed that the driving scenario for SAVP includes a series of driving maneuvers, i.e., forward driving on a straight and curved road (see a waypoint A to B in Fig. 1), temporary stop (at B in the figure), backward parallel parking (B to C in the figure), and complete stop at the waypoint C. Moreover, it is assumed that an available parking location is determined by an SAVP server which monitors all vehicles in a dedicated intelligent parking infrastructure. Then, the corresponding waypoints (refer to the circles in Fig. 1) are delivered to the vehicle controller via V2I communications.
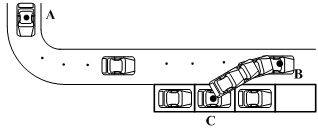 | Figure 1. Driving Scenario for SAVP |
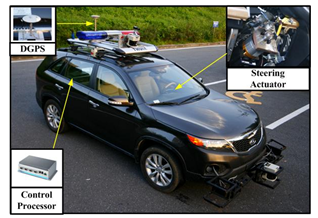 | Figure 2. Hardware Layout of Test Vehicle |
3. Lateral Control
- The lateral controller to provide the desired steering wheel angle for SAVP needs both trajectory for different driving maneuvers and control laws. A kinematic vehicle model subject to kinematic constraints of the steering actuator is proposed and the model-based nonlinear control technique is applied for the controller design.
3.1. Trajectory Generation
- To perform different driving maneuvers such as forward driving and backward parallel parkingas illustrated in Fig. 1, the corresponding trajectory is necessary for the lateral controller. Three approaches for the trajectory generation have been found mainly in the literature: a combination of lines and circles[8, 9], curve fitting[10], and clothoids[11]. In this section, both the combination of circles and curve fitting techniques are used for trajectory generation.In the case of forward driving, the trajectory generation is interpreted as curve interpolation between two given waypoints. Suppose two waypoints are given as p0 (or a point A) and p3 (or a point B) as seen in Fig. 3. Ifa cubic Bezier curve interpolation approach is appliedwith two additional control points, p1 and p2, the trajectory for the forward driving isdetermined as follows:
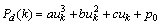 | (1) |
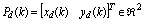 is the desired trajectory(or a set of reference points) between two waypoints with respect to a local coordinate originated at p0,
is the desired trajectory(or a set of reference points) between two waypoints with respect to a local coordinate originated at p0, 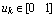 is equally spacing for
is equally spacing for 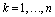 , and the vectors a, b, and c are defined as
, and the vectors a, b, and c are defined as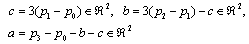 The shape and smoothness of the trajectory in (1) depends on the selection of two control point points(see p1 and p2 in Fig. 3). The control points are written in the coordinate from as follows:
The shape and smoothness of the trajectory in (1) depends on the selection of two control point points(see p1 and p2 in Fig. 3). The control points are written in the coordinate from as follows: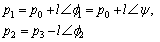 | (2) |
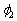 is the angle between p3 and next waypoint. However, it is noted that
is the angle between p3 and next waypoint. However, it is noted that 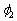 is a predefined angle when the vehicle reaches the waypoint where the parking maneuver begins (refer to a waypoint B in Fig. 3).For the backward parallel parking, one of the simplest trajectory generation techniques is to use two circles based on Ackermann steering geometry of the vehicle[6]. When the vehicle arrives at an available parking location, i.e., near a waypoint Bin Fig. 3, it is assumed that a parking end point, i.e., a waypoint C in Fig. 3, is given via V2I communication.To generate two circles for parallel parking, an intersection point of two circles, Q in Fig. 3, is first calculated under the assumption that two circles with the same radius are used. Since a circle is uniquely determined when two points on the circle are known, a center and radius of the circle passing a current position near a waypoint B and Q can be determined as follows:
is a predefined angle when the vehicle reaches the waypoint where the parking maneuver begins (refer to a waypoint B in Fig. 3).For the backward parallel parking, one of the simplest trajectory generation techniques is to use two circles based on Ackermann steering geometry of the vehicle[6]. When the vehicle arrives at an available parking location, i.e., near a waypoint Bin Fig. 3, it is assumed that a parking end point, i.e., a waypoint C in Fig. 3, is given via V2I communication.To generate two circles for parallel parking, an intersection point of two circles, Q in Fig. 3, is first calculated under the assumption that two circles with the same radius are used. Since a circle is uniquely determined when two points on the circle are known, a center and radius of the circle passing a current position near a waypoint B and Q can be determined as follows: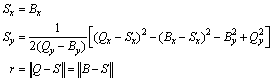 Since the center of the second circle, T, can be obtained similarly, the trajectory for the parallel parking can be summarized as follows:
Since the center of the second circle, T, can be obtained similarly, the trajectory for the parallel parking can be summarized as follows: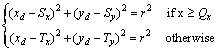 | (3) |
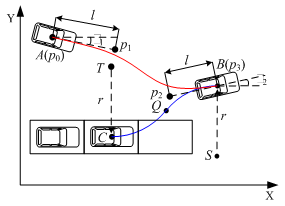 | Figure 3. TrajectoryGeneration for SAVP |
3.2. Vehicle Model
- A bicycle model has been used widely for design of the lateral controller for highway driving[12]. It is assumed that all system parameters of tire stiffness are known and all wheel angles are small. However, a large amount of wheel angle is generated for parking and it is not easy to identify the system parameters for various types of vehicles.For the SAVP, the vehicle is driving at low speed and thus sideslip angle is neglected in this study. Thus, the kinematic model can be used for both driving and parallel parking.The equation of motion is written as follows[13, 14]:
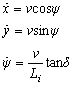 | (4) |
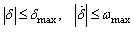 | (5) |
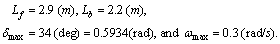 The time responses of the vehicle model in (4) and (5) are compared with experimental data using a test vehicle shown in Fig. 2. The vehicle is driven forward manually from 0 to about 75 second, stopped temporarily to changegear engagement for backward driving, and driven backward from about 78 to 110 second (see the first plot in Fig. 4). The corresponding steering angle is shown in the second plot of Fig. 4. Around 78 second, the maximum steering angle is required for backward parking and the maximum angular velocity of the steering angle is shown at that time. The angular velocity is approximated by use of difference of the steering angle of five samples as follows:
The time responses of the vehicle model in (4) and (5) are compared with experimental data using a test vehicle shown in Fig. 2. The vehicle is driven forward manually from 0 to about 75 second, stopped temporarily to changegear engagement for backward driving, and driven backward from about 78 to 110 second (see the first plot in Fig. 4). The corresponding steering angle is shown in the second plot of Fig. 4. Around 78 second, the maximum steering angle is required for backward parking and the maximum angular velocity of the steering angle is shown at that time. The angular velocity is approximated by use of difference of the steering angle of five samples as follows: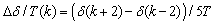 Where T is a sampling time.When the same velocity and steering angle satisfying the constraints in (5) are assigned, it is shown in the fourth and fifth plots of Fig. 4 that both responses of forward driving and backward parking are quite similar with the maximum error deviation of 0.11(rad) and 0.01(rad/s) in terms of the yaw angle and rate respectively
Where T is a sampling time.When the same velocity and steering angle satisfying the constraints in (5) are assigned, it is shown in the fourth and fifth plots of Fig. 4 that both responses of forward driving and backward parking are quite similar with the maximum error deviation of 0.11(rad) and 0.01(rad/s) in terms of the yaw angle and rate respectively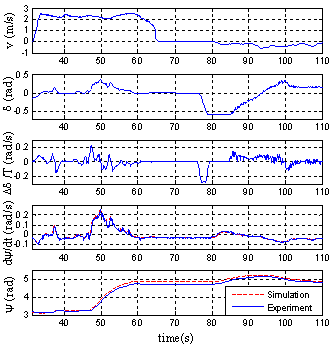 | Figure 4. Comparisonbetween Vehicle Model and ExperimentalData |
3.3. Lateral Control Law
- A model-based nonlinear control technique called dynamic surface control is applied to design alateral controllerat most of speed range[14, 15].First, the error surface is defined as follows (see also in Fig. 5)[14]:
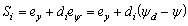 | (6) |
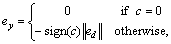 | (7) |
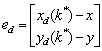 Where k* is obtained iteratively by
Where k* is obtained iteratively by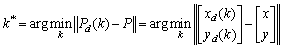 andPd comes from (1) for forward driving and (3) backward parking respectively. Furthermore, the sign of the lateral error in (7) is defined as follows:
andPd comes from (1) for forward driving and (3) backward parking respectively. Furthermore, the sign of the lateral error in (7) is defined as follows: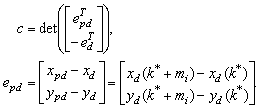 Where [xpdypd]T is the preview point and mi is a constant but two different values are assigned for forward driving and backward parking. When the vehicle is placed as in Fig. 5, c is negative and the lateral error in (7) becomes positive. Then, the positive (or counterclockwise) steering angle command will be determined by the lateral control law which will be discussed later. Furthermore, di and ψd in (6) are defined as
Where [xpdypd]T is the preview point and mi is a constant but two different values are assigned for forward driving and backward parking. When the vehicle is placed as in Fig. 5, c is negative and the lateral error in (7) becomes positive. Then, the positive (or counterclockwise) steering angle command will be determined by the lateral control law which will be discussed later. Furthermore, di and ψd in (6) are defined as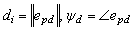 It is noted that the preview control idea is incorporated with DSC by considering both di andψd in (6)[8].After differentiating Si in (6) and combining it with (4), the time derivative of Si is
It is noted that the preview control idea is incorporated with DSC by considering both di andψd in (6)[8].After differentiating Si in (6) and combining it with (4), the time derivative of Si is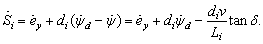 | (8) |
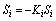 where Ki is acontroller gain. Then the desired steering angle is obtained as
where Ki is acontroller gain. Then the desired steering angle is obtained as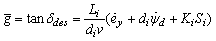 | (9) |
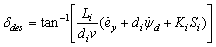 | (10) |
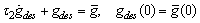 | (11) |
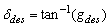 | (12) |
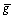 in (9) rather thanδdes in (10) is filtered and it allows us to analyze the stability more easily and clearly[15]. For the second case, since the velocity is controlled manually by a driver, it can be very low or even zero. In this case, the desired steering angle in (10) becomes greater than δmax, thus resulting in saturation of the actuator regardless of the lateral error or Si in (6). Thus, two control laws are switched depending on velocity, i.e., a proportional controller is used when the velocity is very low. Otherwise, the lateral control law in (12) is used. Finally, the modified lateral control law is summarized as follows:
in (9) rather thanδdes in (10) is filtered and it allows us to analyze the stability more easily and clearly[15]. For the second case, since the velocity is controlled manually by a driver, it can be very low or even zero. In this case, the desired steering angle in (10) becomes greater than δmax, thus resulting in saturation of the actuator regardless of the lateral error or Si in (6). Thus, two control laws are switched depending on velocity, i.e., a proportional controller is used when the velocity is very low. Otherwise, the lateral control law in (12) is used. Finally, the modified lateral control law is summarized as follows: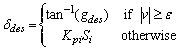 | (13) |
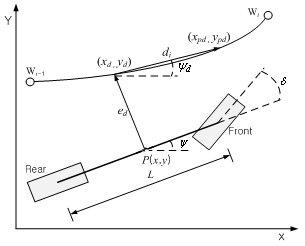 | Figure 5. Definitions of Lateral Error and Heading Angle Error |
4. Validation Results
- Suppose 21 waypoints are given as shown in Fig 6. The forward driving is required from the first to 20th waypoint (A to B in the figure) and the backward parallel parking is asked from 20th to 21st waypoint (B to C in the figure). The proposed lateral controller is validated via a vehicle simulator called CarSim[16] and field tests using a test vehicle shown in Fig. 2.First, the tracking performance of the lateral control law in (13) is validated via simulations with considerations of measurement noise and kinematic constraints of a steering actuator. Before evaluating the performance, it is shown in Fig 6 that trajectory for forward driving and backward parallel parking is generated appropriately. When measurement noise of position and yaw angle is not considered, the performance of the lateral controller in (10) is shown in Fig. 6 and 7. It is validated in Fig. 7 that two different driving maneuvers can be conducted by the single lateral controller with the maximum lateral error deviation of about 0.2 (m) (see the top plot in Fig. 7). However, it is shown in the bottom plot of Fig 7 that the steering angle does not track the desired steering angle sometimes due to the kinematic constraint of the steering angular velocity. If the control law in (13) is used, it is shown in Fig. 8 that the desired steering angle does not violate the kinematic constraints much less than one in (10) without any performance degradation in the term of lateral error.
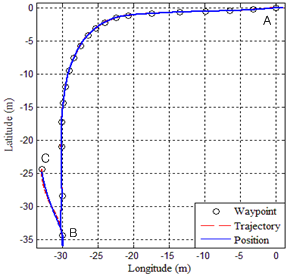 | Figure 6. Waypoint, Trajectory, and Position of Vehicle |
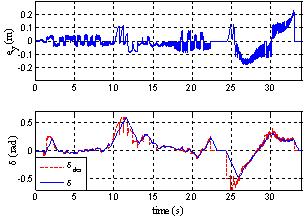 | Figure 7. Time Responses of Lateral Error and Steering Angle without Consideration of Noise |
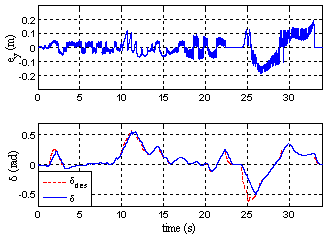 | Figure 8. Time Responses of Lateral Error and Steering Angle of the Modified Lateral Controller |
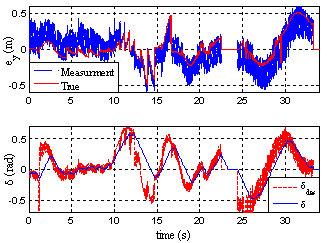 | Figure 9. Time Responses of Lateral Error and Steering Angle with Consideration of Measurement Noise |
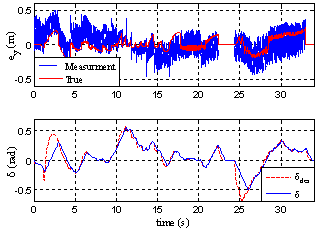 | Figure 10. Time Responses of Lateral Error and Steering Angle of the Modified Lateral Controller |
 | Figure 11. Snapshot of Vehicle Simulation for Forward Driving |
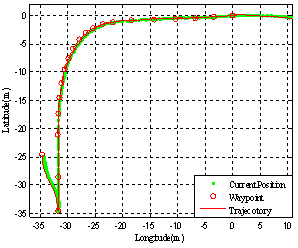 | Figure 12. Position of Lateral Controller in Field Test |
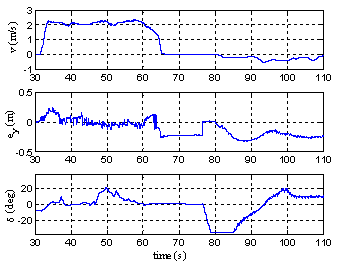 | Figure 13. Time Responses of Lateral Controller in Field Test |
 | Figure 14. Snapshots of Field Test |
5. Conclusions
- The lateral vehicle control algorithmbased on the vehicle model with kinematic constraints of the steering actuator was proposed. It was incorporated with the preview control, switching of multiple controllers, and filtering of the steering command to compensate for performance degradation due to measurement noise and manual control of velocity.Finally, it was validated via simulations and field tests that the proposed controller could be applied to conduct two different driving maneuvers,i.e., forward driving and parallel backward parking. In the near future, it is necessary to consider more various parking maneuvers such as perpendicular and/or multi-step parking, forward parking, and effect of time delay and packet loss when V2I communication is used.
ACKNOWLEDGEMENTS
- This research was supported by the Industrial Strategic Technology Development Program (10035250, Development of Spatial Awareness and Autonomous Driving Technology for Automatic Valet Parking) funded by the Ministry of Knowledge Economy (MKE, Korea).
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML