Hossein Babaee, Alireza Khosravi
Babol University of Technology, Iran
Correspondence to: Hossein Babaee, Babol University of Technology, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper the design of optimized robust iterative learning control (ILC) for the purpose of output tracking is investigated. The main features of the design are that: The control signal is continuous and the coefficient of controller is optimized. Therefore it is chattering-free compared with the robust ILC using classical first-order sliding mode technique. In the proposed system, free parameters of controller have vital role in the performance of system. Therefore we suggest cuckoo optimization algorithm (COA) for finding the best value of these parameters. The continuous and non-chattering control signal can prevent actuators from being damaged. This cannot be realized by the discontinuous and chattering control inputs if the conventional sliding-mode control is applied. An illustrative example is presented to demonstrate the effectiveness of the proposed second order continuous sliding mode ILC.
Keywords:
Multi-objective Optimization, COA, Sliding Mode ILC, Robust Controller
Cite this paper:
Hossein Babaee, Alireza Khosravi, "Multi-objective COA for Design Robust Iterative Learning Control via Second-Order Sliding Mode", International Journal of Control Science and Engineering, Vol. 2 No. 6, 2012, pp. 143-149. doi: 10.5923/j.control.20120206.02.
1. Introduction
Iterative learning control (ILC) is to use the respective action to improve the system performance, particularly output tracking performance without seeking accurate system model knowledge. Conventionally, ILC is to steer system output to track the desired one while rejecting periodic disturbances via repetitive trails. In the other words, ILC is a robust control scheme that can suppress the effect of disturbances on system performance.The classical research regarding robust ILC is presented in[1] where the effects of state disturbances, initial errors and output noise on a class of learning algorithm are investigated. The presented learning algorithm exhibits the bounds on asymptotic trajectory error for the learning input and the corresponding state and output trajectories.In recent years, various robust ILC scheme have been addressed. A nonlinear learning control scheme was developed in[2] by integrating iterative learning and adaptive robust control scheme for nonlinear systems. The main purpose of paper[3] is to provide ILC designer with guidelines to select the learning gains to achieve arbitrary high precision of output tracking regardless of measurement error. In[4], a robust ILC problem for a class of nonlinear systems with structured periodic and unstructured a periodic uncertainties is addressed. The back stepping idea is proposed to design the robust ILC systems. More research papers related to this topic can be found in[5- 9]. Particularly, a robust ILC synthesizing learning control and sliding mode technique with the help of Lyapunov direct method is proposed in[9]. The learning control is applied to the structured uncertainties while the variable structure scheme is to handle the unknown unstructured uncertainties to ensure the global asymptotic stability. Another similar work is suggested in[9] where a learning variable structure control is formalized by combining variables structure control, as the robust part, and learning control, as the intelligent part. The proposed LVSC system achieves both uniform convergence of the tracking-error sequence to zero and the convergence of the learning control sequence to the equivalent control. In aforementioned two research papers, to avoid the undesired chattering of a traditional sliding mode control (SMC), continuous approximations, using saturation function, is employed to reduce the chattering caused by the signum function. The problem is that once the error signals excess the designated boundary layer, a signum function is back to be in charge of the control action. Hence, the saturation function itself can reduce the chattering to an extent that when the tracking –error signal is within the boundary, the control signal is continuous. In short, the saturation function cannot eliminate the chattering completely. Therefore, the adopted variable structure schemes are essential first-order sliding mode measures that inevitably causes chattering though a saturation function has been used to replace the signum function. The actuator, however, cannot respond sometimes to the chattering input signals, let alone the possible damage caused by the discontinuous and the chattering input signals.Higher-order sliding mode is a quality idea to hide the discontinuity of control in its higher derivatives. It turns out to be of enhanced accuracy and robustness to disturbances[9]. In other words, compared with the saturation SMC via second-order sliding mode technique will require less amount of control to maintain the operation on region of convergence due to noises and disturbances.This paper is to suggest a continuous robust ILC using second-order sliding mode technique so that the chattering of control signal can be eliminated eventually. The continuous robust ILC can be applied broadly without damaging actuation device. As mentioned, in continuous robust ILC, free parameters of controller have vital role in the performance of system. Therefore we suggest cuckoo optimization algorithm (COA) for finding the best value of these parameters.This paper is organized as follow: in section two, the considered nonlinear system is illustrated. In section three, COA and proposed method are described. In section four, illustrative example is employed to demonstrate the effectiveness of the proposed chattering free robust ILC. At least concluding remarks are made in section five.
2. Preliminaries
Consider the following higher-order single-input and single output nonlinear dynamical system described by 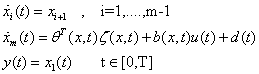 | (1) |
Where the measurable system state 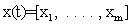 ,
, 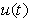 and
and 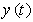 are the control input, respectively,
are the control input, respectively, 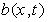 is unknown non-zero function,
is unknown non-zero function, 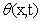 is a
is a 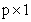 unknown and time varying function to be learnt,
unknown and time varying function to be learnt, 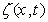 is known vector-valued function with dimension of
is known vector-valued function with dimension of 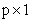 . The variable
. The variable 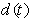 represent the unknown disturbance.Assumption 1: The desired output trajectory
represent the unknown disturbance.Assumption 1: The desired output trajectory 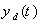 is differentiable with respect to time
is differentiable with respect to time 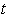 up to the mth order on a finite time interval[0, T], and all of the higher- order derivatives are available. Assumption 2: The unknown disturbance variable
up to the mth order on a finite time interval[0, T], and all of the higher- order derivatives are available. Assumption 2: The unknown disturbance variable 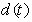 is bounded such that
is bounded such that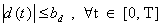 Where
Where 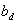 is a known constant.Assumption 3: The initial condition
is a known constant.Assumption 3: The initial condition 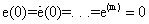 at any iteration
at any iteration 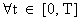 , such that the switching surface
, such that the switching surface 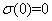 , where
, where 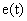 is the output tracking error that is defined as
is the output tracking error that is defined as 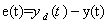 .The control objective is to design a continuous second-order sliding-mode iterative learning controller
.The control objective is to design a continuous second-order sliding-mode iterative learning controller 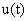 for the uncertain nonlinear system (1) such that system output can follow a desired one with a prescribed accuracy
for the uncertain nonlinear system (1) such that system output can follow a desired one with a prescribed accuracy 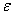 as follow:
as follow: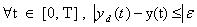
3. Main Results
The underlying robust ILC is to learn and approach the unknown state-dependent function and leave the remaining unknown function to the robust control. The global asymptotic convergence with respect to iteration is established by lyapunov direct method.A. Switching surface For the considered system (1), a switching surface is defined as follow: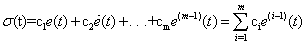 | (2) |
Where 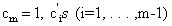 are coefficients of a Hurwitz polynomial, and
are coefficients of a Hurwitz polynomial, and 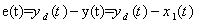 . Taking derivatives with respect to time
. Taking derivatives with respect to time 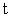 on both sides of (2), it is obtained:
on both sides of (2), it is obtained: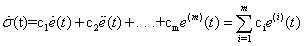 | (3) |
Considering the fact that the above equation can be further expanded: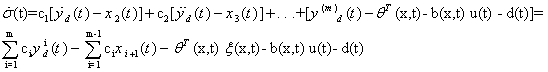 | (4) |
The above equation can be further interpreted as the sliding variable dynamics. The condition, 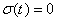 ,defines the system motion on the sliding surface. The control signal
,defines the system motion on the sliding surface. The control signal  is to be designed as an iterative and continuous control input signal. The task of this work is to design such a continuous and iterative control input to steer the sliding surface in finite time interval.B. Robust ILC using Continuous Second-order Sliding ModeIn[10, 11], the second-order sliding-mode concept is originated. It is further developed in[12]. In reference to this work, the proposed continuous second-order sliding-mode ILC at kth iteration is designed as follow:
is to be designed as an iterative and continuous control input signal. The task of this work is to design such a continuous and iterative control input to steer the sliding surface in finite time interval.B. Robust ILC using Continuous Second-order Sliding ModeIn[10, 11], the second-order sliding-mode concept is originated. It is further developed in[12]. In reference to this work, the proposed continuous second-order sliding-mode ILC at kth iteration is designed as follow: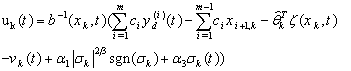 | (5) |
Where 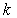 indicate the number of iteration,
indicate the number of iteration, 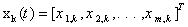 ,
,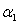 and
and 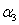 are positive constant.
are positive constant. 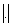 is the absolute value,
is the absolute value, 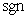 is the signum function,
is the signum function, 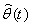 is the recursive control part that is used to learn the unknown function
is the recursive control part that is used to learn the unknown function 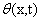 and generate by the following update law:
and generate by the following update law: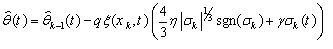 | (6) |
Where 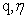 and
and 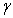 are positive constants.The variable
are positive constants.The variable 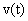 is an integral term that is defined below:
is an integral term that is defined below: 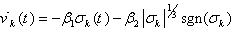 | (7) |
Where 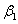 and
and 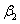 are positive constant.Controller (5), together with (6) and (7), defines the continuous second-order sliding-mode ILC.
are positive constant.Controller (5), together with (6) and (7), defines the continuous second-order sliding-mode ILC.
4. Proposed Method (COA-ILC)
4.1. Cuckoo Optimization Algorithm (COA)
In nature, animals search for food in a random or quasi- random manner. In general, the foraging path of an animal is effectively a random walk because the next move is based on the current location/state and the transition probability to the next location. Which direction it chooses depends implicitly on a probability which can be modeled mathematically. COA is a metaheuristic search algorithm which has been proposed recently by R. Rajabioun[13]. The algorithm is inspired by the reproduction strategy of cuckoos. Like other evolutionary algorithms, the COA starts with an initial population of cuckoos. These initial cuckoos have some eggs to lay in some host birds’ nests. Some of these eggs which are more similar to the host bird’s eggs have the opportunity to grow up and become a mature cuckoo. Other eggs are detected by host birds and are killed. The grown eggs reveal the suitability of the nests in that area. The more eggs survive in an area, the more profit is gained in that area. So the position in which more eggs survive will be the term that COA is going to optimize.Cuckoos search for the most suitable area to lay eggs in order to maximize their eggs survival rate. After remained eggs grow and turn into a mature cuckoo, they make some societies. Each society has its habitat region to live in. The best habitat of all societies will be the destination for the cuckoos in other societies. Then they immigrate toward this best habitat. They will inhabit somewhere near the best habitat. Considering the number of eggs each cuckoo has and also the cuckoo’s distance to the goal point (best habitat), some egg laying radii is dedicated to it. Then, cuckoo starts to lay eggs in some random nests inside her egg laying radius. This process continues until the best position with maximum profit value is obtained and most of the cuckoo population is gathered around the same position. More details regarding the COA can be found in[13].
4.2. COA-ILC
In the proposed method the most important parameters of ILC are selected using COA. In this method mean square error and minimum iteration are considered as fitness function. Indeed we are faced with multi-objective problem. Eq. 7 illustrates the fitness function.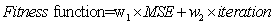 | (7) |
Also, Fig. 1 shows the sample cuckoo. Fig. 2 shows the flowchart of proposed method. 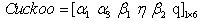 | Figure 1. Sample cuckoo |
5. Simulation Results
Consider the following robotic manipulator example borrowed from[14].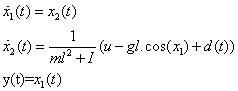 | (8) |
Where 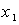 is the joint angle,
is the joint angle, 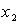 is the angular velocity,
is the angular velocity, 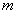 is the mass,
is the mass, 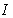 is the moment of inertia,
is the moment of inertia, 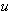 is the joint point and
is the joint point and 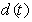 is a disturbance being
is a disturbance being 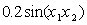 .Further the system output is
.Further the system output is 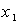 and the desired output trajectory is
and the desired output trajectory is 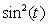 . The parameters take the values:
. The parameters take the values: 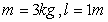 and
and 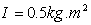 .Inserting the parameter values, (8) have an alternative form:
.Inserting the parameter values, (8) have an alternative form: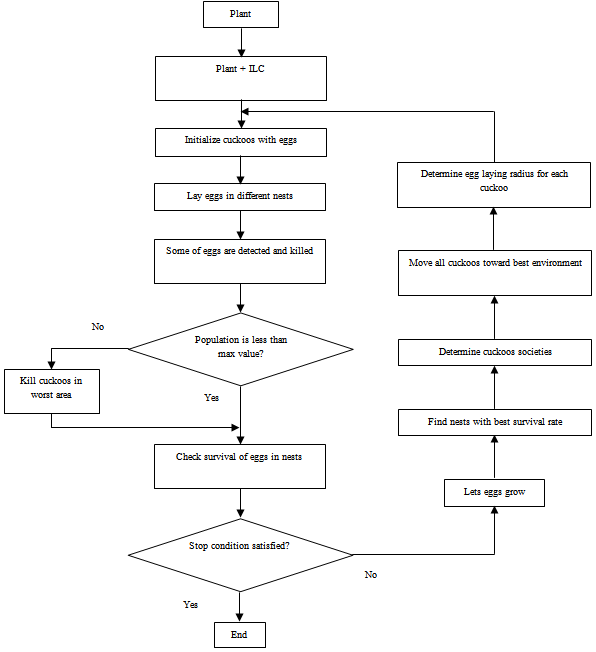 | Fiure 2. Flowchart of proposed method |
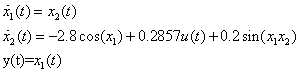 | (9) |
Comparing the above system with the considered system (1), we obtain: 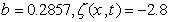 and
and 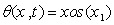 which is assumed unknown and to be learnt. Following (2), a switching surface is designed as:
which is assumed unknown and to be learnt. Following (2), a switching surface is designed as: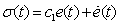 | (10) |
Where 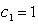 and
and 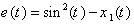 . Taking derivative on the above switching surface yields:
. Taking derivative on the above switching surface yields: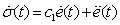 | (11) |
The proposed robust ILC can be designed as follow: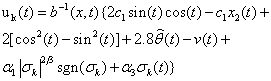 | (12) |
5.1. Performance without Optimization
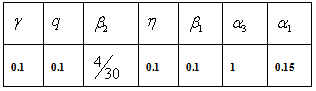
Table 1 shows the parameters of ILC. These values obtained with trial and error.We first of all test the ILC with the number of trials being 50. The output-tracking errors at 5th , 20th, 30th, and 50th trials are shown in Fig. 3 through 5 where the red lines are the desired trajectory while the blue lines are the actual system output.Table 1. Parameters of ILC without optimization
 |
| |
|
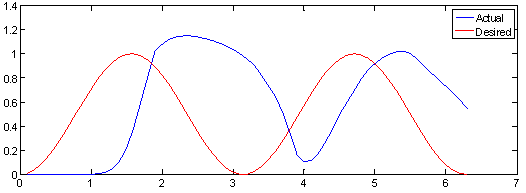 | Figure 3. System output and desired trajectory at 5th iteration (Without optimization) |
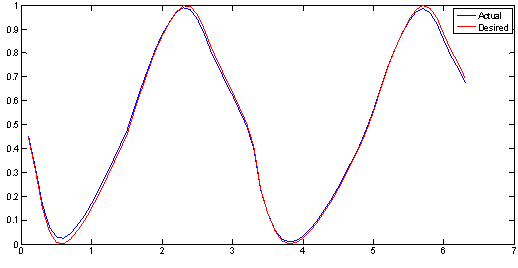 | Figure 4. System output and desired trajectory at 20th iteration (Without optimization) |
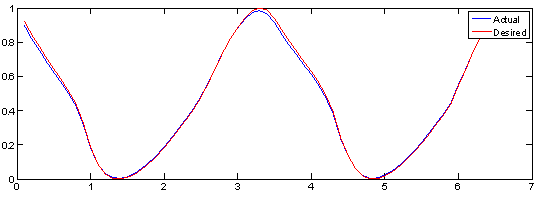 | Figure 5. System output and desired trajectory at 50th iteration (Without optimization) |
5.2. Performance with Optimization
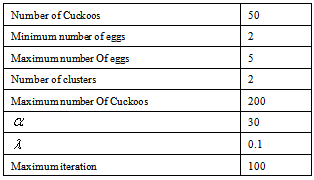
Table 2. Coefficient values in the COA
 |
| |
|
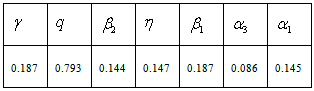
Next, we apply COA to find the optimum parameters of the ILC. Table 2 shows the COA parameters. These values obtained after several experiments. Table 3 shows the best results for ILC parameters. We first of all test the ILC with the number of trials being 50. The output-tracking errors at 5th, 20th, 30th, and 50th trials are shown in Figs. 7 through 9 where the red lines are the desired trajectory while the blue lines are the actual system output. Obtained results show that optimization significantly improve the accuracy of the system.Table 3. Parameters of ILC with optimization
 |
| |
|
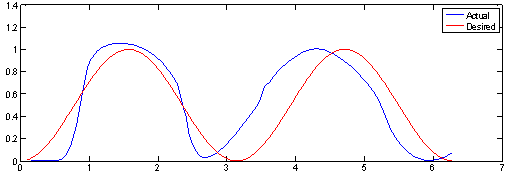 | Figure 6. System output and desired trajectory at 5th iteration (With optimization) |
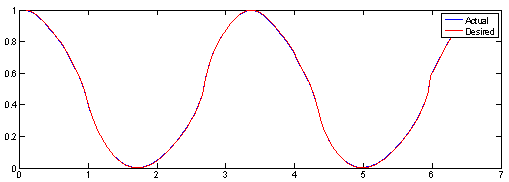 | Figure 7. System output and desired trajectory at 20th iteration (Without optimization) |
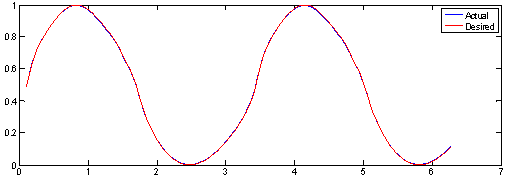 | Figure 8. System output and desired trajectory at 50th iteration (Without optimization) |
6. Conclusions
This paper proposed a optimized continuous robust iterative learning control strategy for class of nonlinear system for the purpose of output tracking. The insight of chattering –free design is the employment of the second –order sliding mode technique that can completely remove the discontinuity of the control signal. In this system the free parameters of ILC have vital role in the performance of the system. Therefore we propose COA to find the best values of these parameters. Simulation results show that proposed method has high performance.
References
| [1] | G. Heinzinger, D. Fenwick, B. Paden and F. Miyazaki. Stability of learning control with disturbances and uncertain initial conditions. IEEE Trans Auto. 31 (1999) 110-114 |
| [2] | J. X. Xu and B. Viswanathan. Adaptive robust iterative learning control with dead zone scheme. Automatica 36 (2000) 91-99 |
| [3] | S. S. Saab. Selection of the learning gain matrix of an iterative learning control algorithm in presence of measurement noise. IEEE Trans Auto. 50 (2005) 1761-1774 |
| [4] | Y. Tian and H. Yu. Robust learning control for class of nonlinear system with periodic and aperiodic uncertainties. Automatica 39 (2003) 1957- 1966 |
| [5] | D. Wang. Convergence and robustness of disturbance of direct time nonlinear systems with iterative learning control. Automatica 34 (1998) 1445- 1448 |
| [6] | J. X. Xu and Y. Tan. Robust optimal design and convergence properties analysis of iterative learning control approaches. Automatica 38 (2002) 1867- 1880 |
| [7] | H. S. Ahn. Intermittent iterative learning control. Proceeding of the IEEE 2006 international symposium on intelligent control. Munich, Germany, October 2006 |
| [8] | J. H. Moon. A robust approach for iterative learning control design for uncertain systems. Automatica 34 (2002) 1001- 1004 |
| [9] | H. Babaee, A. Khosravi. A Nonlinear ILC Schemes for Nonlinear Dynamic Systems To Improve Convergence Speed. IJCSI International Journal of Computer Science Issues, Vol. 9, Issue 3, No 1, May 2012 |
| [10] | A. Levant. Robust exact differentiation via sliding mode technique. Automatica, Vol 34, No 3, 379-384, 1998 |
| [11] | A. Levant. Universal SISO sliding mode controllers with finite time convergence. IEEE trans. Automat cntr. Vol 46, No 9. 1447-1451, 2001 |
| [12] | B. S. Yuri, I. A. Shkolnikov and A. Levant. Guide and control of missile interceptor using second order sliding mode. IEEE trans, Aero. Vol 45, No 1, 110-124, 2009 |
| [13] | Ramin Rajabioun. Cuckoo Optimization Algorithm. Applied Soft Computing 2011; 11: 5508–5518 |
| [14] | J. X. Xu. On iterative learning from different tracking tasks in the presence of time-varying uncertainties. IEEE Trans 34(2004) 589-597 |

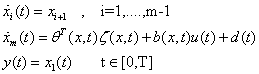
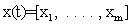 ,
, 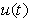 and
and 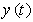 are the control input, respectively,
are the control input, respectively, 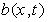 is unknown non-zero function,
is unknown non-zero function, 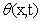 is a
is a 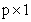 unknown and time varying function to be learnt,
unknown and time varying function to be learnt, 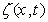 is known vector-valued function with dimension of
is known vector-valued function with dimension of 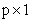 . The variable
. The variable 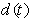 represent the unknown disturbance.Assumption 1: The desired output trajectory
represent the unknown disturbance.Assumption 1: The desired output trajectory 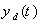 is differentiable with respect to time
is differentiable with respect to time 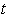 up to the mth order on a finite time interval[0, T], and all of the higher- order derivatives are available. Assumption 2: The unknown disturbance variable
up to the mth order on a finite time interval[0, T], and all of the higher- order derivatives are available. Assumption 2: The unknown disturbance variable 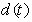 is bounded such that
is bounded such that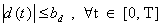 Where
Where 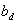 is a known constant.Assumption 3: The initial condition
is a known constant.Assumption 3: The initial condition 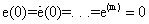 at any iteration
at any iteration 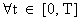 , such that the switching surface
, such that the switching surface 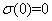 , where
, where 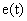 is the output tracking error that is defined as
is the output tracking error that is defined as 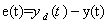 .The control objective is to design a continuous second-order sliding-mode iterative learning controller
.The control objective is to design a continuous second-order sliding-mode iterative learning controller 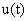 for the uncertain nonlinear system (1) such that system output can follow a desired one with a prescribed accuracy
for the uncertain nonlinear system (1) such that system output can follow a desired one with a prescribed accuracy 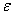 as follow:
as follow: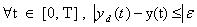
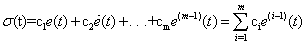
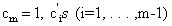 are coefficients of a Hurwitz polynomial, and
are coefficients of a Hurwitz polynomial, and 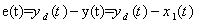 . Taking derivatives with respect to time
. Taking derivatives with respect to time 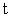 on both sides of (2), it is obtained:
on both sides of (2), it is obtained: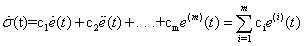
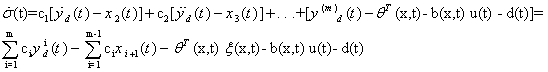
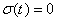 ,defines the system motion on the sliding surface. The control signal
,defines the system motion on the sliding surface. The control signal 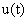 is to be designed as an iterative and continuous control input signal. The task of this work is to design such a continuous and iterative control input to steer the sliding surface in finite time interval.B. Robust ILC using Continuous Second-order Sliding ModeIn[10, 11], the second-order sliding-mode concept is originated. It is further developed in[12]. In reference to this work, the proposed continuous second-order sliding-mode ILC at kth iteration is designed as follow:
is to be designed as an iterative and continuous control input signal. The task of this work is to design such a continuous and iterative control input to steer the sliding surface in finite time interval.B. Robust ILC using Continuous Second-order Sliding ModeIn[10, 11], the second-order sliding-mode concept is originated. It is further developed in[12]. In reference to this work, the proposed continuous second-order sliding-mode ILC at kth iteration is designed as follow: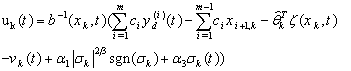
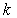 indicate the number of iteration,
indicate the number of iteration, 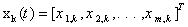 ,
,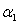 and
and 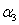 are positive constant.
are positive constant. 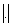 is the absolute value,
is the absolute value, 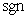 is the signum function,
is the signum function, 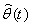 is the recursive control part that is used to learn the unknown function
is the recursive control part that is used to learn the unknown function 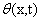 and generate by the following update law:
and generate by the following update law: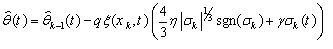
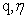 and
and 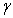 are positive constants.The variable
are positive constants.The variable 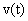 is an integral term that is defined below:
is an integral term that is defined below: 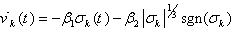
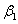 and
and 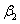 are positive constant.Controller (5), together with (6) and (7), defines the continuous second-order sliding-mode ILC.
are positive constant.Controller (5), together with (6) and (7), defines the continuous second-order sliding-mode ILC. 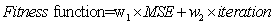
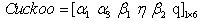
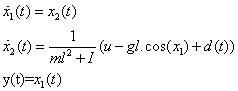
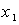 is the joint angle,
is the joint angle, 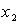 is the angular velocity,
is the angular velocity, 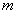 is the mass,
is the mass, 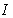 is the moment of inertia,
is the moment of inertia, 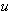 is the joint point and
is the joint point and 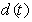 is a disturbance being
is a disturbance being 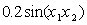 .Further the system output is
.Further the system output is 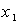 and the desired output trajectory is
and the desired output trajectory is 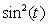 . The parameters take the values:
. The parameters take the values: 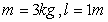 and
and 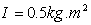 .Inserting the parameter values, (8) have an alternative form:
.Inserting the parameter values, (8) have an alternative form:
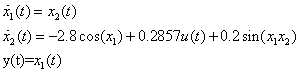
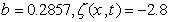 and
and 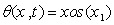 which is assumed unknown and to be learnt. Following (2), a switching surface is designed as:
which is assumed unknown and to be learnt. Following (2), a switching surface is designed as: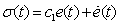
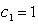 and
and 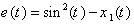 . Taking derivative on the above switching surface yields:
. Taking derivative on the above switching surface yields: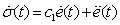
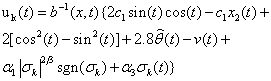






 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML

