1. Introduction

With the distributed delays the set of publications is devoted problems of identification of static plants. Such models are widely applied in econometrics and economy[1-4], to the technician[5-7], medicine[8-10]. Delay can have both independent, and dependent variables. The account of the distributed lags leads to autocorrelation between variables[1,2,4]. Autocorrelation hampers identification of parameters of plant. Various models of approximation of parameters are applied to a abatement of influence of autocorrelation on identification process at the distributed lags. It allows to reduce number of estimated parameters of plant. The Koyck scheme[2,12], based on a change of factors of model on a decreasing geometrical progression is most widely applied. The model I. Fisher[1,11] is based on a change of factors of model on the set decreasing arithmetical progression. Arithmetical and geometrical models are applied in that case when plant parameters decrease from the first members of a progression. Considering it, S. Almon[13] has added more flexibilities of model of I. Fisher, having applied polynomial the law of a modification of factors. In[11] the law of a change of factors is offered at the distributed lags according to logarithmic normal distribution. The same idea based on application the exponential law of distribution, is considered in[14]. In[15] Pascal distribution which leads to the simple form for factors is applied.

The a priori representation of correlation between the distributed lags in the form of some rational polynomial is considered in[16]. Other approaches to description of factors at the distributed lags are studied in[4].

The considered models of factors minimise number of unknown parameters. To an estimation of parameters apply a method least-squares method or its modifications[1-4]. In these works the model structure is postulated a priori and the problem of parametrical identification is considered. In[17] the interactive algorithm of an estimation of parameters of static plant with the distributed lags is offered. The length of a lag is set and does not become any suppositions about correlation between plant parameters. The case of a piecewise monotonic change of parameters of plant is considered. In a number of works methods of a choice of maximum length of a lag are offered. At the heart of applied approaches the statistics which are based on the analysis of residuals[1,15,18] lie. In[19, 20] various methods of an estimation of parameters of model with the distributed lag in a case of a priori set structure of model are considered. In[21] influence of the a priori information received from the analysis of the empirical data, on a choice of structure of model with the distributed lag on an output variable is analyzed. In work[22] are described algorithm of an estimation of parameters of model with the distributed lag. On the basis of results of modelling the structure of model which explains a mismatch of model applied now in the American interest rate on federal funds is selected. In[23] process of inflation with the help autoregressive models is researched. The choice of length of a lag is carried out on the basis of consecutive magnification of delays and an estimation of adequacy of the received model. Then the criterion of Akaike and Bayesian Information Criteria are applied and the solution is made on model structure. The case of a priori uncertainty concerning structure and plant parameters was not study.

In the given work the approach to structural identification of static plants in the conditions of uncertainty is offered. It is based on application of the static structures describing properties of plant[24] in special space. The criterion of linearity (autocorrelation) of variables of plant is introduced. Algorithms of decision-making on maximum length of the distributed lag are offered. They do not demand an evaluation of the statistics. The analogue of criterion Darbina-Watson criterion for a considered case is reduced.

2. Problem Statement

Consider plant

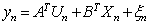(1)

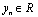where is an exit, 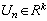is the input vector which elements are limited, is limiting nondegenerate functions, 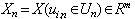is a vector of the distributed lags on 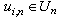, , 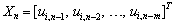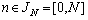is discrete time,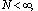 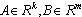are vectors of constant parameters, 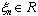is a perturbation, 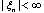for all .

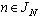Consider that general case 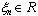and 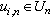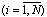are irregular functions of time.

For (1) the set of the measured values is known

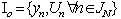(2)

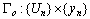
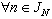and map describing an observable informational portrait[7,24].

It is necessary 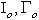to estimate on the basis of analysis structure of plant (1). It means that it is necessary to estimate degree of linearity and dimension of vector .

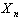3. An Estimation of Level of Linearity of System (1)

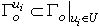
Consider a contraction of observable informational portrait 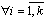and for everyone construct a secant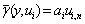

where 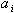are some real numbers.

Introduce set on (2) set of secants for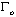

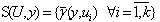Definition 1[24]. Field of structures 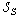of system (1) name set of maps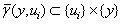 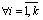on Euclidean plane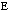

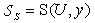Designate 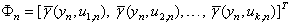and consider the equation

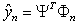(3)

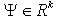where vector define by means of a least-squares method. Estimation exists on the basis of the suppositions made in section 2 concerning input .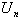

Completeness of system (1) in the field of structures 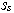estimate on the basis of the following statement[24].

Theorem 1. Consider a vector of informative variables 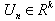and a field of structures 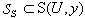for (1). Then the field of structures 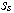of system (1) is full, if

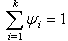(4)

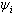where there is 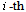element of vector 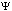in (4).

The theorem 1 gives linearity sufficient conditions (nonlinearities, collinearity) systems (1) on the set field of structures 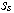. If the condition (4) is fulfilled, that field 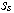is full. Hence 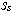is a linear span of an exit of system (1). Otherwise make a solution on presence of nonlinearity or collinearity (autocorrelation) in system (1).

Let

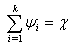Magnitude 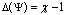name level of nonlinearity of system (1) in parametrical space 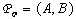. As nonlinearities and lags lead to occurrence multicollinearity in (1) 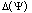will accept small values.

4. Set for an Estimation of Structure of the Distributed Lag of Plant

Following[7,24], generate auxiliary set for an estimation of structure (1). Introduce variable 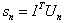, where 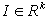is an unit vector, and apply model 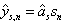. Define parameter 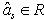from a condition

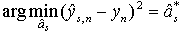(5)

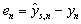Let is a variable which contains the data about structure of a lag of system (1). As argument 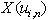use variable 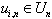which ensures maximum value of coefficient of determination 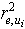between and 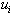. As shown in[24], set 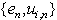does not allow to solve a problem of structural identification. Therefore introduce coefficient of structural properties (CSP)[7]

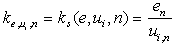(6)

and generate set

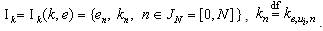Definition 2. Name 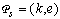structural space of the system (1), allowing to identify structure of vector .

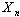On 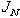will order 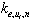on increase. Generate 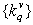, where 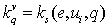, 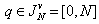. As to everyone 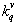there corresponds value 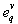receive 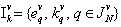. In 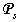define map 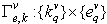and structure 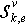corresponding to it. Now the problem is shown to an estimation of structure 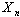on the basis of analysis 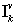and 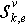. Such approach well works at an estimation of structure of nonlinear static systems[24]. For systems with the distributed lag he demands modification.

5. Decision-Making on Length of a Lag in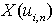

Set 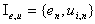contains uncertainty 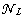and 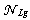. 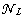is an incomplete account of linear making system (1). 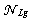is a presence of perturbation from the distributed lag. For elimination 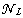construct a secant for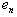

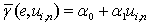where 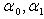define as a solution of a problem (5).

Introduce new variable 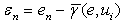which does not contain 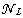. For estimation 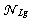analyse set .

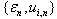For deriving of a provisional estimate of maximum lag fulfil following operations. Set admissible level 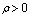of coefficient of determination 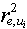. Apply the following algorithm.

Algorithm .

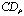1. Suppose .

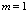2. Construct a secant

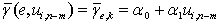and define .

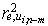3. Verify up condition .

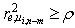4. If the condition is fulfilled, suppose 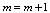and go to a step 2, differently finish work.

In work the multiple-functional approach to structural identification is applied. Therefore known methods of a choice of length of the lag, based on statistical criteria (section 1 see), are inapplicable.

Considering it, to an estimation of independence of elements of vector 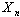apply the theorem 1. As the analysis of set 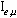is in this case ineffective, that use results of section 4 and generate set

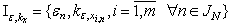(7)

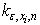where calculate on the basis of (6), considering , .

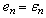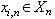On 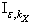will introduce transformation

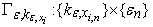to which in space 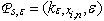there corresponds structure 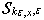, 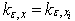. Construct secants for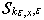

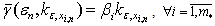(8)

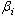where are the coefficients defined as a result of a solution of a problem (5), 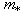is value m received on the basis of application of algorithm .

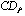Generate a vector

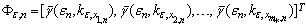(9)

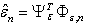and apply model to forecasting of change 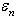, where vector 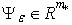is defined on the basis of outcomes of section 3.

The statement following directly from the theorem 1 is fair.

Theorem 2. Let on set 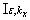the field of secants for 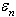is constructed

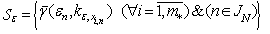and model 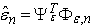is applied to forecasting of a change of variable 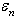. Then vector is an element of structure of system (1), if

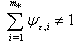where 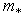it is defined by means of algorithm , .

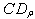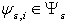Remark. As 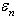contains the information on influence of vector 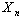at statistical interpretation 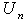, 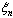use analag of criterion of criterion of Darbin-Watson

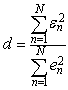Level of nonlinearity of the system (1), generated by correlation of elements of vector 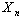is equal

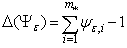Theorem 3. Consider the set of secants 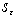set on 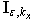and secant 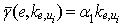for 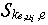. Let for them coefficients of determination 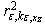, 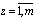and 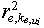are known. Then vector 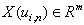is an element of structure of system (1), if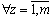

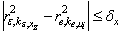where 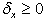is a specified magnitude.

At structure 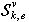analysis, the distributed lag of system (1) interpret as a nonlinear component (1). Therefore design the corresponding procedure, allowing to make the solution on a class of uncertainty 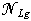. Apply the following approach.

Consider set 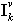and static structure 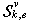corresponding to it. Construct the secants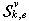

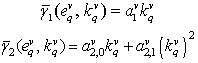and define for them coefficients of determination , .

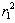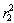Consider CSP

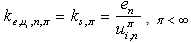(10)

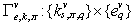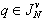and map , to which there corresponds structure 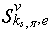. Construct for 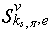a secant

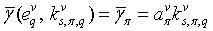(11)

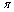and parameter select so that the factor of determination 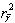for (11) belonged to interval .

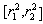Further consider CSP

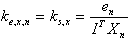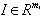where is an unit vector. Construct a secant for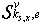

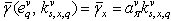(12)

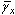Designate coefficient of determination for through .

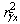Theorem 4. Consider structures 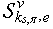, 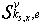and secants (11), (12) corresponding to them. If for structure 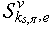, 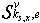secants the condition is satisfied

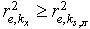then 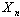is an element of structure of system (1).

The proof of the theorem 4 is obvious. It is based that structures 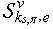, 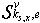describe a change of same variable 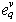. Therefore a solution about inclusion in structure of system (1) accept concerning that variable 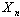, 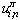which ensures greater coefficient of determination.

Statement. If coefficient of determination 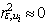, then .

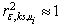Proof. From 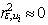follows that parameter 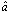of model 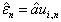predicting a change of variable 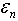, is equal to zero. Then for 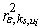receive

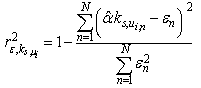(13)

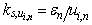where . Substituting 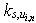in (13), for fraction numerator receive

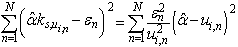(14)

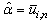If where there is average value 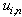, then.

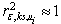Results of modelling confirm the made statement.

Consider a case when vector 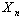in (1) contains the distributed lags on 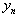, that is .

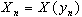6. Decision-Making on Length of a Lag for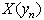

Let 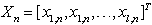, where 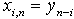, 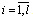. To tentative estimation 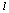apply algorithm 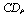. Decision-making in space 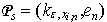, can appear ineffective because of connections between 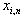. Therefore consider space 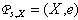set on set 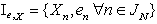. Consider structure 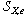and its projections 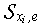to plane 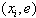. For everyone 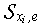define secants 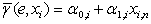, 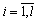Also generate a vector

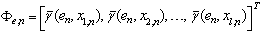(15)

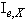Theorem 5. Let on set the field of secants for 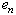is constructed

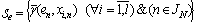and model 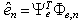is applied to forecasting of variable 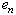. Then vector 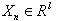is an element of structure of system (1), if

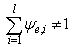(16)

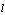where define by means of algorithm , .

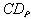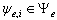The theorem 5 is analogue of the theorem 2. Performance (16) specifies on presence of dependence between 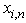. At statistical interpretation of a problem (16) speaks about autocorrelation of residuals[1]. Level of nonlinearity of system (1) estimate by means of .

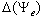For an estimation of existence of a lag on 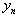analyse a change CSP

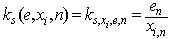As the log on 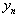is considered, then

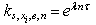(17)

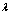where is an eigenvalue of system (1) with 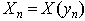, is an interval of measurement of the data.

The problem consists in estimation 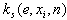on the basis of analysis 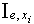and identification of parameter 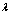on set 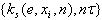. To estimation 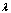apply Lyapunov characteristic indicators.

Apply model 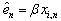to forecasting of change 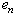and define parameter 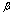by means of a least-squares method. To description 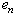also apply model 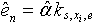, where 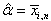. From comparison of these two models receive

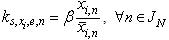(18)

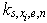Arrange values in ascending order and receive set 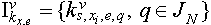. Define for 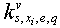of Lyapunov characteristic indicator[25]

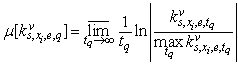(19)

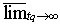where is an limit superior, .

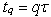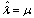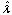Suppose where there is estimation 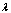. To an improving of received estimation 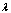apply the approach offered in[24].

Remark. Estimation 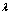serves as the indicator of presence at system (1) distributed lags on 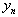. Exact estimation 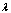define only at a step of parametrical identification.

Consider the more general case when vector 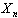in (1) is equal 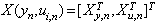, where , .

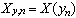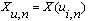7. Decision-Making on Length of a Lag for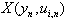

Spread the approach stated above to system (1) with 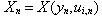. The provisional estimate of level of linearity of system (1) receive by means of the theorem 1. Introduce variable 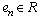which depends on uncertainty 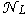. Apply algorithm 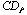to definition of dimension of vectors 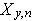, 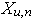. For elimination of influence 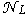construct a secant for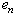

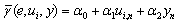where define as a solution of a problem (5).

Introduce new variable 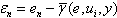which does not contain 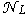. To decision-making on lag presence apply results of sections 5, 6.

8. Examples

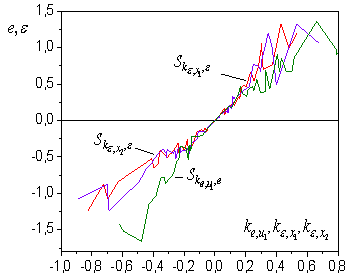Figure 1. Structures for decision-making on length of lag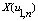

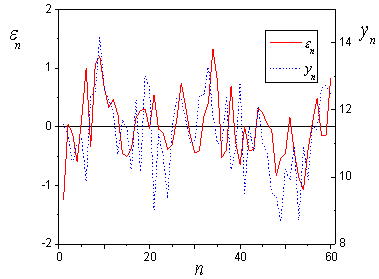Figure 2. Variables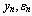

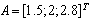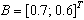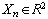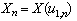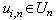Consider system (1) with , , , . are limited random functions, 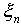is an stochastic variable with zero expectation and a final variance, 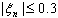. Application of the theorem 1 has shown that the system is not linear, 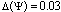. Receive set

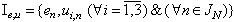Analysis has shown that variable has a lag. Apply algorithm 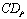and the theorem 2. The length of a lag on 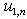is equal 2. Indicator 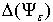practically coincides with 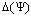. To an correction of the received estimation of length of a lag apply the theorem 3 with 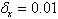. 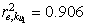, , 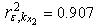, 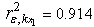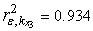. Corresponding structures on which the theorem 3 is based, are shown on fig. 1. Corresponding structures on which the theorem 3 is based, are shown on fig. 1.

On fig. 2 show variables 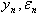. They confirm presence at system of the distributed lag on 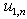. As inputs are random calculate criterion 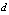. Receive 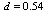that following[2], confirms result about presence a lag.

Consider system (1) with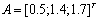 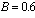, 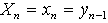. Receive indicator 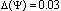. Make a solution on presence multicollinearity (nonlinearity) in systems. Apply algorithm 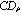. Receive 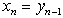. The length of a lag is equal 1. Generate variable 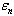on the basis of a method described in section 5. On fig. 3 show variables 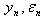to estimate delay presence on .

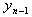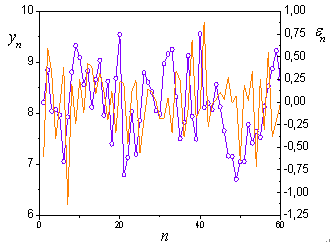Figure 3. Delay in system (1) with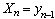

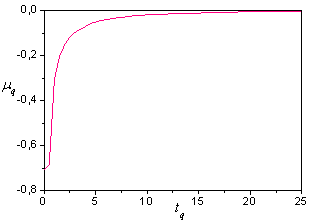Figure 4. Lyapunov characteristic index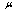

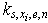For validation of the received conclusion estimate CSP at 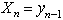, using dependences (17), (18) and (19). Problem reduce to estimation 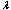in (17). On fig. 4 show change 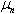on the basis of (19). Suppose 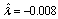. More exact estimation 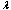in (17) define, using a method offered in[24]. Receive .

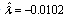9. Conclusions

The is functional-multiple approach to structural identification of static systems with the distributed lag is offered. Solution about structure of the distributed lag of system receive on the basis of the analysis of special static structures. The criterion of an estimation of degree of linearity of system in parametrical space is introduced. It is considered variants of identification of system in the availability of a lag on dependent and independent variables. The approach to an