-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2012; 2(5): 127-135
doi: 10.5923/j.control.20120205.05
Structural Observability of Controlled Switching Linear Systems
Hicham Hihi
Electrical Engineering Department, LGECOS, Cadi Ayyad University, ENSA, Av Abdelkrim khattabi BP, 57540000, Marrakech, Morocco
Correspondence to: Hicham Hihi , Electrical Engineering Department, LGECOS, Cadi Ayyad University, ENSA, Av Abdelkrim khattabi BP, 57540000, Marrakech, Morocco.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, a new methodology for analysis of structural observability of controlled switching linear systems modelled by bond graphs is proposed. Causal manipulations on the bond graph model enable to determine graphically the observable subspace. A novel definition of observability is proposed. Finally, two sufficient conditions of observability are derived. The proposed method, based on a bond graph theoretic approach, assumes only the knowledge of the systems structure. These conditions can be implemented by classical bond graph theory algorithms based on finding particular paths and cycles in a bond graph.
Keywords: Hybrid Systems, Switching Systems, Bond Graph, Structural Observability
Cite this paper: Hicham Hihi , "Structural Observability of Controlled Switching Linear Systems", International Journal of Control Science and Engineering, Vol. 2 No. 5, 2012, pp. 127-135. doi: 10.5923/j.control.20120205.05.
Article Outline
1. Introduction
- Hybrid dynamic systems constitute a particular class of dynamic systems in which some elements (called switching components) or phenomena evolve much faster than the time scale at which the system behaviour needs to be analysed[16]. Such systems, also called switched systems, are widespread in physical and engineering fields (hydraulic systems with valves, electrical systems containing diodes, relays or transistors,…, mechanical systems with clutches or collisions...). In this present work, I investigate the observability issue for controlled switching linear systems modelled by bond graph. My obtained results present a graphical method based on an energy concept.Observability is a fundamental concept in modern control theory of systems, has been extensively studied both in the continuous and in discrete domains. More recently various researchers have approached the study of observability for hybrid systems[2, 14, 15, 18, 19]. Ezzine and Haddad[12] first studied the one-period controllability and observability for periodically switched systems, some sufficient and necessary conditions were established. Then, Xie and Zheng[6] introduced the multiple-period controllability and observability concepts naturally extended from the one-period ones, necessary, and sufficient criteria were derived. It was also pointed out that controllability can be realized in n periods at most, where n is the state dimension. As to arbitrarily switched linear systems, Sun and Zheng[21] first gave a sufficient condition and a necessary condition for controllability and proved that the necessary condition is also sufficient for three-dimensional systems with only two subsystems. Following the work in[21] and[22] extended the result to three-dimensional systems with arbitrary number of subsystems. Then, necessary and sufficient geometric type criteria for controllability and observability were derived in[22] and[7]. Vidal and al.[18] considered autonomous switching systems and proposed a definition of observability based on the concept of indistinguishability of continuous initial states and discrete state evolutions from the outputs in free evolution. Incremental observability was introduced in[2] for the Class of Piecewise Affine (PWA) systems. Incremental observability implies that different initial states always give different outputs independently of the applied input. In[1], a methodology was presented for the design of dynamic observers of hybrid systems that reconstructs the discrete state and the continuous state from the knowledge of the continuous and discrete outputs. In[10], the definitions of observability of[19] and the results of[1] on the design of an observer for deterministic hybrid systems are extended to discrete-time stochastic linear autonomous hybrid systems.In order to obtain a more realistic model for the analysis of system properties, the concept of structural property has been introduced in[5], is true for almost all values of the parameters. This framework is consistent with physical reality in the sense that system parameter values are never exactly known, with an exception for zero values that express the absence of interactions or connections. The elements of a structural matrix[A] are either fixed at zero or indeterminate values that are assumed to be independent of one another. Hence it is desirable to investigate system properties that are only determined by the structure of the system and not by the parameter numerical values. A useful tool for this purpose is the bond graph approach, which has received a great deal of attention in the last decade[5, 17]. This approach has been used for the analysis of structural properties of linear systems[3, 4, 9].This paper is organized as follows: The second section, formulates the Controlled Switching Linear Systems (CSLS) observability. Section three recalls some background about bond graph modelling of hybrid systems with ideal switches. In section four the structural observability of these systems is discussed using bond graph model. Graphical conditions and procedures are also proposed. Finally, a simple example which illustrates the previous results is discussed.
2. Observability of Controlled Switching Linear Systems
- Consider a controlled switching linear systems[23], described by
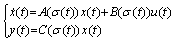 | (1) |
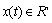 is the state variable,
is the state variable, 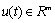 is the input variable, and
is the input variable, and 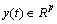 is the output variable.
is the output variable. 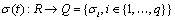 is a piecewise constant switching function and
is a piecewise constant switching function and 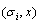 the hybrid state.If we consider this system in a particular mode i, the equation (1) can be written as :
the hybrid state.If we consider this system in a particular mode i, the equation (1) can be written as : | (2) |
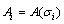 ,
, 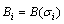 ,
, 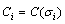 ,
,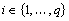 and q the number of mode.Remark 1 System (2) can be considered as a linear time invariant system (LTI).Assumptions 11) We suppose that
and q the number of mode.Remark 1 System (2) can be considered as a linear time invariant system (LTI).Assumptions 11) We suppose that 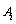 ,
, 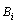 and
and 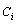 matrices are constant on
matrices are constant on 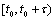 ,where
,where 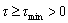 , and constant
, and constant 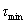 is an arbitrarily small and independent of mode
is an arbitrarily small and independent of mode 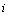 . For instance, suppose that the dynamics in (1) are given by
. For instance, suppose that the dynamics in (1) are given by 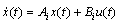 over the finite time interval
over the finite time interval 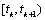 . At time
. At time 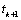 the dynamic in interval
the dynamic in interval 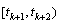 is given by
is given by 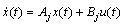 . 2) We assume that the state vector
. 2) We assume that the state vector 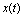 does not jump discontinuously at
does not jump discontinuously at 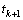 .Under these assumptions, the observability of (1) was defined:Definition 1[22] The CSLS (1) is observable, if there exist a time
.Under these assumptions, the observability of (1) was defined:Definition 1[22] The CSLS (1) is observable, if there exist a time 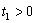 and a switching path
and a switching path 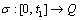 , such that initial state
, such that initial state 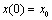 can be determined by the corresponding system input
can be determined by the corresponding system input 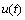 and the system output
and the system output 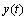 ,
, 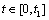 .
.2.1. An Algebraic Sufficient Condition
- In order to investigate observability of (1), the following zero input system is considered.
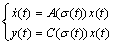 | (3) |
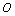 [9] of system (1) is given by equation (4),
[9] of system (1) is given by equation (4),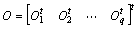 | (4) |
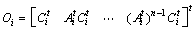 is the observability matrix of the
is the observability matrix of the 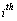 mode.Theorem 1[9] The CSLS (1) is observable, if
mode.Theorem 1[9] The CSLS (1) is observable, if 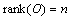 .Remark 2 From this theorem, we can deduce that:1) The system (1) can be observable, if there is only one observable sub-system (mode). 2) However, it is possible that no sub-system is observable but that the system (1) is observable.
.Remark 2 From this theorem, we can deduce that:1) The system (1) can be observable, if there is only one observable sub-system (mode). 2) However, it is possible that no sub-system is observable but that the system (1) is observable.2.2. A necessary and Sufficient Algebraic Condition
- References[9] and[22] define the subspace sequence
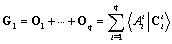 ,
, 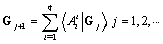 and
and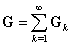 | (5) |
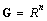 .This theorem is a geometric criterion, thus, it is easy to transform it into algebraic form.Definition 2The joint observability matrix of system (1) is defined as :
.This theorem is a geometric criterion, thus, it is easy to transform it into algebraic form.Definition 2The joint observability matrix of system (1) is defined as :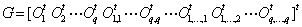 | (6) |
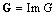 .Theorem 3[9]System (1) is observable, if and only if
.Theorem 3[9]System (1) is observable, if and only if 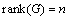 .Proof.For
.Proof.For 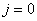 , we have :
, we have :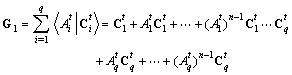
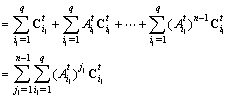 For
For 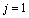 , we have :
, we have :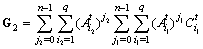 In a similar way one finds :
In a similar way one finds :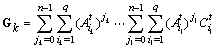 However
However 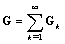 and
and 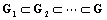 , then
, then 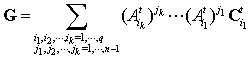 Of another share, we have :
Of another share, we have :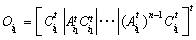
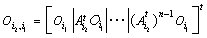

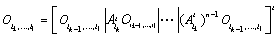 With
With 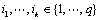 ,
, 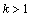 ,and
,and 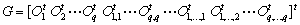 Then
Then 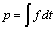 .We exposed algebraic and geometric criteria of analysis of the properties of observability of CSLS. The next section is devoted to the graphic interpretation of these results by using the Bond graph approach.
.We exposed algebraic and geometric criteria of analysis of the properties of observability of CSLS. The next section is devoted to the graphic interpretation of these results by using the Bond graph approach.3. Bond Graph Approach
- The bond graph structure junction contains informations on the type of the elements constituting the system, and how they are interconnected, whatever the numerical values of parameters. The structure junction of a switching bond graph can be represented by Figure 1. Five fields model the components behaviour, four fields that belong to the standard bond graph formalism; - source field which produces energy, - detector field; - R field which dissipates it, - I and C field which can store it, - and the Sw field that is added for switching components. Figure 1 represents the block diagram that is deduced from the causal bond graph.The following key variables are used :- the state vector x(t)is composed of the energy variables on the bond connected to an element in integral causality (the momenta
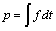 on I elements and charges
on I elements and charges 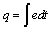 on C elements), and the complementary state vector z(t)is composed of power variables (the efforts eon Celements and flows f on I elements); -
on C elements), and the complementary state vector z(t)is composed of power variables (the efforts eon Celements and flows f on I elements); - 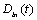 and
and 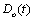 represent the variables going out of and into the R field; - the vector u(t)is composed of the sources; -
represent the variables going out of and into the R field; - the vector u(t)is composed of the sources; - 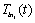 is composed of the zero valued variables imposed by the switches in this configuration; -
is composed of the zero valued variables imposed by the switches in this configuration; - 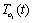 is composed of the complementary variables in the switches; - the vector y(t) is composed of the continuous outputs.
is composed of the complementary variables in the switches; - the vector y(t) is composed of the continuous outputs.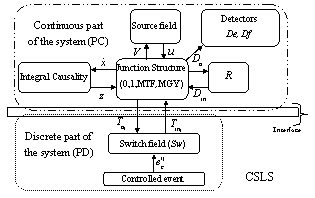 | Figure 1. Structure junction |
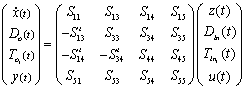 | (7) |
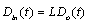 .
. 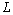 is a positive matrix. Let assume that
is a positive matrix. Let assume that 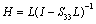 is an invertible positive matrix. Then the second row leads to
is an invertible positive matrix. Then the second row leads to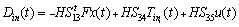 .The third line of (7) gives :
.The third line of (7) gives :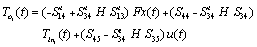 | (8) |
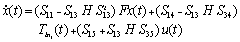 | (9) |
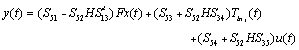 | (10) |
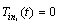 .
.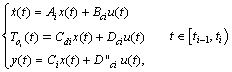 | (11) |
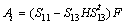 ,
, 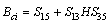 ,
, 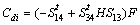 ,
, 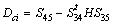 ,
, 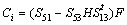 and
and 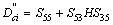 .Therefore, for N switches and by considering
.Therefore, for N switches and by considering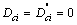 , we have
, we have 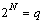 modes :
modes :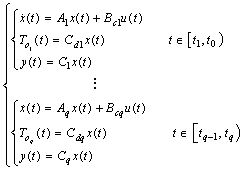 | (12) |
4. Structural Observability
- The bond graph concept is an alternate representation of physical systems. Some recent works permit to highlight structural properties of these systems[4]and[3]. In[4], the structural observability property is studied using simple causal manipulations on the bond graph model. It is shown that the structural rank concept is somewhat different for bond graph models because it is more precise than for other representations. Our objective is to extend these properties to CSLS systems. In the following we note that:-BG: acausal (without causality) bond graph model,-BGI: bond graph model when the preferential integral causality is affected,-BGD: bond graph model when the preferential derivative causality is affected,-
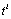 : the number of elements in integral causality in BGDi. i indicate the mode i.-
: the number of elements in integral causality in BGDi. i indicate the mode i.- 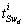 : the number of elements remaining in integral causality in BGDi, when a dualization of the maximum number of continuous output y and discrete output
: the number of elements remaining in integral causality in BGDi, when a dualization of the maximum number of continuous output y and discrete output 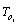 is applied (in order to eliminate elements in integral causalities).To study structural observability of CSLS modelled by bond graph, graphical methods are proposed in the form of two sufficient conditions. In fact, formal representation of observability subspace is given for bond graph models. It is calculated through causal manipulations. The base of this subspace is used to propose a procedure to study the system observability.
is applied (in order to eliminate elements in integral causalities).To study structural observability of CSLS modelled by bond graph, graphical methods are proposed in the form of two sufficient conditions. In fact, formal representation of observability subspace is given for bond graph models. It is calculated through causal manipulations. The base of this subspace is used to propose a procedure to study the system observability.4.1. Graphical Sufficient Condition 1
- A system (1) with q modes is observable if only one system (2) is observable. This condition can be interpreted by using the result of structural observability of LTI system. Indeed, this result is a simple recovery of those giving the necessary and sufficient condition of structural observability of LTI system modelled by bond graph approach[4].Theorem 4 The CSLS system is structurally state observable if:- On the BGIi, all dynamical elements in integral causality are causally connected with a continuous output De or Df associated to y(t) or a discrete output Sw associated to
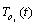 .- BG-rank
.- BG-rank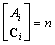 . With
. With 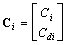 ,
, 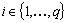 .Property 1 BG-rank
.Property 1 BG-rank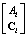 =rank
=rank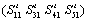
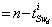 .Example 1 We consider the following acausal bond graph model. Shown in Figure 2:
.Example 1 We consider the following acausal bond graph model. Shown in Figure 2:  | Figure 2. Acausal bond graph model |
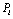 on
on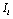 ,
, 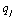 on
on 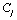 (
( ). The dimension of the system is
). The dimension of the system is 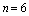 . We have one switch, then the number of possible configurations is
. We have one switch, then the number of possible configurations is 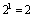 . The bond graph models in integral causality for these two configurations (modes) are given by Figure 3.
. The bond graph models in integral causality for these two configurations (modes) are given by Figure 3.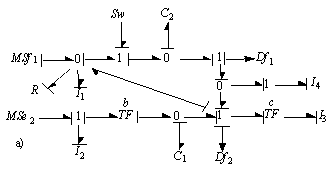 | Figure 3a. Bond graph model in integral causality (mode 1) :  : : |
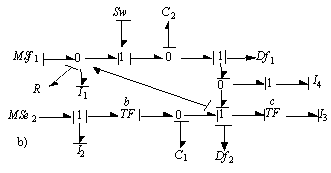 | Figure 3b. Bond graph model in integral causality (mode 2) :  : :  |
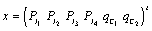 .The application of the derivative causality, for example on mode 1 (Figure 3.a), give the following BGD1 (Figure 4).
.The application of the derivative causality, for example on mode 1 (Figure 3.a), give the following BGD1 (Figure 4).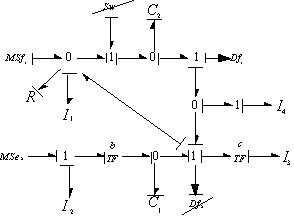 | Figure 4. BGD1 + dualization of detectors |
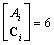 , this mode is observable by continuous outputs Df1 and Df2 and discrete output
, this mode is observable by continuous outputs Df1 and Df2 and discrete output 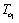 , then the system is structurally observable. This result can be verified using formal calculation on the bond graph model in integral causality[3].To study the observability of system (12), it is necessary to apply this result to all modes; if one observable mode exists, the procedure is stopped. The case where no mode is observable, but when the system is observable, can be verified by formal calculation of combined matrix (4). This calculation can be formally effected :- by using the bond graph model in integral causality[3], or - by calculating the observability subspace from bond graph model in derivative causality.We chose to translate the latter in the form of a second sufficient condition. For that, formal representation of structural observability subspace, denoted as
, then the system is structurally observable. This result can be verified using formal calculation on the bond graph model in integral causality[3].To study the observability of system (12), it is necessary to apply this result to all modes; if one observable mode exists, the procedure is stopped. The case where no mode is observable, but when the system is observable, can be verified by formal calculation of combined matrix (4). This calculation can be formally effected :- by using the bond graph model in integral causality[3], or - by calculating the observability subspace from bond graph model in derivative causality.We chose to translate the latter in the form of a second sufficient condition. For that, formal representation of structural observability subspace, denoted as 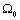 , is given for BG model. It is calculated using causal manipulations. The base of this subspace is used to propose a procedure to study the structural observability of system.
, is given for BG model. It is calculated using causal manipulations. The base of this subspace is used to propose a procedure to study the structural observability of system. 4.2. Graphical Sufficient Condition 2
- On the BGDi (and dualization of continuous and discrete outputs) there exists
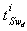 elements remaining in integral causality and
elements remaining in integral causality and 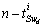 elements in derivative causality.
elements in derivative causality.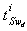 algebraic equations can be written (Equation (13)) :
algebraic equations can be written (Equation (13)) :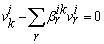 | (13) |
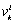 is either an effort variable
is either an effort variable 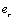 for
for 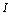 -element in integral causality or a flow variable
-element in integral causality or a flow variable 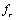 for
for 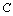 -element in integral causality,-
-element in integral causality,-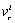 is either an effort variable
is either an effort variable 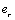 for
for 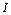 -element in derivative causality or a flow variable
-element in derivative causality or a flow variable 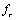 for
for 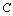 - element in derivative causality,-
- element in derivative causality,-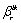 is the gain of the causal path between the
is the gain of the causal path between the 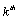
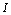 or
or 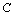 -elements in integral causality and the
-elements in integral causality and the 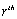
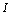 or
or 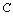 -elements in derivative causality.Let us consider the
-elements in derivative causality.Let us consider the 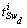 column vectors
column vectors 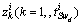 whose components are the coefficients of the variables
whose components are the coefficients of the variables 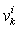 and
and 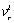 in equation (13).Property 2The
in equation (13).Property 2The 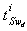 column vectors
column vectors 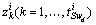 are orthogonal to the structural observability subspace vectors of the
are orthogonal to the structural observability subspace vectors of the 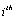 mode. We write
mode. We write 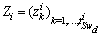 and
and 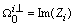 .Procedure 1Calculation of
.Procedure 1Calculation of 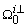 1) On the BGDi, dualize the maximum number of output detectors in order to eliminate the elements in integral causality,2) For each element in integral causality, write the algebraic relations with elements in derivative causality (equation 13),3) Write a column vector
1) On the BGDi, dualize the maximum number of output detectors in order to eliminate the elements in integral causality,2) For each element in integral causality, write the algebraic relations with elements in derivative causality (equation 13),3) Write a column vector 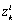 for each algebraic relation with the causal path gains (Equation (13)).
for each algebraic relation with the causal path gains (Equation (13)).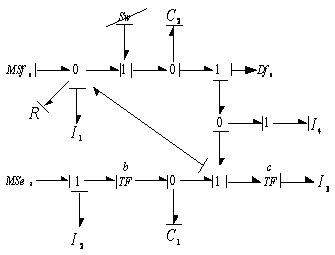 | Figure 5a. Bond graph model in derivative causality (mode 1) |
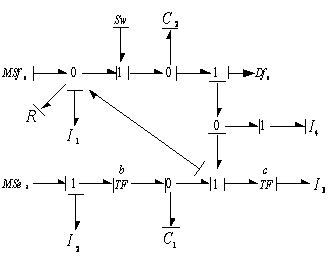 | Figure 5b. Bond graph model in derivative causality (mode 2) |
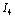 is in integral causality, so wecan write
is in integral causality, so wecan write 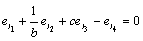 . The coefficients of the algebraic relation are multiplied by the inductance or capacitance parameter, because of the form of the output matrix in the state equation. Thus we obtain
. The coefficients of the algebraic relation are multiplied by the inductance or capacitance parameter, because of the form of the output matrix in the state equation. Thus we obtain 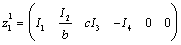 .In order to calculate a
.In order to calculate a  basis,it is enough to find
basis,it is enough to find  independent row vectors
independent row vectors 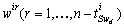 . These vectors are gathered in the matrix given by
. These vectors are gathered in the matrix given by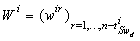 .In the same manner, from the BGDi (and dualization of output detectors)
.In the same manner, from the BGDi (and dualization of output detectors) 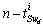 algebraic relations can be written (14).
algebraic relations can be written (14).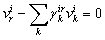 | (14) |
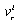 is either a flow variable
is either a flow variable 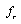 for
for 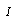 -element in derivative causality or an effort variable
-element in derivative causality or an effort variable 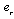 for
for  - element in derivative causality,-
- element in derivative causality,- 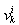 is either a flow variable
is either a flow variable 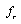 for
for 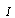 -element in integral causality or a flow variable
-element in integral causality or a flow variable 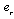 for
for  - element in integral causality,-
- element in integral causality,- 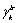 is the gain of the causal path between the
is the gain of the causal path between the 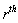 element in derivative causality and the
element in derivative causality and the 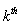 element in integral causality. Suppose now the
element in integral causality. Suppose now the 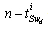 row vectors
row vectors 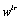 whose components are the coefficients of the variables
whose components are the coefficients of the variables 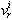 and
and 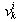 in equation (14).Procedure 2 Calculation of
in equation (14).Procedure 2 Calculation of 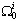 1) On the BGDi, dualize the maximum number of output detectors in order to eliminate the elements in integral causality.2) For each element remaining in derivative causality, write the algebraic relation with elements in integral causality, (Equation (14)).3) Write a row vector
1) On the BGDi, dualize the maximum number of output detectors in order to eliminate the elements in integral causality.2) For each element remaining in derivative causality, write the algebraic relation with elements in integral causality, (Equation (14)).3) Write a row vector 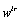 for each algebraic relation with the different gains of the causal paths, (Equation (14)).Property 3The
for each algebraic relation with the different gains of the causal paths, (Equation (14)).Property 3The 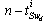 row vectors
row vectors 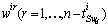 compose a basis for the structural observability subspace of
compose a basis for the structural observability subspace of 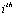 mode.With
mode.With 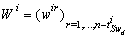 and
and 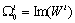 .Example 3 We implement procedure 2on the previous example. For mode 1, the two dynamic elements
.Example 3 We implement procedure 2on the previous example. For mode 1, the two dynamic elements 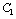 and
and 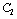 are not causally connected with
are not causally connected with 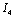 , we can write
, we can write 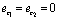 , the corresponding vectors are
, the corresponding vectors are 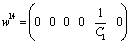 and
and 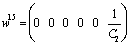 . The algebraic equations corresponding to the elements
. The algebraic equations corresponding to the elements 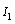 ,
, 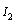 and
and 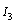 are given by :
are given by : 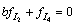
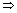
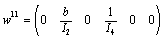 ,
, 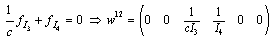 and
and 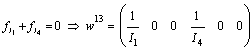 . Thus, we have
. Thus, we have 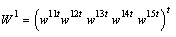 and
and 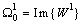 .Some calculation is carried out for mode 2. We obtain
.Some calculation is carried out for mode 2. We obtain 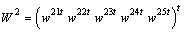 , with
, with 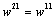 ,
, 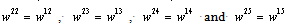 a, and
a, and 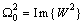 .The graphical calculation of structural observability subspaces and remark 2 lead to theorem 5.Theorem 5 If
.The graphical calculation of structural observability subspaces and remark 2 lead to theorem 5.Theorem 5 If 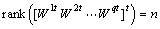 , the CSLS system is structurally observable.Proof. We have shown for a given mode that the bond graph model in derivative causality is characterized by an algebraic equation of the form (14) from which, we construct a
, the CSLS system is structurally observable.Proof. We have shown for a given mode that the bond graph model in derivative causality is characterized by an algebraic equation of the form (14) from which, we construct a 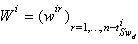 base of structural observability subspace of the ith mode, denoted
base of structural observability subspace of the ith mode, denoted 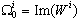 .After commutation from ith mode to (i+1)th mode, implement a derivative causality on the bond graph model and dualization the maximum number of continuous and discrete outputs. We can write another algebraic relation (equation 15).
.After commutation from ith mode to (i+1)th mode, implement a derivative causality on the bond graph model and dualization the maximum number of continuous and discrete outputs. We can write another algebraic relation (equation 15).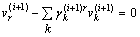 | (15) |
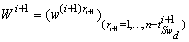 .However, the condition :
.However, the condition : 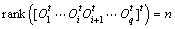 is sufficient for observability of the system, which implies that condition
is sufficient for observability of the system, which implies that condition 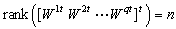 is also sufficient.Example 4 Theorem 5 is now applied to the previous bond graph model, we have
is also sufficient.Example 4 Theorem 5 is now applied to the previous bond graph model, we have 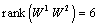 , then, this system is structurally controllable.
, then, this system is structurally controllable.5. Example
- Let us consider the following acausal BG model (figure 6).
 | Figure 6. The acausal BG |
 | Figure 7. The BGIi, a) mode 1, b) mode 2, c) mode 3, d) mode 4 |
 | Figure 8. BGDi + dualization of detectors |
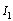 and
and 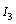 stays in integral causality. After dualization of the discrete output
stays in integral causality. After dualization of the discrete output 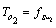 associated to
associated to 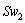 , only one element
, only one element 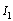 remaining in integral causality (figure 8.A), So this mode is not observable.In the same way, the other modes are not observable, therefore, step 1 is not verified.Step 2 : Verification of sufficient condition 2▪ Calculation of W1 (mode 1)For mode 1, the element
remaining in integral causality (figure 8.A), So this mode is not observable.In the same way, the other modes are not observable, therefore, step 1 is not verified.Step 2 : Verification of sufficient condition 2▪ Calculation of W1 (mode 1)For mode 1, the element 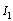 is in integral causality, we have one algebraic relation can be written
is in integral causality, we have one algebraic relation can be written 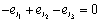 . The coefficients of the algebraic relation are multiplied by the inductance or capacitance parameter, because of the form of the output matrix in the state equation. Then
. The coefficients of the algebraic relation are multiplied by the inductance or capacitance parameter, because of the form of the output matrix in the state equation. Then 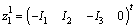 .The algebraic equations corresponding to the elements
.The algebraic equations corresponding to the elements  and
and  are given by:
are given by: 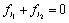 ,
, 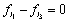 , then
, then 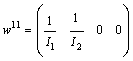 ,
, 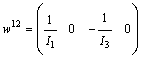 . The dynamical element C is not causally connected with
. The dynamical element C is not causally connected with 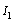 , we can write
, we can write 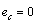 . The corresponding vector is
. The corresponding vector is 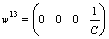 . Thus, we have
. Thus, we have 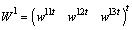 and
and 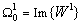 .Same calculation is carried out for the three other modes. We obtain
.Same calculation is carried out for the three other modes. We obtain 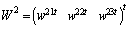 ,
, 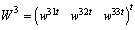 and
and 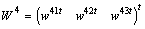 , with
, with 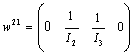 ,
, 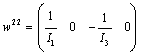 ,
, 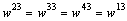 ,
, 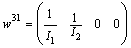 ,
, 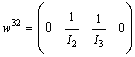 ,
, 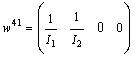 and
and 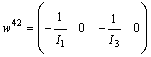 .We have
.We have 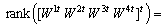

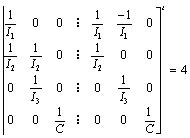 The system is structurally observable.Remark 3 If these conditions are not checked, it is necessary to use a necessary and sufficient condition. This result will be done in a future work.
The system is structurally observable.Remark 3 If these conditions are not checked, it is necessary to use a necessary and sufficient condition. This result will be done in a future work.6. Conclusions
- The structural observability property of controlled switching linear systems is studied using simple causal manipulations on the bond graph model. Thus, formal calculation enables us to know the reachable variables; its checking is immediate on the bond graph model in integral causality. On the other hand the bond graph model in derivative causality enables us to characterize graphically the structural observability subspaces relating to each mode. Two sufficient conditionswas given by exploiting these various bases. Finally procedures were proposed. In fact, the proposed method, based on a bond graph theoretic approach, assumes only the knowledge of the systems structure. The subspaces can be employed to propose structured state feedback matrices in the context of pole assignment by static state feedback. This result can be implemented by classical bond graph theory.
ACKNOWLEDGEMENTS
- The author expresses his thanks to the reviewers who made suggestions that helped to improve the presentation of this paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML