A. Ikhlef 1, N. Mansouri 2
1Laboratoire d’Automatique et de Robotique, Département d’électronique, Université Mentouri Constantine
2Route de Ain-El-Bey., 25000. Constantine, Algérie
Correspondence to: N. Mansouri , Route de Ain-El-Bey., 25000. Constantine, Algérie.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper addresses the hyperchaotification and the synchronization of chaotic systems. A nonlinear state feedback controller was designed to generate hyperchaos from the original chaotic system. The hyperchaos was identified by the existence of two positive Lyapunov exponents, bifurcation diagram and phase diagrams. Furthermore, effective active controllers are designed for synchronizing the obtained hyperchaotic system with different chaotic systems. To illustrate the effectiveness of the proposed approach, numerical simulation results obtained with the Lü and Qi chaotic systems are given.
Keywords:
Synchronisation, Active Control, Hyperchaotification
1. Introduction
Chaos has been extensively studied within the scientific, engineering and mathematical communities as an interesting complex dynamic phenomenon. Recently, the traditional trend of understanding and analysing chaos has evolved to a new phase of investigation: controlling and creating chaos. More specifically, when chaos is useful, it is generated intentionally. However, when chaos is harmful, it is controlled[1-4].Indeed, several studies have showed that chaos can be useful or has great potential in many disciplines and most of the developed methods concern with the chaotic synchronization[5-8]. Pecora and Carroll[5] suggested that the phenomenon of chaos synchronism may serve as the basis for new ways for achieving secure communication. Since, many techniques have been proposed in order to hide the contents of a message by exploiting chaotic systems. Perez and Cerderia have proved that messages masked by simple chaotic processes can be easily extracted once intercepted[9]. After, Pecora proved that this problem can be solved by using higher dimensional hyperchaotic systems[10]. This consideration has led to the development of interesting techniques for hyperchaos synchronization[11,12]. Hyperchaotic systems have the characteristics of high security and high efficiency. They can be broadly applied in nonlinear circuits, secure communications, biological systems and many other fields.In this paper, we are interested in the hyperchaotification and synchronization of chaotic systems. The hyperchaotification is obtained using a delay feedback control algorithm.It is based on the idea that hyperchaotic systems are usually defined as chaotic systems with more than one positive Lyapunov exponent. A closed form expression was provided for the controller, in terms of the system state vector and a set of Lyapunov exponents. Simultaneously, the controlled system is synchronized with a second chaotic system, by applying an algorithm based on the active control theory.The paper is organized as follows: In section 2, we introduce the hyperchaotification algorithm and its application to the Lü system. In section 3, the proposed synchronization algorithm is detailed on chaotic and hyperchaotic systems and we provide some simulation results obtained with the Lü and Qi systems. These results illustrate the effectiveness of the proposed procedure.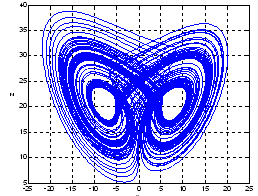 | Figure 1. Attractors of the Lü system for 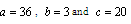 |
2. Hyperchaotification of Lü System
The Lü system is described by the following equations: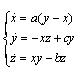 | (1) |
Where ,and represent the system parametersThe system of differential equations is integrated using the fourth order Runge-Kutta method. For: 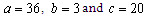 , the Lyapunov exponents, are
, the Lyapunov exponents, are 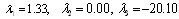 We deduce that for these values, the system is chaotic since one of the exponents is positive and the system exhibits a chaotic behaviour, as shown in Fig. 1.For the hyperchaotification of a chaotic system, the two following conditions must be verified:The dimension of the system must be at least equal to 4 and the order of the state equation must be at least 2.The system must have at least two positive Lyapunov exponents and the sum of all the exponents must be negative.For this, the hyperchaotification of the Lü chaotic system consists to increase the dimension of the system by adding an equation representing a state feedback controller in the state equations system. Some authors suggested to construct a hyperchaotic attractor of the Lü system by adding the state feedback controller
We deduce that for these values, the system is chaotic since one of the exponents is positive and the system exhibits a chaotic behaviour, as shown in Fig. 1.For the hyperchaotification of a chaotic system, the two following conditions must be verified:The dimension of the system must be at least equal to 4 and the order of the state equation must be at least 2.The system must have at least two positive Lyapunov exponents and the sum of all the exponents must be negative.For this, the hyperchaotification of the Lü chaotic system consists to increase the dimension of the system by adding an equation representing a state feedback controller in the state equations system. Some authors suggested to construct a hyperchaotic attractor of the Lü system by adding the state feedback controller  on the state
on the state  . In our case, we choose to introduce it on y, as follows:
. In our case, we choose to introduce it on y, as follows: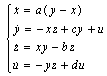 | (2) |
The fixed points are obtained by solving: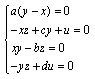 | (3) |
And the jacobian matrix of the system is given by: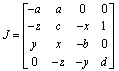 | (4) |
This implies that the stability around the fixed points is function of (a, b, c) and also d.Assume that the Lyapunov exponents of the controlled chaotic Lü system are λi (i = 1,...,4) satisfying λ1 > λ2> λ3> λ4, then the dynamical behaviours of the system can be classified as follows:For λ1>0; λ2 = 0, λ4 < λ3<0 and λ1 + λ3+ λ4 <0, the system is chaotic.For λ1> λ2 > 0; λ3=0, λ4 < 0 and λ1 + λ2+ λ3+ λ4 <0, the system is hyperchaotic.For λ1=0; λ4 < λ3 < λ2<0, the system is periodicThe analysis of the dynamic behaviour of this system is done using the bifurcation diagram and the Lyapunov exponents computed with a=36, b=36, c=20, and by increasing the parameter d.| Table 1. Lyapunov Exponents for different values of d |
| | d | λ1 | λ2 | λ3 | λ4 | | -5 | 1.189 | 0.005 | -4..321 | -20.810 | | -1.5 | 0.001 | -0.120 | -0.157 | -20.202 | | 0.1 | 0.785 | -0.001 | -0.342 | -19.305 | | 1.8 | 0.978 | 0.197 | -0.004 | -18.330 |
|
|
Table 1 gives the obtained Lyapunov exponents. We note that:For d=-5 and d= 0.1, we have λ1>0; λ2 ≅ 0, λ4 < λ3<0 and λ1+ λ3+ λ4 <0 ⇒ the system is chaotic.For d=-1.5; λ1 ≅ 0; λ4 < λ3 < λ2<0⇒the system is periodicFor d=1.8, λ1> λ2>0; λ3 ≅ 0, λ4 <0 and λ1+λ2+ λ4<0⇒the system becomes hyperchaoticThe bifurcation diagram in the y-d plan, where represents the Poincaré section, is given in Fig. 2. It shows that the system evolves from chaotic state to periodic orbit and from periodic orbit to chaotic, then hyperchaotic state.We can conclude that for some values of d, this method of control stabilizes the initial chaotic system. However, if this parameter continues to increase, a hyperchaotic behaviour appears.Fig 3. to Fig. 5. show the behaviour in the phase plane, of the controlled Lü system for different values of d.In Fig. 5 we can notice that the obtained hyperchaotic attractor has a similar form that the original Lü system with the appearance of additional branches which characterizes the hyperchaotic dynamic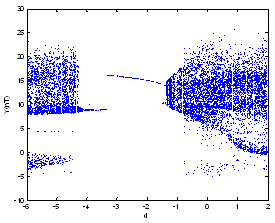 | Figure 2. Bifurcation diagram of the controlled Lü system |
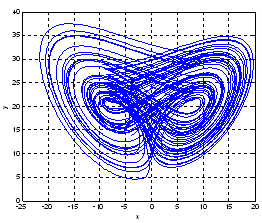 | Figure 3. Chaotic attractor of the modified Lü system for d=-5 |
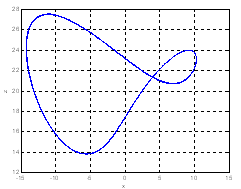 | Figure 4. Periodic orbit of the controlled Lü system for d=-1.5 |
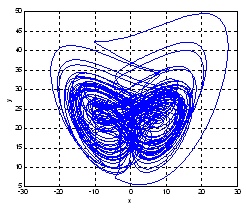 | Figure 5. Hyperchaotic attractor of the controlled Lü system for d=1.8 |
3. Synchronization of Hyperchaotic and Chaotic Systems
Many effective methods have been presented to synchronize chaotic systems. Synchronization is always done between a system designed as master and another as slave. The principle of synchronization is to apply on the slave a control function, such as the error between the two systems tends to zero. The problem can then be expressed as a problem of control that consists of minimizing the error between the master and the slave by applying the control law. In our case we use an active control algorithm.In the following, we consider the synchronization of the hyperchaotic Lü system with a chaotic system, by applying an algorithm based on the active control theory. The hyperchaotic system is considered as master and the chaotic system as slave.
3.1. Synchronization of the Hyperchaotic LÜ System and the 4D Chaotic LÜ System
The master system is given by: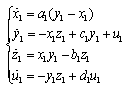 | (5) |
And the slave by: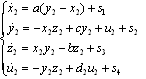 | (6) |
Where: S=[s1, s2, s3, s4]T represents the active control function to be designed. The control function is composed of two parts: one non linear for eliminating non linear term and a linear part to ensure the stability of the obtained system. The error between the master and the slave is given by: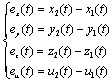 | (7) |
And its dynamic by: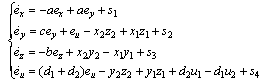 | (8) |
For the synchronization of the two systems, we must have: 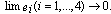 In order to eliminate the nonlinear terms, we choose:
In order to eliminate the nonlinear terms, we choose: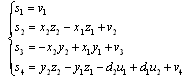 | (9) |
So, the system to be controlled is a linear system with a control input v1, v2, v3, and v4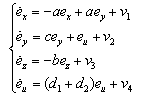 | (10) |
These equations converge to zero, if we choose a control law, which ensures that all the eigenvalues will be in the left part of the complex plan. So, we assume that: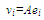 | (11) |
Several choices are possible, in particular: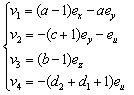 | (12) |
In this case, all the eigenvalues are equals to -1 and the error 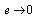 when
when 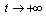 .For the simulation, we choose the master system as the new hyperchaotic Lü system with d1=1.8. The same system with d2=-5 is considered as the chaotic slave systemFor the others parameters, we assume that:a1 =a2=a=36, b1 =b2=b=3, c1 =c2=c=20.Fig.(6-a) to Fig.(6-d) represent the results of the synchronization when the control is actived at t=2s and initial conditions for the master and the slave, as follows:x1(0)=0.1, y1(0)=1, z1(0)=0.2, u1(0)=0.1x2(0)=-20, y2(0)=30, z2(0)=-8, u2(0)=5We notice that the trajectories converge rapidly and become identical in a short time
.For the simulation, we choose the master system as the new hyperchaotic Lü system with d1=1.8. The same system with d2=-5 is considered as the chaotic slave systemFor the others parameters, we assume that:a1 =a2=a=36, b1 =b2=b=3, c1 =c2=c=20.Fig.(6-a) to Fig.(6-d) represent the results of the synchronization when the control is actived at t=2s and initial conditions for the master and the slave, as follows:x1(0)=0.1, y1(0)=1, z1(0)=0.2, u1(0)=0.1x2(0)=-20, y2(0)=30, z2(0)=-8, u2(0)=5We notice that the trajectories converge rapidly and become identical in a short time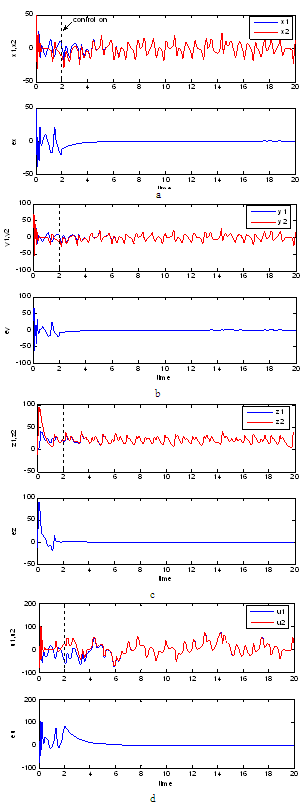 | Figure 6. Synchronization of different state variables |
3.2. Synchronization of the Hyperchaotic LÜ System and the 3D Chaotic LÜ System
 | Figure 7. Synchronization of different state variables |
The master system is the same as for the previous case and the slave system is given by: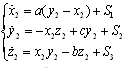 | (13) |
Where 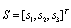 represents the active control function to design.The error between the master and the slave is given by:
represents the active control function to design.The error between the master and the slave is given by: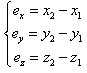 | (14) |
And its dynamic, by: 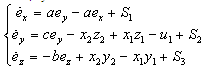 | (15) |
The control law consists of two parts: A part to eliminate the nonlinear terms and another to stabilize the resulting linear system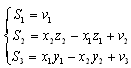 | (16) |
So, the controlled system is as follows: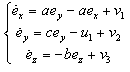 | (17) |
With: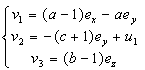 | (18) |
In Fig. 7(a-c), the trajectories of the two systems are initially completely different due to the sensitivity to the initial conditions. Once activated the control at t=2s, the two systems take a short time to be perfectively synchronized. The trajectory of the chaotic slave system become the same as that of the master hyperchaotic system
3.3. Synchronization of the Hyperchaotic Lü System and the Qi Chaotic System
In this example, the master system is the hyperchaotic Lü system, and the slave system is the Qi chaotic system. This implies that when the two systems are synchronized, the Qi chaotic system will follow the same trajectories as those of the hyperchaotic Lü system. The Qi system is defined by: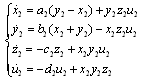 | (19) |
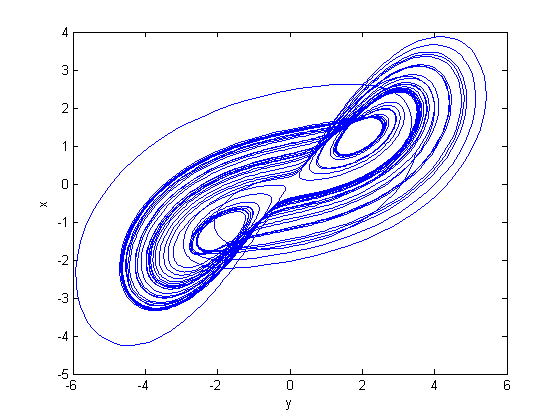 | Figure 8. Chaotic Attractor of the Qi system |
For a2=30, b2=10, c2=1 and d2=10 the system has a chaotic behaviour. Fig. 8. shows the chaotic attractor obtained from the following initial conditions: x2(0) = 0.15, y2(0) = 1.1, z2(0) = 0.25, u2(0)=0.15. As for the previous example, we define the master system: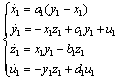 | (20) |
And the slave system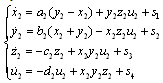 | (21) |
The active control function applied on the slave is: 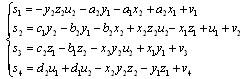 With:
With: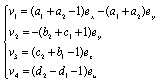 | (22) |
Fig.(9-a) to (9-d) represent the simulation results for this case. The chaotic slave system becomes hyperchaotic although it is different from the master system. These results demonstrate the effectiveness of the described algorithm even when the two systems are different and the slave system is strongly nonlinear. The controller drives the chaotic system to hyperchaotic trajectories 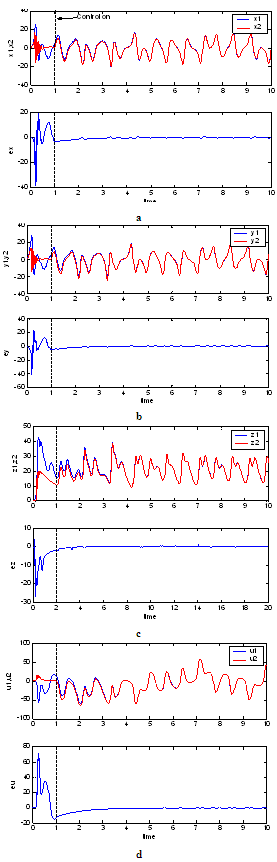 | Figure 9. Synchronization of different state variables |
4. Conclusions
In this paper, we introduced the generation of new hyperchaotic Lü system. Dynamical behaviours of the system are explored by calculating the Lyapunov exponents and the phase diagram. The synchronization of the obtained hyperchaotic system with a chaotic system is possible using an active control algorithm. In addition to its efficiency, this method is easy to implement and achieves the synchronization of two systems completely different, in a reduced time. The stability is guaranteed since the control law ensures that the eigenvalues of the system are always in the left part of the complex plan.
References
| [1] | E. Ott, C. Grebogi and J. A. York, “Controling chaos,” Phys. Rev. Lett., Vol. 64, No. 11, pp. 1196-1199, 1990. |
| [2] | M. Chen and Z. Han, “An iteration method for chaotifying and controlling dynamical systems,” Int. J. Bifurcation and Chaos, Vol. 12, pp. 1173-1180, 2002. |
| [3] | L. Tam, J. Chen, H. Chen and W. Tou, “Generation of hyperchaos from the Chen–Lee system via sinusoidal perturbation,” Chaos, Solitons and Fractals, Vol. 38, pp. 826-839, 2008. |
| [4] | X. Wu, J. Lu, H. Lu and S. Wong, “suppression and generation of chaos for a three-dimensional autonomous system using parametric perturbations,” Chaos, Solution and Fractals, pp. 811-819, 2007. |
| [5] | T. L. Carroll and L. M. Pecora, “Synchronizing chaotic circuits”, IEEE Trans. on CAS, Vol. 38, No.4, pp. 453-456, 1991. |
| [6] | Y. Zou, J. Zhu, G. Chen and X. Luo, “ Synchronization of hyperchaotic oscillators via single unidirectional chaotic-coupling,” Chaos, Solitons and Fractals, Vol. 25, pp. 1245-1253, 2005. |
| [7] | S. Bowong, “Adaptive synchronization between two different chaotic dynamical systems,” Communications in Nonlinear Science and Numerical Simulation, 12, pp. 976-985, 2007. |
| [8] | Q. Zhang and J. Lu, “Chaos synchronization of new chaotic system via nonlinear control,” Chaos, Solution and Fractals, Vol. 37, pp. 175-179, 2008. |
| [9] | G. Perez and H. Cerderia, “Extracting message masked by chaos,” Phys. Rev. Lett, Vol. 74, pp. 1970-1973, 1995. |
| [10] | L. Pecora, “ Hyperchaos harnessed”, Phys. World 9, pp. 17-17,1996. |
| [11] | A. Chen, J. Lu, J. Lü and S. Yu, “generating hyperchaotic Lü attractor via state feedback control,” Phys. A. 364, pp. 103-110, 2006. |
| [12] | Q. Jia, “Hyperchaos generated from Lorenz chaotic system and its control,” Phys. Lett. A, Vol. 366, pp. 217-222, 2007. |


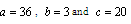
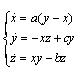
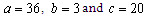 , the Lyapunov exponents, are
, the Lyapunov exponents, are 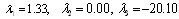 We deduce that for these values, the system is chaotic since one of the exponents is positive and the system exhibits a chaotic behaviour, as shown in Fig. 1.For the hyperchaotification of a chaotic system, the two following conditions must be verified:The dimension of the system must be at least equal to 4 and the order of the state equation must be at least 2.The system must have at least two positive Lyapunov exponents and the sum of all the exponents must be negative.For this, the hyperchaotification of the Lü chaotic system consists to increase the dimension of the system by adding an equation representing a state feedback controller in the state equations system. Some authors suggested to construct a hyperchaotic attractor of the Lü system by adding the state feedback controller
We deduce that for these values, the system is chaotic since one of the exponents is positive and the system exhibits a chaotic behaviour, as shown in Fig. 1.For the hyperchaotification of a chaotic system, the two following conditions must be verified:The dimension of the system must be at least equal to 4 and the order of the state equation must be at least 2.The system must have at least two positive Lyapunov exponents and the sum of all the exponents must be negative.For this, the hyperchaotification of the Lü chaotic system consists to increase the dimension of the system by adding an equation representing a state feedback controller in the state equations system. Some authors suggested to construct a hyperchaotic attractor of the Lü system by adding the state feedback controller 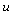 on the state
on the state 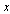 . In our case, we choose to introduce it on y, as follows:
. In our case, we choose to introduce it on y, as follows: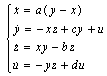
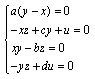
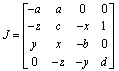




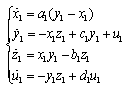
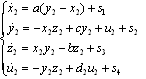
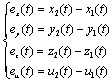
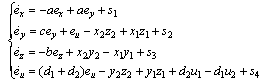
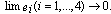 In order to eliminate the nonlinear terms, we choose:
In order to eliminate the nonlinear terms, we choose: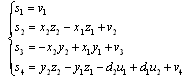
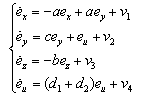
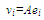
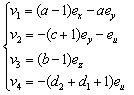
 when
when 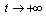 .For the simulation, we choose the master system as the new hyperchaotic Lü system with d1=1.8. The same system with d2=-5 is considered as the chaotic slave systemFor the others parameters, we assume that:a1 =a2=a=36, b1 =b2=b=3, c1 =c2=c=20.Fig.(6-a) to Fig.(6-d) represent the results of the synchronization when the control is actived at t=2s and initial conditions for the master and the slave, as follows:x1(0)=0.1, y1(0)=1, z1(0)=0.2, u1(0)=0.1x2(0)=-20, y2(0)=30, z2(0)=-8, u2(0)=5We notice that the trajectories converge rapidly and become identical in a short time
.For the simulation, we choose the master system as the new hyperchaotic Lü system with d1=1.8. The same system with d2=-5 is considered as the chaotic slave systemFor the others parameters, we assume that:a1 =a2=a=36, b1 =b2=b=3, c1 =c2=c=20.Fig.(6-a) to Fig.(6-d) represent the results of the synchronization when the control is actived at t=2s and initial conditions for the master and the slave, as follows:x1(0)=0.1, y1(0)=1, z1(0)=0.2, u1(0)=0.1x2(0)=-20, y2(0)=30, z2(0)=-8, u2(0)=5We notice that the trajectories converge rapidly and become identical in a short time

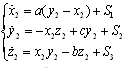
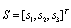 represents the active control function to design.The error between the master and the slave is given by:
represents the active control function to design.The error between the master and the slave is given by: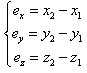
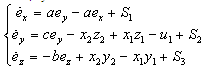
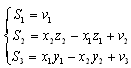
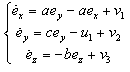
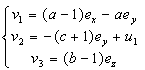
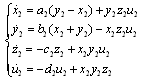

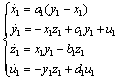
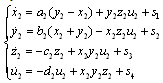
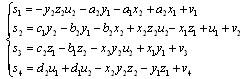 With:
With: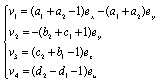

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML