1. Introduction

Spectral methods using expansion in orthogonal polynomials such as Chebyshev polynomials have proven successful in the numerical approximation of various boundary value problems; see for instance[12]. If these polynomials are used as basis functions, then the rate of decay of the expansion coefficients is determined by the smoothness properties of the function being expanded[17]. This choice of trial functions is responsible for the superior approximation properties of spectral methods when compared with finite difference and finite element methods[2]. For spectral and pseudospectral methods, explicit expressions for the expansion coefficients of the derivatives in terms of the expansion coefficients of the solution are needed. Infinite-horizon Pontryagin's principle has been introduced early in[1]. The authors in[6] introduced a Chebyshev spectral procedure for solving optimal control problems.

In[3], the author obtained a general formula when the basis functions are the Ultraspherical polynomials, while Chebyshev and Legendre pseudospectral approximations are used to solve integral and integro-differential equations in[4] and[8], respectively.

It should be mentioned that the study of the existence and the structure of solutions of optimal control problems defined on finite intervals has recently been a rapidly growing area of research. See, for example,[7,9,11,14] and the references mentioned therein. A variety of numerical methods for solving infinite horizon variational optimal control problem exists in[15] and[18].

Some kind of optimal control problems which are governed by ordinary differential equations are discussed in[5, 16]. Linear quadratic optimal control problem is solved by using Legendre approximation[10].The most common approach is to replace the unknowns of the problem by some approximation function and determine the unknowns by minimizing the resulting constrained optimization problem. The time optimal boundary control of a one-dimensional vibrating system subject to a control constraint that prescribes an upper bound for the -norm of the image of the control function under a Volterra operator[13].

The proposed algorithm describes an alternative technique. The system dynamics can be approximated by transforming the boundary value problem for ordinary differential equations into integral formulas. Start with a Legendre spectral approximation for the highest-order derivative and generate approximations to the lowest-order derivatives through successive integrations. Therefore, the differential and integral expressions that arise in the system dynamics, the performance index and the initial (or boundary) conditions (and even for general multipoint boundary conditions) are converted into algebraic equations with unknown coefficients. This algorithm is of the finite element type and results in static optimization problems with a relatively small number of variables. This means that the optimal control problem is reduced to a parameter static optimization problem, which consists of the minimization of an objective function, subject to a system of algebraic constraints that are linear in the state variables, irrespective of whether the dynamic system itself is linear or nonlinear. In such cases, the static optimization problem can be efficiently performed using the penalty partial quadratic interpolation (PPQI) technique[5]. We derived error estimation of this approximation, and introduced an algorithm that gives an optimal approximation of the integrals.

The paper is organized as follows: In section 2, we introduce mathematical formulation of optimal control problem with linear terminal constraints. In section 3,a Legendre approximate solution is presented. In section 4, error bounds for Legendre method is explained. In section 5, some numerical examples are given to clarify the proposed method and compared with other methods. Finally, in section 6 some remarks and conclusions of the work are presented.

2. Setting Optimal Control Problems With Linear Terminal Constraints

Due to the global nature of the smooth functions, spectral methods are usually global methods, i.e. the value of a derivative at a certain point in space depends on the solution at all the other points in space, and not just the neighboring grid points. Due to this fact, spectral methods usually have a very high order of approximation. Spectral convergence meaning that the error is in fact decreasing exponentially as opposed to algebraically as for finite-difference methods.

Spectral methods usually give the exact derivative of a function; the only error is due to the truncation to a finite set of smooth functions/coefficients. On the other hand, spectral methods are geometrically less flexible than lower-order methods, and they are usually more complicated to implement. Additionally, the spectral representation of the solution is difficult to combine with sharp gradients, e.g. problems involving shocks and discontinuities.

In the next section, optimal control problems with spectral methods are very adapted and efficient discretization schemes. Now, consider the problem of finding the control 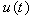which minimizes the cost functional:

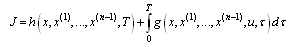(2.1)

Subject to

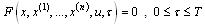(2.2)

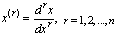where and the linear initial constraints,

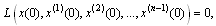(2.3)

and the terminal constraints,

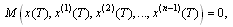(2.4)

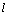where the time T is assumed to be fixed, L and M are vector functions of dimension and 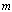, respectively, with 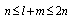. The state variable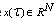, the control variable 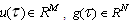are real valued continuous functions on.

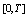To change the time interval 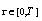into 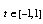, we have:

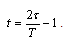Hence the optimal control problem becomes:

Minimize

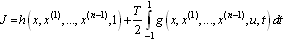(2.5)

Subject to

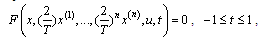(2.6)

and the linear initial and terminal constraints,

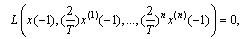(2.7)

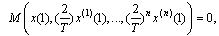(2.8)

3. Pseudospectral Legendre Integration Differentiation Matrices

We present here the Legendre approximations of any function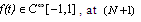, Legendre-Gauss-Lobatto (LGL) points as follows:

Let 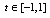such that .

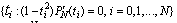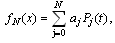(3.1)

where

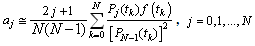(3.2)

Approximate the integrals of a function as follows:[7]

,

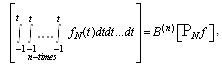where the elements of 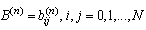are given by: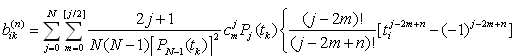

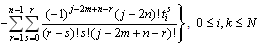(3.3)

and

.

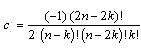4. Legendre Approximations for OCP

Legendre approximations are adopted here to approximate the solution of the problem. We start with Legendre approximations for the highest-order derivative, 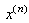, and generate approximations to the lowest-order derivatives 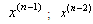;…and 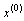, through successive integrations of the highest-order derivative.

Suppose that

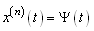(4.1)

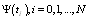where are some unknowns. By integration, and making use of the given conditions, we get

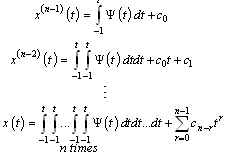(4.2)

Now we apply our Legendre integral approximation:

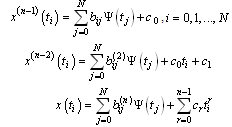(4.3)

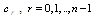where the constants may be defined from the given conditions. Making use of the approximation for the control variable as 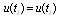, the optimal control problem (2.5)-(2.8) are replaced by the following constrained optimization problems:

Minimize

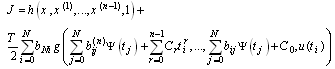(4.4)

Subject to

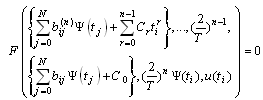(4.5)

The constrained optimization problem is then takes the form:

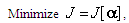(4.6)

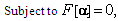(4.7)

where .

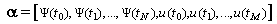The problem (4.6)–(4.7) is solved by using penalty partial quadratic interpolation technique[5]. We therefore use:

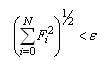to decide whether the computed solution in close enough to the optimal solution.

5. Error Estimation

In this section, an estimation of the error bound of the Legendre integration method is presented in the flowing theorem.

Theorem (5.1)[8]

Let 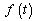be approximated by Legendre polynomials, then there exists a number 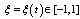such that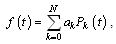

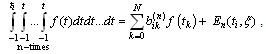(5.1)

where

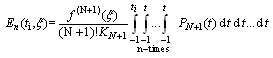(5.2)

and

.

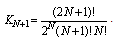The following theorem gives the error bounds of the system dynamic.

Theorem (5.2)

Assume the OCP (2.5)-(2.8) is approximated by Legendre approximations and assuming that 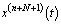is bounded i.e.

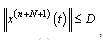(5.3)

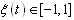then there exists a number such that

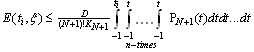(5.4)

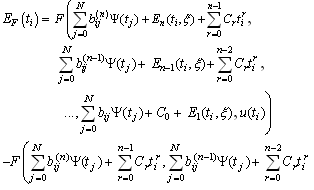
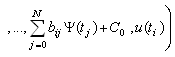(5.5)

Proof:

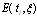Let denote the error in approximation 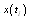with (4.3), namely

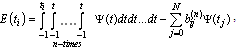(5.6)

then, making use of (5.1) and (5.2), the error in the approximation (4.3) can be written as:

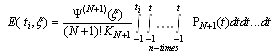
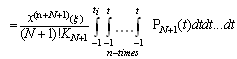Thus, making use of (5.3), we get

.

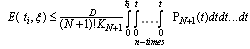The original constraint (2.6) in view of (4.2) becomes:

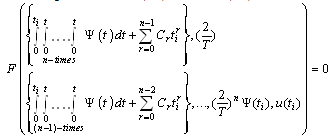Making use of (5.1) then,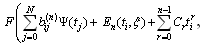

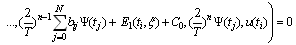(5.7)

Subtracting (4.5) from (5.7), we obtain

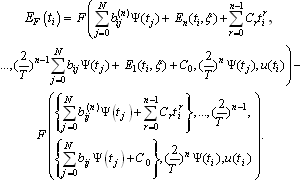with 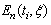is defined in (5.2).

6. Numerical Examples and Application

Now, we consider the following problems to show the effectiveness of our technique.

Example 1:

Among all piecewise differentiable control variables, find the optimal control 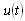which minimizes

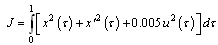(6.1)

Subject to:

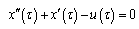(6.2)

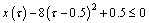(6.3)

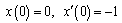(6.4)

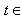The first step in solving this problem by the proposed method is to transform the time interval into [-1, 1]. At the end, this will lead to the following problem.

Minimize

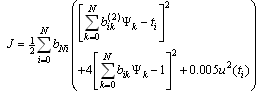(6.9)

Subject to:

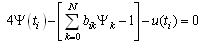(6.10)

We approximate the inequality constraint by adding slack variables:

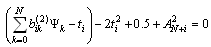(6.11)

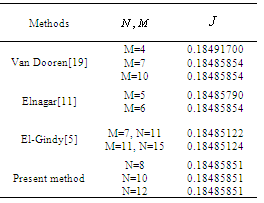
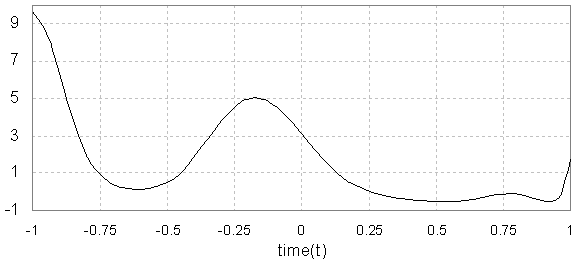
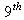Solving this problem (6.9)-(6.11) by using the proposed method by order Legendre, we find the optimal value is 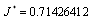. The optimal state and control are shown in Figs. (1) and (2), respectively. The author in[8] used of cell averaging Chebyshev method by order Chebyshev for solve this example and get .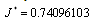

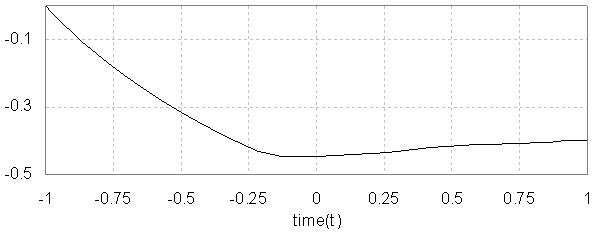Figure 1. state variable x(t) of example(1)

Figure 2. control varaible u(t) of example(1)

Example 2: The Controlled Linear Oscillator

Consider the optimal control problem of a liner oscillator the performance index

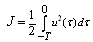(6.12)

is minimized over all admissible control functions .

Subject to the differential equation

(6.13)

with the boundary conditions

.

The problem can be converted to the following constrained optimization problem: Minimize

(6.17)

Subject to

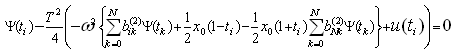(6.18)

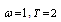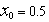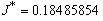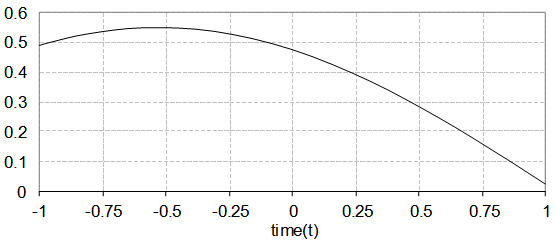
At and , we get the optimal result with . Table (1) gives the optimal values of the cost functional for different values of . The state and control variables are shown in Figs. (3) and (4), respectively.

Table 1.       of present method with other methods

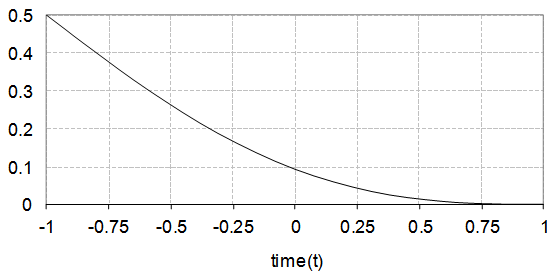Figure 3. State varible x(t) of example (2)

Figure 4. control variable u(t) of example (2)

Example (3) Find a suitable control for minimization of the following optimal control problem[24]:

Minimize

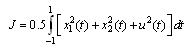Subject to:

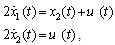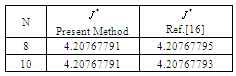
with the boundary conditions: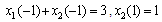

.

By apply the proposed method; the optimal values of state and control given in Table (2). Table (3) shows that the presented Legendre approximations are more efficiency than the method in[16].

Table 2. Observed state x(t) and control u(t) variables for Example(3) T χ1(t) χ2(t) u(t) -1.000 1.21 1.79 -2.422 -0.951 1.195 1.732 -2.32 -0.809 1.158 1.578 -2.038 -0.588 1.118 1.375 -1.635 -0.309 1.099 1.179 -1.179 0.000 1.123 1.033 -0.725 0.309 1.196 0.953 -0.307 0.588 1.309 0.936 0.051 0.809 1.435 0.957 0.331 0.951 1.534 0.987 0.512 1.000 1.571 1 0.575

Table 3. Comparison with results in Ref.[16]

Table 4. State and control variables for Example (4) t χ1(t) χ2(t) u(t) -1.000 -5 -5 2.767 -0.951 -5.255 -3.312 5.568 -0.809 -5.432 1.043 3.152 -0.588 -4.627 4.081 0.881 -0.309 -3.101 4.388 0.405 0.000 -1.522 3.68 -0.591 0.309 -0.321 2.528 -1.097 0.588 0.423 1.845 -0.585 0.809 0.91 1.736 -0.132 0.951 1.226 1.846 0.089 1.000 1.341 1.892 0.057

Example (4) Find a suitable control for minimization of the following optimal control problem:

Minimize

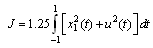Subject to: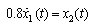

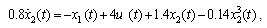and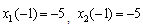

.

The optimal cost is 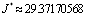as given in[9]. Table (4) shows the state and control variables as computed by the proposed method.

Table 5. Comparison with results in Ref.[11]

The major advantages of this method is that, we can deal directly with the highest-order derivatives in the differential equation without transforming it to a system of first order, and that will reduce the number of the unknowns. The tables show that the suggested technique is quite reliable. The methods produce an accurate solution at small number of nodes. The comparison of the maximum absolute error resulting from the proposed method and those obtained by[5],[11] and[19] show favourable agreement and always it is more accurate than these treatments.

7. Conclusions

The basic idea of our present method is to transform the optimal control problems governed by ordinary differential equations to a constrained optimization problem, by using Legendre approximation method. We solve the resulting constrained optimization problem since it is easier than solving the original problem. Here we used (PPQI) method, which may be more suitable in such case, where the number of constraints is increases. Finally, the method has been extended to the linear and nonlinear optimal control problems.