-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
2012; 2(3): 47-53
doi: 10.5923/j.control.20120203.05
Adaptive Dynamic Surface Control: Stability Analysis Based on LMI
Bongsob Song
Department of Mechanical Engineering, Ajou University, Suwon, 443-749, Korea (ROK)
Correspondence to: Bongsob Song, Department of Mechanical Engineering, Ajou University, Suwon, 443-749, Korea (ROK).
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, quadratic stability of adaptive dynamic surface control for a class of nonlinear systems in strict-feedback form is analyzed in the framework of linear matrix inequality. While the existence of controller gains and filter time constants for semi-global stability was theoretically proved in the literature, it is not sufficient to describe how a set-point value and parameter update laws affect stability and parameter convergence. Thus, it is necessary to provide a systematic analysis method to guarantee both stability and parameter convergence. By deriving the augmented closed-loop error dynamics in linear differential inclusion form, a sufficient condition of the controller gains for stability and parameter convergence is derived in the form of linear matrix inequality. Finally, the quadratic Lyapunov function for its quadratic stability is computed numerically via convex optimization.
Keywords: Adaptive Dynamic Surface Control, Quadratic Stability, Parameter Convergence, Linear Matrix Inequality
Article Outline
1. Introduction
- The dynamic surface control (DSC) is a dynamic extension of multiple sliding surface (MSS) control to overcome the drawback of "explosion of complexity" in backstepping as well as MSS control[1]. The use of a series of dynamic filters enables the controller to be designed sequentially and simple. Furthermore, the existence of controller gains for semi-global stability was theoretically proved in[1]. Recently, an analysis and design method in the framework of convex optimization has been introduced to allow us to find a quadratic Lyapunov function numerically for a class of nonlinear systems called strict-feedback form[2]. This control approach was extended to a class of nonlinear systems where the uncertainty is linearly parameterized, e.g.,
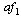 in (1) where a is an unknown constant and f1 is a known nonlinear function. The adaptive backstepping method has been developed[3] and extended to a class of time-delay nonlinear systems[4, 5]. As introduced above, the adaptive DSC to solve the problem of "explosion of complexity" has been developed for a class of nonlinear systems and time-delay systems[6, 7]. Furthermore, DSC has been combined with adaptive neural network control scheme in the literature[8, 9]. However, the useful tools such as linear matrix inequalities (LMIs) are hard to apply to nonlinear system with linearly parameterized uncertainties. There is little work in the literature for LMIs to be used for stability analysis of adaptive nonlinear control problems.The following example illustrates the design procedure of adaptive dynamic surface control in[6]:
in (1) where a is an unknown constant and f1 is a known nonlinear function. The adaptive backstepping method has been developed[3] and extended to a class of time-delay nonlinear systems[4, 5]. As introduced above, the adaptive DSC to solve the problem of "explosion of complexity" has been developed for a class of nonlinear systems and time-delay systems[6, 7]. Furthermore, DSC has been combined with adaptive neural network control scheme in the literature[8, 9]. However, the useful tools such as linear matrix inequalities (LMIs) are hard to apply to nonlinear system with linearly parameterized uncertainties. There is little work in the literature for LMIs to be used for stability analysis of adaptive nonlinear control problems.The following example illustrates the design procedure of adaptive dynamic surface control in[6]: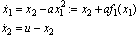 | (1) |
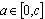 and
and 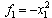 is a known nonlinear function and locally Lipschitz on
is a known nonlinear function and locally Lipschitz on 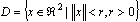 , i.e.,
, i.e.,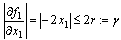 Where y is a Lipschitz constant. The control objective is
Where y is a Lipschitz constant. The control objective is 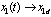 where x1d is a constant with
where x1d is a constant with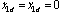 , which is called a set-point control problem.First, define the first error surface as
, which is called a set-point control problem.First, define the first error surface as 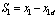 . After taking its derivative along the trajectories of (1)
. After taking its derivative along the trajectories of (1)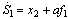 ,the synthetic input, which is to drive
,the synthetic input, which is to drive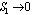 , is
, is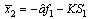 | (2) |
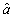 is the estimate of the unknown parameter a following the update law as propose in[6]:
is the estimate of the unknown parameter a following the update law as propose in[6]: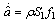 | (3) |
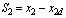 where x2d equals
where x2d equals 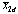 passed through a first-order filter, i.e.,
passed through a first-order filter, i.e.,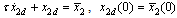 | (4) |
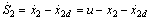 ,and the control input is derive as
,and the control input is derive as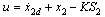 | (5) |
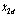 is calculated from (4) such that
is calculated from (4) such that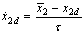 .It is interesting to remark that the calculation of
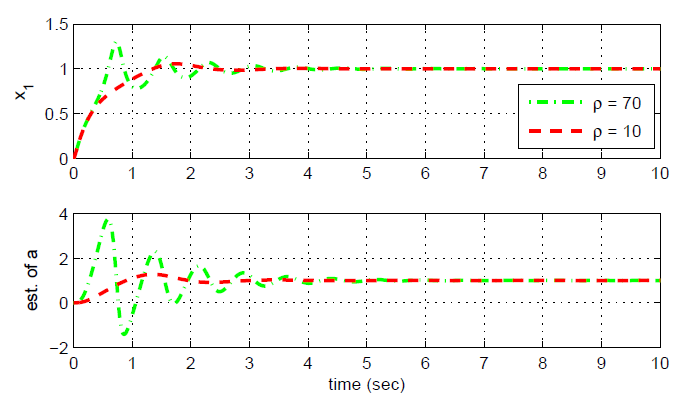
.It is interesting to remark that the calculation of  becomes simpler due to the inclusion of the first-order filter while it results in "explosion of complexity" in backstepping.A next question is how to design a set of controller gains to guarantee stability, e.g., K, τ and ρ in the example. It was proven in[6] that there exist a set of controller gains (K and τ) to guarantee the stability for stabilization and set-point control problems. However, the performance of the adaptive DSC depends on ρ critically[10]. If a small magnitude of ρ is chosen, the adaption of a in (3) will be slow and the transient error will be large. On the other hand, too large magnitude of ρ will lead to oscillatory estimation of the parameter, thus resulting in the oscillatory error.Suppose a = 1 in (1), K = 2.5 in (2) and (5), and τ = 0.05 in (4). When ρ is assigned as 1 and 10 respectively, the time responses of x1 and
becomes simpler due to the inclusion of the first-order filter while it results in "explosion of complexity" in backstepping.A next question is how to design a set of controller gains to guarantee stability, e.g., K, τ and ρ in the example. It was proven in[6] that there exist a set of controller gains (K and τ) to guarantee the stability for stabilization and set-point control problems. However, the performance of the adaptive DSC depends on ρ critically[10]. If a small magnitude of ρ is chosen, the adaption of a in (3) will be slow and the transient error will be large. On the other hand, too large magnitude of ρ will lead to oscillatory estimation of the parameter, thus resulting in the oscillatory error.Suppose a = 1 in (1), K = 2.5 in (2) and (5), and τ = 0.05 in (4). When ρ is assigned as 1 and 10 respectively, the time responses of x1 and  are shown is Fig. 1. As explained above, the larger magnitude of ρresults in faster convergence of estimation error of
are shown is Fig. 1. As explained above, the larger magnitude of ρresults in faster convergence of estimation error of 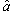 and tracking error. However, when ρ = 70, the oscillatory estimation of the parameter is shown in Fig. 1. Thus, the tracking error does not converge to zero. Furthermore, if x1d is changed to a different constant, although it will be discussed later in Section 4, the different time response (e.g., oscillatory estimation) of
and tracking error. However, when ρ = 70, the oscillatory estimation of the parameter is shown in Fig. 1. Thus, the tracking error does not converge to zero. Furthermore, if x1d is changed to a different constant, although it will be discussed later in Section 4, the different time response (e.g., oscillatory estimation) of 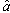 may be shown for the same set of K, τ, and ρ.
may be shown for the same set of K, τ, and ρ.  | Figure 1. Time response of x1 and estimate of a with respect to ρ |
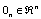 is a zero vector and
is a zero vector and 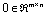 is a zero matrix with appropriate dimensions.
is a zero matrix with appropriate dimensions. 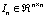 is a square identity matrix and
is a square identity matrix and 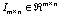 is an identity matrix in the sense that all diagonal elements are one whatever the dimension of the matrix is. If
is an identity matrix in the sense that all diagonal elements are one whatever the dimension of the matrix is. If 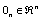 is a vector, diag(x) is a diagonal matrix with the vector x forming the diagonal and diag(x,i) (or diag(x,-i)) is a square matrix of size (n+i) with the vector x forming the i th super-diagonal (or sub-diagonal) stands for a positive definite (or semidefinite) matrix, Tr(X) is the sum of all diagonal entries in X.
is a vector, diag(x) is a diagonal matrix with the vector x forming the diagonal and diag(x,i) (or diag(x,-i)) is a square matrix of size (n+i) with the vector x forming the i th super-diagonal (or sub-diagonal) stands for a positive definite (or semidefinite) matrix, Tr(X) is the sum of all diagonal entries in X.2. Problem Statement
- Consider the class of nonlinear system as follows:
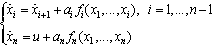 | (6) |
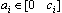 , fi and
, fi and 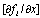 are continuous on
are continuous on 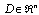 and
and 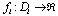 on
on 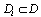 is a known nonlinear function in strict-feedback form in the sense that the fi depend only on
is a known nonlinear function in strict-feedback form in the sense that the fi depend only on 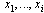 . It is implied that fi is locally Lipschitz and
. It is implied that fi is locally Lipschitz and 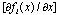 is bounded on Di[11]. Therefore, there exists a constant
is bounded on Di[11]. Therefore, there exists a constant 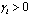 such that
such that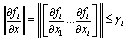 | (7) |
3. Adaptive Dynamic Surface Control
3.1. Design Procedure
- An outline of the standard design procedure for the adaptive DSC described in[6, 12] is as follows: Define the i th error surface as
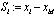 for
for 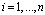 where x1d is the constant value. After taking the time derivative of Si along the trajectories of (6),
where x1d is the constant value. After taking the time derivative of Si along the trajectories of (6),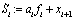 The surface error Si will converge to zero if
The surface error Si will converge to zero if 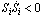 , however there is no direct control over the surface dynamics. If xi+1 is considered as the forcing term for the error surface dynamics, then the sliding condition outside some boundary layer is satisfied if
, however there is no direct control over the surface dynamics. If xi+1 is considered as the forcing term for the error surface dynamics, then the sliding condition outside some boundary layer is satisfied if 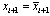 where
where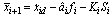 | (8) |
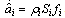 | (9) |
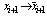 , so define
, so define 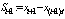 where
where 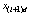 equals
equals 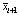 passed through a first-order filter,
passed through a first-order filter,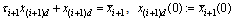 | (10) |
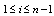 , define
, define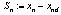 . After taking its derivative, the control input is
. After taking its derivative, the control input is 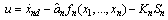 | (11) |
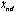 is calculated from (10) and the update law of
is calculated from (10) and the update law of 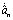 is following
is following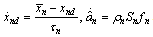 .
.3.2. Augmented Error Dynamics
- The augmented closed loop error dynamics is derived for analysis of stability and parameter convergence. After subtracting and adding
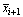 and
and 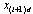 , and using u in (11), the closed-loop dynamics in (6) can be written as
, and using u in (11), the closed-loop dynamics in (6) can be written as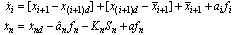 for
for 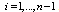 . Using (8) and the definition of error surfaces, the above equations can be described as a function of errors as follows:
. Using (8) and the definition of error surfaces, the above equations can be described as a function of errors as follows: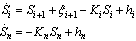 | (12) |
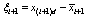 is the filter error and
is the filter error and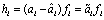 is the parameter estimation error multiplied by fi.In addition, we need to consider the augmented error dynamics due to inclusion of a set of the first order low pass filters and the update law for the estimate. After taking a derivative of
is the parameter estimation error multiplied by fi.In addition, we need to consider the augmented error dynamics due to inclusion of a set of the first order low pass filters and the update law for the estimate. After taking a derivative of 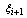 for
for  , the filter error dynamics is
, the filter error dynamics is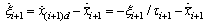 | (13) |
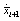 as
as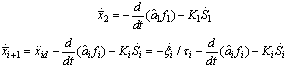 | (14) |
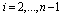 . Since the derivative of hi is written as
. Since the derivative of hi is written as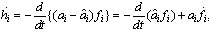 | (15) |
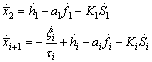 | (16) |
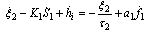 | (17) |
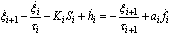 for
for 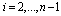 Equation (15) with the update law in (9) is written as
Equation (15) with the update law in (9) is written as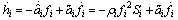 | (18) |
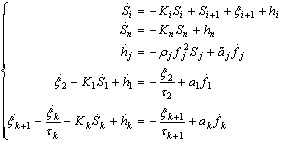 | (19) |
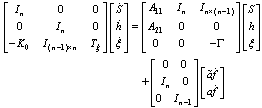 | (20) |
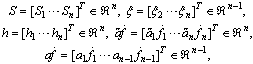 and the submatrices are
and the submatrices are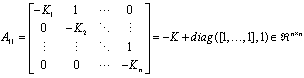
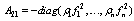
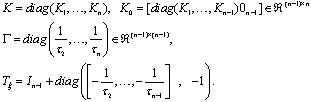 Since the first block matrix in (20) is invertible such that
Since the first block matrix in (20) is invertible such that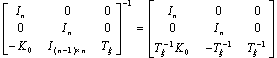 where
where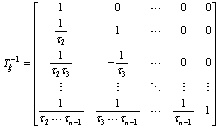 after multiplying the inverse matrix to both sides in (20), the augmented closed-loop error dynamics are written as
after multiplying the inverse matrix to both sides in (20), the augmented closed-loop error dynamics are written as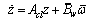 | (21) |
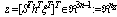 ,
,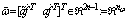 and the matrices are
and the matrices are where the submatrices are
where the submatrices are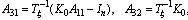
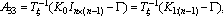
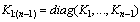 It is noted that the third row of
It is noted that the third row of 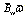 is
is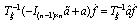 By defining
By defining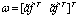 , (21) is rewritten as follows:
, (21) is rewritten as follows: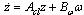 | (22) |
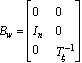 Next, we need to determine the upper bound of ω in (22). Using the assumption in (7), the upper bound of
Next, we need to determine the upper bound of ω in (22). Using the assumption in (7), the upper bound of 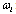 for
for 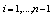 is
is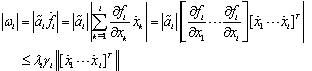
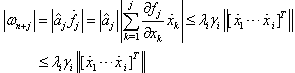 for j = 1,…,n-1. Using (12),
for j = 1,…,n-1. Using (12), 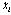 is written in a function of z as follows:
is written in a function of z as follows: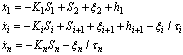 for
for  Therefore, there exists a matrix
Therefore, there exists a matrix 
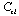
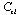 such that
such that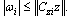 | (23) |
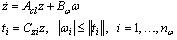 | (24) |
3.3. Quadratic Stability
- Since Acl in (24) is not time invariant due to A21 is (21), both A21 and A31 can be decomposed into a steady-state term and a time varying term under the assumption that
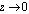 as
as 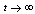 for the given set of controller gains. That is,
for the given set of controller gains. That is,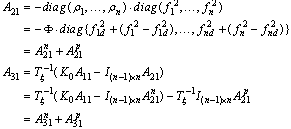 where
where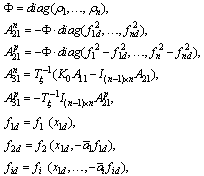 and
and 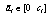 is a nominal constant, e.g.,
is a nominal constant, e.g., 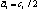 or a rough estimate of ai. Therefore, Acl can be written as
or a rough estimate of ai. Therefore, Acl can be written as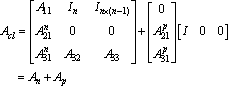 | (25) |
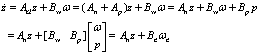 | (26) |
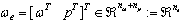
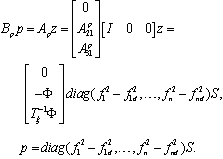 Since p is a function of S and is bounded on D, there exists a matrix Czi such that
Since p is a function of S and is bounded on D, there exists a matrix Czi such that 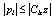 for i = 2,…,n-1.
for i = 2,…,n-1.Finally, the augmented error dynamics in (24) can be written as
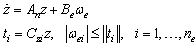 | (27) |
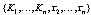 , and update law gains,
, and update law gains,  . The augmented error dynamics in (27) is quadratically stable if there exists a positive definite matrix p such that
. The augmented error dynamics in (27) is quadratically stable if there exists a positive definite matrix p such that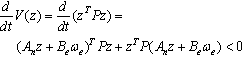 | (28) |
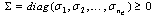 such that
such that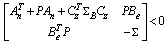 | (29) |
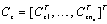 ,
, 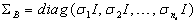 is the diagonal block matrix. The equivalence between (28) and (29) can be referred to[13].Remark 1. If there exists the solution for (29), z = 0 is exponentially stable. That is, x1→x1d and
is the diagonal block matrix. The equivalence between (28) and (29) can be referred to[13].Remark 1. If there exists the solution for (29), z = 0 is exponentially stable. That is, x1→x1d and 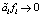 as t→∞. Moreover, if fi satisfies the so called “persistent excitation”[6], i.e., there exist strictly positive constants ai and T such that for any t > 0,
as t→∞. Moreover, if fi satisfies the so called “persistent excitation”[6], i.e., there exist strictly positive constants ai and T such that for any t > 0,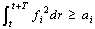
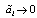 as t→∞. Otherwise, it is not guaranteed for the estimated parameter to converge to the correct value although x1→x1d as t→∞.
as t→∞. Otherwise, it is not guaranteed for the estimated parameter to converge to the correct value although x1→x1d as t→∞.4. Illustrative Example
- Consider (1) again with the unknown parameter a = 1 and the control objective is x1→x1d = 1. Suppose the domain
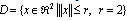 and
and 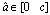 where c = 2. Then,
where c = 2. Then,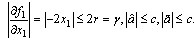 If the controller derived in Section 1 is applied, the closed-loop error dynamics is following as in (19):
If the controller derived in Section 1 is applied, the closed-loop error dynamics is following as in (19):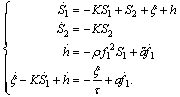 | (30) |
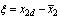 and
and 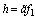 . Equation (30) can be written in matrix form as follows:
. Equation (30) can be written in matrix form as follows: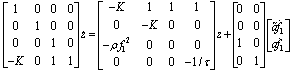 | (31) |
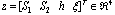 . As derived in (22), (31) can be writtens as
. As derived in (22), (31) can be writtens as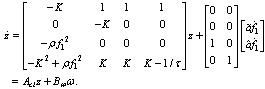 where
where 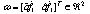 and the upper bound of w is determined as follows:
and the upper bound of w is determined as follows: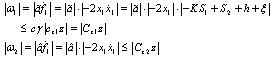 where
where 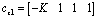 and
and 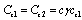 Therefore, the augmented error dynamics can be written in LDI form as
Therefore, the augmented error dynamics can be written in LDI form as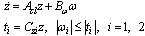 | (32) |
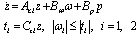 | (33) |
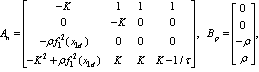
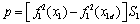 is a vanishing perturbation and its upper bound is
is a vanishing perturbation and its upper bound is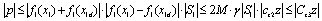 where m is a maximum of f1 on D, i.e.,
where m is a maximum of f1 on D, i.e., 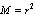 ,
,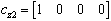 and
and 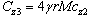 . Finally, the augmented error dynamics is written in diagonal norm-bouned LDI as
. Finally, the augmented error dynamics is written in diagonal norm-bouned LDI as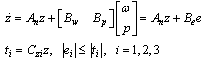 | (34) |
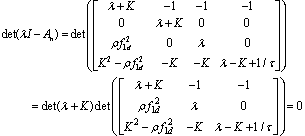 where
where 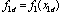 . Then,
. Then,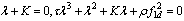 It is noted that the decond characteristic equation can be derived using Symbolic Math Toolbox of MATLAB. Using the Routh stability criterion, the inequality condition for An to be Hurwitz is derived to be
It is noted that the decond characteristic equation can be derived using Symbolic Math Toolbox of MATLAB. Using the Routh stability criterion, the inequality condition for An to be Hurwitz is derived to be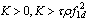 | (35) |
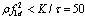 If three values of ρare considered, i.e., ρi={1,10,70}, i = 1,2,3, three ranges of x1d for An to be Hurwitz are obtained as follows:
If three values of ρare considered, i.e., ρi={1,10,70}, i = 1,2,3, three ranges of x1d for An to be Hurwitz are obtained as follows: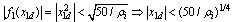 | (36) |
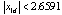 for ρ1 = 1,
for ρ1 = 1, 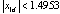 for ρ2 = 10 and
for ρ2 = 10 and 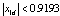 for ρ3 = 70. When x1d = 1 and ρi is either 1 or 10, the matrix An in (32) is Hurwitz for both cases and LMI (29) can be solved via convex optimethod called CVX[14] is used to solve the feasibility problem by calculating P and Σ in (29) numerically in the framework of MATLAB. As predicted through stability analysis, x1→x1d and
for ρ3 = 70. When x1d = 1 and ρi is either 1 or 10, the matrix An in (32) is Hurwitz for both cases and LMI (29) can be solved via convex optimethod called CVX[14] is used to solve the feasibility problem by calculating P and Σ in (29) numerically in the framework of MATLAB. As predicted through stability analysis, x1→x1d and 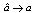 as t→∞ as shown in Fig. 1. For ρ3 = 70, the eigenvalues of An are
as t→∞ as shown in Fig. 1. For ρ3 = 70, the eigenvalues of An are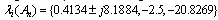 Since the matrix An is not Hurwitz, this results in the oscillatory estimate of a and thus oscillatory tracking of
Since the matrix An is not Hurwitz, this results in the oscillatory estimate of a and thus oscillatory tracking of 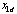 (refer to Fig 1).If x1d is changed to 1.5, the eigenvalues of An with respect to ρi are
(refer to Fig 1).If x1d is changed to 1.5, the eigenvalues of An with respect to ρi are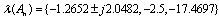 for
for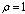 ,
,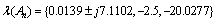 for
for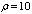 .It is shown in Fig. 2 that the time responses of for x1 and
.It is shown in Fig. 2 that the time responses of for x1 and 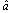 are oscillatory for ρ2 while the tracking error and parameter estimation error converges to zero for ρ1. If τ becomes smaller as 0.01, the inequality condition in (36) is modified as
are oscillatory for ρ2 while the tracking error and parameter estimation error converges to zero for ρ1. If τ becomes smaller as 0.01, the inequality condition in (36) is modified as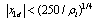 | (37) |
 are shown in Fig. 3. It is remarked that a smaller gain of τ allows us to enlarge the range of x1d for An to be Hurwitz. However, it is well known that 1/τ in the first-order filter is a cut-off frequency and the noise thus may not be attenuated if τ is too small.
are shown in Fig. 3. It is remarked that a smaller gain of τ allows us to enlarge the range of x1d for An to be Hurwitz. However, it is well known that 1/τ in the first-order filter is a cut-off frequency and the noise thus may not be attenuated if τ is too small.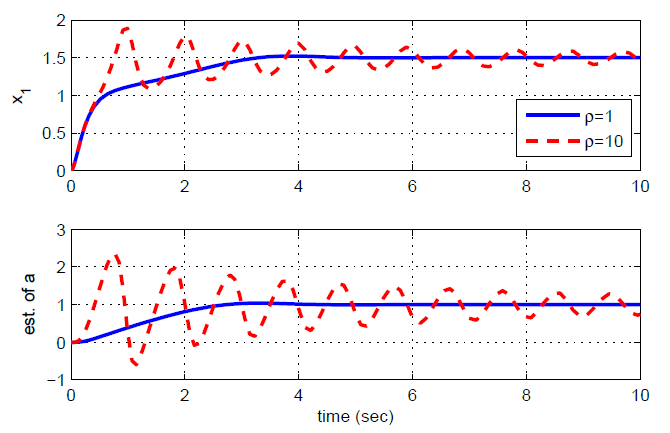 | Figure 2. Time response of x1 and  with respect to ρfor x1d =1.5 with respect to ρfor x1d =1.5 |
 | Figure 3. Time response of x1 and  with respect to ρfor with respect to ρfor |
5. Conclusions
- The analysis method for stability and parameter convergence of adaptive dynamic surface control was proposed by deriving the augmented closed-loop error dynamics in linear differential inclusion form. The sufficient condition for stability is derived for the given controller gains in the form of linear matrix inequality. It allows us to analyze both quadratic stability and parameter convergence by computing a quadratic Lyapunov function numerically via convex optimization.
ACKNOWLEDGEMENTS
- This research was supported by the Industrial Strategic Technology Development Program (10035250, Development of Spatial Awareness and Autonomous Driving Technology for Automatic Valet Parking) funded by the Ministry of Knowledge Economy (MKE, Korea).
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML