1. Introduction

The designs of adaptive controllers forparametricun-certain linear or non-linear systems have become one of the most researched topics in control theory for the past two decades. Most of the parametric adaptive control scheme involves a very complex mathematical derivation[1-3]. Thus, the design process becomes difficult and almost impossible for a high order plant. The approaches will directly or indirectly identify the system model and based on this model, a fixed structure adaptive controller will be derived. Then, the parameters of the model and the controller will be updated recursively at every sampling time.

Adaptive control involves modifying the controllerparameters so that it can cope with the fact that the parameters of the system being controlled are slowly time-varying or uncertain. Adaptive laws have been used to update the controller parameters in order to achieve the desired system performance in the sense of closed-loop stability and output tracking of a desired reference output[4-5]. The ability toautomatically adapt to variations in plant dynamics andenvironment has made adaptive controllers become increasingly important for various applications. However, mathematical modelling of the plant has to be done, before they can be implemented, which sometimes is complicated and difficult. In addition, inaccurate model of the plant could lead on degraded performances of the adaptive controllers.

Lately, adaptive neural networks (ANN) have beenstudied and applied in various disciplines such as engineering, economics, cognitive science, computer, biomedical, etc. The ANN approach has a high potential for identification and control applications mainly because it can approximate the nonlinear input-output mapping of a dynamic system[6]. As a result, numerous adaptive neuro-control techniques have been proposed to replace the conventional classical methods[7]. The advantage of neuro-control techniques is that they can provide a ‘black box’ controller which can be re-trained for other applications. It is also can adapt to change in uncertain conditions; and provide ‘soft’ failure characteristics and nonlinear control laws[8].

Multi Layered Perceptron (MLP) is the most popular structure of ANN models and has a capability on general approximation of any continuous function[9]. However, the learning rate of MLP is quite slow if the MLP network is trained using back propagation algorithm, which is based on a gradient descent technique. Mehrabian[10] proposed a model reference adaptive neuro-control using feed-forward neural network with momentum back-propagation (MBP) learning algorithm. This controller has been utilized to control a nonlinear system. However, it needs some tuning of parameters that require a few trails and error to be properly selected.

To overcome this problem, MLP network with linear connection, called the Hybrid Multi Layered Perceptron (HMLP) network has been introduced and proven to have better performance as compared to the standard MLP network[11]. A few performance comparisons also have been made between ANC based on HMLP network and other controllers. The results show that the ANC gave significant improvement in the performance of controlling unstable system[12-14].

Thus, in this paper, the ANC based on HMLP network has been proposed to control the dynamics system. The Recursive Least Square algorithm which is based on Gauss-Newton technique is combined with HMLP network to improve the time response and tracking performance in various operating conditions such as noise, varying gain and disturbance torques. The performances of the proposed controller is compared with ANC based on standard MLP network and Adaptive Parametric Black Box (APBB) controller.

2. Controller Structure

In this paper, Model Reference Adaptive System (MRAS) has been chosen as the control scheme for ANCs and APBB controllers as shown in Figure 1. The control scheme will estimate controller parameters directly. For estimating the controller parameters instead of model parameters, some modifications are required[15]. For a given reference input, a reference model is used to produce the desired output.

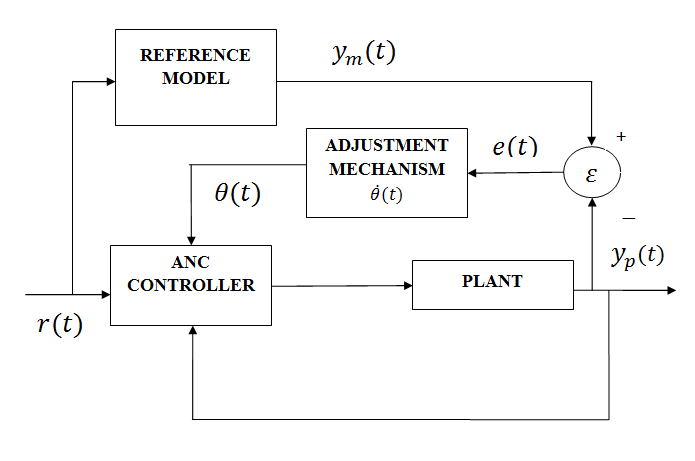Figure 1. Block diagram of a model reference adaptive system

The equation for reference model is given by:

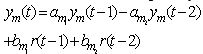(1)

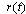where is reference input and 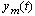is reference model output. The objective of parameter adjustment is to adjust the error between the plant output and the output from reference model. The model following error is defined by:

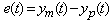(2)

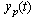where is the plant output.

3. Methodology

3.1. Hybrid Multi Layered Perceptron (HMLP) Networks

Cybenko[6] and Funahashi[16] proved that the Multi Layered Perceptron (MLP) network with one hidden layer is sufficient to approximate any continuous function with reasonable accuracy. However, the training process of MLP takes a large computation time and often leads to local minima problem[8][17]. Normally, the MLP network consists of an input layer of source neurons, with at least one hidden layer of computational neurons, and an output layer of computational neurons[18-19]. The input layer acts as an input data holder that distributes the input to the first hidden layer. The outputs from the first hidden layer then become the inputs to the second layer and so on. The last layer acts as the network output layer. For HMLP network, the additional linear inputs are connected directly to the output nodes via some weighted connections to form a linear model in parallel with the nonlinear original MLP model. These additional linear input connections do not significantly increase the complexity of the MLP network since the connections are linear. HMLP networks are feed forward neural networks with one or more hidden layers. A model of HMLP network with one hidden layer is shown in Figure 2.

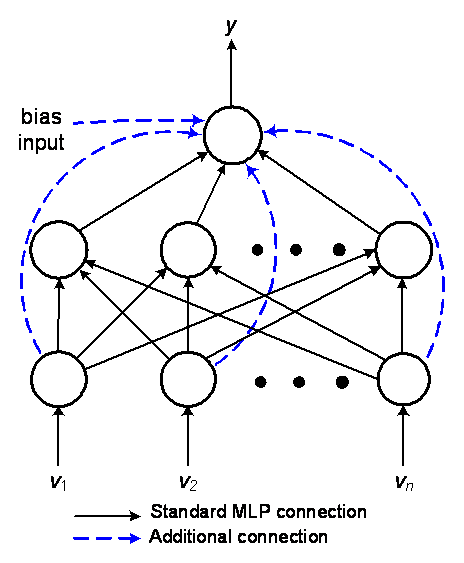Figure 2. Hybrid Multi Layered Perceptron (HMLP) Network

In the current study, HMLP network with a single output node and a single hidden layer are used. With these simplifications, the network output becomes:

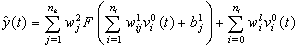(3)

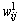where and 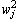denote as the weights in the first layer and the second layer; 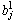and 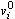on the other hand denote the thresholds in the hidden nodes and inputs that are supplied to the input layer. The numbers of input node and hidden node are represented by 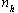and 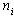respectively. 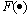is an activation function that is normally selected as a sigmoid function:

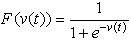(4)

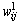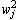The weight , and the threshold 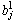are unknown and which will be adjusted by adjustment mechanism in order to minimize the prediction errors. the prediction error can define by the equation shown below:

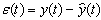(5)

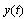where is the desired output and 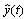is the actual network output.

3.2. Adaptive Parametric Black Box (APBB) Controller

The control scheme of the APBB controller is very similar to the control scheme of black box Artificial Intelligence (AI) controller. The adjustment mechanism is an on-line least square (LS) family algorithm. Instead of estimating the model of the plant as in conventional parametric adaptive controller approach, the algorithm will be used to update or estimate the controller parameters directly. The controller parameters will be adjusted to minimize the errors occur between the plant output and the reference input.

The controller structure is an ARMAX model of a suitable order. However, a low order controller is preferable for fast and effective parameters update. A second order controller structure is given below[15]:

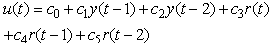(6)

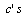where are the controller parameters that need to be adjusted to minimize the cost function.

3.3. Estimation Algorithm

In this paper, all controller parameters have been estimated using Recursive Least Square (RLS) as an estimation algorithm in order to reduce the cost function. The RLS algorithm has been used extensively in adaptive filtering, self-tuning control, system identification and prediction, and interference cancellation[20]. In neural network applications, Azimi-Sadjadi and Liou[21] had introduced the RLS algorithm with constant forgetting factor as training algorithm for MLP network.

The convergence rate of the ANC controllers is further improved by proposing a modified version of the RLS called Weighted Recursive Least Square (WRLS) algorithm which also known as Exponential Forgetting Factor. This modification to RLS algorithm is require such that the additional weights of the neural network can be estimated. Exponential forgetting factor is a way to discard old data. It is based on the assumption that the least-squares loss function is replaced in with an old data that is discounted exponentially.

For all, given and set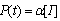, the WRLS estimate 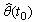using the following recursive equations[1]:

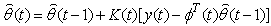(7)

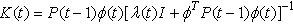(8)

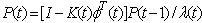(9)

Mashor[15] modified Equation (7) according to:

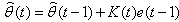(10)

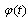where e is the difference between plant output and reference input. The information vector that consists of the controller inputs is represented by while 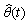represent the vector of controller parameters. Other symbols are defined and assigned according to the standard WRLS algorithm[1]. Another modification that is required to speed up the learning process is by resetting the covariant matrix 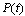and forgetting factor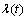, if the model following error becomes significantly large. The resetting is based on the following equation:

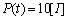(11)

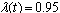(12)

4. Results and Discussions

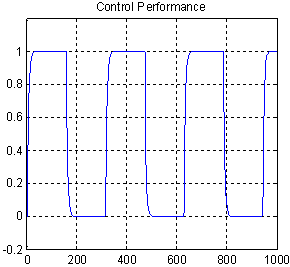Figure 3. Output Response for Model Reference

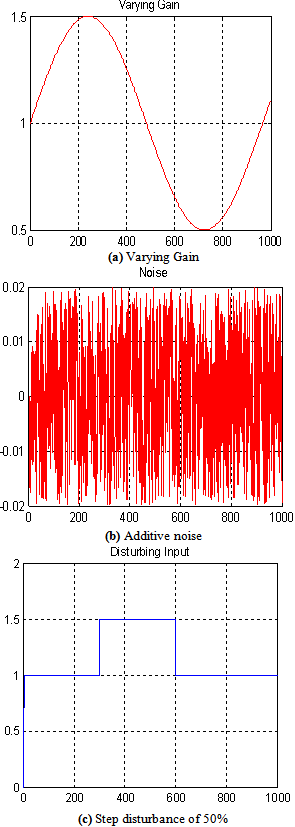Figure 4. Varying operating conditions

For this comparison, the simulated plants can be described by a difference equation in a form shown below:

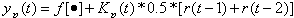(13)

The specific plant used in the simulation study was[22]:

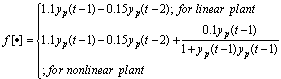(14)

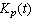where is a varying gain, the inputis 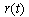is the uniformly bounded reference input. 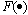is a simulated plant that consist of linear or nonlinear plant. Model reference was selected as:

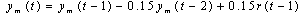(15)

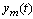where is a reference model output. Parameter 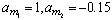and 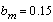have been chosen such that a desired trajectory 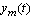is obtained for the plant output 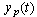to follow.

The cost functions for model following was set to:

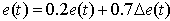(16)

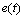where is a proportional error and 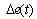is a differential error.

In this section, the simulation results of linear and nonlinear plant using the models suggested earlier will be presented. Figure 3 shows the output response of the model reference. The simulation results for the controllers using the same operating conditions such as varying gain, noise (white noise with zero mean and variance 0.0131) and 50% step disturbance are shown in Figure 4.

4.1. Linear Plant

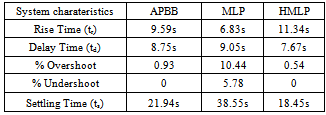
The simulation results for linear plant are given in Figure 5 to Figure 9. The varying operating conditions such as varying gain, noise and disturbance that have been applied are shown in Figure 7, 8 and 9, respectively. The time response of the system for ANCs and APBB controllers are shown in Figure 5, while Figure 6 shows the output response with square wave input. In Figure 5, it shows that the output response start at 5s due to the initial condition state. The numerical analysis for time response of ANCs and APBB controllers can be referred in Table 1. For settling time calculation, the error band that was used in this analysis is 2%. Delay time will be taken when the response reach half the final value for the very first time. By referring to Figure 5 and 6, the output response for unity gain shows that all controllers can smoothly track the model reference. It is also indicates that HMLP controller produces better results, where the percentage of overshoot, settling time, delay time and percentage of undershoot is significantly less compared to the MLP and APBB controller. Only in terms of rise time, the MLP and APBB controller produced a better rise time but having a large delays response of 9.1s for MLP and 8.8s for APBB controllers.

Table 1. Performance Comparison between ANC and PID Controllers for Linear Plant

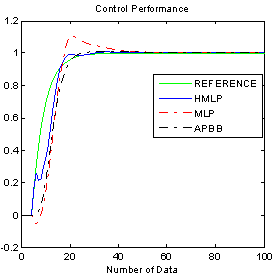Figure 5. Step response of ANC and APBB controllers for unity gain

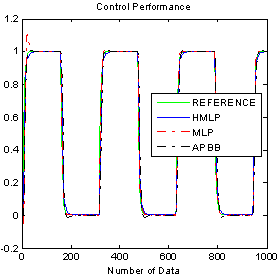Figure 6. Comparison result with unity gain

Figure 7 shows the output response of all controllers for the plant with varying gain. The output response of HMLP controller follow the desired response at the high gain and still able to track the desired response smoothly at the low gain. Meanwhile, the response of MLP controller degrades with high overshoot especially at the low gain. Figure 8 shows the system is subjected to measurement noise. All the controllers still able to track the reference model response very well despite the significant noise.

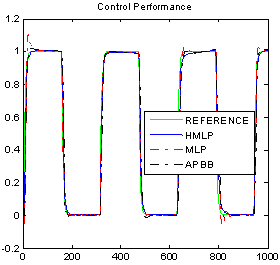Figure 7. Comparison result with varying gain

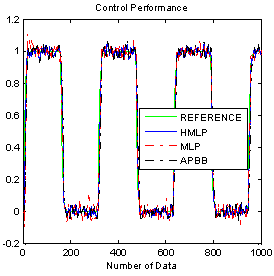Figure 8. Comparison result with additive noise

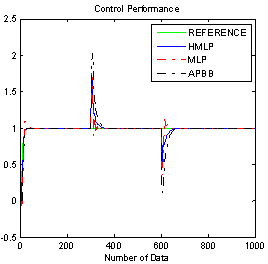Figure 9. Comparison result with step disturbance

Figure 9 shows the response of the system when a step disturbance with strength of 50% was introduced between 300s and 600s. Output response from ANCs controllers only reaches 60% overshoot in response to the disturbance while APBB controller output almost reach 100%. The figure also shows that output response for HMLP controllers settle to a steady state rapidly when the plant encounter disturbances. It points out that the performance of HMLP controller is significantly better than MLP and APBB controller when dealing with disturbance.

4.2. Nonlinear Plant

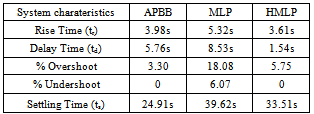
The simulation results for non linear plant by applying the same varying gain, noise and disturbance that have been used in Figure 4 are shown in Figure 10 to Figure 14. The time response of the system with ANCs and APBB controllers are shown in Figure 10, while Figure 11 shows the output response with square wave input. The numerical analysis for time response of ANCs and APBB controller can be referred to Table 2. The analysis indicates that the HMLP controller produces better result where its rise time, delay time and percentage of undershoot is significantly less as compared to the MLP and APBB controllers. As of settling time and percentage of overshoot, APBB overrun MLP by providing better result where the output response has longer settling time. On the other hand, output response of MLP controller has a longer settling time along with 18% of percentage of overshoot. To put in a nut shell, HMLP controller is able to provide a faster response with a small delay and undershoot.

Table 2. Performance Comparison between ANC and PID Controllers for Nonlinear Plant

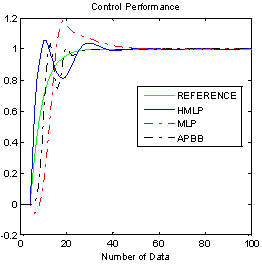Figure 10. Step response of ANC and APBB controllers for unity gain

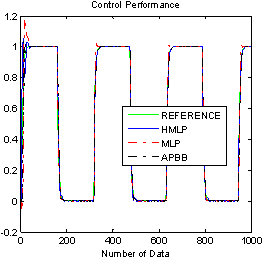Figure 11. Comparison result with unity gain

Figure 12 shows all controllers can still control the system with 50% varying gain but degradation was shown by MLP at low gain while HMLP and APBB on the other hand present better response. Figure 13 shows the system is subjected to measurement noise known as Gaussian white noise sequence with zero mean and variance of 0.0131. The plot shows that the HMLP controller can produce good result, while output response of MLP degraded with high oscillations. It can also be observed that the simulation results for all controllers are capable to follow the reference output and remain stable under measurement noise.

Figure 14 shows the response of the system when a step disturbance with strength 5% has been introduced between 300s and 600s. Output response from HMLP controller is better than the output response from the MLP and APBB controllers due to its ability to converge in a shorter time after disturbance. Figure 14 shows that output response for HMLP and APBB controller reach 50% overshoot at the beginning of the disturbance while MLP controller almost reaches 100% of overshoot.

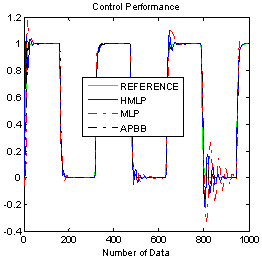Figure 12. Comparison result with varying gain

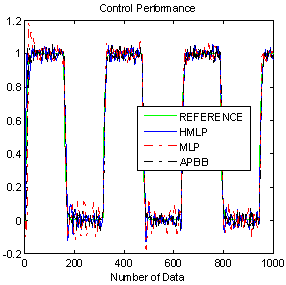Figure 13. Comparison result with additive noise

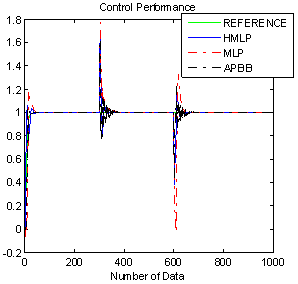Figure 14. Comparison result with step disturbance

5. Conclusions

An Adaptive Neuro-Controller based on Hybrid Multi Layered Perceptron network for the purpose of controlling dynamics system have been presented The controller structure is a direct type and can employ the feed forward neural network to compensate adaptively with various parameters in the plant, disturbance torque and varying operating conditions. The performance of proposed controller has been evaluated based on the capability of the controlled output to track the reference output and in terms of time response analysis. The performance of ANC based on HMLP controller has been compared with ANC based on standard MLP network and APBB controller. Here, the simulated data has been used for the comparison. Based on Table 1 and 2, it can be observed that the performance of the HMLP controller is better than the MLP and APBB controllers in terms of percentage of overshoot, percentage of undershoot, delay time and settling time. From the output response for linear and nonlinear plant, it points out that performance of ANC based on HMLP network is significantly better than ANC based on MLP network and APBB controller. Based on the simulation results and performance analysis for all controllers, it can be clarify that the AN based on HMLP network is sufficient to control the plants under unpredictable and dynamics conditions. It is also observed that ANC based on HMLP network has better tracking performance compared to the MLP and APBB controllers for linear and nonlinear plant.

ACKNOWLEDGEMENTS

The authors would like to thank Astronautic Technology (M) Sdn. Bhd., Malaysia for providing some information and advices for this work. We also gratefully acknowledge and thank the Ministry of Higher Education (MOHE) and University Malaysia Perlis (UniMAP) for providing the financial support under Fundamental Research Grant Scheme (FRGS) and Short-term Grant.