-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
2012; 2(3): 19-25
doi: 10.5923/j.control.20120203.01
Indirect Field Oriented Control of an Induction Motor Sensing DC-link Current with PI Controller
Rami A. Maher1, Walid Emar1, Mahmoud Awad2
1Electrical Engineering Dept., University of Al-Isra, Amman, 11622, Jordan
2Electrical Engineering Dept., Balqa University, Amman, 11134, Jordan
Correspondence to: Walid Emar, Electrical Engineering Dept., University of Al-Isra, Amman, 11622, Jordan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
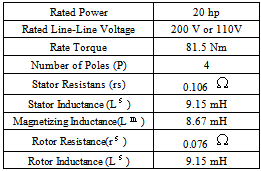
This paper describes an analysis method for achieving control torque and speed with indirect field oriented control for induction motors. An indirect field-oriented output feedback motor PI controller is presented; it is suitable for low-cost applications. A current model control is used to sense back electromotive force (back-EMF) by means of an analog to digital converter; its simulation and filtering are discussed. A Current model is the core of this work, but other system modules are analyzed such the proportional-integrative (PI) controller, the indirect field control with pulse width modulation and others. The paper also shows that PI controller is not an intelligent controller nor is the slip calculation accurate. Therefore, changes in rotor time constant degrade the speed performance. Another main problem in variable speed ac drives is the difficulty of processing feedback signal of the outer loop in the presence of harmonics.
Keywords: Induction Motor, Field Orientation, Indirect Field Control Method, PI Controller, Detuning Effect, Mechanical Loads, Torque Speed Characteristic, Load Characteristics
Article Outline
1. Introduction
- The fundamentals of vector control implementation can be explained with the help of Figure 1, where the machine model is presented in a synchronous rotating reference frame. The inverter is omitted from the figure, assuming that it has unity current gain, that is, it generates currents
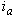 ,
, 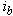 , and
, and 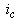 as dictated by the corresponding command currents
as dictated by the corresponding command currents 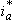 ,
, 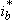 , and
, and 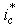 from the controller. A machine model with internal conversions is shown on the right. The machine terminal phase currents
from the controller. A machine model with internal conversions is shown on the right. The machine terminal phase currents 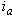 ,
, 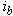 , and
, and 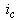 are converted to
are converted to 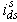 and
and 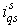 components by
components by 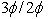 transformation. These are then converted to synchronously rotating frame by the unit vector components
transformation. These are then converted to synchronously rotating frame by the unit vector components 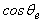 and
and 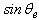 before applying them to the
before applying them to the 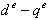 machine model. The controller makes two stages of inverse transformation, as shown, so that the control currents
machine model. The controller makes two stages of inverse transformation, as shown, so that the control currents 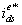 and
and 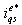 correspond to the machine currents
correspond to the machine currents 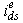 and
and 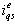 , respectively. In addition, the unit vector assures correct alignment of
, respectively. In addition, the unit vector assures correct alignment of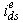 with the
with the 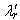 and
and 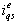 perpendicular to it, as shown.The transformation and inverse transformation including the inverter ideally do not incorporate any dynamics and therefore, the response to
perpendicular to it, as shown.The transformation and inverse transformation including the inverter ideally do not incorporate any dynamics and therefore, the response to 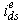 and
and 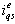 is instantaneous (neglecting computational and sampling delays).
is instantaneous (neglecting computational and sampling delays).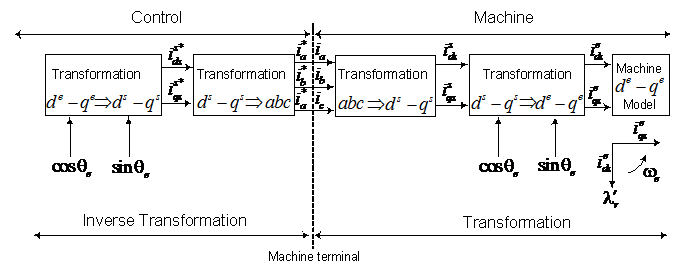 | Figure 1. Vector control implementation principle with machine dq model |
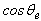 and
and 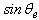 ) is generated for the control. It should be mentioned that the orientation of
) is generated for the control. It should be mentioned that the orientation of 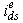 with the rotor flux
with the rotor flux 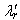 , air gap flux, or stator flux is possible in vector control. However, rotor flux orientation gives natural decoupling control, whereas air gap or stator flux orientation gives a coupling effect which has to be compensated by a decoupling compensation current [1,2].
, air gap flux, or stator flux is possible in vector control. However, rotor flux orientation gives natural decoupling control, whereas air gap or stator flux orientation gives a coupling effect which has to be compensated by a decoupling compensation current [1,2].2. Indirect Field Oriented Control
- Indirect vector control is very popular in industrial applications. Figure 2 explains the fundamental principle of indirect vector control with the help of a phasor diagram. The
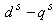 axes are fixed on the stator, but the
axes are fixed on the stator, but the 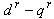 axes, which are fixed on the rotor, are moving at speed
axes, which are fixed on the rotor, are moving at speed 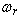 . Synchronously rotating axes
. Synchronously rotating axes 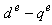 are rotating ahead of the
are rotating ahead of the 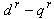 axes by the positive slip angle
axes by the positive slip angle 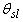 corresponding to slip frequency
corresponding to slip frequency 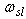 . Since the rotor pole is directed on the
. Since the rotor pole is directed on the 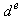 axis and
axis and 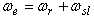 , one can write
, one can write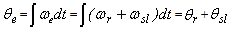 | (1) |
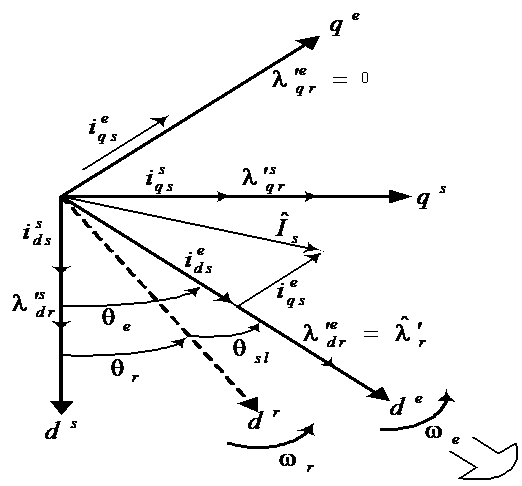 | Figure 2. Phasor diagram explaining indirect vector control |
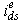 should be aligned on the
should be aligned on the 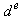 axis, and the torque component of current
axis, and the torque component of current 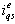 should be on the
should be on the 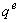 axis, as shown.For decoupling control, one can make a derivation of control equations of indirect vector control with the help of
axis, as shown.For decoupling control, one can make a derivation of control equations of indirect vector control with the help of 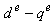 dynamic model of induction machine (IM) [1,2,3,4],
dynamic model of induction machine (IM) [1,2,3,4],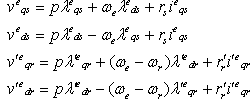 | (2) |
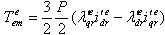 | (3) |
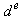 -axis is aligned with the rotor field, the q-component of the rotor field,
-axis is aligned with the rotor field, the q-component of the rotor field, 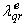 , in the chosen reference frame would be zero [1,2,5,6],
, in the chosen reference frame would be zero [1,2,5,6],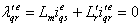 | (4) |
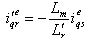 | (5) |
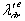 zero, the equation of the developed torque, Eq.(3), reduces to
zero, the equation of the developed torque, Eq.(3), reduces to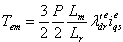 | (6) |
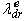 is not disturbed, the torque can be independently controlled by adjusting the stator q component current,
is not disturbed, the torque can be independently controlled by adjusting the stator q component current, 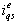 .For
.For 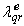 to remain unchanged at zero, its time derivative (
to remain unchanged at zero, its time derivative (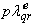 ) must be zero, one can show from Eq.(2) [6,1,2]
) must be zero, one can show from Eq.(2) [6,1,2]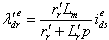 | (7) |
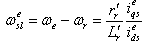 | (8) |
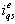 and slip speed
and slip speed 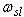 . Given some desired level of rotor flux,
. Given some desired level of rotor flux, 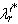 , the desired value of
, the desired value of 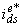 may be obtained from,
may be obtained from,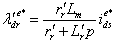 | (9) |
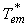 at the given level of rotor flux, the desired value of
at the given level of rotor flux, the desired value of 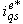 in accordance with Eq.(6) is
in accordance with Eq.(6) is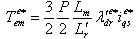 | (10) |
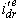 is zero,
is zero, 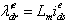 : thus, the slip speed of Eq.(8) can be written as
: thus, the slip speed of Eq.(8) can be written as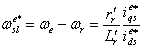 | (11) |
3. Indirect Field Orientation Detuning
- The success of FOC is based on the proper division of stator current into two components. Using the above d-q axis orientation approach, these two currents components are
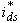 and
and 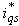 , which specify the magnetizing flux and torque respectively [1,2,4,10].The indirect FOC method uses a feedforward slip calculation to partition the stator current. The slip speed equation is rearranged as
, which specify the magnetizing flux and torque respectively [1,2,4,10].The indirect FOC method uses a feedforward slip calculation to partition the stator current. The slip speed equation is rearranged as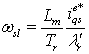 | (12) |
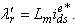 . The above condition, if satisfied, ensures the decoupling torque and flux production; a change in
. The above condition, if satisfied, ensures the decoupling torque and flux production; a change in 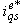 will not disturb the flux and the instantaneous torque control is achieved. This indicates that an ideal field orientation occurs. To what extent this decoupling is actually achieved will depend on the accuracy of motor parameters used. It is easy to be noted that the calculation of the slip frequency in Eq.(12) depends on the rotor resistance. Owing to saturation and heating, the rotor resistance changes and hence the slip frequency is either over or under estimated. Eventually, the rotor flux
will not disturb the flux and the instantaneous torque control is achieved. This indicates that an ideal field orientation occurs. To what extent this decoupling is actually achieved will depend on the accuracy of motor parameters used. It is easy to be noted that the calculation of the slip frequency in Eq.(12) depends on the rotor resistance. Owing to saturation and heating, the rotor resistance changes and hence the slip frequency is either over or under estimated. Eventually, the rotor flux 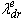 and the stator-axis current
and the stator-axis current 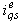 will be no longer decoupled in Eq.(10) and the instantaneous torque control is lost. Furthermore, the electromechanical torque generation is reduced at steady state under the plant parameter variations and hence the machine will work in a low-efficiency region. Finally, the variation of the parameters of moment of inertia J and the friction constant B is common in real applications. For instance, the bearing friction will change after the motor has run for a period of time [11]. Since the values of rotor resistance and magnetizing inductance are known to vary somewhat more than the other parameters, on-line parameter adaptive techniques are often employed to tune the value of these parameters used in an indirect field-oriented controller to ensure proper operation [2,11,12]. The detuning effect, generally, causes degradation in the drive performance.
will be no longer decoupled in Eq.(10) and the instantaneous torque control is lost. Furthermore, the electromechanical torque generation is reduced at steady state under the plant parameter variations and hence the machine will work in a low-efficiency region. Finally, the variation of the parameters of moment of inertia J and the friction constant B is common in real applications. For instance, the bearing friction will change after the motor has run for a period of time [11]. Since the values of rotor resistance and magnetizing inductance are known to vary somewhat more than the other parameters, on-line parameter adaptive techniques are often employed to tune the value of these parameters used in an indirect field-oriented controller to ensure proper operation [2,11,12]. The detuning effect, generally, causes degradation in the drive performance. 4. Simulation Results
4.1. Simulation of Fixed Voltage Open-Loop Operation
- The model equations of the IM, Eq.(2), in the stationary qd reference frame are modeled using SIMULINK [13,14]. The simulation is set up for simulating the dynamic behavior of the motor with fixed-step type. The results from these open-loop operations will later be used as a benchmark to compare the performance of the same motor operated with field-oriented control.In the model, three-phase voltages of base frequency (
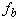 =50 Hz) applied to the input are converted into two-phase stationary reference frame voltages. Once d-q phase voltages obtained, the associated flux and current are calculated and then applied to electromechanical and mechanical torque equations to obtain torque-speed responses. One can see from Figure 3 the monotonic response of the magnetization current before it reaches its steady-sate value (about 82A) and how well the flux amplitude remains constant when the load torque is not constant.The value of the externally applied mechanical torque is generated by a repeating sequence source with the time and output values scheduled as shown in Figure 3.Sample results show that the electromechanical torque response of Figure 3 is smooth in case of IFOC, while it is oscillatory in open loop case shown in [1].
=50 Hz) applied to the input are converted into two-phase stationary reference frame voltages. Once d-q phase voltages obtained, the associated flux and current are calculated and then applied to electromechanical and mechanical torque equations to obtain torque-speed responses. One can see from Figure 3 the monotonic response of the magnetization current before it reaches its steady-sate value (about 82A) and how well the flux amplitude remains constant when the load torque is not constant.The value of the externally applied mechanical torque is generated by a repeating sequence source with the time and output values scheduled as shown in Figure 3.Sample results show that the electromechanical torque response of Figure 3 is smooth in case of IFOC, while it is oscillatory in open loop case shown in [1].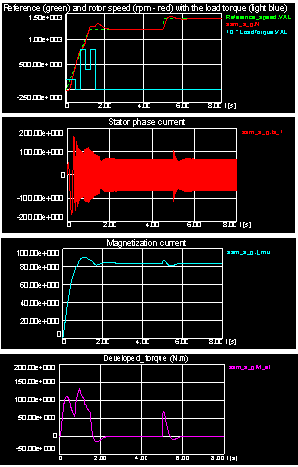 | Figure 3. Startup and load transients with field-oriented control |
4.2. Simulation of IFOC developed in Stationary Reference Frame and Frequency Converter
- This simulation is implemented to be familiar with indirect field-oriented control and to observe the variables at every stage of the control. The validity of IFOC technique is verified via two tests. In the first test, a change in stator quadrature current is generated by applying a variable value of the main inductance of the motor as shown in Figure 4a or as shown in Figure 4b by applying a repeating sequence source with the time and output values scheduled as follows:time_change_iqse= [ 0 0.6 0.8 0.9 2]output_change_iqse= [0 0 10 10 0 0]
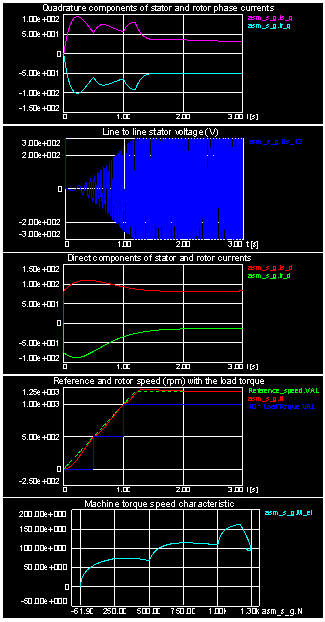 | Figure 4a. Changes in Responses due to a change in the magnetization current |
 | Figure 4b. Changes in Responses due to a change in quadrature current 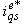 |
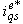 . The same change values are fed to the direct stator current in synchronous frame
. The same change values are fed to the direct stator current in synchronous frame 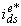 in the other test. The reflection of these changes on the output synchronous qd components of the stator currents,
in the other test. The reflection of these changes on the output synchronous qd components of the stator currents, 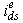 and
and 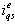 , and then to what extent the IFOC technique performs the decoupling action is investigated in Figures 4 and 5.
, and then to what extent the IFOC technique performs the decoupling action is investigated in Figures 4 and 5. | Figure 5. Changes in Responses due to change in 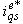 |
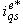 immediately appears at its corresponding output,
immediately appears at its corresponding output, 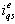 , while no change is detected in
, while no change is detected in 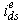 and rotor flux magnitude
and rotor flux magnitude 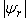 . Also, the figure shows the change in the response of developed torque and rotor speed due to this current changeIn Figure 5, the change in
. Also, the figure shows the change in the response of developed torque and rotor speed due to this current changeIn Figure 5, the change in 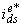 gives rise to a corresponding change in
gives rise to a corresponding change in 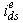 , which in turn affects the response of rotor flux magnitude
, which in turn affects the response of rotor flux magnitude 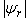 . No reflection of this change to
. No reflection of this change to 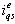 has been seen, and therefore, no change in the torque and speed responses would be expected. Thus, the observations seen in Figures 4 and 5 give a strong indication that the decoupling action is well performed by IFOC technique and the machine is, by now, a dc like machine. However, the conclusion that induction machine model has been converted to dc like machine is not yet decisive. There is still a problem behind the calculation of slip frequency, where the changes in rotor resistance could cause degradation in IFOC technique performance and the coupling effect might again be arisen.
has been seen, and therefore, no change in the torque and speed responses would be expected. Thus, the observations seen in Figures 4 and 5 give a strong indication that the decoupling action is well performed by IFOC technique and the machine is, by now, a dc like machine. However, the conclusion that induction machine model has been converted to dc like machine is not yet decisive. There is still a problem behind the calculation of slip frequency, where the changes in rotor resistance could cause degradation in IFOC technique performance and the coupling effect might again be arisen.4.3. Simulation of IFOC IM with Detuning Effect:
- The examination of detuning effect in the rotor resistance is performed by introducing an estimation factor,
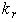 , to all the
, to all the 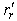 terms of machine model. As set up, perfect tuning is when
terms of machine model. As set up, perfect tuning is when 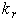 =1. The previous run of perfect tuning, Figure 3, is repeated at fixed reference speed (ramped up to speed
=1. The previous run of perfect tuning, Figure 3, is repeated at fixed reference speed (ramped up to speed 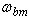 in 0.5 sec) for a
in 0.5 sec) for a 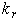 =1.5 and 0.5, with no-load, rated load and with cyclic change of load.Figures 6 and 7 are run with no-load and with estimation factors kr=0.5 and 1.5 respectively. It is evident from these figures that the speed responses are not much affected by this change in rotor resistance, where both responses reaches settling time at 0.5 sec. However, their steady state values never reaches the value of the reference value as in the case where kr=1. But, the dramatic changes are observed in the flux linkage levels and their time constants. The level of flux linkage in Figure 6 is higher than that in Figure 7, but the response time of Figure 6 is slower than for Figure 7; a valid justification, since the flux linkage time constant is inversely proportional to the rotor resistance value.The above run is repeated with rated load torque (Trated=81.49), and the responses of Figure 8 and Figure 9 will be obtained. The speed responses obtained from this test show a temporary jump at motor start-up. Moreover, the steady state speed errors resulting from this test are larger than that with no-load test; with kr=0.5, the speed settles at 189.64 rad/s , while it settles at 191 rad/s when kr=1.5. It is clear from the figures that the developed torque response with kr=1.5 is much distorted as compared to the smooth envelope in case kr=0.5. Also, the current waveform shows a larger swing when kr=1.5 as compared to waveform with kr=0.5. Finally, Figure 10 shows an oscillatory and low level flux linkage compared to the monotonic and higher level flux response in Figure 9, with kr=0.5. In the next study, the machine is subjected to the same sequence of step changes in load torque as previously applied in perfect tuning, Figure 4. As compared to the perfect tuning case, the increased value of rotor resistance (1.5
=1.5 and 0.5, with no-load, rated load and with cyclic change of load.Figures 6 and 7 are run with no-load and with estimation factors kr=0.5 and 1.5 respectively. It is evident from these figures that the speed responses are not much affected by this change in rotor resistance, where both responses reaches settling time at 0.5 sec. However, their steady state values never reaches the value of the reference value as in the case where kr=1. But, the dramatic changes are observed in the flux linkage levels and their time constants. The level of flux linkage in Figure 6 is higher than that in Figure 7, but the response time of Figure 6 is slower than for Figure 7; a valid justification, since the flux linkage time constant is inversely proportional to the rotor resistance value.The above run is repeated with rated load torque (Trated=81.49), and the responses of Figure 8 and Figure 9 will be obtained. The speed responses obtained from this test show a temporary jump at motor start-up. Moreover, the steady state speed errors resulting from this test are larger than that with no-load test; with kr=0.5, the speed settles at 189.64 rad/s , while it settles at 191 rad/s when kr=1.5. It is clear from the figures that the developed torque response with kr=1.5 is much distorted as compared to the smooth envelope in case kr=0.5. Also, the current waveform shows a larger swing when kr=1.5 as compared to waveform with kr=0.5. Finally, Figure 10 shows an oscillatory and low level flux linkage compared to the monotonic and higher level flux response in Figure 9, with kr=0.5. In the next study, the machine is subjected to the same sequence of step changes in load torque as previously applied in perfect tuning, Figure 4. As compared to the perfect tuning case, the increased value of rotor resistance (1.5 ) could cause the responses of flux linkages, torque and current to be distorted, especially, at time of load exertion, as shown in Figure 10. Also, at this time the speed deviation from its steady state value is larger than the case with kr=1. The situation with the decreased rotor resistance is shown in Figure 11. The responses of Figure 11 are run with kr=0.625; the minimum allowable value below which fluctuations will appear at the developed toque response at load exertion times. One can easily observe the amount of deviation in rotor flux linkage, speed and current responses as compared to the perfect tuning case.
) could cause the responses of flux linkages, torque and current to be distorted, especially, at time of load exertion, as shown in Figure 10. Also, at this time the speed deviation from its steady state value is larger than the case with kr=1. The situation with the decreased rotor resistance is shown in Figure 11. The responses of Figure 11 are run with kr=0.625; the minimum allowable value below which fluctuations will appear at the developed toque response at load exertion times. One can easily observe the amount of deviation in rotor flux linkage, speed and current responses as compared to the perfect tuning case.
|
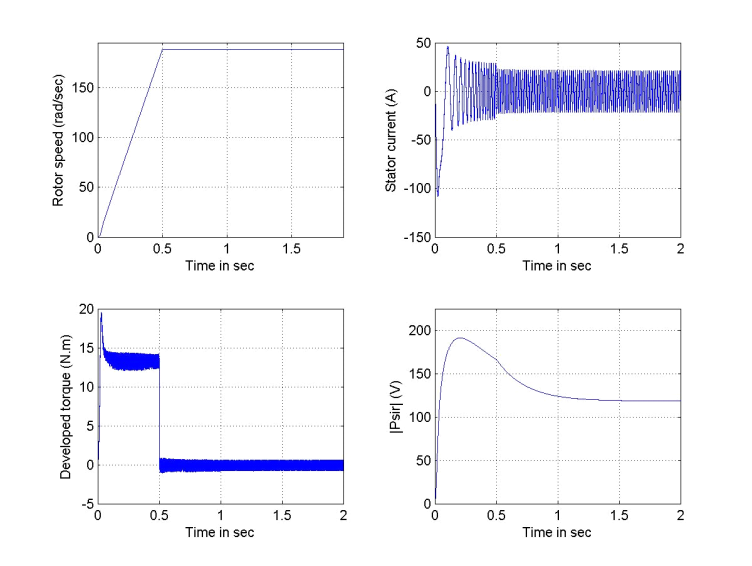 | Figure 6. Responses due to detuning effect (kr=0.5) with no-load |
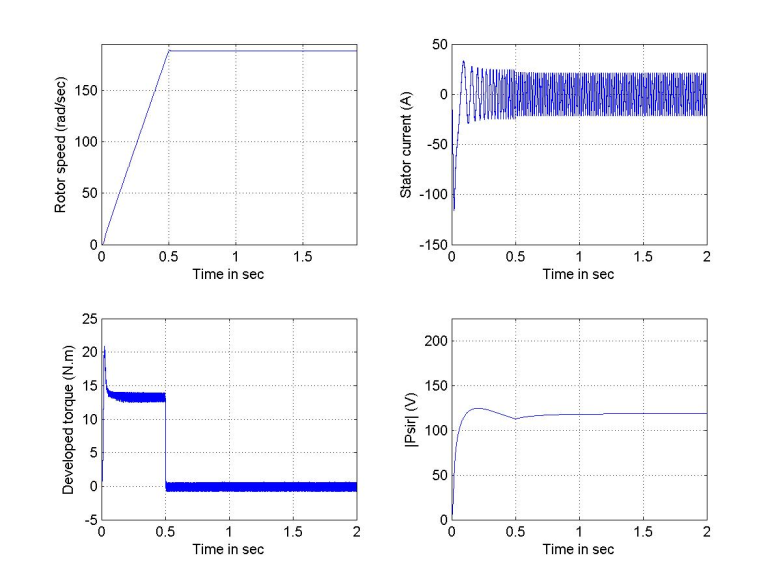 | Figure 7. Responses due to detuning effect (kr=1.5) with no-load |
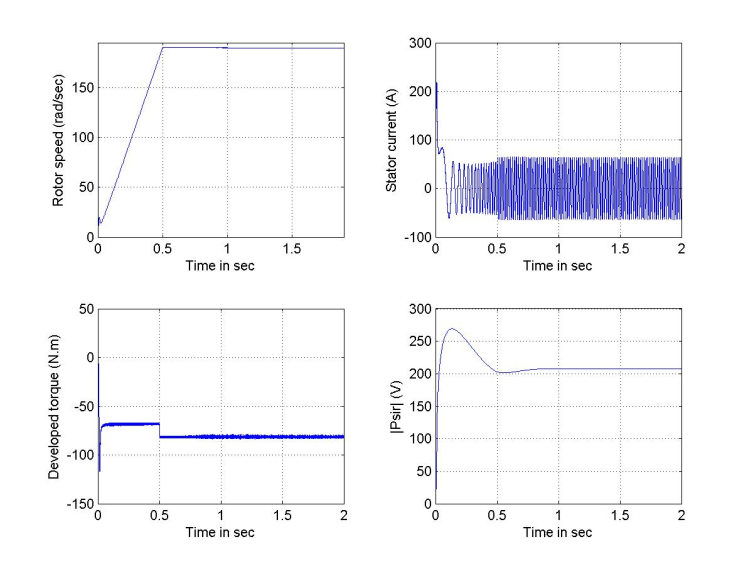 | Figure 8. Responses due to detuning effect (kr=0.5) with rated load torque |
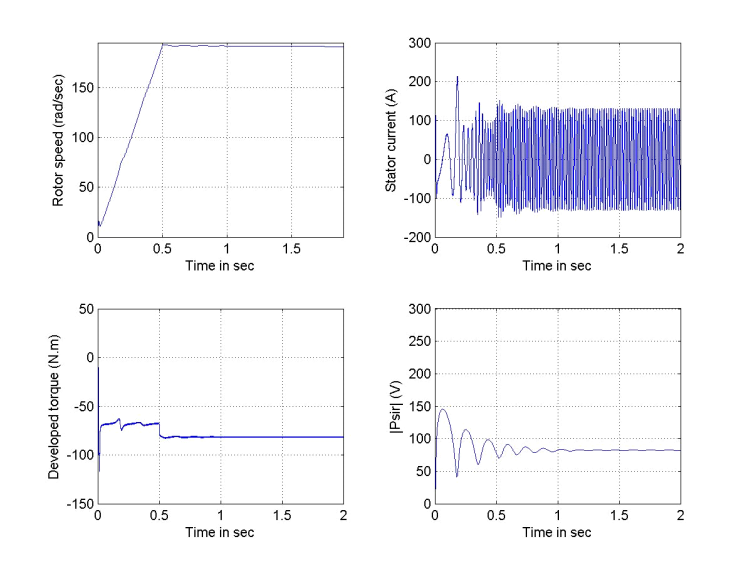 | Figure 9. Responses due to detuning effect (kr=1.5) with rated load torque |
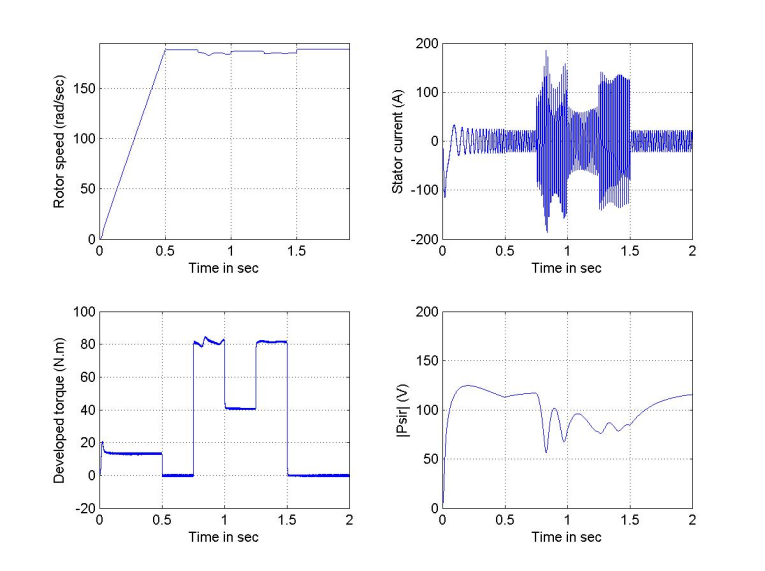 | Figure 10. Responses due to detuning effect (kr=1.5) with cyclic load changes |
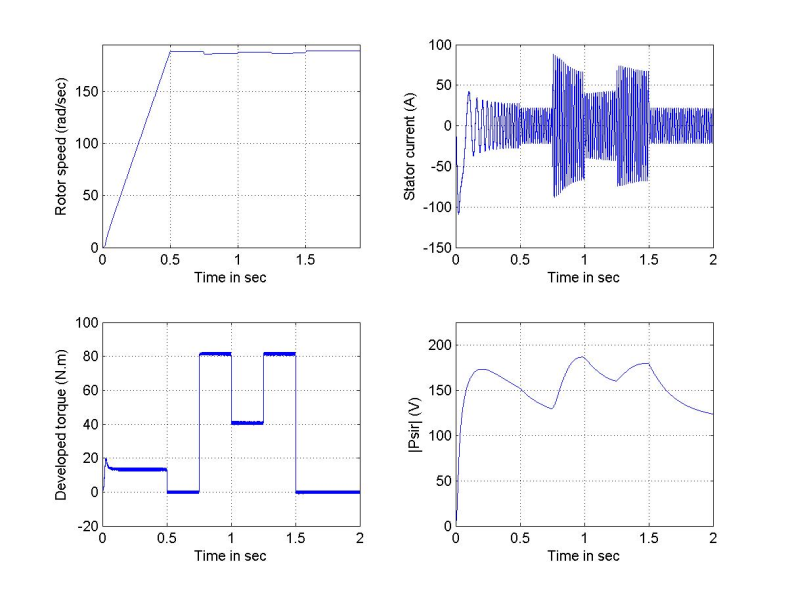 | Figure 11. Responses due to detuning effect (kr=0.625) with cyclic load changes |
5. Conclusions
- The implementation of IFOC technique has been performed and the following observations could be concluded:1. he technique can keep the rotor flux constant even during changes in load torque. This indicates that decoupling control of flux and torque has been obtained.2. It has been shown that decoupling is conditioned by the accuracy of slip calculation. The slip calculation depends on the rotor time constant,
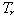 , which varies continuously according to the operational conditions.3. On the other hand, the conventional PI controller can not compensate such parameter variations in the plant. That is, the PI controller is not an intelligent controller nor is the slip calculation accurate. Therefore, changes in
, which varies continuously according to the operational conditions.3. On the other hand, the conventional PI controller can not compensate such parameter variations in the plant. That is, the PI controller is not an intelligent controller nor is the slip calculation accurate. Therefore, changes in 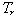 degrade the speed performance and other controllers can been suggested.
degrade the speed performance and other controllers can been suggested.ACKNOWLEDGEMENTS
- Rami A. Maher received the M.S. and Ph.D. degrees in technical cybernetics in 1982 and 1986 from VAAZ -Brno-Czechoslovakia. Since 2007 he has been with Isra-University-Jordan. His main research interests include automatic control theory, and controller design for electromechanical systems, RamiAmahir@yahoo.com.Walid Emar received the M.Sc. degree in industrial electronics and the Ph.D. degree in automatic control from West Bohemia University, Czech Republic. Currently, He is now teaching at Al-Isra Private University in Jordan as a full-time assistant professor. He is engaged in research of high power multilevel converters for industrial and traction applications, as well as dc/dc regulators,WalidEmar@yahoo.com.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML