Hanzel Lárez , Hugo Leiva , Darwin Mendoza
Departamento de Matemática, Universidad de Los Andes, Mérida, 5101, Venezuela
Correspondence to: Hugo Leiva , Departamento de Matemática, Universidad de Los Andes, Mérida, 5101, Venezuela.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper we prove the interior controllability of the following Timoshenko Type Equation 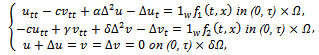 where Ω is a sufficiently regular bounded domined in
where Ω is a sufficiently regular bounded domined in 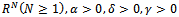 and
and 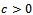 such that
such that 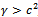 ,ω is an open nonempty subset of Ω, 1ω denotes the characteristicfunction of the set ω and the distributed control
,ω is an open nonempty subset of Ω, 1ω denotes the characteristicfunction of the set ω and the distributed control 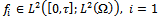 . Specifically, we prove the following statement: For all
. Specifically, we prove the following statement: For all 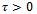 the system is approximatelycontrollable on
the system is approximatelycontrollable on 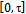 . Moreover, we exhibit a sequence of controls steering thesystem from an initial state to a
. Moreover, we exhibit a sequence of controls steering thesystem from an initial state to a 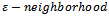 final state in a prefixed time
final state in a prefixed time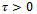 .
.
Keywords:
Interior Controllability, Timoshenko Type Equation, Strongly Continuous Semigroups
Cite this paper:
Hanzel Lárez , Hugo Leiva , Darwin Mendoza , "Interior Controllability of a Timoshenko Type Equation", International Journal of Control Science and Engineering, Vol. 1 No. 1, 2011, pp. 15-21. doi: 10.5923/j.control.20110101.03.
1. Introducción
The Timoshenko beam theory was developed by Ukrainian-born scientist Stephen Timoshenko in the beginning of the 20th century. The model takes into account shear deformation and rotational inertia effects, making it suitable for describing the behavior of short beams, sandwich composite beams or beams subject to high-frequency excitation when the wavelength approaches the thickness of the beam. The resulting equation is of 4th order, but unlike ordinary beam theory - i.e. Bernoulli-Euler theory, there is also a second order spatial derivative present. Physically, taking into account the added mechanisms of deformation effectively lowers the stiffness of the beam, while the result is a larger deflection under a static load and lower predicted eigenfrequencies for a given set of boundary conditions. The latter effect is more noticeable for higher frequencies as the wavelength becomes shorter, and thus the distance between opposing shear forces decreases. This paper has been motivated by the works in[2],[8],[9],[10],[12] and[13], where a new technique is used to prove the approximate controllability of some diffusion process.Following[2],[9] and[13], in this paper we study the interior approximate controllability of the following Timoshenko Type Equation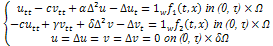 | (1) |
Where Ω is a sufficiently regular bounded domain in 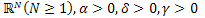 and
and 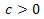 such that
such that 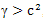 , ω is an open nonempty subset of
, ω is an open nonempty subset of 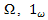 , denotes the characteristic function of the set ω and the distributed control
, denotes the characteristic function of the set ω and the distributed control 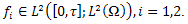 Specifically, we prove the following statement: For all
Specifically, we prove the following statement: For all 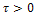 the system is approximately controllable on
the system is approximately controllable on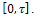 Moreover, we exhibit a sequence of controls steering the system from an initial state to a final state in a prefixed time
Moreover, we exhibit a sequence of controls steering the system from an initial state to a final state in a prefixed time 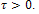 But, before proving this result, we study the approximate controllability of the following Timoshenkotype equation with the controls acting in the whole set Ω using some result from[8].
But, before proving this result, we study the approximate controllability of the following Timoshenkotype equation with the controls acting in the whole set Ω using some result from[8].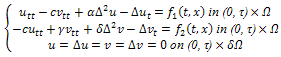 | (2) |
Where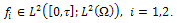 .Of course, the interior approximate controllability of this equation is more interesting problem from the applications point of view since the control is acting only in a subset or part of Ω. Our technique is simple and rests on the shoulders of the following fundamental results:Theorem 1.1.[10] The eigenfunctions of -Δ withDirichlet boundary condition on
.Of course, the interior approximate controllability of this equation is more interesting problem from the applications point of view since the control is acting only in a subset or part of Ω. Our technique is simple and rests on the shoulders of the following fundamental results:Theorem 1.1.[10] The eigenfunctions of -Δ withDirichlet boundary condition on 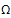 are real analytic functions.Theorem 1.2.[1]Suppose
are real analytic functions.Theorem 1.2.[1]Suppose 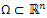 is an open, nonempty and connected set, and f is areal analytic function in Ω with
is an open, nonempty and connected set, and f is areal analytic function in Ω with 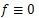 on a non-empty open subset ω of Ω. Then
on a non-empty open subset ω of Ω. Then 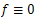 in Ω.
in Ω.
2. Abstract Formulation of the Problem
Let 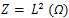 and consider the linear unbounded operator
and consider the linear unbounded operator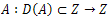 defined by
defined by 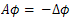 , where
, where 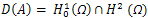 | (3) |
The operator A has the following very well known properties: the spectrum of A consists of only eigenvalues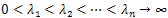 ,each one with multiplicity
,each one with multiplicity 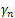 equal to the dimension of the corresponding eigenspace.a) There exists a complete orthonormal set
equal to the dimension of the corresponding eigenspace.a) There exists a complete orthonormal set 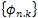 of eigenvectors of A.b) For all
of eigenvectors of A.b) For all 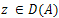 we have
we have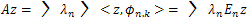 | (4) |
Where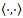 is the inner product in X and
is the inner product in X and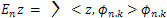 | (5) |
So, 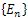 is a family of complete orthogonal projections in z and
is a family of complete orthogonal projections in z and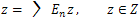 | (6) |
c) 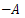 generates an analytic semigroup
generates an analytic semigroup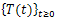 given by
given by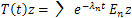 | (7) |
d) The fractional powered spaces 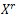 are given by:
are given by: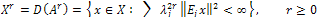 ,with the norm
,with the norm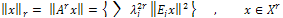 ,And
,And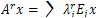 | (8) |
Also, for 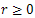 we define
we define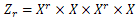 , which is a Hilbert Space with norm givenby
, which is a Hilbert Space with norm givenby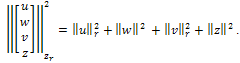 Hence, the equations (1) and (2) can be written as abstract systems of ordinary differential equations in the Hilbert space
Hence, the equations (1) and (2) can be written as abstract systems of ordinary differential equations in the Hilbert space | (9) |
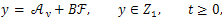 | (10) |
where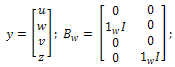 | (11) |
and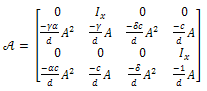 | (12) |
is a linear unbounded operator with domain 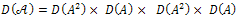 and
and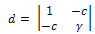 Now, using the following Lemma from[11] we can prove that the linear unbounded operator
Now, using the following Lemma from[11] we can prove that the linear unbounded operator 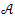 given by the linear equation (9) generates a strongly continuous semigroup which decays exponentially to zero.Lemma2.1.Let Z be a separable Hilbert space and
given by the linear equation (9) generates a strongly continuous semigroup which decays exponentially to zero.Lemma2.1.Let Z be a separable Hilbert space and 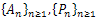 two families of bounded linear operators in Z with
two families of bounded linear operators in Z with 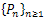 being a complete family of orthogonal projections such that
being a complete family of orthogonal projections such that | (13) |
Define the following family of linear operators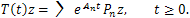 | (14) |
Thena) T(t) is a linear bounded operator if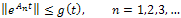 | (15) |
for some continuous real-valued function g(t).b) Under the condition (15) 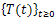 is a C0 -semigroup in the Hilbert space Z whose infinitesimal generator
is a C0 -semigroup in the Hilbert space Z whose infinitesimal generator 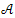 is given by
is given by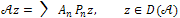 | (16) |
With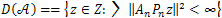 | (17) |
c) The spectrum 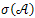 of
of 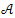 is given by
is given by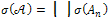 | (18) |
Theorem 2.2.The operator 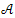 given by (12) is the infinitesimal generator of a strongly continuo semigroup
given by (12) is the infinitesimal generator of a strongly continuo semigroup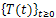 represented by
represented by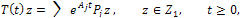 | (19) |
Where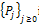 is a complete family orthogonal projections in the Hilbert space
is a complete family orthogonal projections in the Hilbert space 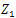 given by
given by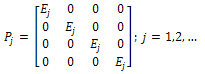 | (20) |
and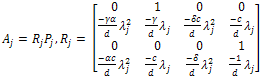 | (21) |
Where 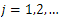 Therefore,
Therefore, 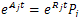 , the ingenvalues
, the ingenvalues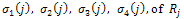 are simple and
are simple and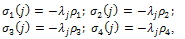 Where
Where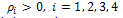 are the roots of the characteristic equation
are the roots of the characteristic equation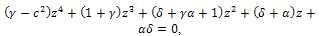 and this semigroup decays exponentially to zero; that is to say,
and this semigroup decays exponentially to zero; that is to say,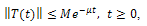 where
where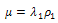 and
and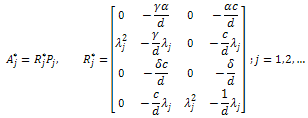 The following gap condition plays an important role in this paper
The following gap condition plays an important role in this paper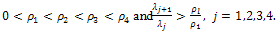 | (22) |
3. Controllability of the System (10)
In this section we shall prove the approximate controllability of the system (10). But, before we shall give the definition of approximate controllability for this system. To this end, for all 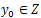 and
and 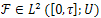 the initial value problem
the initial value problem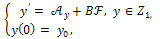 | (23) |
were 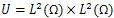 , admits only one mild solution given by
, admits only one mild solution given by 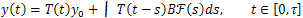 | (24) |
Definition 3.1.(Approximate Controllability) The system (10) is said to be approximately controllable on 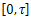 if for every
if for every 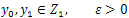 there exists
there exists 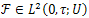 such that the solution
such that the solution 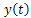 of (23) corresponding to
of (23) corresponding to 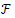 verifies:Definition 3.2. For the system (10) we define the following concepts:a) The controllability mapping
verifies:Definition 3.2. For the system (10) we define the following concepts:a) The controllability mapping 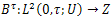 is defined by
is defined by 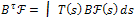 | (25) |
b) The grammian mapping 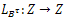 is given bythat is to say
is given bythat is to say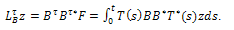 Theorem 3.3.The system (10) is approximately controllable on
Theorem 3.3.The system (10) is approximately controllable on 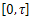 if, and only if, one of the following statements holds:
if, and only if, one of the following statements holds: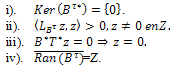 Proposition 3.4.The following equality holds:
Proposition 3.4.The following equality holds: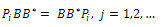 | (26) |
Prof.From (11) we know that  Then,
Then, 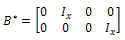 And
And 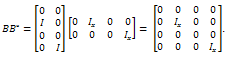 Since
Since 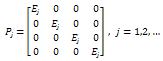 we get that
we get that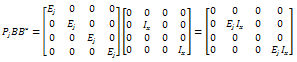 On the other hand,
On the other hand,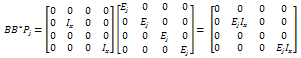 Therefore,
Therefore,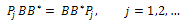 REMARK 3.1.If ω is a nonempty open sub set of Ω such that
REMARK 3.1.If ω is a nonempty open sub set of Ω such that 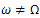 , then
, then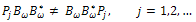 Now, we shall use the equality (26) in order to characterize the approximate control ability of the system (10) in terms of the following family of finite dimensional control problems,
Now, we shall use the equality (26) in order to characterize the approximate control ability of the system (10) in terms of the following family of finite dimensional control problems,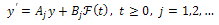 | (27) |
where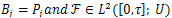 Proposition 3.5. The operator
Proposition 3.5. The operator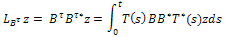 can be written as follows
can be written as follows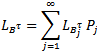 where,
where,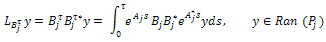 Proof. From condition (26) and the representation (19) of T(t) we obtain
Proof. From condition (26) and the representation (19) of T(t) we obtain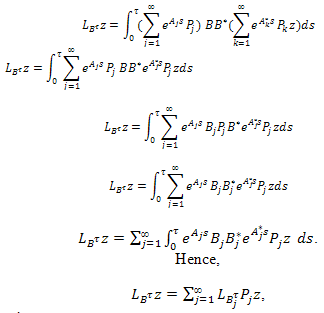 where,
where,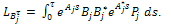 Theorem 3.6.a) The system (10) is approximately controllable on
Theorem 3.6.a) The system (10) is approximately controllable on 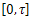 if, and only if, each of the following system
if, and only if, each of the following system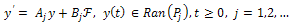 | (28) |
is approximately controllable.b)The system (10) is approximately controllable on 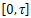 if, and only if
if, and only if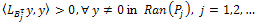 Proof.a) For the purpose of contradiction, let us assume that system (10) is approximately controllable on
Proof.a) For the purpose of contradiction, let us assume that system (10) is approximately controllable on 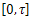 and there exists j such that the system
and there exists j such that the system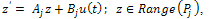 is not approximately controllable on
is not approximately controllable on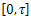 . Then, there exists
. Then, there exists 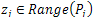 such that:
such that: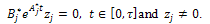 | (29) |
On the other hand, from part (iii) of Theorem 3.3 we have that: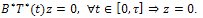 Now, letting
Now, letting 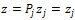 , we obtain:
, we obtain: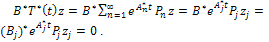 This implies that
This implies that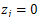 , which contradicts the assumption. Therefore, (28) is approximately controllable for all j.If for all j system (28) is approximately controllable, then by Theorem 3.3 part (ii),
, which contradicts the assumption. Therefore, (28) is approximately controllable for all j.If for all j system (28) is approximately controllable, then by Theorem 3.3 part (ii),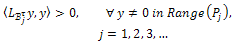 Clearly that, for all
Clearly that, for all 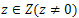 , there exists
, there exists 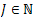 such that
such that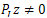 . Then, using Proposition 3.5, we get for all z in Z that
. Then, using Proposition 3.5, we get for all z in Z that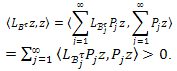 Hence, (10) is approximately controllable and (a) is proved.b) follows immediately from (a) and Theorem 3.3.Next, we shall use the following result: Consider the following finite dimensional controlsystem
Hence, (10) is approximately controllable and (a) is proved.b) follows immediately from (a) and Theorem 3.3.Next, we shall use the following result: Consider the following finite dimensional controlsystem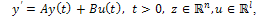 | (30) |
Where A and B are matrixes of dimensions 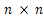 and
and 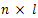 respectively.Theorem 3.7. (see[Lee and Marcus(1967)]). (Kalman) The system (30) is controllably on
respectively.Theorem 3.7. (see[Lee and Marcus(1967)]). (Kalman) The system (30) is controllably on 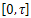 if, and only if,
if, and only if,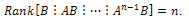 That is to say,
That is to say,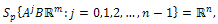 where
where 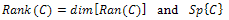 is the vector space generated by
is the vector space generated by 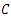 .Theorem 3.8. The system (10) is approximatelycontroll-able on
.Theorem 3.8. The system (10) is approximatelycontroll-able on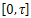 .Proof. It is enough to prove the controllability of the finite dimensional system (28) with
.Proof. It is enough to prove the controllability of the finite dimensional system (28) with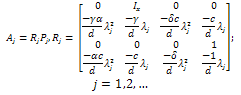 and
and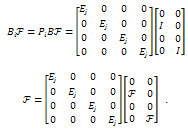 So,
So,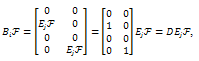 where
where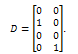 Therefore, the controllability of the system (28) is equivalent to the controllability of each finite dimensional systems,
Therefore, the controllability of the system (28) is equivalent to the controllability of each finite dimensional systems,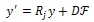 | (31) |
where,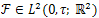 and the system (31) is controllable if, and only if,
and the system (31) is controllable if, and only if,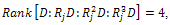 which can be verified trivially. Therefore, system (31) is controllable, and consequently, system (10) is also approximately controllable applying Theorem 3.6.
which can be verified trivially. Therefore, system (31) is controllable, and consequently, system (10) is also approximately controllable applying Theorem 3.6.
4. Proof of the Main Theorem
In this section we shall prove the main result of this paper on the approximate controllability of the linear system (9). To this end, we observe that the definition of controllability for system (9) is similar to the one given to system (10). And, for all 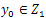 and
and 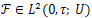 the initial value problem
the initial value problem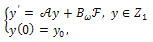 | (32) |
admits only one mild solution given by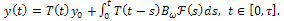 | (33) |
Consider the following bounded linear operator: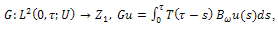 | (34) |
Whose adjoint operator 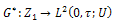 is given by
is given by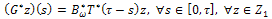 | (35) |
The following lemma is trivial:Lemma 4.1.The equation (9) is approximately controllable on 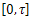 if, and only if,
if, and only if,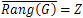 .The following result is well known from linear operator theory:Lemma 4.2.Let W and Z be Hilbert spaces and
.The following result is well known from linear operator theory:Lemma 4.2.Let W and Z be Hilbert spaces and 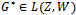 the adjoint operator of the linear operator
the adjoint operator of the linear operator 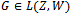 . Then,
. Then,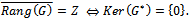 As a consequence of the foregoing Lemma one can prove the following result:Lemma 4.3.Let W and Z be Hilbert spaces and
As a consequence of the foregoing Lemma one can prove the following result:Lemma 4.3.Let W and Z be Hilbert spaces and 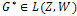 the adjoint operator of the linear operator
the adjoint operator of the linear operator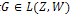 Then
Then 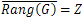 if, and only if, one of the following statements holds:
if, and only if, one of the following statements holds: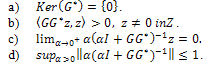 The following theorem follows directly from (35), lemma 4.1 and lemma 4.3.Theorem 4.4.(9) is approximately controllable on
The following theorem follows directly from (35), lemma 4.1 and lemma 4.3.Theorem 4.4.(9) is approximately controllable on 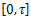 if, and only if,
if, and only if,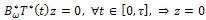 | (36) |
For the proof of the main theorem of this paper we shall use the following version ofLemma 3.14 from [3] and Lemma 4.4 from [2].Lemma 4.5.Let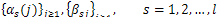 be sequences of real numbers such that
be sequences of real numbers such that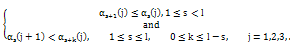 | (37) |
Then, for any 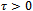 we have that
we have that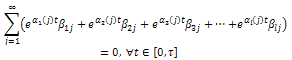 | (38) |
if, and only if,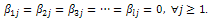 | (39) |
Proof. (Lemma 4.5) By analytic extension we obtain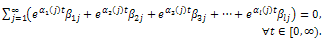 | (40) |
Now, dividing this expression by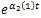 we get
we get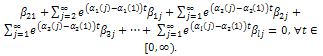 From (37) we have that
From (37) we have that 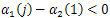 and
and 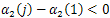 for
for 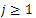 and
and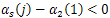 , for
, for , then passing to the limit when
, then passing to the limit when 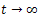 we obtain that
we obtain that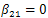 .Then, we have that
.Then, we have that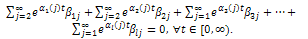 Now, dividing this expression by
Now, dividing this expression by 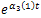 we get
we get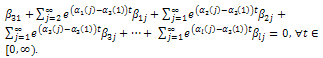 From (37) we have that
From (37) we have that 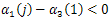 and
and 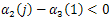 for
for 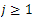 and
and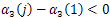 , for
, for 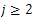 , then passing to the limit when
, then passing to the limit when 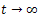 we obtain that
we obtain that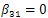 .Then, we have that
.Then, we have that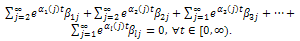 In general, if we continue with this process and divide this expression by
In general, if we continue with this process and divide this expression by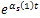 , we get that
, we get that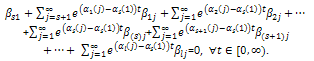 From (37) we have that
From (37) we have that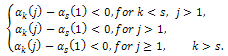 Then, passing to the limit when
Then, passing to the limit when 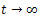 we obtain that
we obtain that 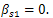 So, continuing with this procedure we get that
So, continuing with this procedure we get that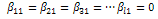 and
and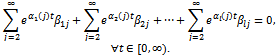 Repeating this procedure from here, we would obtain that
Repeating this procedure from here, we would obtain that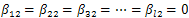 ,and continuing this way we get
,and continuing this way we get 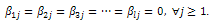 Now, we are ready to formulate and prove the main theorem of this work.Theorem 4.6.(Main Result) For all nonempty open subset ωof Ω and
Now, we are ready to formulate and prove the main theorem of this work.Theorem 4.6.(Main Result) For all nonempty open subset ωof Ω and 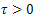 the system(9) is approximately controllable on
the system(9) is approximately controllable on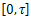 . Moreover, a sequence of controls steering thesystem (9) from initial state
. Moreover, a sequence of controls steering thesystem (9) from initial state 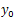 to an
to an 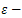 neighborhood of the final state
neighborhood of the final state 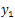 at time
at time 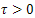 is given by
is given by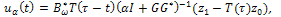 and the error of this approximation
and the error of this approximation 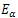 is given by
is given by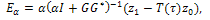 Proof. We shall apply Theorem 4.4 to prove the controllability of system (9). To this end, we observe that
Proof. We shall apply Theorem 4.4 to prove the controllability of system (9). To this end, we observe that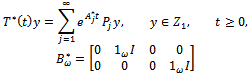 and, since the eigenvalues of the matrix
and, since the eigenvalues of the matrix 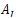 are simple, there exists a family of complete complementary projections
are simple, there exists a family of complete complementary projections 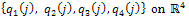 such that
such that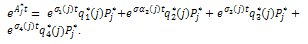 Therefore,
Therefore,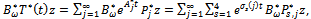 where
where 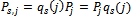 Now, suppose that
Now, suppose that 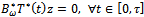 . Then,
. Then,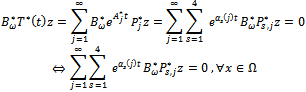 The assumption (22) implies that the sequence
The assumption (22) implies that the sequence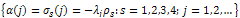 satisfies the conditions on Lemma 4.5. In fact, we have trivially that
satisfies the conditions on Lemma 4.5. In fact, we have trivially that 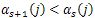 for
for 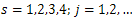 and from (22) we obtain:
and from (22) we obtain: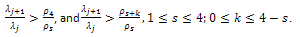 Therefore,
Therefore,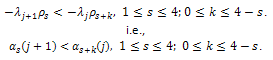 Then, from Lemma 4.5 we obtain for all
Then, from Lemma 4.5 we obtain for all 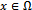 that
that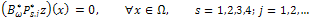 Since
Since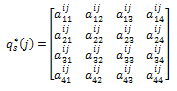 we obtain that,
we obtain that,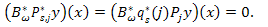 Then,
Then,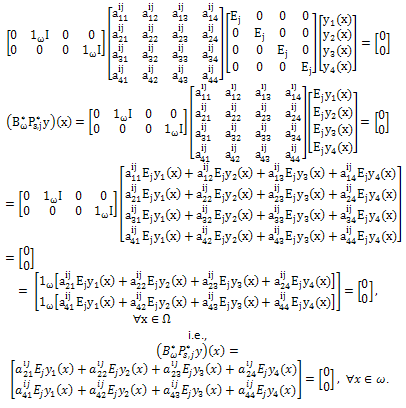 On the other hand, from Theorem 1.1 we know that
On the other hand, from Theorem 1.1 we know that 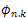 are analytic functions, which implies the analyticity of
are analytic functions, which implies the analyticity of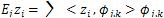 . Then, from Theorem 1.2 we get for
. Then, from Theorem 1.2 we get for 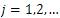 that
that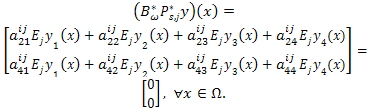 From Theorem 3.8, the system (10) is approximately controllable. So, from part iii) of Theorem 3.3 we conclude that
From Theorem 3.8, the system (10) is approximately controllable. So, from part iii) of Theorem 3.3 we conclude that 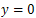 .Therefore,
.Therefore,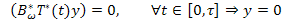 Then, from Theorem 4.4 we obtain that system (9) is approximately controllable.Now, given the initial and the final states
Then, from Theorem 4.4 we obtain that system (9) is approximately controllable.Now, given the initial and the final states 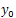 and
and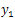 , we consider the sequence of controls
, we consider the sequence of controls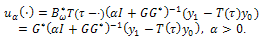 Then,
Then,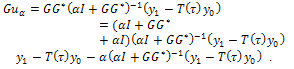 From part c) of Lemma 4.3 we know that
From part c) of Lemma 4.3 we know that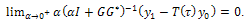 Therefore,
Therefore,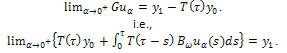 This completes the proof of the Theorem.Corollary 4.7.The approximate controllability of the system (9) is equivalent to the approximate controllability of the system (10).
This completes the proof of the Theorem.Corollary 4.7.The approximate controllability of the system (9) is equivalent to the approximate controllability of the system (10).
5. Final Remark
The result presented in this paper can be formulated in a more general setting. Indeed, we can consider the following Timoshenko Type Equation in a general Hilbert space Z and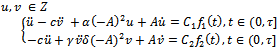 | (41) |
where, 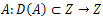 is an unbounded linear operator in Z with the spectral decomposition given by
is an unbounded linear operator in Z with the spectral decomposition given by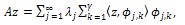 with eigenvalues
with eigenvalues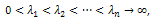 each one with multiplicity
each one with multiplicity 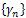 equal to the dimension of the corresponding eigenspace.a) There exists a complete orthonormal set
equal to the dimension of the corresponding eigenspace.a) There exists a complete orthonormal set 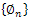 of eigenvectors of A.b) For all
of eigenvectors of A.b) For all 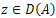 we havec)
we havec) 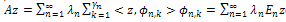 | (42) |
The controls 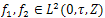 and
and 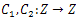 are linear and bounded.When
are linear and bounded.When 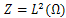 , the operators
, the operators 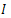 and
and 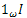 are particular cases of
are particular cases of 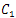 and
and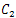 .
.
References
| [1] | S. Axler, P. Bourdon and W. Ramey, Harmonic Fucntion Theory. Graduate Texts in Math., 137. Springer Verlag, New York (1992). |
| [2] | Salah Badraoui, Approximate Controllability of a Reaction-Diffusion System with a Cross Diffusion Matrix and Fractional Derivatives on Bounded Domains, Journal of Boundary Value Problems, Vol. 2010, Art.ID 281238, 14pgs.(2010). |
| [3] | R.F. Curtain, A.J. Pritchard, Infinite Dimensional Linear Systems. Lecture Notes in Control and Information Sciences, 8. Springer Verlag, Berlin (1978). |
| [4] | R.F. Curtain, H.J. Zwart, An Introduction to Infinite Dimensional Linear Systems Theory. Text in Applied Mathematics, 21. Springer Verlag, New York (1995). |
| [5] | Luiz A. F. de Oliveira, On Reaction-Diffusion Systems” E. Journal of Differential Equations, Vol. 1998(1998), N0. 24, pp. 1-10. |
| [6] | Jong Uhn Kim, On the Energy Decay of a Linear Thermoelastic Bar and Plate. SIAM J. Math Anal.Vol.23, No. 4, pp 889, (1992). |
| [7] | J. Lagnese, Boundary Stabilization of Thin Plate. SIAM Studies in Appl. Math.10, Philadelphia. Controllability of Timoshenko Type Equation. 17,(1989). |
| [8] | H. Lárez, H. Leiva and J. Uzcátegui, Controllability of Block Diagonal Systems and Applications, Int. J. Systems, Control and Communications, Vol. 3, No. 1, (2011). |
| [9] | H. Lárez and H. Leiva, Interior controllability of a 2£2 reaction-diffusion system with cross-diffusion matrix, Boundary Value Problems, Vol. 2009, Article ID560407, 9 pages, doi:10.1155/2009/560407. |
| [10] | H. Leivaand Y. Quintana, Interior controllability of a broad class of reaction diffusion equation, Mathematical Problems in Engineering, Vol. 2009, Article ID708516, 8 pages, doi:10.1155/2009/708516. |
| [11] | H. Leiva, A Lemma on C0-Semigroups and Applications PDEs Systems Quaestions Mathematicae, Vol. 26, pp. 247-265 (2003). |
| [12] | H. Leiva, A necessary and sufficient algebraic condition for the controllability of thermoelastic plate equation, IMA Journal of Control and Information, pp.1-18, (2003). |
| [13] | H. Leivaand N. Merentes, Interior controllability of the thermoelastic plate equation, African Diaspora Journal of Mathematics, Vol. 12, N. 1, pp. 1-14 (2011). |
| [14] | Y. Shibata, On the Exponential Decay of the Energy of a Linear Thermoelastic Plate. Comp. Appl. Math. Vol. 13, No. 2, pp. 81-102,(1994). |

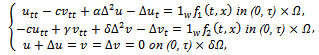 where Ω is a sufficiently regular bounded domined in
where Ω is a sufficiently regular bounded domined in 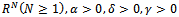 and
and 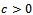 such that
such that 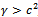 ,ω is an open nonempty subset of Ω, 1ω denotes the characteristicfunction of the set ω and the distributed control
,ω is an open nonempty subset of Ω, 1ω denotes the characteristicfunction of the set ω and the distributed control 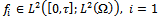 . Specifically, we prove the following statement: For all
. Specifically, we prove the following statement: For all 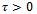 the system is approximatelycontrollable on
the system is approximatelycontrollable on 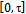 . Moreover, we exhibit a sequence of controls steering thesystem from an initial state to a
. Moreover, we exhibit a sequence of controls steering thesystem from an initial state to a 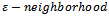 final state in a prefixed time
final state in a prefixed time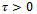 .
.
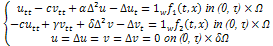
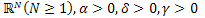 and
and 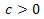 such that
such that 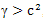 , ω is an open nonempty subset of
, ω is an open nonempty subset of 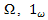 , denotes the characteristic function of the set ω and the distributed control
, denotes the characteristic function of the set ω and the distributed control 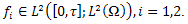 Specifically, we prove the following statement: For all
Specifically, we prove the following statement: For all 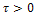 the system is approximately controllable on
the system is approximately controllable on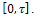 Moreover, we exhibit a sequence of controls steering the system from an initial state to a final state in a prefixed time
Moreover, we exhibit a sequence of controls steering the system from an initial state to a final state in a prefixed time 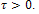 But, before proving this result, we study the approximate controllability of the following Timoshenkotype equation with the controls acting in the whole set Ω using some result from[8].
But, before proving this result, we study the approximate controllability of the following Timoshenkotype equation with the controls acting in the whole set Ω using some result from[8].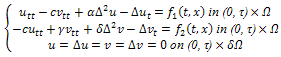
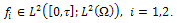 .Of course, the interior approximate controllability of this equation is more interesting problem from the applications point of view since the control is acting only in a subset or part of Ω. Our technique is simple and rests on the shoulders of the following fundamental results:Theorem 1.1.[10] The eigenfunctions of -Δ withDirichlet boundary condition on
.Of course, the interior approximate controllability of this equation is more interesting problem from the applications point of view since the control is acting only in a subset or part of Ω. Our technique is simple and rests on the shoulders of the following fundamental results:Theorem 1.1.[10] The eigenfunctions of -Δ withDirichlet boundary condition on 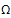 are real analytic functions.Theorem 1.2.[1]Suppose
are real analytic functions.Theorem 1.2.[1]Suppose 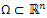 is an open, nonempty and connected set, and f is areal analytic function in Ω with
is an open, nonempty and connected set, and f is areal analytic function in Ω with 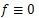 on a non-empty open subset ω of Ω. Then
on a non-empty open subset ω of Ω. Then 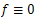 in Ω.
in Ω.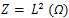 and consider the linear unbounded operator
and consider the linear unbounded operator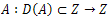 defined by
defined by 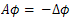 , where
, where 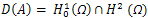
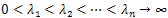 ,each one with multiplicity
,each one with multiplicity 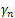 equal to the dimension of the corresponding eigenspace.a) There exists a complete orthonormal set
equal to the dimension of the corresponding eigenspace.a) There exists a complete orthonormal set 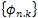 of eigenvectors of A.b) For all
of eigenvectors of A.b) For all 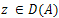 we have
we have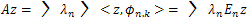
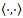 is the inner product in X and
is the inner product in X and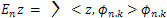
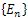 is a family of complete orthogonal projections in z and
is a family of complete orthogonal projections in z and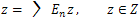
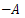 generates an analytic semigroup
generates an analytic semigroup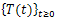 given by
given by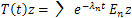
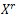 are given by:
are given by: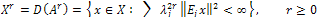 ,with the norm
,with the norm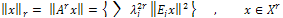 ,And
,And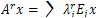
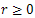 we define
we define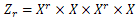 , which is a Hilbert Space with norm givenby
, which is a Hilbert Space with norm givenby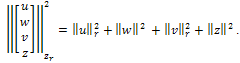 Hence, the equations (1) and (2) can be written as abstract systems of ordinary differential equations in the Hilbert space
Hence, the equations (1) and (2) can be written as abstract systems of ordinary differential equations in the Hilbert space
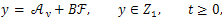
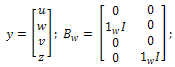
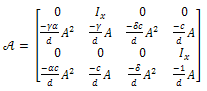
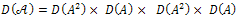 and
and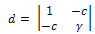 Now, using the following Lemma from[11] we can prove that the linear unbounded operator
Now, using the following Lemma from[11] we can prove that the linear unbounded operator 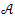 given by the linear equation (9) generates a strongly continuous semigroup which decays exponentially to zero.Lemma2.1.Let Z be a separable Hilbert space and
given by the linear equation (9) generates a strongly continuous semigroup which decays exponentially to zero.Lemma2.1.Let Z be a separable Hilbert space and 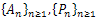 two families of bounded linear operators in Z with
two families of bounded linear operators in Z with 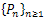 being a complete family of orthogonal projections such that
being a complete family of orthogonal projections such that
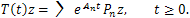
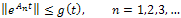
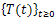 is a C0 -semigroup in the Hilbert space Z whose infinitesimal generator
is a C0 -semigroup in the Hilbert space Z whose infinitesimal generator 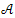 is given by
is given by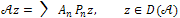
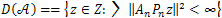
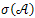 of
of 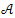 is given by
is given by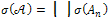
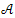 given by (12) is the infinitesimal generator of a strongly continuo semigroup
given by (12) is the infinitesimal generator of a strongly continuo semigroup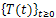 represented by
represented by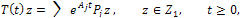
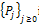 is a complete family orthogonal projections in the Hilbert space
is a complete family orthogonal projections in the Hilbert space 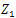 given by
given by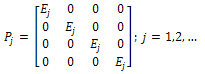
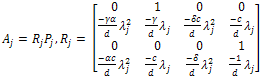
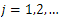 Therefore,
Therefore, 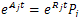 , the ingenvalues
, the ingenvalues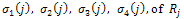 are simple and
are simple and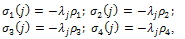 Where
Where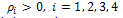 are the roots of the characteristic equation
are the roots of the characteristic equation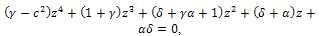 and this semigroup decays exponentially to zero; that is to say,
and this semigroup decays exponentially to zero; that is to say,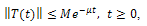 where
where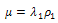 and
and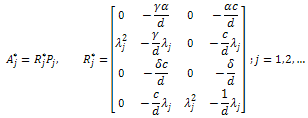 The following gap condition plays an important role in this paper
The following gap condition plays an important role in this paper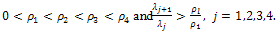
 and
and  the initial value problem
the initial value problem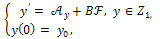
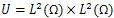 , admits only one mild solution given by
, admits only one mild solution given by 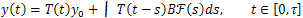
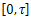 if for every
if for every 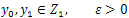 there exists
there exists 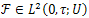 such that the solution
such that the solution 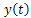 of (23) corresponding to
of (23) corresponding to 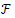 verifies:Definition 3.2. For the system (10) we define the following concepts:a) The controllability mapping
verifies:Definition 3.2. For the system (10) we define the following concepts:a) The controllability mapping 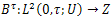 is defined by
is defined by 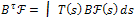
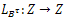 is given bythat is to say
is given bythat is to say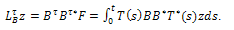 Theorem 3.3.The system (10) is approximately controllable on
Theorem 3.3.The system (10) is approximately controllable on 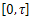 if, and only if, one of the following statements holds:
if, and only if, one of the following statements holds: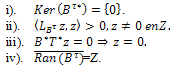 Proposition 3.4.The following equality holds:
Proposition 3.4.The following equality holds: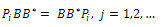
 Then,
Then, 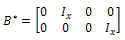 And
And 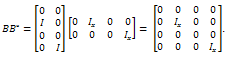 Since
Since 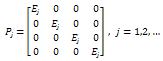 we get that
we get that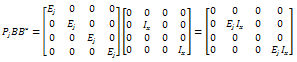 On the other hand,
On the other hand,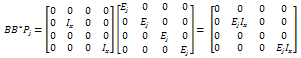 Therefore,
Therefore,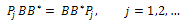 REMARK 3.1.If ω is a nonempty open sub set of Ω such that
REMARK 3.1.If ω is a nonempty open sub set of Ω such that 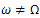 , then
, then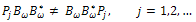 Now, we shall use the equality (26) in order to characterize the approximate control ability of the system (10) in terms of the following family of finite dimensional control problems,
Now, we shall use the equality (26) in order to characterize the approximate control ability of the system (10) in terms of the following family of finite dimensional control problems,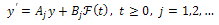
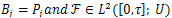 Proposition 3.5. The operator
Proposition 3.5. The operator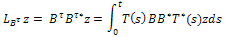 can be written as follows
can be written as follows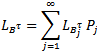 where,
where,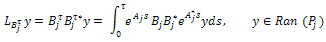 Proof. From condition (26) and the representation (19) of T(t) we obtain
Proof. From condition (26) and the representation (19) of T(t) we obtain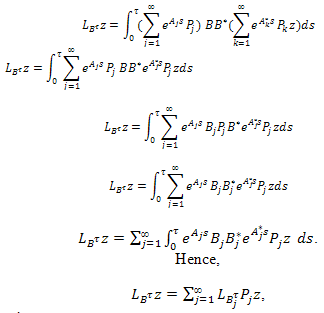 where,
where,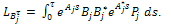 Theorem 3.6.a) The system (10) is approximately controllable on
Theorem 3.6.a) The system (10) is approximately controllable on 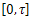 if, and only if, each of the following system
if, and only if, each of the following system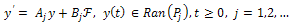
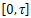 if, and only if
if, and only if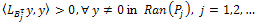 Proof.a) For the purpose of contradiction, let us assume that system (10) is approximately controllable on
Proof.a) For the purpose of contradiction, let us assume that system (10) is approximately controllable on 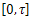 and there exists j such that the system
and there exists j such that the system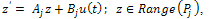 is not approximately controllable on
is not approximately controllable on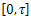 . Then, there exists
. Then, there exists 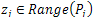 such that:
such that: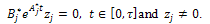
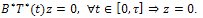 Now, letting
Now, letting 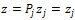 , we obtain:
, we obtain: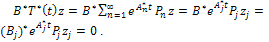 This implies that
This implies that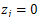 , which contradicts the assumption. Therefore, (28) is approximately controllable for all j.If for all j system (28) is approximately controllable, then by Theorem 3.3 part (ii),
, which contradicts the assumption. Therefore, (28) is approximately controllable for all j.If for all j system (28) is approximately controllable, then by Theorem 3.3 part (ii),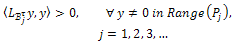 Clearly that, for all
Clearly that, for all 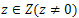 , there exists
, there exists 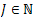 such that
such that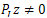 . Then, using Proposition 3.5, we get for all z in Z that
. Then, using Proposition 3.5, we get for all z in Z that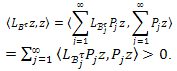 Hence, (10) is approximately controllable and (a) is proved.b) follows immediately from (a) and Theorem 3.3.Next, we shall use the following result: Consider the following finite dimensional controlsystem
Hence, (10) is approximately controllable and (a) is proved.b) follows immediately from (a) and Theorem 3.3.Next, we shall use the following result: Consider the following finite dimensional controlsystem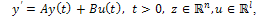
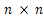 and
and 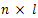 respectively.Theorem 3.7. (see[Lee and Marcus(1967)]). (Kalman) The system (30) is controllably on
respectively.Theorem 3.7. (see[Lee and Marcus(1967)]). (Kalman) The system (30) is controllably on 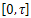 if, and only if,
if, and only if,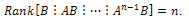 That is to say,
That is to say,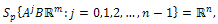 where
where 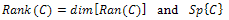 is the vector space generated by
is the vector space generated by 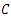 .Theorem 3.8. The system (10) is approximatelycontroll-able on
.Theorem 3.8. The system (10) is approximatelycontroll-able on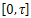 .Proof. It is enough to prove the controllability of the finite dimensional system (28) with
.Proof. It is enough to prove the controllability of the finite dimensional system (28) with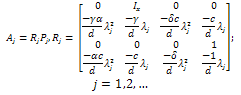 and
and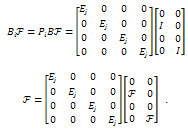 So,
So,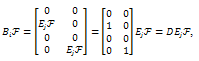 where
where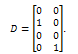 Therefore, the controllability of the system (28) is equivalent to the controllability of each finite dimensional systems,
Therefore, the controllability of the system (28) is equivalent to the controllability of each finite dimensional systems,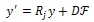
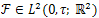 and the system (31) is controllable if, and only if,
and the system (31) is controllable if, and only if,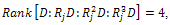 which can be verified trivially. Therefore, system (31) is controllable, and consequently, system (10) is also approximately controllable applying Theorem 3.6.
which can be verified trivially. Therefore, system (31) is controllable, and consequently, system (10) is also approximately controllable applying Theorem 3.6.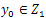 and
and 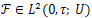 the initial value problem
the initial value problem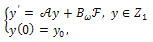
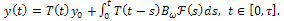
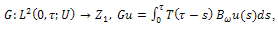
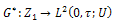 is given by
is given by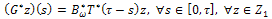
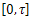 if, and only if,
if, and only if,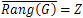 .The following result is well known from linear operator theory:Lemma 4.2.Let W and Z be Hilbert spaces and
.The following result is well known from linear operator theory:Lemma 4.2.Let W and Z be Hilbert spaces and 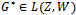 the adjoint operator of the linear operator
the adjoint operator of the linear operator 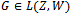 . Then,
. Then,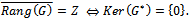 As a consequence of the foregoing Lemma one can prove the following result:Lemma 4.3.Let W and Z be Hilbert spaces and
As a consequence of the foregoing Lemma one can prove the following result:Lemma 4.3.Let W and Z be Hilbert spaces and 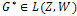 the adjoint operator of the linear operator
the adjoint operator of the linear operator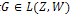 Then
Then 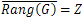 if, and only if, one of the following statements holds:
if, and only if, one of the following statements holds: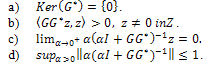 The following theorem follows directly from (35), lemma 4.1 and lemma 4.3.Theorem 4.4.(9) is approximately controllable on
The following theorem follows directly from (35), lemma 4.1 and lemma 4.3.Theorem 4.4.(9) is approximately controllable on 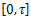 if, and only if,
if, and only if,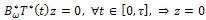
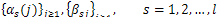 be sequences of real numbers such that
be sequences of real numbers such that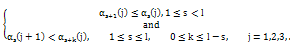
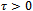 we have that
we have that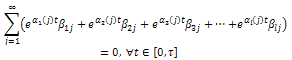
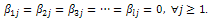
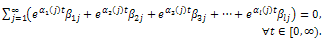
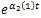 we get
we get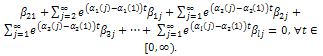 From (37) we have that
From (37) we have that 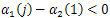 and
and 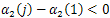 for
for 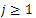 and
and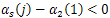 , for
, for , then passing to the limit when
, then passing to the limit when 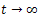 we obtain that
we obtain that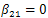 .Then, we have that
.Then, we have that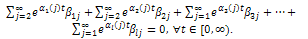 Now, dividing this expression by
Now, dividing this expression by 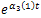 we get
we get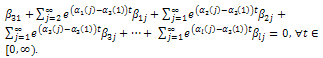 From (37) we have that
From (37) we have that 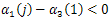 and
and 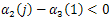 for
for 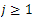 and
and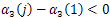 , for
, for 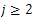 , then passing to the limit when
, then passing to the limit when 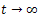 we obtain that
we obtain that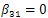 .Then, we have that
.Then, we have that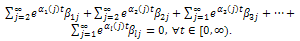 In general, if we continue with this process and divide this expression by
In general, if we continue with this process and divide this expression by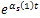 , we get that
, we get that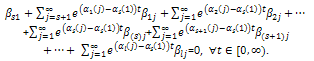 From (37) we have that
From (37) we have that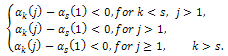 Then, passing to the limit when
Then, passing to the limit when 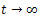 we obtain that
we obtain that 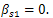 So, continuing with this procedure we get that
So, continuing with this procedure we get that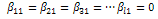 and
and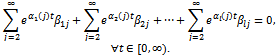 Repeating this procedure from here, we would obtain that
Repeating this procedure from here, we would obtain that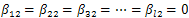 ,and continuing this way we get
,and continuing this way we get 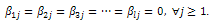 Now, we are ready to formulate and prove the main theorem of this work.Theorem 4.6.(Main Result) For all nonempty open subset ωof Ω and
Now, we are ready to formulate and prove the main theorem of this work.Theorem 4.6.(Main Result) For all nonempty open subset ωof Ω and 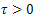 the system(9) is approximately controllable on
the system(9) is approximately controllable on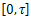 . Moreover, a sequence of controls steering thesystem (9) from initial state
. Moreover, a sequence of controls steering thesystem (9) from initial state 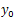 to an
to an 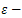 neighborhood of the final state
neighborhood of the final state 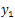 at time
at time 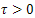 is given by
is given by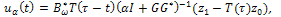 and the error of this approximation
and the error of this approximation 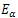 is given by
is given by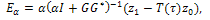 Proof. We shall apply Theorem 4.4 to prove the controllability of system (9). To this end, we observe that
Proof. We shall apply Theorem 4.4 to prove the controllability of system (9). To this end, we observe that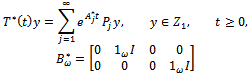 and, since the eigenvalues of the matrix
and, since the eigenvalues of the matrix 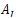 are simple, there exists a family of complete complementary projections
are simple, there exists a family of complete complementary projections 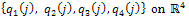 such that
such that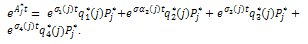 Therefore,
Therefore,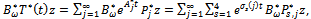 where
where 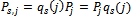 Now, suppose that
Now, suppose that 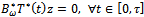 . Then,
. Then,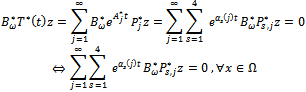 The assumption (22) implies that the sequence
The assumption (22) implies that the sequence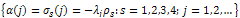 satisfies the conditions on Lemma 4.5. In fact, we have trivially that
satisfies the conditions on Lemma 4.5. In fact, we have trivially that 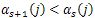 for
for 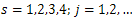 and from (22) we obtain:
and from (22) we obtain: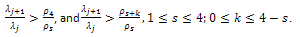 Therefore,
Therefore,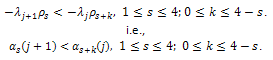 Then, from Lemma 4.5 we obtain for all
Then, from Lemma 4.5 we obtain for all 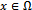 that
that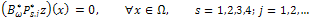 Since
Since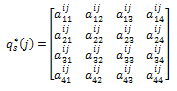 we obtain that,
we obtain that,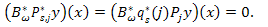 Then,
Then,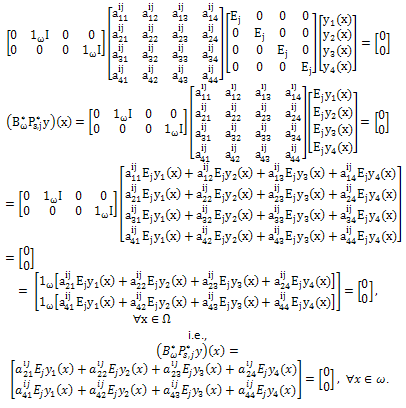 On the other hand, from Theorem 1.1 we know that
On the other hand, from Theorem 1.1 we know that  are analytic functions, which implies the analyticity of
are analytic functions, which implies the analyticity of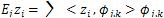 . Then, from Theorem 1.2 we get for
. Then, from Theorem 1.2 we get for 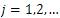 that
that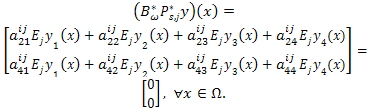 From Theorem 3.8, the system (10) is approximately controllable. So, from part iii) of Theorem 3.3 we conclude that
From Theorem 3.8, the system (10) is approximately controllable. So, from part iii) of Theorem 3.3 we conclude that 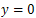 .Therefore,
.Therefore,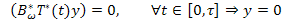 Then, from Theorem 4.4 we obtain that system (9) is approximately controllable.Now, given the initial and the final states
Then, from Theorem 4.4 we obtain that system (9) is approximately controllable.Now, given the initial and the final states 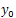 and
and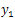 , we consider the sequence of controls
, we consider the sequence of controls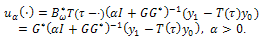 Then,
Then,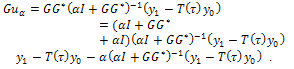 From part c) of Lemma 4.3 we know that
From part c) of Lemma 4.3 we know that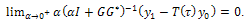 Therefore,
Therefore,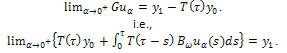 This completes the proof of the Theorem.Corollary 4.7.The approximate controllability of the system (9) is equivalent to the approximate controllability of the system (10).
This completes the proof of the Theorem.Corollary 4.7.The approximate controllability of the system (9) is equivalent to the approximate controllability of the system (10).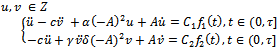
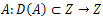 is an unbounded linear operator in Z with the spectral decomposition given by
is an unbounded linear operator in Z with the spectral decomposition given by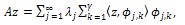 with eigenvalues
with eigenvalues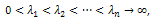 each one with multiplicity
each one with multiplicity 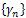 equal to the dimension of the corresponding eigenspace.a) There exists a complete orthonormal set
equal to the dimension of the corresponding eigenspace.a) There exists a complete orthonormal set 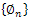 of eigenvectors of A.b) For all
of eigenvectors of A.b) For all 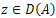 we havec)
we havec) 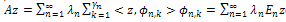
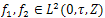 and
and 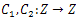 are linear and bounded.When
are linear and bounded.When 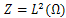 , the operators
, the operators 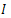 and
and 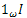 are particular cases of
are particular cases of 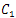 and
and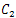 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML