M. M. Share Pasandand , H. D. Taghirad
Department of Systems and Control, Faculty of Electrical and Computer Engineering, Tehran, P.O. Box 16315-1355, Iran
Correspondence to: M. M. Share Pasandand , Department of Systems and Control, Faculty of Electrical and Computer Engineering, Tehran, P.O. Box 16315-1355, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper the problem of model based internal control of singular systems is investigated. The limitations of directly extending the control schemes for normal systems to singular ones are thoroughly developed, and a robust approach is proposed in order to establish a control scheme for singular systems. The proposed method presents a general framework for robust control design of singular systems in presence of modeling uncertainties. Two simulation examples are given to how the proposed method can be implemented, and to show the effectiveness of such controllers in closed loop performance.
Keywords:
Singular Systems, Impulsive Behaviour, Internal Model Control, Model Based Control, robust Control, Tracking Problem
Cite this paper:
M. M. Share Pasandand , H. D. Taghirad , "Robust Internal Model Control for Impulse Elimination of Singular Systems", International Journal of Control Science and Engineering, Vol. 1 No. 1, 2011, pp. 1-7. doi: 10.5923/j.control.20110101.01.
1. Introduction
Singular systems represent a more general framework for linear systems[1]. A singular model is an appropriate model for describing large scale interconnected systems, constrained robots and other differential algebraic systems with linear algebraic constraints[2].Also singular models can be utilized to model a system when the dependent variable is displacement and not the time[3]. Since the first time this representation is introduced[4], several efforts have been made to control singular systems[5-9]. As the singular systems were firstly introduced in the state space form representation[4], they were usually studied in time domain. In[5] the problem of finite mode pole placement is studied, while simultaneous impulse elimination and robust stabilization problem is considered in[6], robust Eigen-structure assignment of finite modes is studied in[7]. In[8] strict impulse elimination is studied using time derivative feedback of the states and[9] investigated the output feedback control using a compensator. In fact most of the existing methods are extensions of the control schemes for standard representation of such systems[5-10]. In the singular system control context the control objectives are more complicated due to the stringent requirements such as algebraic loop phenomenon, impulsive behaviour[11], and regularity of the closed loop[8,9]. Unlike the time domain methods, there are very few works on the frequency domain control of singular systems. In the frequency domain, the tracking problem, robust control problem and impulse elimination can be treated more convenient. Specifically the so called Internal Model Control (IMC) method provides a very interesting framework for analysing the algebraic loop, regularity of the closed loop and impulse elimination problems of singular systems. Furthermore, most of existing methods in robust control of singular systems are limited to study a special case of uncertainty. They assumed matrix E to be exactly known [6,7,10]. This assumption is more restrictive than it appears, because it limits the system to be impulsive while some uncertainties may exist, which lead to a strictly proper system for a singular model. The internal model framework for controlling singular systems provides a more logical uncertainty model and release the restrictive assumptions made in the existing state space methods for robust control of singular systems. Also it provides offset free tracking capability of the closed loop as well as being able to well treat delayed systems. The main challenge which arises in the internal model control of singular systems is that the internal model cannot be modelled easily, because it is generally improper. Even in computer aided control systems it is not easy to simulate a singular system, since the discrete model needs future input data to determine the system state vector at the present time[1]. This problem results in an inevitable mismatch between the plant and the parallel model used in IMC. Therefore, the robust control scheme should be extended to tackle this situation, which is fully examined in this paper.Note that, general disk shaped representation of modelling uncertainty leads to an unbounded uncertainty profile, and is not suitable for robust design of singular systems. This paper provides a solution to this problem by introducing a singular internal model filter in series with the conventional internal model filter. This filter not only eases the design procedure, but also bounds the uncertainty profile and offers more degrees of freedom in the design by introducing an additional filter time constant. Also it makes the closed loop system to become strictly proper and eliminates impulsive modes by smoothing the control action as much as needed. Another role of the introduced filter is to make it possible to design robust controller in the conventional context. The paper is organized as follows. In the next section backgrounds are discussed and the challenges arising in control of singular systems are presented, and some major limitations of the direct extension of IMC is explained. In the third section the proposed method is studied and the filter design procedure is illustrated. In the fourth section the examples and simulations are given to examine the algorithm both in terms of robustness properties and closed loop performance. Finally, the concluding remarks are given in last section.
2. Control Objectives in Singular Control Systems
2.1. Definitions and Singular Systems Characteristics
As Descriptor models are a straight extension of standard state space models[1], control problem for these systems has a wider range of objectives. A control system for a standard plant is designed such that the closed loop is stable and has a predefined performance and acceptable robustness properties. A singular control system, on the other hand, should be designed such that it is impulse free, regular and doesn’t include any algebraic loops in addition to the aforementioned properties. These control objectives combined with the standard objectives make the control of singular systems more challenging. Robust control of singular systems is the most stringent requirement, since it requires robustness not only in the stability and performance, but also it necessitates regularity and properness. State space robust control schemes require robust observers in order to work properly and do not guarantee strict properness of the closed loop system, and they usually result in more complicated derivation algorithms. The main advantage of using internal model control scheme in here is to provide an effective tool in frequency domain without introducing complicated methods in evaluation of closed loop performance and stability. Therefore, IMC can be regarded as a proper alternative for existing state space methods. Moreover, IMC provides a simple framework for algebraic loop and properness analysis of singular control systems, which is relatively much simpler than that in state space methods or other frequency domain schemes. Consider the following state space description: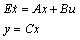 | (1) |
Definition1:System (1) is impulse free if and only if: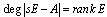 | (2) |
The nullity index of E is called singularity index of a singular system (1) in this paper. Remark1: Note that the following general inequality always holds: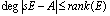 | (3) |
Corollary1: A singular system described by the following state space equations is called impulse free, if and only if, it doesn’t exhibit impulses in its impulse response.Definition2: A singular system is called minimal if it is observable and controllable. Definition3: A transfer function is strictly proper, bi-proper and improper if the following limit is zero, a finite nonzero value and infinite respectively. Strictly proper and bi-proper systems may be generally recalled as proper. 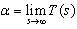 Lemma1: An observable state space realization of a singular system is impulse free, if and only if, its transfer function has a nonnegative relative degree. (i.e. it is proper)Proof: The transfer function matrix from input to state for system (1) can be computed as:
Lemma1: An observable state space realization of a singular system is impulse free, if and only if, its transfer function has a nonnegative relative degree. (i.e. it is proper)Proof: The transfer function matrix from input to state for system (1) can be computed as: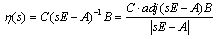 It is known that degree of the nominator is equal to rank of E at most, therefore, if condition (2) is satisfied then the system transfer matrix will be proper. On the other hand if transfer matrix is not proper condition (2) is certainly not satisfied. Remark2: The observability assumption is essential for the above lemma because it can be easily shown that it may be a number of unobservable impulsive modes which do not appear in the output. Also note that condition (2) is a general condition for impulse free systems but in order to compare it to corollary 1, the observability assumption is needed. Lemma2: In the unity output feedback structure the closed loop system is strictly proper if the compensator/plant combination is strictly proper. Proof: Expand the nominator and denominator by their respective Taylor series.
It is known that degree of the nominator is equal to rank of E at most, therefore, if condition (2) is satisfied then the system transfer matrix will be proper. On the other hand if transfer matrix is not proper condition (2) is certainly not satisfied. Remark2: The observability assumption is essential for the above lemma because it can be easily shown that it may be a number of unobservable impulsive modes which do not appear in the output. Also note that condition (2) is a general condition for impulse free systems but in order to compare it to corollary 1, the observability assumption is needed. Lemma2: In the unity output feedback structure the closed loop system is strictly proper if the compensator/plant combination is strictly proper. Proof: Expand the nominator and denominator by their respective Taylor series. 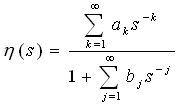 Because CP is supposed to be strictly proper, the largest term in its expansion has a negative power, therefore the denominator has a greater degree than the nominator and thus the closed loop system is strictly proper.
Because CP is supposed to be strictly proper, the largest term in its expansion has a negative power, therefore the denominator has a greater degree than the nominator and thus the closed loop system is strictly proper. 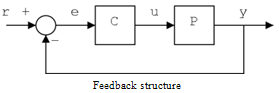 Remark3: Note that Lemma2 provides a sufficient condition. The necessary and sufficient condition is derived later. Lemma2 shows that why the objective of properness has not been considered before the introduction of descriptor systems. Assuming strictly proper functions for plant and compensator, it is trivial that the closed loop system is strictly proper. Also for a strictly proper plant and a bi-proper compensator the closed loop will be bi-proper. Lemma3: For a bi-proper plant and a bi-proper compensator, the closed loop will be improper, if and only if:
Remark3: Note that Lemma2 provides a sufficient condition. The necessary and sufficient condition is derived later. Lemma2 shows that why the objective of properness has not been considered before the introduction of descriptor systems. Assuming strictly proper functions for plant and compensator, it is trivial that the closed loop system is strictly proper. Also for a strictly proper plant and a bi-proper compensator the closed loop will be bi-proper. Lemma3: For a bi-proper plant and a bi-proper compensator, the closed loop will be improper, if and only if: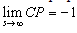 Lemma4: In order to have a strictly proper closed loop system with a unit feedback, if the plant is improper the compensator should be strictly proper with a sufficiently large relative degree. Proof: According to lemma2, for the closed loop to be strictly proper, the compensator/plant should be strictly proper. Therefore, the compensator should be strictly proper.
Lemma4: In order to have a strictly proper closed loop system with a unit feedback, if the plant is improper the compensator should be strictly proper with a sufficiently large relative degree. Proof: According to lemma2, for the closed loop to be strictly proper, the compensator/plant should be strictly proper. Therefore, the compensator should be strictly proper.
2.2. Robust Internal Model Control of Singular Systems
In IMC structure internal model is inevitably proper or strictly proper. Therefore, there always exists a mismatch between the plant and that of the model. For a continuous output especially in case of initial jumps of the input, it is required that the plant and the internal model have the same infinite gain and the compensator is strictly proper. This issue can be treated by a smoothing pre-filter for reference signal, however by introducing such filter the method is not any robust against model uncertainties. The IMC filter is conventionally used to enhance robustness properties by penalizing the closed loop response and making the compensator implementable (i.e. proper).Moreover, it accounts for online adaptation of the control system by adjusting the filter time constant. In this paper we extend this approach by using a second IMC filter which assures the closed loop to be strictly proper and has a smooth response by compensating the singular plant impulsive behavior. The singular internal model control filter or SIMC filter is designed to yield a continuous smooth response and a robust IMC design for singular systems. In fact by using a strictly proper model in parallel to IMC, the uncertainty will become unbounded and the robust control will not be feasible any more. Therefore, the SIMC filter has another role of bounding the uncertainty profile and making the robust control problem feasible. The disk-type uncertainty profile is usually assumed in robust control schemes, which is described by the followingrelation. 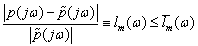 | (4) |
This uncertainty description allows us to incorporate several singular systems in the design, while the state space uncertainty descriptions are limited to represent only singular systems with a pre-specified singularity index. If one augments the improper plant by high frequency stable poles a strictly proper model can be obtained, which has a very close behavior to plant at least at low enough frequency range. Larger poles result in a closer response to that of the plant in wider bandwidths. However, in this way the uncertainty becomes unbounded. In particular assume a polynomial of stable real poles with a unit steady state gain namely D, then one can write: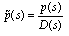 | (5) |
The above description for model is the most natural selection for a strictly proper model, whose behaviour is as close as that of the plant. However, in this situation the mismatch between plant and model is not included in a disk shaped region. In other words the uncertainty bound will be infinity. Now we can take different approaches: Choose another internal model which yields bounded uncertainty; developing new theory for this kind of uncertainty; or modify the plant input in order to bind the uncertainty as well as removing impulses from the response. The following lemmas are introductory materials for the theorems developed later in this paper.Lemma5: A control system is robustly stale, if and only if, the complementary sensitivity function fulfils the following inequality:[12]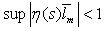 | (6) |
Remark4: For IMC structure the complementary sensitivity function and the uncertainty can be computed as follows: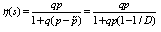 | (7) |
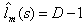 | (8) |
Therefore, in this case condition (6) cannot be satisfied. Thus we need to modify the IMC structure or algorithm in order to gain a more tractable uncertainty profile. In the following section the SIMC filter is introduced and the proposed method is studied.
3. The SIMC Filter
The idea of augmenting the IMC compensator by an IMC filter can be extended to singular systems in a different manner. According to the previousdiscussions one way to overcome the obstacles in IMC of singular systems is to augment the compensator by an additional IMC filter, we call it SIMC. This filter have the same structure as the conventional IMC filter for step reference signals, and therefore, the IMC problem of singular systems consists of finding two time constants; One for the conventional IMC which adjusts the closed loop performance, robustness and noise amplification; and one for the feasibility of robust control and impulse elimination of the singular plant. It is expected that for a singular system more parameters are required to be controlled, because a singular system is a general form of a linear system and cannot be treated by the same existing methods in standard form. One advantage of SIMC is to solve the problem by introducing an additional filter without any need of complicated design procedures. Define the SIMC filter as a low pass filter as follows.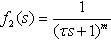 | (9) |
Lemma6: Define SIMC filter as stated in (9), therefore the closed loop system is strictly proper, if and only if: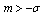 | (10) |
In which, parameter σ denotes the relative degree of the plant. Proof: Using (9-10) as the SIMC filter, the relative degree of plant/compensator becomes strictly proper. Therefore, by means of lemma2, the closed loop system is strictly proper. Remark5: There is no need to introduce pole zero cancellation issues, because SIMC filter cancels minimum-phase zeros of the plant.Lemma7: Together with SIMC filter the singular plant is capable of being robustly controlled, if (6) can be satisfied. Proof: The new uncertainty profile have the following shape: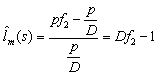 | (11) |
Now it is easy to choose SIMC filter such that the uncertainty profile is bounded. Remark6: Note that the real uncertainty profile between actual plant and assumed singular model is unchanged. SIMC manipulates only the mismatch between singular model and the implemented parallel strictly proper model of IMC.Also note that 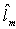 represents the uncertainty caused by singular system while
represents the uncertainty caused by singular system while 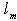 is the actual uncertainty.Lemma8: The closed loop system with SIMC structure characterized by equations (9-11) is robustly stable, if and only if:
is the actual uncertainty.Lemma8: The closed loop system with SIMC structure characterized by equations (9-11) is robustly stable, if and only if: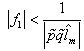 | (12) |
Proof: The complementary sensitivity function can be stated as: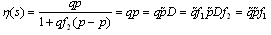 Therefore condition (6) can be states as in (12). Remark7: The above lemma states an essential character of SIMC, the SIMC filter caused the uncertainty to remain in a disk shaped region and the robust stability criterion is then applicable to the problem. If one studies condition (6) with and without SIMC filter, it can be seen that thos filter imposes a bound on the uncertainty. Also choosing D as the inverse of SIMC filter, the uncertainty profile remains unchanged and the uncertainty caused by singular system will be zero as can be seen from (11). When there are some model inaccuracies or disturbances, condition (12) cannot be met easily because a specific performance index is expected in the control objectives. In these situations a natural compromise exists and the penalizing the performance is inevitable. Note that one can set the IMC filter to zero in order to satisfy (12) but this means open loop control of the system, and therefore, losing performance. The uncertainty bound generally increases at higher frequencies. A natural routine for making the controller robust is to design a nominal H2-optimal controller according to performance specifications and then increasing the filter time constant to meet the desired robustness properties. Theorem1: Assuming
Therefore condition (6) can be states as in (12). Remark7: The above lemma states an essential character of SIMC, the SIMC filter caused the uncertainty to remain in a disk shaped region and the robust stability criterion is then applicable to the problem. If one studies condition (6) with and without SIMC filter, it can be seen that thos filter imposes a bound on the uncertainty. Also choosing D as the inverse of SIMC filter, the uncertainty profile remains unchanged and the uncertainty caused by singular system will be zero as can be seen from (11). When there are some model inaccuracies or disturbances, condition (12) cannot be met easily because a specific performance index is expected in the control objectives. In these situations a natural compromise exists and the penalizing the performance is inevitable. Note that one can set the IMC filter to zero in order to satisfy (12) but this means open loop control of the system, and therefore, losing performance. The uncertainty bound generally increases at higher frequencies. A natural routine for making the controller robust is to design a nominal H2-optimal controller according to performance specifications and then increasing the filter time constant to meet the desired robustness properties. Theorem1: Assuming 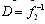 then there exists an IMC filter such that the closed loop system is robustly stable, and furthermore, the system exhibits robust performance at zero frequency, if and only if:
then there exists an IMC filter such that the closed loop system is robustly stable, and furthermore, the system exhibits robust performance at zero frequency, if and only if: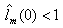 | (13) |
Proof: The IMC filter should satisfy (12) for robust stability, because of the structure selected for IMC filter, the maximum value for the filter is unity and it occurs at zero frequency. Therefore, for the nominal plant (12) can be satisfied only if the uncertainty upper bound is smaller than unity, and therefore, the necessary condition for existence of such IMC filter is (13). The proof of sufficiency follows immediately from the above condition. Remark8: Note that theorem 1 is an extension of the existing result in standard systems. Although the SIMC filter does not appear explicitly in the theorem, it has an essential role in the derivation of the theorem as well as the lemmas. In other words introducing SIMC makes it possible to apply the existing framework for robust control to singular systems. Remark9: Theorem1 just considers the solvability of (12). In other words it studies the existence of an appropriate IMC filter which solves the robust control problem. In order to find such IMC filter one should increase the time constant and check that the robust stability criterion is satisfied. Remark10: It should be noticed that there exists no constraint on the SIMC filter time constant and any positive time constant can be chosen for this filter. However when smoothness of the response is also a requirement, large time constant is required, and when a fast response is desired, it is better to choose the time constant as small as possible. Note that if the SIMC filter time constant is larger than that of IMC filter and the plant dominant time constant, this will dominate the closed loop time constant. In fact the closed loop time constant is the largest time constant among the plant, IMC filter and SIMC filter time constants. Because of robustness considerations SIMC filter time constant may be smaller than that of IMC filter, and therefore, it does not restrict the closed loop performance. It is not possible to decrease SIMC filter time constant as much as desired, since input noises may be amplified. Remark11: Note that (13) means that steady state gains for the plant and model should have the same sign. A little mismatch between plant and model steady state gain may cause instability if their signs are different. This a common drawback of robust control systems for plants with zeros near the origin. By a slight change of the zero location the closed loop may become unstable if the zero is near the origin.Lemma8: The irregularity of closed loop occurs, if and only if: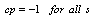 Proof: From the definition of regularity, a singular system is irregular if and only if:
Proof: From the definition of regularity, a singular system is irregular if and only if: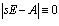 | (14) |
In the frequency domain context of output feedback control systems the above determinant is the characteristic polynomial of system or the denominator of complementary sensitivity function. Write the closed loop transfer function as: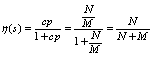 According to (14) and (15) the closed loop system is irregular, if and only if:
According to (14) and (15) the closed loop system is irregular, if and only if: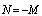 which, can be rewritten as:
which, can be rewritten as: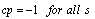 | (15) |
The last equality also means an unsolvable algebraic loop in the simulation. Corollary2: For a strictly proper plant/compensator, (15) does not occur because polynomial (16) is never zero.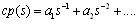 | (16) |
As a result for a strictly proper compensator/plant combination the regularity issue will not occur. This corollary depicts the fact that why the regularity control objective is introduced only for singular systems and not for standard strictly proper ones. In the following theorem we may introduce the significant characteristics of the proposed algorithm.Theorem2: The closed loop system with an appropriate IMC filter designed according to (12) is robustly strictly proper and robustly regular for all uncertainties described by (4).Proof: Note that from theorem1, the closed loop robust stability and zero frequency performance are assured. The family of plants described by (4) have all a singularity index smaller than or equal to that of nominal plant. This can be shown as follows; assume that there is a plant in the family (4) that has a larger singularity index than the nominal plant. Then uncertainty profile can be written as: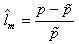 From the above assumption uncertainty will increase by frequency because it has an improper transfer function. Therefore, (4) cannot be satisfied as the uncertainty is unbounded. Moreover, for any plant being in family (4) the relative degree of SIMC filter is greater than or equal to the plant singularity index and thus the closed loop system is robustly strictly proper according to lemma2. Also note that regularity of the plant is guaranteed by lemma8 because of strict properness of plant/compensator combination.The following design procedure can be followed for robust internal model control of a singular plant. Design Procedure: A. Choose the polynomial D and set f2 as its inverse. The polynomial time constant should be smaller than the dominant time constant of plant. According to nominal singular plant choose m such that the strictly properness of closed loop is guaranteed. B. For the nominal plant check the feasibility of robust control having uncertainty profile as (4) according to (12), if this is satisfied, design IMC filter for a good performance in nominal case. C. Redesign SIMC filter for having better performance if it is required. D. Simulation ResultsSimulation of an improper system is not possible with the existing numerical methods, since simulation needs future data for computing the present state vector. This` is why many papers in the field of singular systems do not include any simulation examples or just simulate causal singular systems. However, if the closed loop system is proper, any simulationsoftware can easily implement the closed loop system regardless of the inner unsolvable loops, which form singular systems in the inner parts of the closed loop system.In this paper, some illustrative but simple examples are chosen in order to show the effectiveness of the proposed algorithm. Example1: Consider the nonlinear system described by the following equations:
From the above assumption uncertainty will increase by frequency because it has an improper transfer function. Therefore, (4) cannot be satisfied as the uncertainty is unbounded. Moreover, for any plant being in family (4) the relative degree of SIMC filter is greater than or equal to the plant singularity index and thus the closed loop system is robustly strictly proper according to lemma2. Also note that regularity of the plant is guaranteed by lemma8 because of strict properness of plant/compensator combination.The following design procedure can be followed for robust internal model control of a singular plant. Design Procedure: A. Choose the polynomial D and set f2 as its inverse. The polynomial time constant should be smaller than the dominant time constant of plant. According to nominal singular plant choose m such that the strictly properness of closed loop is guaranteed. B. For the nominal plant check the feasibility of robust control having uncertainty profile as (4) according to (12), if this is satisfied, design IMC filter for a good performance in nominal case. C. Redesign SIMC filter for having better performance if it is required. D. Simulation ResultsSimulation of an improper system is not possible with the existing numerical methods, since simulation needs future data for computing the present state vector. This` is why many papers in the field of singular systems do not include any simulation examples or just simulate causal singular systems. However, if the closed loop system is proper, any simulationsoftware can easily implement the closed loop system regardless of the inner unsolvable loops, which form singular systems in the inner parts of the closed loop system.In this paper, some illustrative but simple examples are chosen in order to show the effectiveness of the proposed algorithm. Example1: Consider the nonlinear system described by the following equations: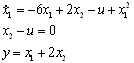 | (17) |
The latter output equation describes the simplest form of output equation. Nonlinear output may occur in a singular system, and can treated the same way as in here. The algebraic part of a singular system denotes its limitations for having arbitrary initial conditions. The system described by (17) can be modelled as a standard state space system, too. For a nominal input of u=9, the equilibrium point is: 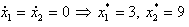 | (18) |
In case of nonlinear term in (17), the nonlinearity can be considered as an uncertainty, and not included in the linear model representation. The process model may be considered as a bi-proper transfer function.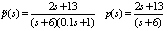 The compensator, IMC and SIMC filters may be chosen as:
The compensator, IMC and SIMC filters may be chosen as: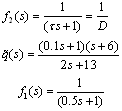 The closed loop system responses to different inputs with different initial conditions are shown in figures 1 to 3. As it is seen in these figures, before and after the abrupt change in the set point, initial condition response is vanished and then the set point signal is tracked without any offset. Disturbance rejection is also well performed as seen in these figure, and the stability of the closed loop system is well illustrated in the phase portraits given in figure 4 for different initial conditions.
The closed loop system responses to different inputs with different initial conditions are shown in figures 1 to 3. As it is seen in these figures, before and after the abrupt change in the set point, initial condition response is vanished and then the set point signal is tracked without any offset. Disturbance rejection is also well performed as seen in these figure, and the stability of the closed loop system is well illustrated in the phase portraits given in figure 4 for different initial conditions.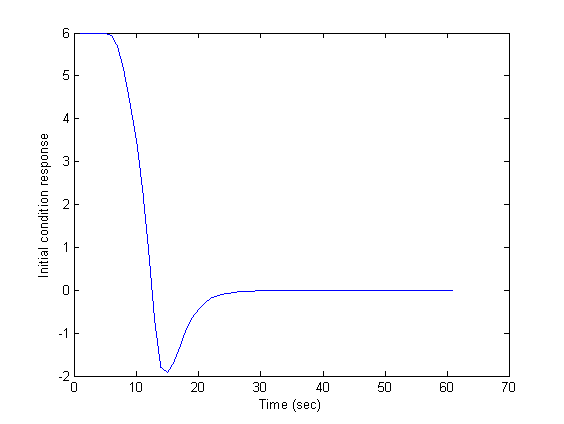 | Figure 1. System response to initial condition |
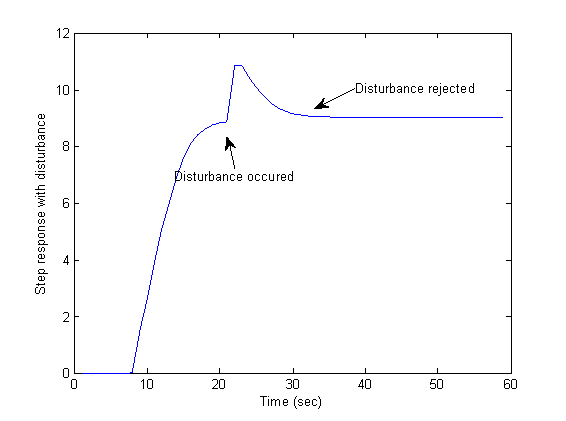 | Figure 2. Set point and disturbance response |
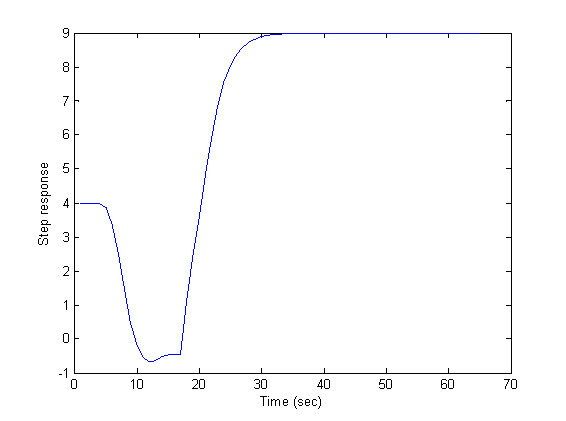 | Figure 3. Set point response with initial condition |
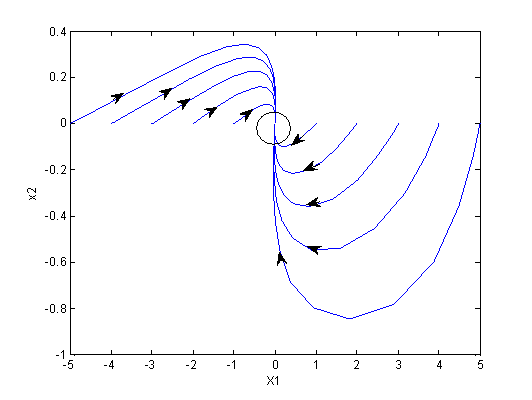 | Figure 4. phase portrait of closed loop near the origin |
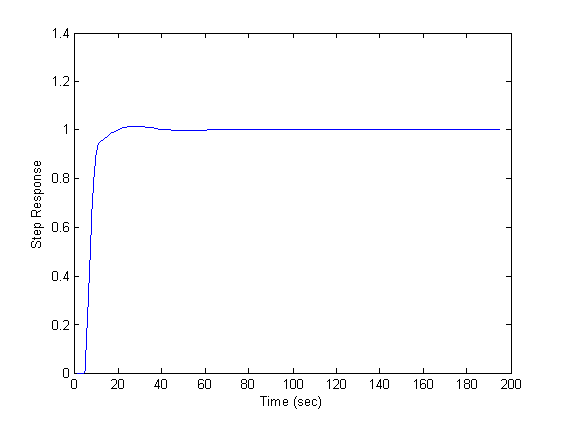 | Figure 5. step response for p1 |
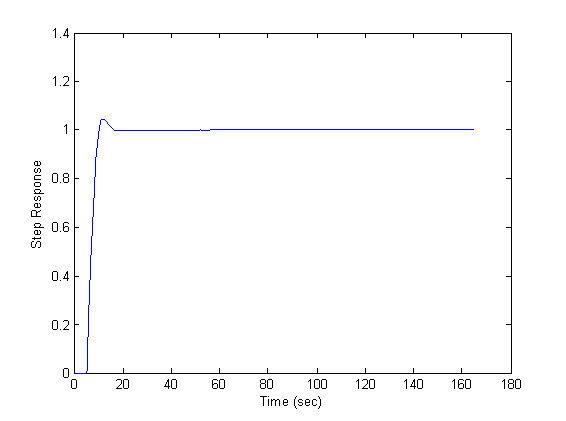 | Figure 6. Step response for p2 |
This example shows that the closed loop system is strictly proper regardless of any bounded model uncertainties. Moreover, it provides an example of robust stability and zero frequency performance design. Example2: Consider a group of linear singular systems as described by the following set of transfer function. 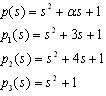 And assume that the nominal plant (model) is as follows.
And assume that the nominal plant (model) is as follows.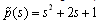 The parallel model and compensator are selected as:
The parallel model and compensator are selected as: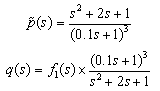 The uncertainty norm is bounded for all of the models described in (19), however, its infinity norm is near the unity for case of p4. Following figures depict closed loop behavior in tracking step set point. As the uncertainty bound increases, the system response is deteriorated in terms of both performance and stability margin. In the last case the oscillating behavior of plant is not included in the model and therefore closed loop response is not satisfactory. Note that while steady state gains of plant and model have the same sign, the closed loop is robustly stable, and while the uncertainty is bounded it is robustly strictly proper. This example shows that even for such wide uncertainty spectrum the proposed method is able to stabilize the system, while at the cases where the stability conditions are close to be deteriorated, the performance of the system becomes oscillatory.
The uncertainty norm is bounded for all of the models described in (19), however, its infinity norm is near the unity for case of p4. Following figures depict closed loop behavior in tracking step set point. As the uncertainty bound increases, the system response is deteriorated in terms of both performance and stability margin. In the last case the oscillating behavior of plant is not included in the model and therefore closed loop response is not satisfactory. Note that while steady state gains of plant and model have the same sign, the closed loop is robustly stable, and while the uncertainty is bounded it is robustly strictly proper. This example shows that even for such wide uncertainty spectrum the proposed method is able to stabilize the system, while at the cases where the stability conditions are close to be deteriorated, the performance of the system becomes oscillatory.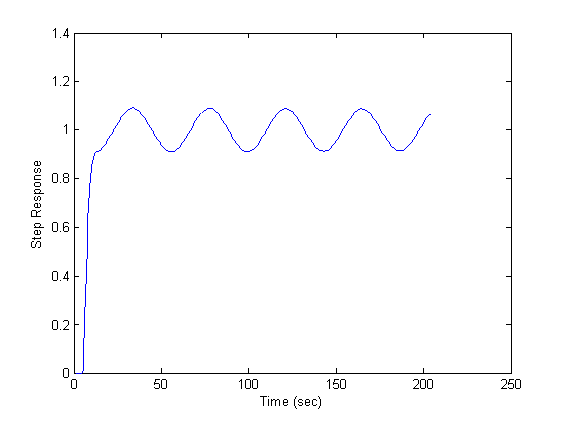 | Figure 7. Step response for p3 |
4. Conclusions
In this paper an effective and simple control scheme is proposed for robust internal model control of singular linear systems. The method has many advantages over the existing, state space methods including robust strict properness of the closed loop, avoiding algebraic loops, robust tracking of specific signals and the ability to robustly stabilize a larger group of singular systems comparing to that of other methods. Two simulation examples are included to depict the algorithm performance. It is shown that robust stability of the closed loop system is preserved in the presence of large uncertainty spectrum, provided that the stability conditions provided in this paper is satisfied.
References
| [1] | Mertzios, B. G. and F. Lewis, “Fundamental matrix of discrete singular systems”, Journal of circuits, systems and signal processing, vol.8, NO.3, 1989 |
| [2] | Dai, L. “Singular control systems”, Springer verlag, 1989 |
| [3] | Campbell, S. L, R. Nikoukhah and B. C. Levy, “Kalman filtering for general discrete time linear systems”, IEEE transactions on automatic control, vol.44, NO.10, pp. 1829-1839,1999 |
| [4] | Luenberger, D. “Dynamic equations in descriptor form”, IEEE transactions on automatc control, vol.AC.22, NO.3, June, 1977 |
| [5] | Syrmos, V. L. and F. L. Lewis, “Robust eigen value assignment in generalized systems”Proceedings of the 30th conference on decision and control, England, 1991 |
| [6] | Fang, C. H., L. Lee and F. R. Chang, “Robust control analysis and design for discrete time singular systems”, Automatica, Vol.30, NO.11, pp.1741-1750, 1994 |
| [7] | Xu, S. , C. Yang, Y. Neu and J. Lam, “Robust stabilization for uncertain discrete singular systems”, Automatica, Vol.37, pp.769-774, 2001 |
| [8] | Mukundan, R. and W. Dayawansa, “Feedback control of singular systems- proportional and derivative feedback of the state”, International journal of systems science, vol.14, NO.6, pp.615-632, 1983 |
| [9] | Chu, D. L., H. C. Chan and D. W. Ho, “Regularization of singular systems by derivative and proportional output feedback”, Siam journal of matrix nalysis and applications, vol.19, NO.1, pp.21-38, January, 1998 |
| [10] | Xu, S. and J. Lam, ”Robust stability and stabilization of discrete singular systems: An equivalent characterization”, IEEE transaction on automatic control, vol.49, NO.4, April 2004 |
| [11] | Hou, M. “Controllability and elimination of impulsivemodes in descriptor systems”, IEEE transactions on automatic control, vol.49, NO.10, 2004 |
| [12] | Morari, M. and E. Zafiriou, “Robust process control”, Prentice Hall, 1989 |
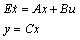
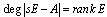
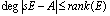
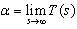 Lemma1: An observable state space realization of a singular system is impulse free, if and only if, its transfer function has a nonnegative relative degree. (i.e. it is proper)Proof: The transfer function matrix from input to state for system (1) can be computed as:
Lemma1: An observable state space realization of a singular system is impulse free, if and only if, its transfer function has a nonnegative relative degree. (i.e. it is proper)Proof: The transfer function matrix from input to state for system (1) can be computed as: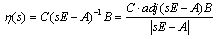 It is known that degree of the nominator is equal to rank of E at most, therefore, if condition (2) is satisfied then the system transfer matrix will be proper. On the other hand if transfer matrix is not proper condition (2) is certainly not satisfied. Remark2: The observability assumption is essential for the above lemma because it can be easily shown that it may be a number of unobservable impulsive modes which do not appear in the output. Also note that condition (2) is a general condition for impulse free systems but in order to compare it to corollary 1, the observability assumption is needed. Lemma2: In the unity output feedback structure the closed loop system is strictly proper if the compensator/plant combination is strictly proper. Proof: Expand the nominator and denominator by their respective Taylor series.
It is known that degree of the nominator is equal to rank of E at most, therefore, if condition (2) is satisfied then the system transfer matrix will be proper. On the other hand if transfer matrix is not proper condition (2) is certainly not satisfied. Remark2: The observability assumption is essential for the above lemma because it can be easily shown that it may be a number of unobservable impulsive modes which do not appear in the output. Also note that condition (2) is a general condition for impulse free systems but in order to compare it to corollary 1, the observability assumption is needed. Lemma2: In the unity output feedback structure the closed loop system is strictly proper if the compensator/plant combination is strictly proper. Proof: Expand the nominator and denominator by their respective Taylor series. 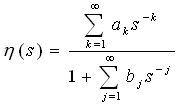 Because CP is supposed to be strictly proper, the largest term in its expansion has a negative power, therefore the denominator has a greater degree than the nominator and thus the closed loop system is strictly proper.
Because CP is supposed to be strictly proper, the largest term in its expansion has a negative power, therefore the denominator has a greater degree than the nominator and thus the closed loop system is strictly proper.  Remark3: Note that Lemma2 provides a sufficient condition. The necessary and sufficient condition is derived later. Lemma2 shows that why the objective of properness has not been considered before the introduction of descriptor systems. Assuming strictly proper functions for plant and compensator, it is trivial that the closed loop system is strictly proper. Also for a strictly proper plant and a bi-proper compensator the closed loop will be bi-proper. Lemma3: For a bi-proper plant and a bi-proper compensator, the closed loop will be improper, if and only if:
Remark3: Note that Lemma2 provides a sufficient condition. The necessary and sufficient condition is derived later. Lemma2 shows that why the objective of properness has not been considered before the introduction of descriptor systems. Assuming strictly proper functions for plant and compensator, it is trivial that the closed loop system is strictly proper. Also for a strictly proper plant and a bi-proper compensator the closed loop will be bi-proper. Lemma3: For a bi-proper plant and a bi-proper compensator, the closed loop will be improper, if and only if: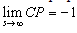 Lemma4: In order to have a strictly proper closed loop system with a unit feedback, if the plant is improper the compensator should be strictly proper with a sufficiently large relative degree. Proof: According to lemma2, for the closed loop to be strictly proper, the compensator/plant should be strictly proper. Therefore, the compensator should be strictly proper.
Lemma4: In order to have a strictly proper closed loop system with a unit feedback, if the plant is improper the compensator should be strictly proper with a sufficiently large relative degree. Proof: According to lemma2, for the closed loop to be strictly proper, the compensator/plant should be strictly proper. Therefore, the compensator should be strictly proper. 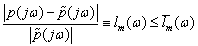
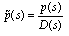
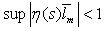
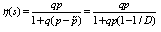
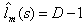
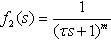
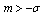
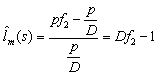
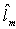 represents the uncertainty caused by singular system while
represents the uncertainty caused by singular system while 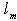 is the actual uncertainty.Lemma8: The closed loop system with SIMC structure characterized by equations (9-11) is robustly stable, if and only if:
is the actual uncertainty.Lemma8: The closed loop system with SIMC structure characterized by equations (9-11) is robustly stable, if and only if: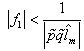
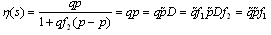 Therefore condition (6) can be states as in (12). Remark7: The above lemma states an essential character of SIMC, the SIMC filter caused the uncertainty to remain in a disk shaped region and the robust stability criterion is then applicable to the problem. If one studies condition (6) with and without SIMC filter, it can be seen that thos filter imposes a bound on the uncertainty. Also choosing D as the inverse of SIMC filter, the uncertainty profile remains unchanged and the uncertainty caused by singular system will be zero as can be seen from (11). When there are some model inaccuracies or disturbances, condition (12) cannot be met easily because a specific performance index is expected in the control objectives. In these situations a natural compromise exists and the penalizing the performance is inevitable. Note that one can set the IMC filter to zero in order to satisfy (12) but this means open loop control of the system, and therefore, losing performance. The uncertainty bound generally increases at higher frequencies. A natural routine for making the controller robust is to design a nominal H2-optimal controller according to performance specifications and then increasing the filter time constant to meet the desired robustness properties. Theorem1: Assuming
Therefore condition (6) can be states as in (12). Remark7: The above lemma states an essential character of SIMC, the SIMC filter caused the uncertainty to remain in a disk shaped region and the robust stability criterion is then applicable to the problem. If one studies condition (6) with and without SIMC filter, it can be seen that thos filter imposes a bound on the uncertainty. Also choosing D as the inverse of SIMC filter, the uncertainty profile remains unchanged and the uncertainty caused by singular system will be zero as can be seen from (11). When there are some model inaccuracies or disturbances, condition (12) cannot be met easily because a specific performance index is expected in the control objectives. In these situations a natural compromise exists and the penalizing the performance is inevitable. Note that one can set the IMC filter to zero in order to satisfy (12) but this means open loop control of the system, and therefore, losing performance. The uncertainty bound generally increases at higher frequencies. A natural routine for making the controller robust is to design a nominal H2-optimal controller according to performance specifications and then increasing the filter time constant to meet the desired robustness properties. Theorem1: Assuming 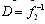 then there exists an IMC filter such that the closed loop system is robustly stable, and furthermore, the system exhibits robust performance at zero frequency, if and only if:
then there exists an IMC filter such that the closed loop system is robustly stable, and furthermore, the system exhibits robust performance at zero frequency, if and only if: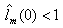
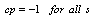 Proof: From the definition of regularity, a singular system is irregular if and only if:
Proof: From the definition of regularity, a singular system is irregular if and only if: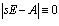
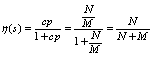 According to (14) and (15) the closed loop system is irregular, if and only if:
According to (14) and (15) the closed loop system is irregular, if and only if: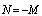 which, can be rewritten as:
which, can be rewritten as: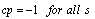
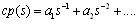
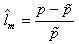 From the above assumption uncertainty will increase by frequency because it has an improper transfer function. Therefore, (4) cannot be satisfied as the uncertainty is unbounded. Moreover, for any plant being in family (4) the relative degree of SIMC filter is greater than or equal to the plant singularity index and thus the closed loop system is robustly strictly proper according to lemma2. Also note that regularity of the plant is guaranteed by lemma8 because of strict properness of plant/compensator combination.The following design procedure can be followed for robust internal model control of a singular plant. Design Procedure: A. Choose the polynomial D and set f2 as its inverse. The polynomial time constant should be smaller than the dominant time constant of plant. According to nominal singular plant choose m such that the strictly properness of closed loop is guaranteed. B. For the nominal plant check the feasibility of robust control having uncertainty profile as (4) according to (12), if this is satisfied, design IMC filter for a good performance in nominal case. C. Redesign SIMC filter for having better performance if it is required. D. Simulation ResultsSimulation of an improper system is not possible with the existing numerical methods, since simulation needs future data for computing the present state vector. This` is why many papers in the field of singular systems do not include any simulation examples or just simulate causal singular systems. However, if the closed loop system is proper, any simulationsoftware can easily implement the closed loop system regardless of the inner unsolvable loops, which form singular systems in the inner parts of the closed loop system.In this paper, some illustrative but simple examples are chosen in order to show the effectiveness of the proposed algorithm. Example1: Consider the nonlinear system described by the following equations:
From the above assumption uncertainty will increase by frequency because it has an improper transfer function. Therefore, (4) cannot be satisfied as the uncertainty is unbounded. Moreover, for any plant being in family (4) the relative degree of SIMC filter is greater than or equal to the plant singularity index and thus the closed loop system is robustly strictly proper according to lemma2. Also note that regularity of the plant is guaranteed by lemma8 because of strict properness of plant/compensator combination.The following design procedure can be followed for robust internal model control of a singular plant. Design Procedure: A. Choose the polynomial D and set f2 as its inverse. The polynomial time constant should be smaller than the dominant time constant of plant. According to nominal singular plant choose m such that the strictly properness of closed loop is guaranteed. B. For the nominal plant check the feasibility of robust control having uncertainty profile as (4) according to (12), if this is satisfied, design IMC filter for a good performance in nominal case. C. Redesign SIMC filter for having better performance if it is required. D. Simulation ResultsSimulation of an improper system is not possible with the existing numerical methods, since simulation needs future data for computing the present state vector. This` is why many papers in the field of singular systems do not include any simulation examples or just simulate causal singular systems. However, if the closed loop system is proper, any simulationsoftware can easily implement the closed loop system regardless of the inner unsolvable loops, which form singular systems in the inner parts of the closed loop system.In this paper, some illustrative but simple examples are chosen in order to show the effectiveness of the proposed algorithm. Example1: Consider the nonlinear system described by the following equations: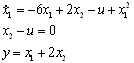
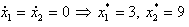
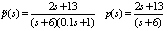 The compensator, IMC and SIMC filters may be chosen as:
The compensator, IMC and SIMC filters may be chosen as: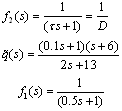 The closed loop system responses to different inputs with different initial conditions are shown in figures 1 to 3. As it is seen in these figures, before and after the abrupt change in the set point, initial condition response is vanished and then the set point signal is tracked without any offset. Disturbance rejection is also well performed as seen in these figure, and the stability of the closed loop system is well illustrated in the phase portraits given in figure 4 for different initial conditions.
The closed loop system responses to different inputs with different initial conditions are shown in figures 1 to 3. As it is seen in these figures, before and after the abrupt change in the set point, initial condition response is vanished and then the set point signal is tracked without any offset. Disturbance rejection is also well performed as seen in these figure, and the stability of the closed loop system is well illustrated in the phase portraits given in figure 4 for different initial conditions.





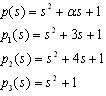 And assume that the nominal plant (model) is as follows.
And assume that the nominal plant (model) is as follows.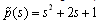 The parallel model and compensator are selected as:
The parallel model and compensator are selected as: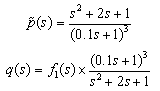 The uncertainty norm is bounded for all of the models described in (19), however, its infinity norm is near the unity for case of p4. Following figures depict closed loop behavior in tracking step set point. As the uncertainty bound increases, the system response is deteriorated in terms of both performance and stability margin. In the last case the oscillating behavior of plant is not included in the model and therefore closed loop response is not satisfactory. Note that while steady state gains of plant and model have the same sign, the closed loop is robustly stable, and while the uncertainty is bounded it is robustly strictly proper. This example shows that even for such wide uncertainty spectrum the proposed method is able to stabilize the system, while at the cases where the stability conditions are close to be deteriorated, the performance of the system becomes oscillatory.
The uncertainty norm is bounded for all of the models described in (19), however, its infinity norm is near the unity for case of p4. Following figures depict closed loop behavior in tracking step set point. As the uncertainty bound increases, the system response is deteriorated in terms of both performance and stability margin. In the last case the oscillating behavior of plant is not included in the model and therefore closed loop response is not satisfactory. Note that while steady state gains of plant and model have the same sign, the closed loop is robustly stable, and while the uncertainty is bounded it is robustly strictly proper. This example shows that even for such wide uncertainty spectrum the proposed method is able to stabilize the system, while at the cases where the stability conditions are close to be deteriorated, the performance of the system becomes oscillatory.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML