Obaidur Rahaman
European University of Bangladesh, Department of Computer Science and Engineering, Bangladesh
Correspondence to: Obaidur Rahaman, European University of Bangladesh, Department of Computer Science and Engineering, Bangladesh.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Data and Information Security has become very important in today’s modern world, as a result of these various methods are adopted to bypass it. With the advent of the internet, security has became a major concern and the history of security allows a better understanding of the emergence of security technology. The internet structure itself allowed for many security threats to occur. The mechanism of the internet, when modified can reduce the possible attacks that can be sent across the network. By knowing the attack methods, allows for the appropriate security to emerge. Many modern spare secure themselves from the internet by means of Elliptic Curve Cryptography, Text Encryption and Decryption process and Card Shuffling Process. It provides higher level of security with lesser key size compared to other Cryptographic techniques. A new technique has been proposed in this paper where the classic technique of mapping the characters to affine points in the elliptic curve has been removed. The corresponding ASCII values of the plain text are paired up. The paired values serve as input for the Elliptic curve cryptography. This new technique has been avoided for the costly operation of mapping and the need to share the common lookup table between the sender and the receiver. The algorithm is designed in such a way that it can be used to encrypt or decrypt any type of script with defined ASCII values.
Keywords:
Cryptography, Elliptic curve cryptography, Encryption and Decryption Process, Card Shuffling Process
Cite this paper: Obaidur Rahaman, Data and Information Security in Modern World by using Elliptic Curve Cryptography, Computer Science and Engineering, Vol. 7 No. 2, 2017, pp. 29-44. doi: 10.5923/j.computer.20170702.01.
1. Introduction
Data and Information security is one of the most important issues in the modern civilization. In this modern world most of the data are transferred and stored by using internet. So it is important to secure our data from unauthorized access. Computer scientists are developing different types of mechanism to secure data. As old mechanisms are destroyed by different types of unauthorized attacks, computer scientists are developing new and modern types of security mechanism to protect data. Data are encrypted thus unauthorized user can’t get actual data and decrypted to use by authorized user. Cryptology is the study of secure communications, which encompasses both cryptography and cryptanalysis [1]. A strong data encryption and decryption technique is required to provide confidentiality of sensitive data from security attacks. The idea of information security leads to the evolution of Cryptography. In other words, Cryptography is the science of keeping information secure. It involves encryption and decryption of messages. There have been many known cryptographic algorithms. The crux of any cryptographic algorithm is the “seed” or the “key” used for encrypting/decrypting the information. Many of the cryptographic algorithms are available publicly, though some organizations believe in having the algorithm a secret. The general method is in using a publicly known algorithm while maintaining the key secret. We have studied application of Elliptic Curves over card shuffling logic for traditional key exchange and encryption of text. We have implemented both and proposed a scheme for encryption of images. It was partially accomplished for a small size image.
2. Implementation of Elliptic Curve Cryptography on Text and Image
Describe a brief background of encryption/decryption and key exchange are using in ECC thesis paper “Implementation of Elliptic Curve Cryptography (ECC) on Text and Image” [7]. Used C++ to implement text encryption and mapping table to map the ASCII value of Elliptic curve coordinate. Reverse mapping is used while decryption.Global Public ElementsEq(a,b) elliptic curve with parameters a, b & q in the equationY2 mod q=(X3+aX+b) mod qQ Base point on elliptic curveUser A Key GenerationSelect private key kA, kA< nCalculate public P, P=kA × QUser B Key GenerationSelect private key kB, kB< nCalculate public M, M=kB × QGeneration of Secret Key by user AP1=K=kA × MGeneration of Secret Key by user BP2=K=kB × PThe two calculations produce the same result becausekA × M = k A × (k B × Q) = k B × (k A × Q) = k B × PTo break this scheme, an attacker would be needed to be able to compute k given G & kG, which is found to be tough.For example, scalar multiple k is 5; G ≡ (2,2) then let 5G= D≡(153,108) for a=0, b=-4, q=211. Given the values of G and D, it is difficult to find out the scalar multiple k=5.
2.1. Elliptic Curve Encryption and Decryption
1. Consider a message ‘Pm’ sent from A to B. ‘A’ chooses a random positive integer ‘k’, a private key ‘n’ and generates the public key P = n × G and produces the ciphertext ‘Cm’ consisting of pair of points Cm={kG, Pm + kPB}where G is the base point selected on the Elliptic Curve, PB= nB × G is the public key of B with private key ‘nB’ 2. To decrypt the ciphertext, B multiplies the 1st point in the pair by B’s secret & subtracts the result from the 2nd point Pm + kPB - nB(kG) = Pm + k(nB G) – nB(kG)=Pm
2.2. Software Implementation
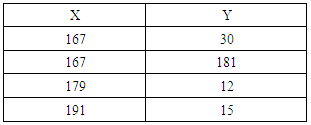
We have implemented the key exchange and the text encryption procedure using C++.a. Defining basic functions that are to be used in all programs:-Various codes under this section are:1. Code to find the multiplicative inverse of an integer for a given prime number:-For this code, we have used the extended Euclid Algorithm whereby the intermediate terms are less than the prime numbers. This prevents the intermediate terms from exceeding the corresponding prime number.For example: Consider the prime number 23 Now 6-1mod 23=4, Since, (6×4) mod 23=12. Code to generate the points on an Elliptic curve:-As there is constant need for a database of the elliptic curve points, a code to scan all Y co-ordinates that satisfy the elliptic curve equation for the given X co-ordinate has been included.Equation of the elliptic curve: y2 mod p=(x3+ax+b) mod pWhere, p is a prime number.Algorithm: Inputs: p, a, ba. Enter the input data.b. x=[0: p-1]c. For each value of x, check which values of y from 0 to (p-1) satisfies the equation. d. Display the required point.For example: p=211, a=0, b=-4Given Table (1): Elliptic curve pointsTable (1). Elliptic curve points
 |
| |
|
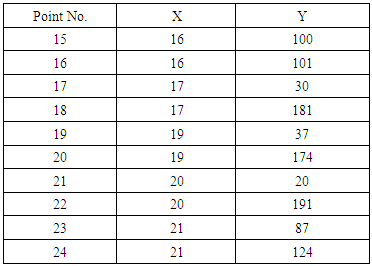
3. Code to find the public key:-Input: XG=X co-ordinate of GYG=Y co-ordinate of G nA be the private key. (A scalar multiple)Let PA be the public key. PA= nA×GWe carry out recursive addition of point G for nA times to get the point PA.For example: G= (2, 2), nA=5, (153,108) = 5(2, 2). So, PA= (153,108) is the public key for private key 5.4. Code for encoding and decoding:-a. Mapping-1 is used to convert an integer into a corresponding elliptic curve points from our database.b. Mapping-2 is used to convert an elliptic curve point into its corresponding integer from our database.c. Reverse Mapping-1 does the same function as Mapping-2.d. Reverse Mapping-2 does same function as Mapping-1.These codes perform scanning operations shown below on Table (2).For example:Table (2). Codes Scanning Operations
 |
| |
|
b. Program for secret key exchange:-The algorithm for secret key exchange is the same as in Section IV. The recursive addition used while finding the order is used to find the intermediate scalar multiple by restricting the addition at the required scalar multiplication.c. Program for text encryption:-The text encryption procedure has used the in-built feature of C++ to assign the ASCII value of a character to an integer variable when the latter is equated to the former.
2.2.1. Text Encryption Procedure
Requirement: The order of the curve (i.e. the number of points on the curve) should be greater than 126.Constraint: There should be no complete blank line in the text.1. Read a character from the plain text i.e. ‘a’.2. Gets its ASCII value into an integer variable (say I=97).3. Select the point {say E(17,30)} on the Elliptic curve corresponding to the integer I=97 as per our database. (Mapping-1).4. Now this point is encrypted as per Section V.5. Let the encrypted point be E´≡ (21,124).6. Now this point E´ is mapped once again to the database to obtain new integer. (Mapping-2).7. The new integer corresponding to E´ is I´(say 43).8. This new integer I’ is converted to data consisting of two parametersa. principle ASCII character ($) which act as an indexb. Page no. (say N=1) to which the corresponding index belongs to.9. These two parameters are sent into two different files which are transmitted.
2.2.2. Text Decryption Procedure
1. The encrypted character ($) and the corresponding page no. (N) are read from the received files.2. These two parameters are used to calculate back the integer I´.3. Then reverse mapping-2 is carried out to convert the integer I´ to a point E´ from the database.4. The point E´ is decrypted as per Section V to get a point E.5. Now reverse mapping-1 is carried out on point E to get the integer I from our database.6. The ASCII character with ASCII value I is the plain text character which was originally encrypted.
2.2.3. Features of Encryption Procedure
Generally, the encrypted curve points are transmitted on line. But in English language, certain letters have certain fixed probability of usage. So for a particular letter, if a certain elliptic curve point is transmitted always, the attacker can decrypt the elliptic curve point by checking its frequency of usage. In short, this technique has a flaw of simple substitution ciphering technique.This problem is solved by using many-to-one mapping for characters and the original characters are differentiated by using their corresponding page numbers. So, different characters may be encrypted to the same character.Solution for conversion from non-printable characters to printable character after encryption is as follows:It has been observed that the ASCII characters from 0 to 31 are non-printable. So if the encrypted character is found to be within this range, there is additional calculation which is carried out.In such a case, a tilde (~) is transmitted and the ASCII value of the encrypted character is incremented by 32 for transmission as a printable character.On the decryption side, a reverse calculation is done when a tilde (~) is detected.Result of text encryption p-decryption program:Plain textThis is document number 2 for encryption.Encrypted textG09I09I0>Eop#I^~60^p#~>IR0k0]ER0I^oR~7+~69E^DEEE~+GDecrypted textThis is document number 2 for encryption.
2.2.4. Image Encryption Procedure
The image encryption procedure is based on encrypting the intensity and thus converting it into a new intensity. This new intensity is decrypted at the receiver side to obtain the original intensity.Steps are:1. Read the intensity I from the image intensity matrix.2. Convert the intensity into an elliptic curve point E using Mapping-1.3. Encrypt the Elliptic curve point to a new point(E').4. Using Mapping-2, the new point is converted to a corresponding integer M.5. This integer M is used to calculate the new encrypted intensity I´ and page number P.
2.2.5. Image Decryption Procedure
1. The encrypted intensity I’ and the page number (P) are read from the received files.2. These 2 parameters are used to calculate the integer M.3. Using reverse mapping-2, the integer M is converted to encrypted elliptic curve point E’.4. The point E’ is decrypted to get the original point E.5. By reverse mapping-1, the original intensity I is obtained.
2.2.6. Features of Image Encryption Procedure
1. The maximum image size is 32×32 due to restriction on the number of elements in the global array.2. Any image of size greater than 32×32 needs to be cropped and sent as multiple files.3. Any image or part of it smaller than 32×32 needs to be brought to 32×32 size by padding zeros in the required locations.The procedure was implemented on Matlab images and the images were successfully encrypted and decrypted with zero error.
3. Algorithm for Text Encryption and Decryption over Elliptic Curve using Card Shuffling Logic
Many researchers implemented text encryption and decryption over elliptic curve using ASCII values or various types of mapping on common look up table. In this research work we want to introduce a playing card shuffling logic for text encryption and decryption. Card shuffling logic is used to make a dynamic and secure mapping table. We shuffle our playing cards using three randomly selected points over generated elliptic curve and use ElGamal Cryptosystem to encrypt and decrypt these points.All the procedure of the proposed algorithm is given below. Figure (1a) shows our proposed mechanism.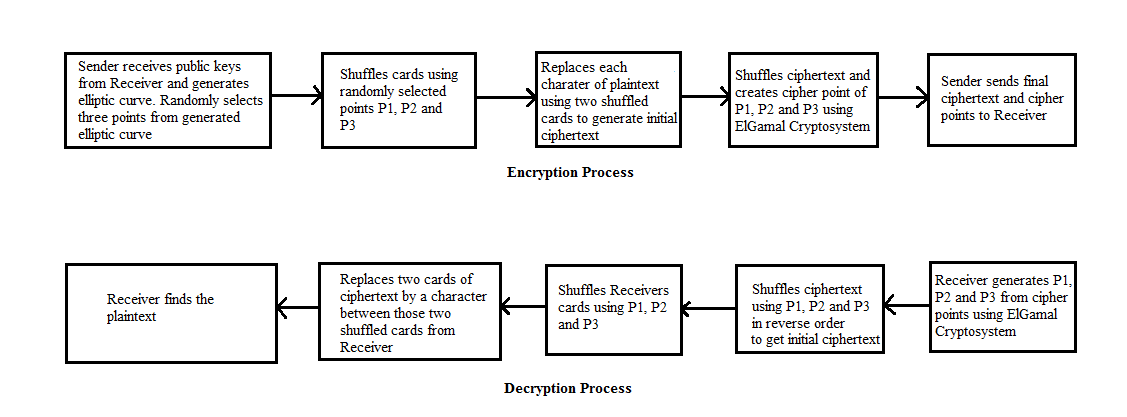 | Figure (1a). Proposed Mechanism |
3.1. Key Generation for Text Encryption and Decryption
The key generation is same as ElGamal Cryptosystem using Elliptic Curve. Receiver chooses Ep(a,b) with an elliptic curve over GF(p), e1 is a point on elliptic curve, e1=(x1, y1). e2=d×e1, where d is the private key. Receiver announces public keys Ep(a,b), e1 and e2.
3.2. Encryption Process
Sender receives public keys Ep(a,b), e1 and e2 from receiver. Sender chooses three points over elliptic curve P1, P2 and P3. Sender uses those points to shuffle 52 cards. 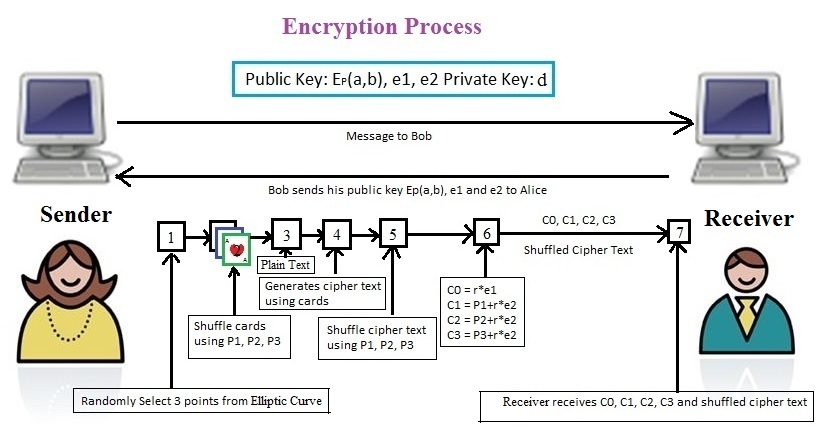 | Figure (1b). Encryption process of proposed method |
3.2.1. Card Shuffling Process
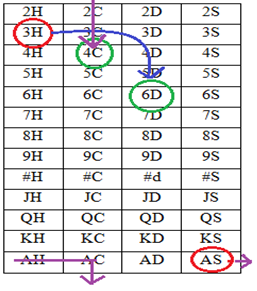
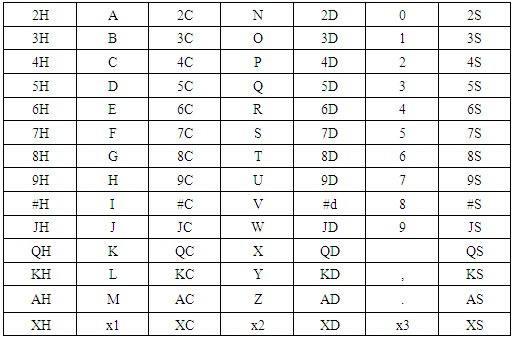
Consider 4×13 matrix for cards, Here 2H= 2 of Hearts, 3H= 3 of Hearts…… 9H=9 of Hearts, #H=10 of Hearts (10H has three characters but in our process need 2 character to present each card; so, we replace 10 by special character #) JH= Jack of Hearts, QH=Queen of Hearts, KH=King of Hearts and AH=Ace of Hearts.2C= 2 of Clubs, 3C= 3 of Clubs…… 9C=9 of Clubs, #C=10 of Clubs (10C has three characters but in our process need 2 character to present each card; so, we replace 10 by special character #) JC= Jack of Clubs, QC=Queen of Clubs, KC=King of Clubs and AC=Ace of Clubs.2D= 2 of Dice, 3D= 3 of Dice…… 9D=9 of Dice #D=10 of Dice (10D has three characters but in our process need 2 character to present each card; so, we replace 10 by special character #) JD= Jack of Dice, QD=Queen of Dice, KD=King of Dice and AD=Ace of Dice.2S= 2 of Spade, 3S= 3 of Spade…… 9S=9 of Spade #S=10 of Spade (10S has three characters but in our process need 2 character to present each card; so, we replace 10 by special character #) JS= Jack of Spade, QS=Queen of Spade, KS=King of Spade and AS=Ace of Spade.Position of Matrix (1) 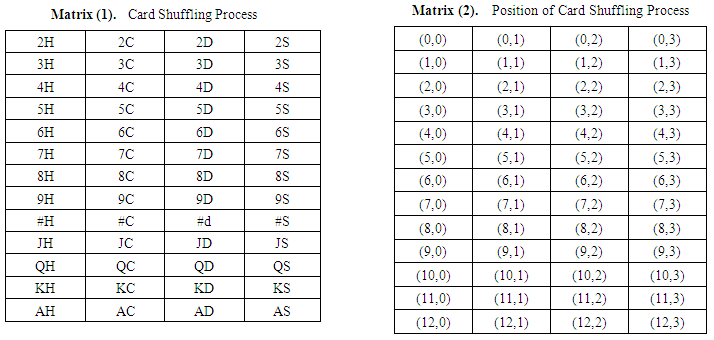 | Matrix (1)& (2) |
For point P1(x,y) : each card x steps right and y step downIf card current position is (i,j) in the matrix. We can find new position (i1,j1) by applying P1(x,y) for m×n matrix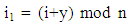 | (1) |
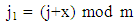 | (2) |
In this case matrix size is 4×13If P1(x,y) =(2,3) from Matrix(1) 3H current position is (1,0)So, x=2, y=3, i=1 and j=0. Now 3H new position is i1 = (1+3) mod 13 = 4 j1 = (0+2) mod 4 = 23H new position (4,2). That means 3H moves 2 steps right and 3 steps downFrom Matrix (1) AS position is (12,3)So, x=2, y=3, i=12 and j=3. Now AS new position is i1 = (12+3) mod 13 = 2 j1 = (3+2) mod 4 = 1AS new position (2,1). In this case when there is no scope to go right (at the last position of row) it will continue with current row first position. This is also similar with the column when there is no scope to go down (at the last position of column) it will continue with current column first position.Two operations P1(x,y) are shown below on Table (3).Table (3). Appling two operations of P1(x,y)
 |
| |
|
Applying P1 for all the cards we get. 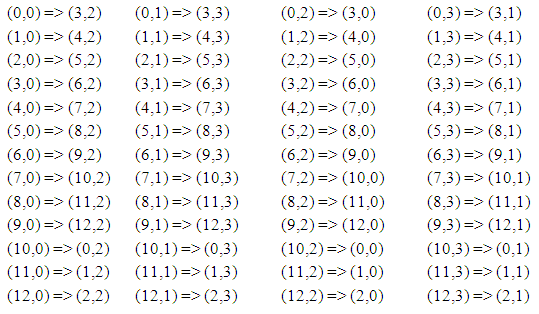 For point P2(x,y) : each card x steps left and y step upIf card current position is (i,j) in the matrix. We can find new position (i2,j2) by applying P2(x,y) for m×n matrix.
For point P2(x,y) : each card x steps left and y step upIf card current position is (i,j) in the matrix. We can find new position (i2,j2) by applying P2(x,y) for m×n matrix. | (3) |
 | (4) |
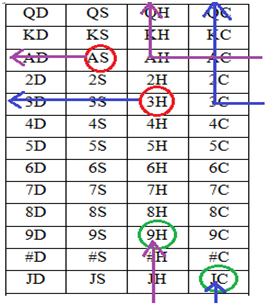
In this case matrix size 4×13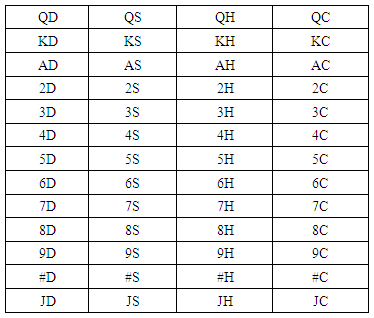 | Matrix (3). After Appling P1(x,y) operations |
If P2(x,y) =(3,5) from Matrix (3) after doing P1(x,y) operation, 3H current position is (4,2)So, x=3, y=5, i=4 and j=2. Now 3H 2nd new position is i2 = (4-5) mod 13 = 12 j2 = (2-3) mod 4 = 33H 2nd new position (12,3). That means 3H moves 3 steps left and 3 steps upIn this case when there is no scope to go left (at the first position of row) it will continue with current row last position. This is also similar with the column when there is no scope to go up (at the first position of column) it will continue with current column last position.After applying P1(x,y) operation from Matrix (3) AS current position is (2,1)So, x=3, y=5, i=2 and j=1. Now AS new position is i1 = (2-5) mod 13 = 10 j1 = (1-3) mod 4 = 2AS 2nd new position (10,2). Two operations of P2(x,y ) are shown below.Table (4). Two operations of P2(x,y)
 |
| |
|
Applying P2 for all the cards we get,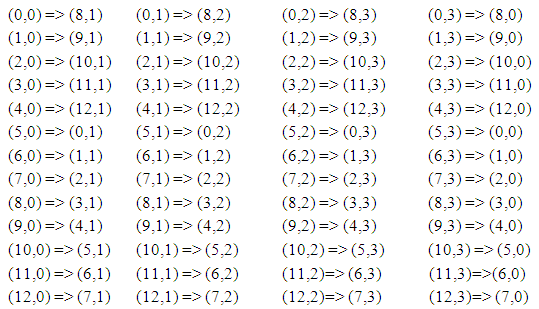 After changing all the position we get the matrix (4).
After changing all the position we get the matrix (4).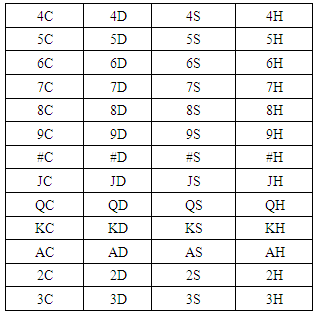 | Matrix (4). Position after operation of P2(x,y ) |
For P3(x,y) each card shift x steps, each card shift y steps shown by Table (5).x steps shift contains with those cards which are in the boundary of the matrix. And y steps shift with 2nd and 3rd column except first and last row of the matrix.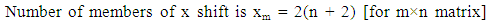 | (5) |
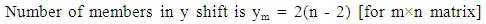 | (6) |
Number of member of x shift is 2(13+2) or 30 and number of member in y shift is 2(13-2) or 22.Now modifying our selected elliptic curve point is P3(x mod xm, y mod ym)Table (5). P3(x,y) card shifting
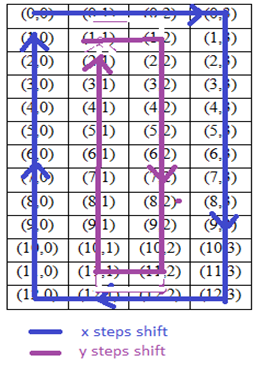 |
| |
|
Shifting x steps (Clockwise): Here we representing each card position by (i,j) and all the points which belongs to x shift are added to an array, size of the array is number of member for the x shifts and k is the array position. We have to determine new position kn for each card after x shifts.Suppose our randomly selected third point over elliptic curve is (2,1)Now, P3(2 mod 30, 1 mod 26) or P3(2,1)Now, x = 2Shifting 2 steps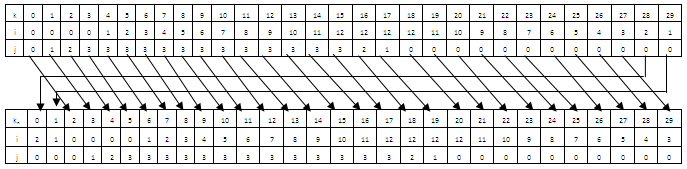 Now, move card k=29 to new position kn=1 move card k=28 to new position kn=0 ... … … … … … … … … move card k=0 to new position kn=2
Now, move card k=29 to new position kn=1 move card k=28 to new position kn=0 ... … … … … … … … … move card k=0 to new position kn=2 | (7) |
Shifting y steps (Clockwise): Here we representing each card position by (i,j) and all the points which belongs to y shift are added to an array, size of the array is number of member for the y shifts and k is the array position. We have to determine new position kn for each card after y shifts.Suppose randomly selected third point from elliptic curve is (2,1)Now, P3(2 mod 30, 1 mod 26) or P3(2,1)Now, y = 1Shifting 1 step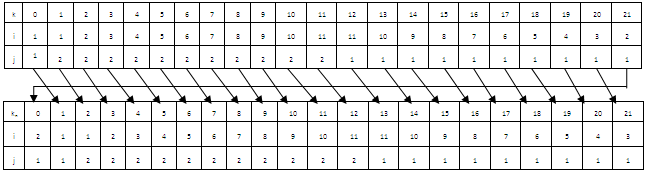 Now, move card k=0 to new position kn=1 move card k=1 to new position (0, 0) kn=2 ... … … ... … … ... … … move card k=21 to new position kn=0
Now, move card k=0 to new position kn=1 move card k=1 to new position (0, 0) kn=2 ... … … ... … … ... … … move card k=21 to new position kn=0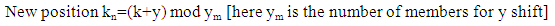 | (8) |
After shifting x=2 steps, we get in Matrix (5);After shifting y=1 steps, we get in Matrix (6);
3.3. Decryption Process
Receiver has public keys Ep(a,b), e1, e2 and private key d, and receives from sender final cipher text CCD9C75SC2CJD5D69CD8SJ63, C0, C1, C2 and C3. Receiver retrieves P1, P2 and P3 from C0, C1, C2 and C3 using following formula.P1=C1-d×C0 ; P2=C2-d×C0; P3=C3-d×C0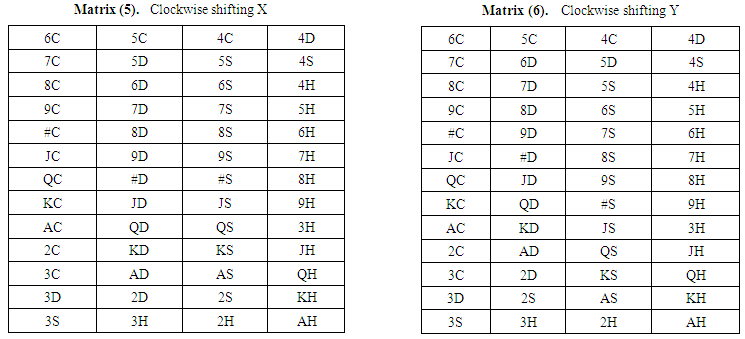 | Matrix (5)& (6) |
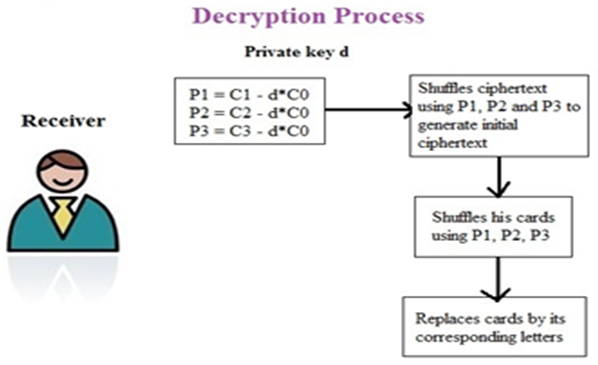 | Figure (1c). Decryption process of proposed method |
Now receiver arranges final cipher text by 4×(cipher_text_length/4) or 4×(24/4) or 4×6Position of Matrix (7) is shown on Matrix (8).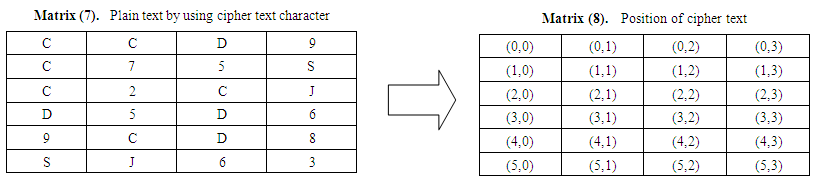 | Matrix (7)&(8) |
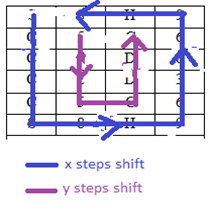
After then from P3(x,y) receiver shifts same way maintained before x steps and y steps but in anti-clockwise (shown below)Table (6). Shifting Anti-clockwise
 |
| |
|
x steps shift contains with those cards which are in the boundary of the matrix. And y steps shift with 2nd and 3rd column except first and last row of the matrix.Here matrix size 4×6. Number of members of x shift is 2(6+2) or 16 [from eqn 5] and number of members in y shift is 2(6 - 2) or 2×4 or 8 [from eqn 6] [Note that: Number of row is cipher_text_length/4 or 24/4 or 6]Now our modified elliptic curve point is P3(x mod xm, y mod ym)Shifting x steps (Anticlockwise): Here we representing each card position by (i,j) and all the points which belongs to x shift are added to an array, size of the array is number of member for the x shifts and k is the array position. We have to determine new position kn for each card after x shifts.Suppose we select our third point from elliptic curve is (2,1)Now, P3(2 mod 16, 1 mod 8) or P3(2,1)Now, x = 2Shifting 2 steps anticlockwise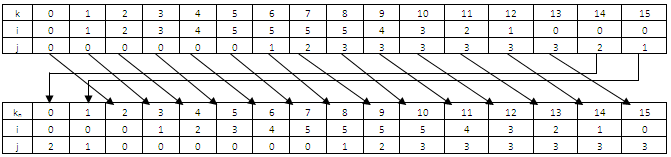 Now, move card k=0 to new position kn=14 move card k=1 to new position kn=15 ... … … … … … … … … move card k=15 to new position kn=13
Now, move card k=0 to new position kn=14 move card k=1 to new position kn=15 ... … … … … … … … … move card k=15 to new position kn=13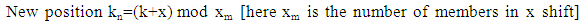 | (9) |
Shifting y steps (Anticlockwise): Here we representing each card position by (i,j) and all the points which belongs to y shift are added to an array, size of the array is number of member for the y shifts and k is the array position. We have to determine new position kn for each card after y shifts.Suppose randomly selected third point from elliptic curve is (2,1)Now, P3(2 mod 16, 1 mod 12) or P3(2,1)Now, y = 1, Shifting 1 step anticlockwise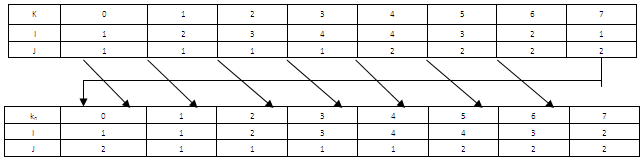 Now, move card k=7 to new position kn=6 move card k=6 to new position (0, 0) kn=6 ... … … … … … … … … move card k=0 to new position kn=7
Now, move card k=7 to new position kn=6 move card k=6 to new position (0, 0) kn=6 ... … … … … … … … … move card k=0 to new position kn=7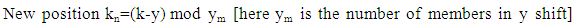 | (10) |
After shifting x=2 steps anti-clockwise in Matrix (9);After shifting y=1 steps anticlockwise in Matrix (10):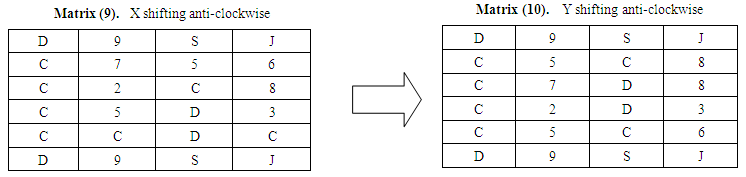 | Matrix (9)& (10) |
Now for P2(x,y) shifting x steps right and y steps downwards.[reverse of encryption process]After shifting P2(3,5) in Matrix (11);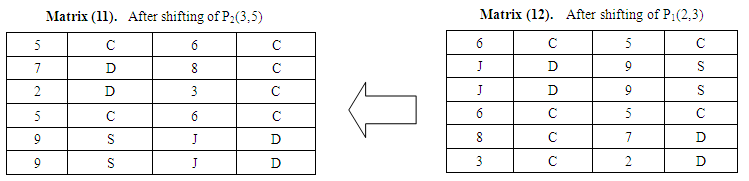 | Matrix (11)& (12) |
Now for P1(x,y) shifting x steps left and y steps upwards.[reverse of encryption process]After shifting P1(2,3) in Matrix (12). Now arrange this matrix row by row for new cipher text: 6C5CJD9SJD9S6C5C8C7D3C2D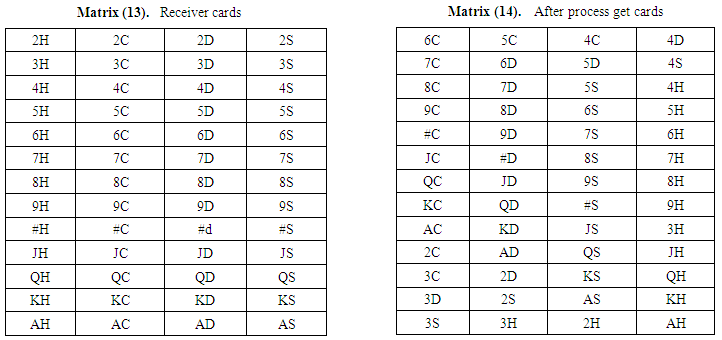 | Matrix (13)& (14) |
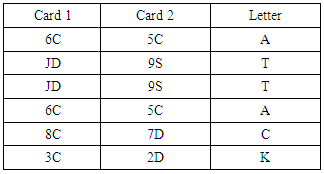
Now to find out which text inside of each two cards lets shuffle receiver card using P1, P2 and P3 on Matrix (13). The process is same as encryption process. After doing all the process we get shuffled cards shown by on Matrix (14).Now place each character between two cards, the table is given below on Matrix (15).Now replace each pairs of cards (from new cipher text) by letter between them.New cipher text = 6C5CJD9SJD9S6C5C8C7D3C2D on Table (7).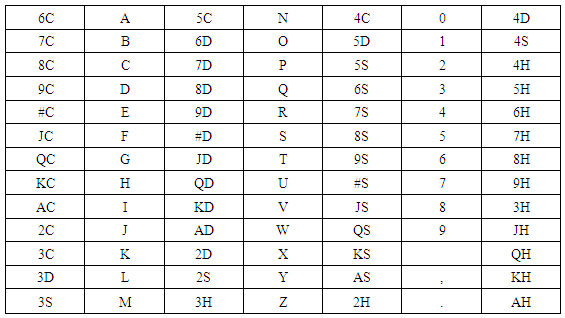 | Matrix (15). Character between two cards |
Table (7). Pairs of Cards
 |
| |
|
Now receiver gets plain text “ATTACK”End of decryption process shown on Table (8).Table (8). End of decryption process
 |
| |
|
Introducing New CharactersHere new cards XH, XC, XD and XS can be introduced for new characters x1, x2 and x3. The existing formula is same as before, no need to change the formula to introduce new characters. If we don’t need any character we can leave it as “null” or white space. Finally, as our proposed algorithm selects three random points for every message it provides differently shuffled cards in every single message. Thus we can say our mapping is dynamic.
4. Summary
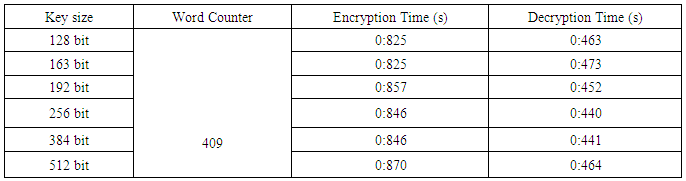
Encryption:Step 1: Sender receives public key EP(a,b), e1 and e2 from receiver.Step 2: Sender creates an elliptic curve using EP(a,b) and randomly selects three points (P1, P2 and P3) over elliptic curve.Step 3: Sender shuffles his playing cards (4×13 matrix) using P1, P2 and P3. Step 4: Sender puts each character between two cards which is shuffled in step 3.Step 5: Sender replaces each character by two cards from its left and right, and creates initial ciphertext.Step 6: Sender shuffles his initial ciphertext using P1, P2 and P3 and creates final ciphertextStep 7: Sender encrypts randomly selected point P1, P2 and P3 using idea of ElGamal Cryptosystem and gets C0, C1, C2 and C3.Step 8: Sender sends C0, C1, C2 and C3 and final ciphertext to the receiverDecryption:Step 1: Receiver decrypts C0, C1, C2 and C3 and gets P1, P2 and P3 using his private key d.Step 2: Receiver reversely shuffles final ciphertext using P1, P2 and P3 and gets initial ciphertext.Step 3: Receiver shuffles his playing cards using P1, P2 and P3, Step 4: Receiver puts each character between two cards which is shuffled in step 3.Step 5: Receiver replaces each two cards of initial ciphertext by character between them. Step 6: Completing replacement of all the cards from initial ciphertext receiver gets plaintext.Simulation Result Simulation is done by using Toshiba Satellite C600 with system configuration dual core processor @2.30 GHz and 2 GB Ram. Word length= 409, Text Length: 2325Table (2a). Simulation result for encryption and decryption time
 |
| |
|
 | Figure (2a). Simulation Graph for Time (Encryption) |
 | Figure (2b). Simulation Graph for Time (Decryption) |
From table (2a), figure (2a) and (2b) we can see that bit size does not affect our algorithms encryption and decryption time. Comparison As our proposed of algorithm requires mapping, we compared our algorithm with those algorithm which requires mapping. Implementation of Elliptic Curve Cryptography on Text and Image [7] and Implementation of Text based Cryptosystem using Elliptic Curve Cryptography [6] simulation was performed using Lenovo ideapad Z510 laptop with system configuration of i7 processor @2.20GHz and 8GB Ram [6]. Our simulation is done by using Toshiba Satellite C600 with system configuration dual core processor @2.30 GHz and 2 GB Ram. Word length=409, Text Length: 2325. We have done our comparison with only those methods where mapping is required. Table (3a). Simulation result of referenced method
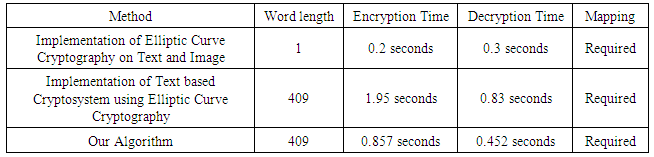 |
| |
|
Though our simulation environment is better than referenced environment, our algorithm performs better then referenced methods.Simulation Result of Image Encryption/DecryptionThe implementation is performed on i7 CPU 2.20GHz lenovo laptop with 8 GB RAM using Mathematica version 10. The Elliptic curve used here is the 512 bit Standard Elliptic curve given by Elliptic Curve Cryptography.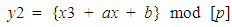 | (11) |
where  The sender sends the cipher image along with the Digital Signature calculated with the pixels value of the cipher image. The public key of the receiver was used to encrypt the image and the private key of the sender was used to provide digital signature to the cipher image being sent.While decrypting the cipher image, the receiver uses his private key to decrypt the cipher image. Authenticity provides the proof that the message came for the intended sender and integrity validates that the message was not altered or changed during the transit. An altered cipher image will generate.
The sender sends the cipher image along with the Digital Signature calculated with the pixels value of the cipher image. The public key of the receiver was used to encrypt the image and the private key of the sender was used to provide digital signature to the cipher image being sent.While decrypting the cipher image, the receiver uses his private key to decrypt the cipher image. Authenticity provides the proof that the message came for the intended sender and integrity validates that the message was not altered or changed during the transit. An altered cipher image will generate.
5. Conclusions
Data confidentiality is important to protect data from unauthorized access of confidential information. In this research work we have implemented a new way for text encryption and decryption using card shuffling logic which provides data confidentiality. For higher security with lesser key size, we use Elliptic curve in our research work.In our research work we have created initial cipher text by shuffling and mapping with playing cards. These cards are shuffled using three randomly selected points over elliptic curve. We have implemented double encryption process by shuffling the initial ciphertext using those randomly selected points and generate final ciphertext for more security. From the performance table, comparison table and security analysis section we can observe that our proposed algorithm has a lot of positive aspect. As Elliptic Curve Cryptography provides equal security like other cryptographic system but with less key size, it is very suitable for devices which have power, storage and processing limitation. So, our algorithm can be implemented in that device where less processing power and energy requires.
References
| [1] | William Stallings, ―Cryptography and Network Security, Principles and Practice‖, [Forth Edition], Pearson Education Inc., 2006. |
| [2] | Behrouza A. Forouzan and Debdeep Mukhopadhyay, ―Cryptography and Network Security‖, [Second Edition], McGraw Hill Education Private Limited, 2008. |
| [3] | Georgios Loukas and Gulay Oke, ―Protection against Denial of Service Attacks: A Survey‖, Oxford University Press, 2009. |
| [4] | Laiphrakpam Dolendro Singh and Khumanthem Manglem Singh, Implementation of Text Encryption using Elliptic Curve Cryptography, ELSEVIER, ScienceDirect, Procedia Computer Science 54(2015) 73-82 (2015). |
| [5] | D. Sravana Kumar, CH. Suneetha and A. ChandrasekhAR, Encryption of Data using Elliptic Curve over Finite Fields, IJDPS Vol.3, No.1, January 2012. |
| [6] | S. Maria Celestin Vigila and K. Munesswaran, Implementation of Text based Cryptosystem using Elliptic Curve Cryptography, International Conference on Advance Computing, IEEE, pp. 82-85, December (2009). |
| [7] | Megha Kolhekar Anita Jadhav Implementation of Elliptic Curve Cryptography on Text and Image, International Journal of Enterprise Computing and Business System, vol. 1, issue 2, July (2011). |





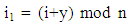
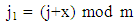
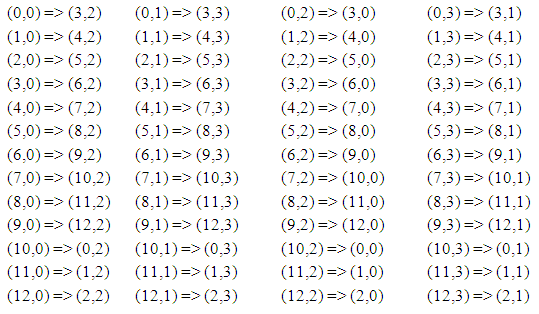 For point P2(x,y) : each card x steps left and y step upIf card current position is (i,j) in the matrix. We can find new position (i2,j2) by applying P2(x,y) for m×n matrix.
For point P2(x,y) : each card x steps left and y step upIf card current position is (i,j) in the matrix. We can find new position (i2,j2) by applying P2(x,y) for m×n matrix.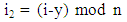
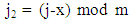

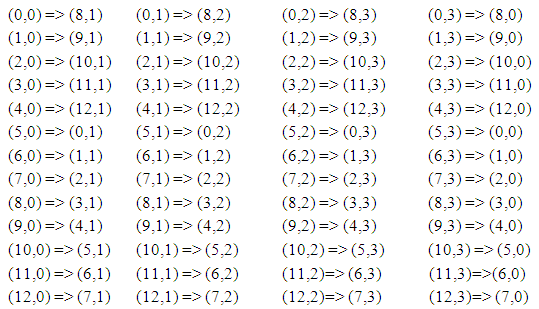 After changing all the position we get the matrix (4).
After changing all the position we get the matrix (4).
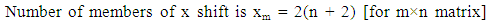
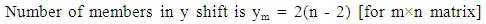
 Now, move card k=29 to new position kn=1 move card k=28 to new position kn=0 ... … … … … … … … … move card k=0 to new position kn=2
Now, move card k=29 to new position kn=1 move card k=28 to new position kn=0 ... … … … … … … … … move card k=0 to new position kn=2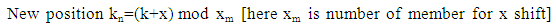
 Now, move card k=0 to new position kn=1 move card k=1 to new position (0, 0) kn=2 ... … … ... … … ... … … move card k=21 to new position kn=0
Now, move card k=0 to new position kn=1 move card k=1 to new position (0, 0) kn=2 ... … … ... … … ... … … move card k=21 to new position kn=0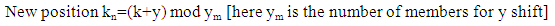



 Now, move card k=0 to new position kn=14 move card k=1 to new position kn=15 ... … … … … … … … … move card k=15 to new position kn=13
Now, move card k=0 to new position kn=14 move card k=1 to new position kn=15 ... … … … … … … … … move card k=15 to new position kn=13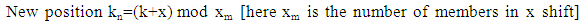
 Now, move card k=7 to new position kn=6 move card k=6 to new position (0, 0) kn=6 ... … … … … … … … … move card k=0 to new position kn=7
Now, move card k=7 to new position kn=6 move card k=6 to new position (0, 0) kn=6 ... … … … … … … … … move card k=0 to new position kn=7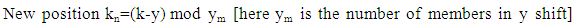






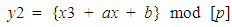
 The sender sends the cipher image along with the Digital Signature calculated with the pixels value of the cipher image. The public key of the receiver was used to encrypt the image and the private key of the sender was used to provide digital signature to the cipher image being sent.While decrypting the cipher image, the receiver uses his private key to decrypt the cipher image. Authenticity provides the proof that the message came for the intended sender and integrity validates that the message was not altered or changed during the transit. An altered cipher image will generate.
The sender sends the cipher image along with the Digital Signature calculated with the pixels value of the cipher image. The public key of the receiver was used to encrypt the image and the private key of the sender was used to provide digital signature to the cipher image being sent.While decrypting the cipher image, the receiver uses his private key to decrypt the cipher image. Authenticity provides the proof that the message came for the intended sender and integrity validates that the message was not altered or changed during the transit. An altered cipher image will generate. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML








