Md Obaidur Rahaman
Department of Computer Science and Engineering, European University of Bangladesh, Bangladesh
Correspondence to: Md Obaidur Rahaman, Department of Computer Science and Engineering, European University of Bangladesh, Bangladesh.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Data Security has become very important in today’s world, as a result of which various methods are adopted to bypass it. With the advent of the internet, security became a major concern and the history of security allows a better understanding of the emergence of security technology. The internet structure itself allowed for many security threats to occur. The mechanism of the internet, when modified can reduce the possible attacks that can be sent across the network. Knowing the attack methods, allows for the appropriate security to emerge. Many modern spare secure themselves from the internet by means of decryption and encryption mechanisms. This paper outlines the various attack methods which are used, as well as various mechanism against them.
Keywords:
Data and Information Security
Cite this paper: Md Obaidur Rahaman, Data and Information Security in Modern World, Computer Science and Engineering, Vol. 7 No. 1, 2017, pp. 12-21. doi: 10.5923/j.computer.20170701.02.
1. Introduction
Data security is one of the most important issues in the modern civilization. In this modern world most of the data are transferred and stored using internet. So it is important to secure our data from unauthorized access. Computer scientists are developing different types of mechanism to secure data. As old mechanisms are destroyed by different types of unauthorized attacks, computer scientists are developing new and modern types of security mechanism to protect data. Data are encrypted thus unauthorized user can’t get actual data and decrypted to use by authorized user. Cryptology is the study of secure communications, which encompasses both cryptography and cryptanalysis [1]. Encrypted data must be decrypted to authorize user to make that data useable. Encryption is the conversion of plaintext or data into unintelligible form by means of a reversible translation, based on a translation table or algorithm, this is also called enciphering [1]. On the other hand decryption is the translation of encrypted text or data (called ciphertext) into original text or data (called plaintext), this is also called deciphering [1]. A strong data encryption and decryption technique is required to provide confidentiality of sensitive data from security attacks.
2. Security Goals and Threats
Security GoalsAll information security measures try to address at least one of three goals:Ÿ Protect the confidentiality of dataŸ Preserve the integrity of dataŸ Promote the availability of data for authorized useThese goals form confidentiality, integrity, availability (CIA) triad, the basis of all security programs. Information security professionals who create policies and procedures must consider each goal when creating a plan to protect a computer system [2].
2.1. Confidentiality
Confidentiality is the concealment of information or resources. The need for keeping information secret arises from the use of computers in sensitive fields such as government and industry. For example, military and civilian institutions in the government often restrict access to information to those who need that information. Valuable information or sensitive data must be protected from unathorized access. Access control mechanisms support confidentiality. A cryptographic key controls access to the unscrambled data, but then the cryptographic key itself becomes another datum to be protected.
2.2. Integrity
Integrity refers to the trustworthiness of data or resources, and it is usually phrased in terms of preventing improper or unauthorized change. Integrity includes data integrity, (the content of the information) and origin integrity (the source of the data, often called authentication). The source of the information may bear on its accuracy and credibility and on the trust that people place in the information. Integrity mechanisms fall into two classes: prevention mechanisms and detection mechanisms. Prevention mechanisms seek to maintain the integrity of the data by blocking any unauthorized attempts to change the data or any attempts to change the data in unauthorized ways. The distinction between these two types of attempts is important. Detection mechanisms do not try to prevent violations of integrity; they simply report that the data’s integrity is no longer trustworthy.
2.3. Availability
Availability refers to the ability to use the information or resource desired. Availability is an important aspect of reliability as well as of system design because an unavailable system is at least as bad as no system at all. The aspect of availability that is relevant to security is that someone may deliberately arrange to deny access to data or to a service by making it unavailable. System designs usually assume a statistical model to analyze expected patterns of use, and mechanisms ensure availability when that statistical model holds. Someone may be able to manipulate use (or parameters that control use, such as network traffic) so that the assumptions of the statistical model are no longer valid. This means that the mechanisms for keeping the resource or data available are working in an environment for which they were not designed. As a result, they will often fail.
3. Threats to Security Goals
A threat is a potential violation of security. The violation need not actually occur for there to be a threat. The fact that the violation might occurs means that those actions that could cause it to occur must be guarded against (or prepared for). Those actions are called attacks. Those who execute such actions, or cause them to be executed, are called attackers. Our three goals of security – confidentiality, integrity, and availability – can be threatened by security attacks. The threats are divided into three groups related to the security goals [1].
3.1. Threats to Confidentiality
In data confidentiality two types of attack can be mention as threat. They are snooping and traffic analysis. Unauthorized access or interception of a confidential data is known as snooping. Snooping the unauthorized interception of information, is a form of disclosure. It is passive, suggesting simply that some entity is listening to (or reading) communications or browsing through files or system information. For example, a file transferred through the Internet may contain confidential information.
3.2. Threats to Integrity
The integrity of data can also be threatened by several kinds of attack such as: modification, masquerading, replaying and repudiation. After intercepting or accessing information data can be modified by unauthorized access. Modification means some portion of legitimate data is altered or delayed or reordered. The attacker intercepts the message and changes the types of transaction to benefit her. Unlike snooping, modification is active; it results from entity changing information. Active wiretapping is a form of modification in which data moving across a network is altered; the term active distinguishes it from snooping (passive wiretapping).
3.3. Threats to Availability
In security goal, there is only one attack threatening availability is called denial of service (DoS). Denial of service, a long-term inhibition of service, is a form of usurpation, although it is often used with other mechanisms to deceive. The attacker prevents a server from providing a service. The denial may occur at the source (by preventing the server from obtaining the resources needed to perform its function), at the destination (by blocking the communications from the server), or along the intermediate path (by discarding messages from either the client or the server, or both). Denial of service poses the same threat as an infinite delay [3]. Availability mechanisms counter this threat. Denial of service or delay may result from direct attacks or from non security related problems.
4. Cryptography
Cryptography is closely related to the disciplines of cryptology and cryptanalysis. Cryptography includes techniques such as microdots, merging words with images, and other ways to hide information in storage or transit. However, in today's computer-centric world, cryptography is most often associated with scrambling plaintext (ordinary text, sometimes referred to as cleartext) into ciphertext (a process called encryption), then back again (known as decryption). Individuals who practice this field are known as cryptographers. The basic component of cryptography is a cryptosystem.
4.1. Types of Cryptographic Algorithms
There are several ways of classifying cryptographic algorithms. For purposes of this paper, they will be categorized based on the number of keys that are employed for encryption and decryption, and further defined by their application and use. The two types of algorithms that will be discussed are (Figure 3.1): Ÿ Secret Key Cryptography (SKC): Uses a single key for both encryption and decryption. Ÿ Public Key Cryptography (PKC): Uses one key for encryption and another for decryption.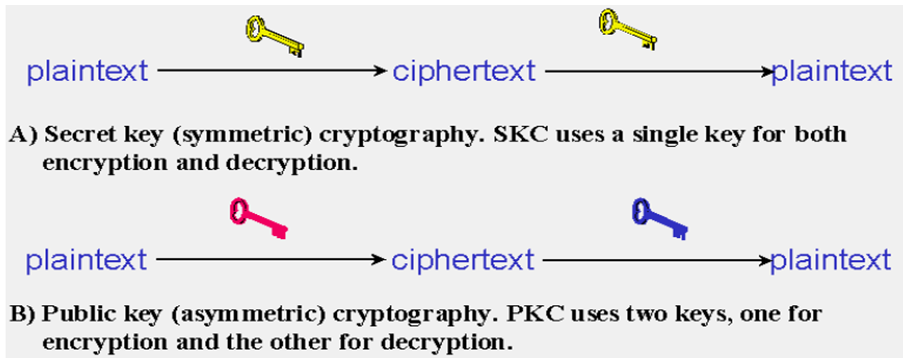 | Figure 3.1. The two types of algorithms SKC & PKC |
4.2. Secret Key Cryptography
With secret key cryptography, a single key is used for both encryption and decryption. As shown in Figure 3.1A, the sender uses the key (or some set of rules) to encrypt the plaintext and sends the ciphertext to the receiver. The receiver applies the same key (or ruleset) to decrypt the message and recover the plaintext. Because a single key is used for both functions, secret key cryptography is also called symmetric encryption.There are two basic types of symmetric key/secret key ciphers: Ÿ Transposition ciphersŸ Substitution ciphersTransposition CiphersIn cryptography, a transposition cipher is a method of encryption by which the positions held by units of plaintext (which are commonly characters or groups of characters) are shifted according to a regular system, so that the ciphertext constitutes a permutation of the plaintext. That is, the order of the units is changed (the plaintext is reordered). A transposition cipher rearranges the characters in the plaintext to form the ciphertext. The letters are not changed. Substitution ciphersA substitution cipher changes characters in the plaintext to produce the ciphertext. It is a method of encoding by which units of plaintext are replaced with ciphertext, according to a fixed system; the "units" may be single letters (the most common), pairs of letters, triplets of letters, mixtures of the above, and so forth. The receiver decrypts the text by performing the inverse substitution. There are a number of different types of substitution cipher. If the cipher operates on single letters, it is termed a simple substitution cipher; a cipher that operates on larger groups of letters is termed polygraphic.
4.3. Public-Key Cryptography
Public-key cryptography is any system of encryption that uses a pair of cryptographic keys, where the system has the property that simply possessing one does not allow the practical calculation of the other. Typically the public key is used for encryption and may be disseminated widely, while the other - the private key, is used for decryption and is known only to the owner. Using the public key, any person can encrypt a message for the owner, and such message can only be decrypted with the owner's private key. Thus a message intended for a specific recipient can be encrypted and hosted safely on public servers with only the private key owner being able to read it. This system of using two different paired keys is called an asymmetric key encryption algorithm. The symmetric encryption/decryption is based on simpler algorithms and is much faster. [1] Public-key cryptography algorithms that are in use today for key exchange or digital signatures include.
4.4. Elliptic Curve Cryptography (ECC)
An elliptic curve is simply the locus of points in the x-y plane that satisfy an algebraic equation 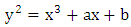 of the form. Each choice of numbers a and b yields different elliptic curves. The value of x, y, a and b may be from any field, namely complex number, real number, finite number and so on [5].
of the form. Each choice of numbers a and b yields different elliptic curves. The value of x, y, a and b may be from any field, namely complex number, real number, finite number and so on [5].
4.5. ElGamal Cryptosystem using Elliptic Curve [2]
Several methods have been used to encrypt and decrypt using elliptic curves. The common one is to simulate the ElGamal cryptosystem using an elliptic curve over GF(p) or 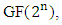 as shown in the following figure 3(a).Here Ep(a,b), e1 and e2 are public key and d is the private key of the receiver.
as shown in the following figure 3(a).Here Ep(a,b), e1 and e2 are public key and d is the private key of the receiver.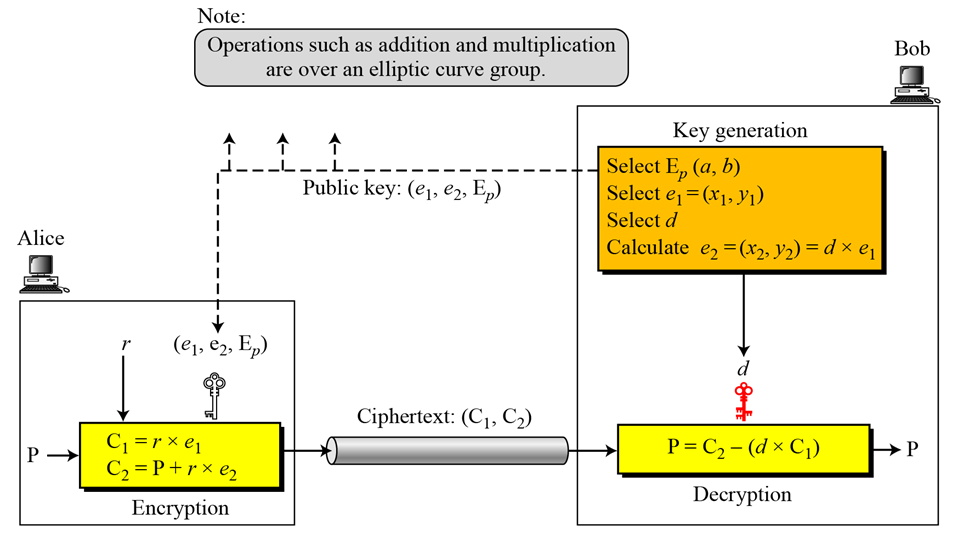 | Figure (3a). ElGamal Cryptosystem using the Elliptic Curve |
5. Elliptic Curve Cryptography
5.1. Finding Points on the Curve
Algorithm in the following shows the pseudocode for finding the points on the curve 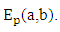 Algorithm
Algorithm 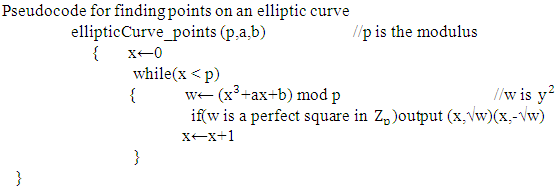 Example: Consider y2 = x3 + 2x + 3 (mod 5)
Example: Consider y2 = x3 + 2x + 3 (mod 5)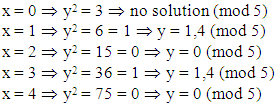 Then points on the elliptic curve are , (1,1) (1,4) (2,0) (3,1) (3,4) (4,0) and the point at infinity:
Then points on the elliptic curve are , (1,1) (1,4) (2,0) (3,1) (3,4) (4,0) and the point at infinity: 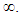
5.2. Addition of Two Points
Let the points P = (x1, y1) and Q= (x2, y2) be in the elliptic group Ep (a, b), and O is the point at infinity. The rules for addition over the elliptic group Ep (a, b) are:1. P+O=O+P=P2. If x2= x1 and y2 = -y1, that is P = (x1, y1) and Q= (x2, y2) = (x1, -y1) = −P, then P+Q=O.3. If Q ≠ −P, then the sum P+Q = (x3, y3) is given by:x3 = λ2 - x1- x2 mod py3 = λ( x1- x3) - y1 mod pWhere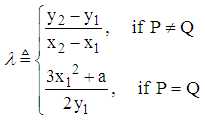
5.3. Subtraction of Two Points
Let the points P = (x1, y1) and Q = (x2, y2) be in the elliptic group Ep (a, b). The rules for subtraction over the elliptic group Ep (a, b) are:1. P−Q=P+(−Q)=P+(inverse of Q), so the inverse of Q is Q(x2, y2)= Q(x2, -y2)= Q(x2, p-y2).
5.4. Multiplication Points by a Constant
Let the points P = (x1, y1) and the integer be k in the elliptic group Ep (a, b). Then Pk= Add P with k times.e.g., 2P = P+P = (x1, y1) + (x1, y1) = (x3, y3).where 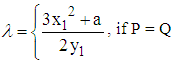 and x3 = λ2 - x1 - x2 mod p, y3 = λ (x1 - x3) - y1 mod p.
and x3 = λ2 - x1 - x2 mod p, y3 = λ (x1 - x3) - y1 mod p.
5.5. Finding an Inverse
Let the points P = (x1, y1) and Q = (x2, y2) be in the elliptic group Ep(a, b). Then the inverse of Q(x2, y2) can be calculated as Q(x2, n - y2) in Zn where n - y2 is called additive inverse in Zn.
5.6. Point generation on Elliptic Curve
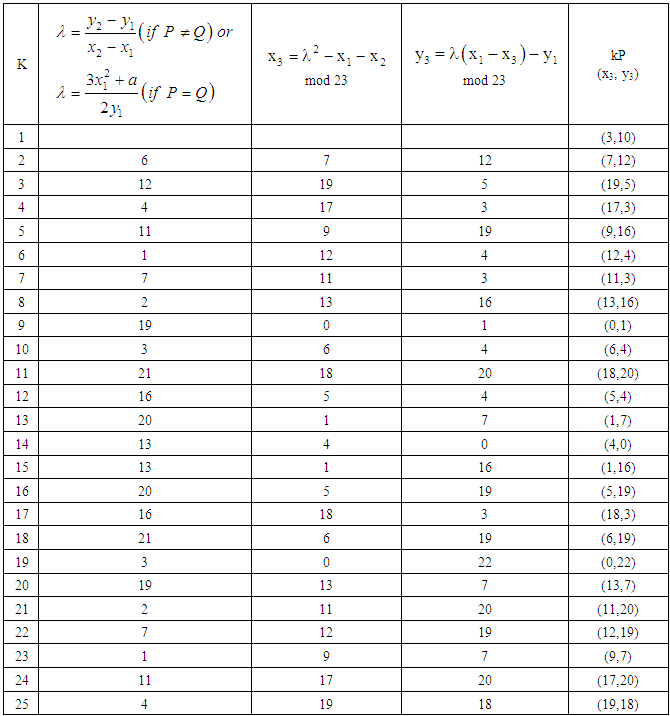
Let P = (3,10) ∈E23(1,1). Then 2P = (x3, y3) is equal to: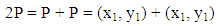 Since P=Q and x2 = x1, the values of λ, x3 and y3 are given by:
Since P=Q and x2 = x1, the values of λ, x3 and y3 are given by: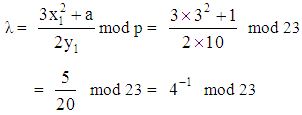 Considering,
Considering, 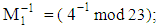 where,
where, 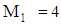 and m1 = 23Now using extended Euclidean formula:Here, quotient = q, remainder = r and t = t1 – qt2
and m1 = 23Now using extended Euclidean formula:Here, quotient = q, remainder = r and t = t1 – qt2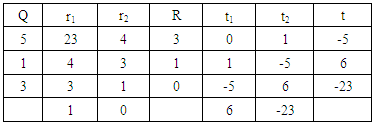 Since, r1 = 1So that,
Since, r1 = 1So that, 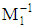 = t1 The extended Euclidean Algorithm gives t1 = 6. So, the multiplicative inverse
= t1 The extended Euclidean Algorithm gives t1 = 6. So, the multiplicative inverse 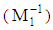 is 6 mod 23 =6.
is 6 mod 23 =6.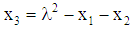 mod p = 62−3−3 mod 23 = 30 mod 23 = 7
mod p = 62−3−3 mod 23 = 30 mod 23 = 7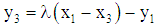 mod p = 6×(3−7)−10 mod 23 = −34 mod 23 = 12Therefore 2P = (x3, y3) = (7, 12).The multiplication kP is obtained by doing the elliptic curve addition operation k times by following the same additive rules.
mod p = 6×(3−7)−10 mod 23 = −34 mod 23 = 12Therefore 2P = (x3, y3) = (7, 12).The multiplication kP is obtained by doing the elliptic curve addition operation k times by following the same additive rules.Table (4a). Elliptic Curve point generation for E23(1,1)
 |
| |
|
6. Implementation of Text Encryption Using Elliptic Curve Cryptography
“Implementation of Text Encryption using Elliptic Curve Cryptography” [6] which avoids the costly operation of mapping and the need to share common lookup table between the sender and the receiver. They design the algorithm such a way that can be used to encrypt and decrypt any types of script with defined ASCII values. They discuss security issues and simulation of their algorithm.The communicating parties agrees upon an Elliptic curve equation 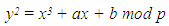 | (1.1) |
with the generator ‘G’ and makes the public keys ‘ P a’ and ‘ P b’ known to all and private keys ‘n A’ and ‘n B’ are kept secret. Here, they do not map the ASCII values of the characters to affine points of the elliptic curve. They group the ASCII values of the characters and perform cryptographic operation on the group. The size of each group is given by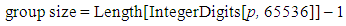 | (1.2) |
IntegerDigit [n, b] function in Mathematica gives a list of the base b digits in the integer n. Here, they choose base as 65536 because ASCII value is defined till 65535. Length is used to count the number of elements in the given expression. The group size help us to find the maximum number of characters that can be grouped up. Each group is converted into big integer values. They pair up the big integer value and use it as ‘Pm’ in the ECC operation. Pairing reduces the operation of mapping to elliptic coordinates and the need to share a common look up table. The whole encryption and decryption is shown as a block diagram in Fig. (5a).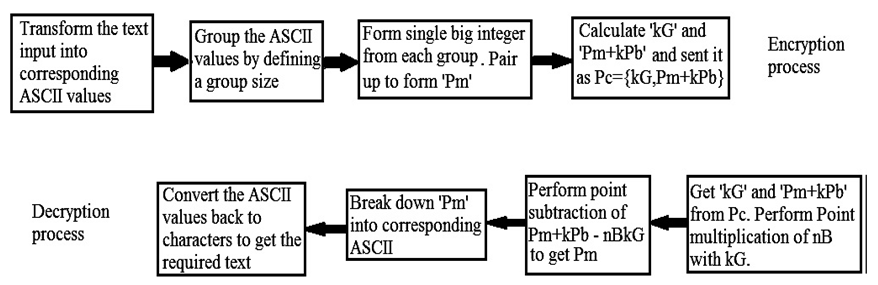 | Figure (5a). Encryption and Decryption process |
6.1. Encryption
Ÿ Obtain the text to be send.Ÿ Convert to its corresponding ASCII values.Ÿ Partition the ASCII value as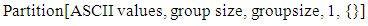 | (1.3) |
This operation group the ASCII values with size given by group size with no overlapping and the later sub lists that have size lesser than group size are left as it is without padding.Ÿ Each group obtained from the above step is converted into big integer values taking base as 65536.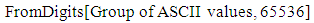 | (1.4) |
• Pad with 32 to the end of the list from the above step if the count of the above list is odd, to make it even for performing complete pairing. Each single pair will be an input to the ECC system as ‘P m’. We pad with 32 because 32 represent blank space in ASCII code.• Select random k value, k = Random value with range 1 to n − 1. Compute k G and k Pb using Point multiplication operation.• Compute P m + k P b using point addition or point doubling as required.• Send P c = {k G, P m + k P b} as cipher text to the receiver side.
6.2. Decryption
• Get the cipher text P c.• Get the left part k G and right part P m + k P b of the P c separately.• Multiply with n B to the left part and subtract it from the right part to get P m.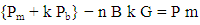 | (1.5) |
Since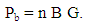 | (1.6) |
Subtraction operation can be converted to addition by multiplying with −1 to the y coordinate. This operation can be justified with point addition operation. In point addition we used to get the mirror image point over the x -axis. Example:- {97, 24} = {97, −24}.• The above operation will yield the big integer value which is formed by combining group of ASCII values. Convert it back to list of ASCII values.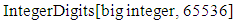 | (1.7) |
IntegerDigits [n, b] in Mathematica provides a list of the base b digits in the integer n. IntegerDigits and FromDigits function are inverse of each other, so the ASCII values are preserved during encryption and decryption.• Convert the list of ASCII values to its corresponding characters
6.3. Encryption of Data using Elliptic Curve over Finite Fields
“Encryption of Data using Elliptic Curve over Finite Fields” [7] which describes a new algorithm of text encryption and decryption using a mapping table which is created using elliptic curve.If two communicating parties Alice and Bob want to communicate the messages then they agree upon to use an elliptic curve Ep(a,b) where p is a prime number and a random point C on the elliptic curve. Alice selects a large random number α which is less than the order of Ep(a,b) and a point A on the elliptic curve. She computes A1 = α (C +A) and A2 = α A. She keeps the random number α and the point A as her private keys and publishes A1 and A2 as her general public keys. Similarly Bob selects a large random number β and a point B on the elliptic curve. He computesB1 = β (C+B) and B2 = β B. He keeps the random number β and the point B as his private keys and publishes B1 and B2 as his general public keys. After publishing the public keys, the communicating parties again calculate the following quantities and publish them as their specific public keys of each other.Alice calculates AB = α B2 and publishes it as her specific public key for Bob. Bob calculates BA = β A2 and publishes it as his specific public key for AliceAlice’s private key 1 = α, a large random number less than the order of the generatorAlice’s private key 2 = a point A on the elliptic curve Ep(a,b)Alice’s general public key 1 = a point A 1on the elliptic curve Ep(a,b)Alice’s general public key 2 = a point A 2 on the elliptic curve Ep(a,b)Alice’s specific public key for Bob = a point A B on the elliptic curve Ep(a,b)Bob’s private key 1 = β, a large random number less than the order of the generatorBob’s private key 2 = B, a point on the elliptic curve Ep(a,b)Bob’s general public key 1 = B 1, a point on the elliptic curve Ep(a,b)Bob’s general public key 2 = B 2, a point on the elliptic curve Ep(a,b)Bob’s specific public key for Alice = B A, a point on the elliptic curve Ep(a,b).
6.3.1. Encryption
If Bob wants to communicate the message M then all the characters of the message are coded to the points on the elliptic curve using the code table which is agreed upon by the communicating parties Alice and Bob. Then each message point is encrypted to a pair of cipher points E1, E2. He uses a random number γ which is different for the encryption of different message points.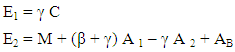 After encrypting all the characters of the message Bob converts the pair of points of each message point into the text characters using the code table. Then he communicates the cipher text to Alice in public channel.
After encrypting all the characters of the message Bob converts the pair of points of each message point into the text characters using the code table. Then he communicates the cipher text to Alice in public channel.
6.3.2. Decryption
After receiving the cipher text, Alice converts the cipher text into the points on the elliptic curve and recognizes the points E1 and E2 of each character. Then she decrypts the message as follows.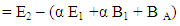 Decryption works out properly:-
Decryption works out properly:-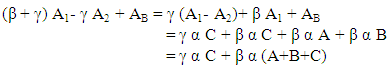
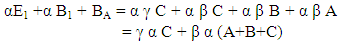
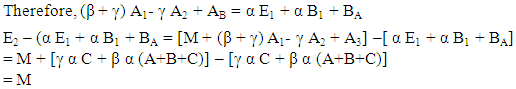 In this method a group of communicating parties A, B, C, D……. can communicate with one another securely, non- repudiatively in an authentic manner. Here each communicating party say X publishes two general public keys X1, X2. X also publishes a specific public key XY to be used by the communicating party Y for communication with Y. When Y wants to communicate with X, Y uses the general public keys of X (X1, X2), the specific public key published by X for Y (XY) and Y’s secret key y. To decrypt the message X uses Y’s general public keys (Y1, Y2), the specific public key published by Y for X (YX) and X’s secret key x. Here X creates specific public key XY for Y using Y’s public keys and X’s secret key. So, this method of encryption using elliptic curves over finite fields is highly suitable for communication between groups of corporate/government institutions.Example Consider an elliptic curve whose equation is y2 = x3 + 2x + 9. The graph of the function is shown in fig. (5b).
In this method a group of communicating parties A, B, C, D……. can communicate with one another securely, non- repudiatively in an authentic manner. Here each communicating party say X publishes two general public keys X1, X2. X also publishes a specific public key XY to be used by the communicating party Y for communication with Y. When Y wants to communicate with X, Y uses the general public keys of X (X1, X2), the specific public key published by X for Y (XY) and Y’s secret key y. To decrypt the message X uses Y’s general public keys (Y1, Y2), the specific public key published by Y for X (YX) and X’s secret key x. Here X creates specific public key XY for Y using Y’s public keys and X’s secret key. So, this method of encryption using elliptic curves over finite fields is highly suitable for communication between groups of corporate/government institutions.Example Consider an elliptic curve whose equation is y2 = x3 + 2x + 9. The graph of the function is shown in fig. (5b).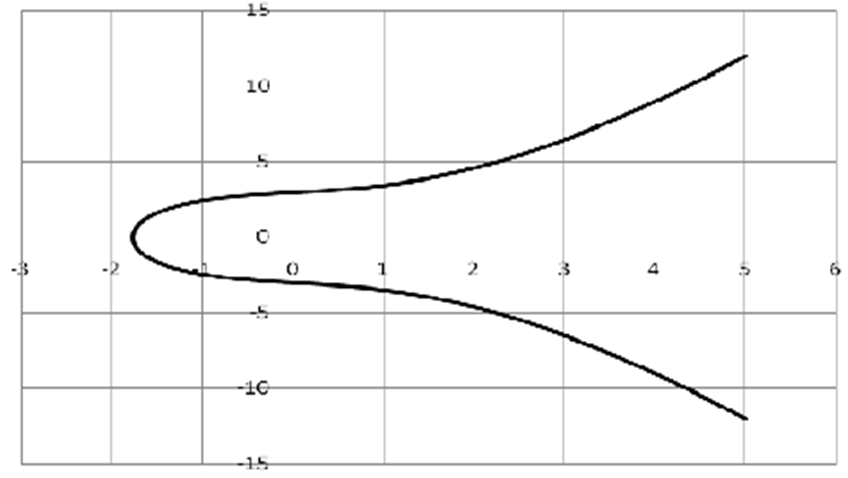 | Figure (5b). Elliptic curve equation y2 = x3 + 2x + 9 |
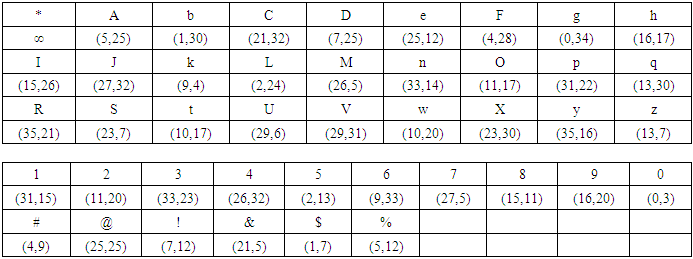
In the above graph the right lines can be drawn in xy-plane such that 1) there is no intersection between the right line and elliptic curve 2) the line intersects the elliptic curve at one point or two points or three points.Table (5a). Code table “Encryption of Data using Elliptic Curve over Finite Fields”
 |
| |
|
Now consider an elliptic curve (y2 = x3 + 2x + 9) mod 37, E37(2, 9). The points on the elliptic curve E37(2, 9) are{∞, (5,25), (1,30), (21,32), (7,25), (25,12), (4,28), (0,34), (16,17), (15,26), (27,32), (9,4), (2,24), (26,5), (33,14), (11,17), (31,22), (13,30), (35,21), (23,7), (10,17), (29,6), (29,31), (10,20), (23,30), (35,16),(13,7), (31,15), (11,20), (33,23), (26,32), (2,13), (9,33), (27,5), (15,11), (16,20), (0,3), (4,9), (25,25), (7,12), (21,5), (1,7), (5,12)}The graph of the function is shown in Figure (5c).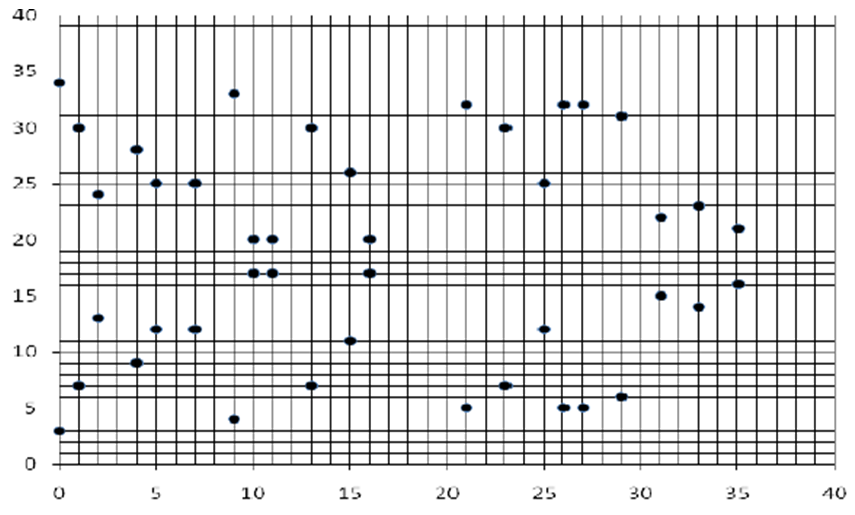 | Figure (5c). Elliptic Curve Group (Cyclic) E37(2, 9) |
Let C = (9,4). Alice selects a random number α = 5, any point A = (10,20) on the elliptic curve. She computes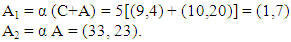 She keeps the random number α = 5 and the point A on the elliptic curve as her secret keys and publishes A1 and A2 as her public keys.Bob selects β = 7, B = (11, 20) on the elliptic curve. He computes
She keeps the random number α = 5 and the point A on the elliptic curve as her secret keys and publishes A1 and A2 as her public keys.Bob selects β = 7, B = (11, 20) on the elliptic curve. He computes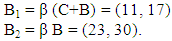 He keeps the random number β = 7 and the point B on the elliptic curve as his secret keys and publishes B 1 and B 2 as his public keys.Alice calculates AB = β B2 = (15, 11) and Bob calculates BA = β A 2 = (2, 13). Alice publishes AB as the specific public key for Bob and Bob publishes BA as specific public key for Alice.
He keeps the random number β = 7 and the point B on the elliptic curve as his secret keys and publishes B 1 and B 2 as his public keys.Alice calculates AB = β B2 = (15, 11) and Bob calculates BA = β A 2 = (2, 13). Alice publishes AB as the specific public key for Bob and Bob publishes BA as specific public key for Alice.
6.3.2.1. Encryption
If Bob wants to communicate the message ‘attack’ to Alice, Bob converts all the text characters of the message into the points on the elliptic curves using the agreed upon code table. 1). In the message ‘attack’ the first character ‘a’ corresponds to the point (5,25) using the code table. Bob selects a random number γ = 8 for encrypting the character ‘a’. Then the point (5,25) is encrypted asE1 = γ C = (1,30) which corresponds to the character ‘b’ in the conversion table. E2 = M + (β + γ) A1 –γ A2 + AB = (2,13) which corresponds to ‘5’ in the code table. So, the character ‘a’ in the plain text is encrypted to two characters {b,5} in the cipher text.2) ‘t’ is a point (10,17) in the code table. Let γ = 12E1 = (21,32) which corresponds to ‘c’ in the code table.E2 = M + (β + γ) A1 – γ A2 + AB = (2,24) which corresponds to ‘l’ in the code table. So, ‘t’ is encrypted as {c,l}.3) ‘t’ is a point (10,17) in the code table. Let γ = 19E1 = (4,9) which corresponds to ‘#’ in the code table.E2 = M + (β + γ) A1 – γ A2 + AB = (27,32) which corresponds to ‘j’ in the code table. So, ‘t’ is encrypted as {#,j}4) ‘a’ is a point (5,25) in the code table. Let γ = 2E1 = (29,31) which corresponds to ‘v’ in the code table.E2 = M + (β + γ) A1 – γ A2 + AB= (1,30) which corresponds to ‘b’ in the code table. So, ‘c’ is encrypted as {v,b}5) ‘c’ is a point (21,32) in the code table. Let γ = 3E1 = (1,30) which corresponds to ‘b’ in the code table.E2 = M + (β + γ) A1 – γ A2 + AB= (31,22) which corresponds to ‘p’ in the code table. So, ‘a’ is encrypted as{b,p}.6) ‘k’ is a point (9,4) in the code table. Let γ = 23E1 = (25,25) which corresponds to ‘@’ in the code table.E2 = M + (β + γ) A1 – γ A2 + AB = (4,28) which corresponds to ‘f’ in the code table. So, ‘k’ is encrypted as {@,f}Bob communicates {b,5; c,l; #,j; v,b; b,p; @,f }as the cipher text to Alice in public channel.
6.3.2.2. Decryption
Alice after receiving the cipher text {b,5; c,l; #,j; v,b; b,p; @,f} converts the cipher characters into the points (1,30), (2,13), (21,32), (2,24) (4,9), (27,32) (29,31) (1,30) (1,30) (31,22) (25,25) (4,28). She decrypts the message taking two points at a time as the points E1 and E2.1. M = E2 – (αE1 +α B1 + BA) = (5,25) which corresponds to the character ‘a’ in the code table.2. M = E2 – (αE1 +α B1 + BA) = (10,17) which corresponds t the character ‘t’ in the code table.3. M = E2 – (αE1 +α B1 + BA) = (10,17) which corresponds to the character ‘t’ in the code table.4. M = E2 – (αE1 +α B1 + BA) = (5,25) which corresponds to the character ‘a’ in the code table.5. M = E2 – (αE1 +α B1 + BA) = (21,32) which corresponds to the character ‘c’ in the code table. 6. M = E2 – (αE1 +α B1 + BA) = (9,4) which corresponds to the character ‘k’ in the code table. Then ‘attack’ is the original message.
7. Conclusions
Data confidentiality is important to protect data from unauthorized access of confidential information. In this research work we have implemented a new way for text encryption and decryption using which provides data confidentiality. For higher security with lesser key size, we use Elliptic curve in our research work.From the performance table, comparison table and security analysis section we can observe that our proposed algorithm has a lot of positive aspect. As Elliptic Curve Cryptography provides equal security like other cryptographic system but with less key size, it is very suitable for devices which have power, storage and processing limitation. So, our algorithm can be implemented in that device where less processing power and energy requires.
References
| [1] | William Stallings, ―Cryptography and Network Security, Principles and Practice‖, [Forth Edition], Pearson Education Inc., 2006. |
| [2] | Behrouza A. Forouzan and Debdeep Mukhopadhyay, ―Cryptography and Network Security‖, [Second Edition], McGraw Hill Education Private Limited, 2008. |
| [3] | Georgios Loukas and Gulay Oke, ―Protection against Denial of Service Attacks: A Survey‖, Oxford University Press, 2009. |
| [4] | Ross Anderson, Security Engineering: A Guide to Building Dependable Distributed Systems. The first edition (2001): http://www.cl.cam.ac.uk/~rja14/book.html. |
| [5] | Charles Daney, “Elliptic Curves and Elliptic Functions”, 1996, http://www.best.com/~cgd/home/flt/flt03.htm. |
| [6] | Laiphrakpam Dolendro Singh and Khumanthem Manglem Singh, Implementation of Text Encryption using Elliptic Curve Cryptography, ELSEVIER, ScienceDirect, Procedia Computer Science 54(2015) 73-82 (2015). |
| [7] | D. Sravana Kumar, CH. Suneetha and A. Chandrasekh AR, Encryption of Data using Elliptic Curve over Finite Fields, IJDPS Vol.3, No.1, January 2012. |
| [8] | S. Maria Celestin Vigila and K. Munesswaran, Implementation of Text based Cryptosystem using Elliptic Curve Cryptography, International Conference on Advance Computing, IEEE, pp. 82-85, December (2009). |



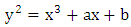 of the form. Each choice of numbers a and b yields different elliptic curves. The value of x, y, a and b may be from any field, namely complex number, real number, finite number and so on [5].
of the form. Each choice of numbers a and b yields different elliptic curves. The value of x, y, a and b may be from any field, namely complex number, real number, finite number and so on [5].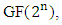 as shown in the following figure 3(a).Here Ep(a,b), e1 and e2 are public key and d is the private key of the receiver.
as shown in the following figure 3(a).Here Ep(a,b), e1 and e2 are public key and d is the private key of the receiver.
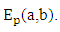 Algorithm
Algorithm 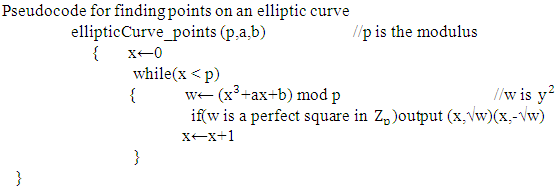 Example: Consider y2 = x3 + 2x + 3 (mod 5)
Example: Consider y2 = x3 + 2x + 3 (mod 5)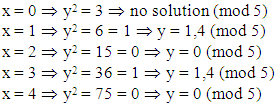 Then points on the elliptic curve are , (1,1) (1,4) (2,0) (3,1) (3,4) (4,0) and the point at infinity:
Then points on the elliptic curve are , (1,1) (1,4) (2,0) (3,1) (3,4) (4,0) and the point at infinity: 
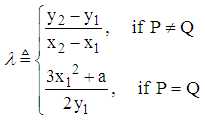
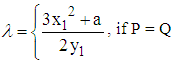 and x3 = λ2 - x1 - x2 mod p, y3 = λ (x1 - x3) - y1 mod p.
and x3 = λ2 - x1 - x2 mod p, y3 = λ (x1 - x3) - y1 mod p.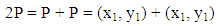 Since P=Q and x2 = x1, the values of λ, x3 and y3 are given by:
Since P=Q and x2 = x1, the values of λ, x3 and y3 are given by: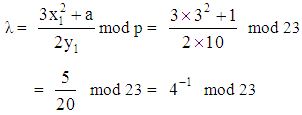 Considering,
Considering, 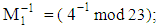 where,
where, 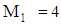 and m1 = 23Now using extended Euclidean formula:Here, quotient = q, remainder = r and t = t1 – qt2
and m1 = 23Now using extended Euclidean formula:Here, quotient = q, remainder = r and t = t1 – qt2 Since, r1 = 1So that,
Since, r1 = 1So that, 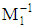 = t1 The extended Euclidean Algorithm gives t1 = 6. So, the multiplicative inverse
= t1 The extended Euclidean Algorithm gives t1 = 6. So, the multiplicative inverse 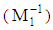 is 6 mod 23 =6.
is 6 mod 23 =6.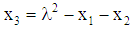 mod p = 62−3−3 mod 23 = 30 mod 23 = 7
mod p = 62−3−3 mod 23 = 30 mod 23 = 7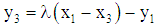 mod p = 6×(3−7)−10 mod 23 = −34 mod 23 = 12Therefore 2P = (x3, y3) = (7, 12).The multiplication kP is obtained by doing the elliptic curve addition operation k times by following the same additive rules.
mod p = 6×(3−7)−10 mod 23 = −34 mod 23 = 12Therefore 2P = (x3, y3) = (7, 12).The multiplication kP is obtained by doing the elliptic curve addition operation k times by following the same additive rules.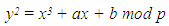
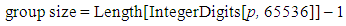

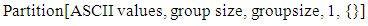
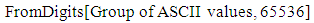
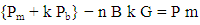
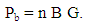
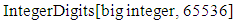
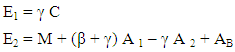 After encrypting all the characters of the message Bob converts the pair of points of each message point into the text characters using the code table. Then he communicates the cipher text to Alice in public channel.
After encrypting all the characters of the message Bob converts the pair of points of each message point into the text characters using the code table. Then he communicates the cipher text to Alice in public channel.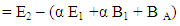 Decryption works out properly:-
Decryption works out properly:-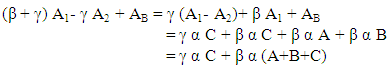
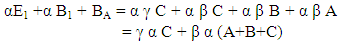
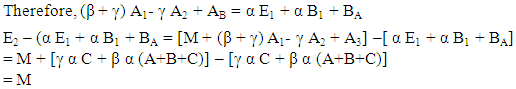 In this method a group of communicating parties A, B, C, D……. can communicate with one another securely, non- repudiatively in an authentic manner. Here each communicating party say X publishes two general public keys X1, X2. X also publishes a specific public key XY to be used by the communicating party Y for communication with Y. When Y wants to communicate with X, Y uses the general public keys of X (X1, X2), the specific public key published by X for Y (XY) and Y’s secret key y. To decrypt the message X uses Y’s general public keys (Y1, Y2), the specific public key published by Y for X (YX) and X’s secret key x. Here X creates specific public key XY for Y using Y’s public keys and X’s secret key. So, this method of encryption using elliptic curves over finite fields is highly suitable for communication between groups of corporate/government institutions.Example Consider an elliptic curve whose equation is y2 = x3 + 2x + 9. The graph of the function is shown in fig. (5b).
In this method a group of communicating parties A, B, C, D……. can communicate with one another securely, non- repudiatively in an authentic manner. Here each communicating party say X publishes two general public keys X1, X2. X also publishes a specific public key XY to be used by the communicating party Y for communication with Y. When Y wants to communicate with X, Y uses the general public keys of X (X1, X2), the specific public key published by X for Y (XY) and Y’s secret key y. To decrypt the message X uses Y’s general public keys (Y1, Y2), the specific public key published by Y for X (YX) and X’s secret key x. Here X creates specific public key XY for Y using Y’s public keys and X’s secret key. So, this method of encryption using elliptic curves over finite fields is highly suitable for communication between groups of corporate/government institutions.Example Consider an elliptic curve whose equation is y2 = x3 + 2x + 9. The graph of the function is shown in fig. (5b).

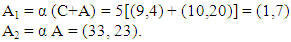 She keeps the random number α = 5 and the point A on the elliptic curve as her secret keys and publishes A1 and A2 as her public keys.Bob selects β = 7, B = (11, 20) on the elliptic curve. He computes
She keeps the random number α = 5 and the point A on the elliptic curve as her secret keys and publishes A1 and A2 as her public keys.Bob selects β = 7, B = (11, 20) on the elliptic curve. He computes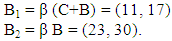 He keeps the random number β = 7 and the point B on the elliptic curve as his secret keys and publishes B 1 and B 2 as his public keys.Alice calculates AB = β B2 = (15, 11) and Bob calculates BA = β A 2 = (2, 13). Alice publishes AB as the specific public key for Bob and Bob publishes BA as specific public key for Alice.
He keeps the random number β = 7 and the point B on the elliptic curve as his secret keys and publishes B 1 and B 2 as his public keys.Alice calculates AB = β B2 = (15, 11) and Bob calculates BA = β A 2 = (2, 13). Alice publishes AB as the specific public key for Bob and Bob publishes BA as specific public key for Alice. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
