1. Introduction

Digital content access control is one of the key concerns in computer security today, and it is more important than ever before. A huge amount of digital data is constantly flowing through the internet, mobile networks, and cable and satellite televisions, and electronic medical data exchanged among large groups through public networks, especially in mobile environments, is especially vulnerable. In most cases, it is necessary to protect data from unauthorized and inappropriate access and changes by defining what information users can view and modify. Access criteria are generally associated with roles, groups, locations, or times. However, there are three main types of access control methods: Discretionary Access Control (DAC), Mandatory Access Control (MAC), and Non-Discretionary (Role-Based) Access Control (RBAC) [1]. Furthermore, access control methods are classified as military or commercial based on their usage. MAC is based on Bell-LaPadula’s 1973 multilevel security model, which is more concerned with confidentiality than integrity. In MAC, security policies are defined regardless of user operations. Thus, it is more suitable for military applications. On the other hand, DAC is the most used access control method. It is used in many operating systems, including UNIX, Windows 2000, and FreeBSD. The main disadvantage of DAC is the fact that its three-dimensional access control matrix has O(n2) growth. Finally, RBAC proposed by Ferraiolo and Kuhn in 1992 [1] blends MAC and DAC. It can be customized for individual applications regardless of policies [2-6].

In our case, we need to facilitate collaborative medical discussion over mobile devices where sensitive medical data, possibly large content, is shared through public networks while guaranteeing its C-I-A (Confidentiality, Integrity, and Availability) properties [3]. Moreover, we need to have a dynamic and flexible access control method to ensure the right access by the right user at the right time. However, there are no fixed access levels or roles for users. The one who initiates the communication becomes the coordinator of that session. Thus, s/he defines the access levels of the subordinates of the session. In another session, s/he can be a subordinate with low access privileges. Therefore, access control needs to be provided through the content. Moreover, we need to multicast the same content for multiple users with different access levels.

2. Background

Symmetric key cryptography is faster than asymmetric key cryptography mainly due to its small key sizes. However, it can only guarantee the confidentiality of the data. In a distributive environment, there are many security concerns, such as key distribution, authentication, authorization, integrity, and non-repudiation. To address such concerns, public key cryptography should be used. Therefore, in such scenarios, a combination of both symmetric and asymmetric key cryptography is being used to reap the benefits of both.

2.1. AES Cryptography

The Advanced Encryption Standard (AES), originally known as Rijndael, was introduced by Joan Daemen and Vincent Rijmen in 1998, and it was recommended by the National Institute of Standards and Technology (NIST) in late 2001 [7]. The AES is a symmetric-key block cipher with a fixed block size of 128 bits, and it uses keys of any multiples of 32 bits between 128 and 256. It is based on both substitution and permutation, and it is fast in both software and hardware implementations. The AES operates on a 4x4 column-major order matrix and has four main operations: AddRoundKey, SubBytes, ShiftRows, and MixColumns [8]. It has 10 to 14 cycles for each block based on its key size [9]. The SubBytes phase is a non-linear phase where it replaces each byte with a value in an 8-bit substitution box (s-box). In order to ensure good linear properties and avoid simple algebraic attacks, the s-box is constructed using the multiplicative inverse over Galois Field GF (2⁸). The time complexity of the Biclique attack, which is faster than the full brute force attack, is O(2ⁿ). Thus, given the present computational power, it is virtually unbreakable [10-13].

2.2. RSA Cryptography

Cryptosystems usually increase their key sizes to obtain higher security, and they can be as big as 300 digits or even bigger. Thus, it has become problematic to store them in small devices safely in public-key cryptography. In 1977, Ron Rivest, Adi Shamir, and Leonard Adleman introduced a public-key encryption method named RSA based on a mathematical problem called factorizing large integers where its time complexity is polynomial [14]. Currently, it is the public-key encryption method recommended by the NIST. However, it is being threatened by the rapid growth in computing power.

In 1999, a polynomial time algorithm for integer factorization and computation of discrete logarithms on quantum computers was discovered by Peter Shor [15]. This meant that once the quantum computers reached the 1000 Q-bit range, RSA could easily be broken. Recently, a few alternative approaches have emerged. Among them, Elliptic Curve Cryptography (ECC) has been promising due to its unique capabilities [6, 16-19].

2.3. ECC

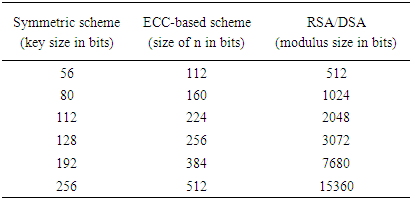
The new paradigm of public-key encryption using ECC was suggested independently by Neal Koblitz and Victor S. Miller in 1985 [14]. The main advantage of the ECC over RSA is its ability to provide equal security for significantly smaller key sizes. Thus, it provides the most security per bit of any known public-key scheme. Table 1 shows the equivalent security key sizes of ECC, RSA, and symmetric key cryptography. Although the computational overhead of both RSA and ECC grows as O (N³), where N is the key length in bits, ECC is more efficient and stronger than RSA. In fact, it is faster than all the other methods. Furthermore, it needs less computational power and less space. Hence, it is ideal for limited bandwidth communications, wireless devices, and PC cards [20-23].

Table 1. Comparable Key Sizes for Equivalent Security

ECC introduced a whole new algebra; thus, it is not vulnerable to common attacks. Instead of prime factorization or polynomial arithmetic, it uses Elliptic Curve (EC) arithmetic to perform computations. The security of ECC depends on the 1000-year-old unsolved mathematical problem called the Elliptic Curve Discrete Logarithm Problem (ECDLP), which refers to how difficult it is to determine k for a given kP and P. 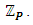The ECDLP problem appears to be much more difficult than the integer factorization problem and the discrete logarithm problem (DLP) of The order of 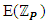is defined as 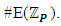According to Hasse’s theorem,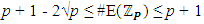 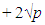[24]. The best known attack for ECC so far is Pollard’s rho attack, where it runs in exponential time, which is 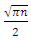[25].

The time complexity of RSA is sub-exponential, whereas it is exponential for ECC. Figure 1 shows the variation of the time complexities against the key sizes.

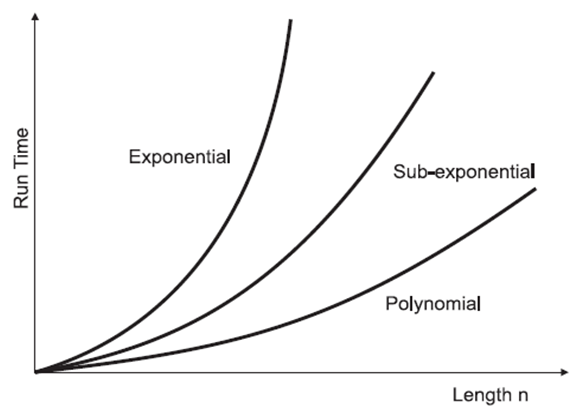Figure 1. Time complexity vs key size

The general equation for an EC is as follows:

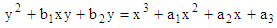ECs over real numbers use a special class of ECs of the form 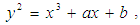also known as the Weierstrass equation of characteristic [24]. The discriminant of the polynomial 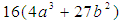should not be zero in order to possess three distinct roots for a given EC.

Furthermore, singular ECs are not suitable for cryptography, since they can be easily cracked due to the fact that they are isomorphic to either addition or multiplication. Super-singular ECs should also be avoided, since they are vulnerable to MOV attack. However, we cannot use real numbers for encryption, since they are prone to round-off error. Thus, we restrict the values of x and y to a prime finite field 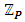. Such curves are denoted by the form of 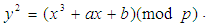Here, p is a prime, and p > 3. P is also known as the characteristic of the field. Further, the curve parameters 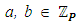should be carefully chosen to satisfy the condition 4a³ + 27b² ≠ 0 (mod p) [26]. However, when a finite field is chosen, pretty curves and lines are not applicable, yet the underlying algebra works as usual. When the curve is defined on a finite field 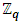with q elements, the number of points on the curve N, including the additive identity element O, is bounded by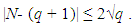

2.3.1. Point Addition

The point addition in ECs has nothing to do with the conventional arithmetical addition. It is the group operator for the points on an EC. Since it is commutative, EC forms an Abelian group. Let E be an EC over a field K, given by an equation 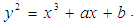We begin by defining a binary operation + on E(K). For a given P and Q ∈ E(K), the following equations can be used to compute a third point

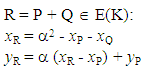where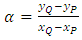

The point addition involves five subtraction operations, one addition, three modular multiplications, and one inversion operation. As shown in Figure 2, the EC has three adding cases. Case (a) shows the addition of two distinct points P and Q on the curve, whereas case (b) shows the adding of the point to itself. Finally, case (c) shows the adding of a point’s mirror or complement to itself in order to obtain the resulting point O at infinity.

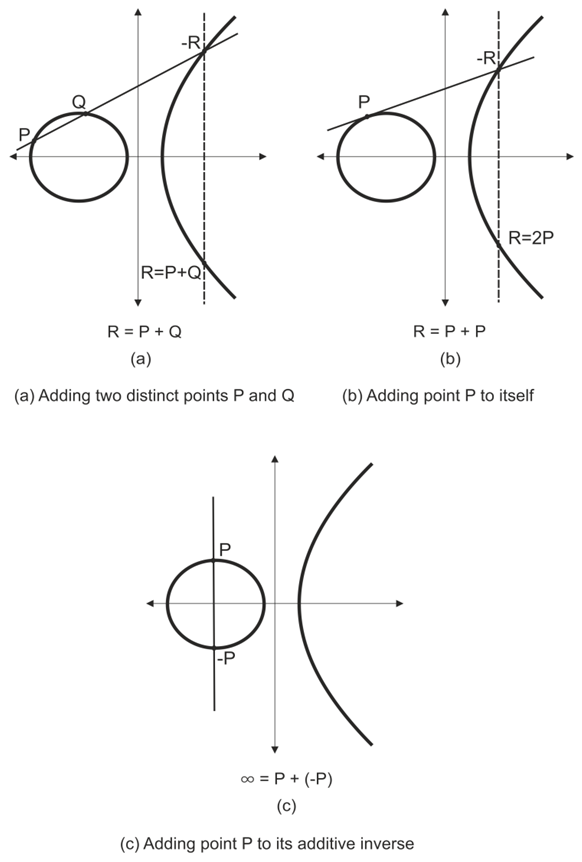Figure 2. Three adding cases in an EC

2.3.2. Point Doubling

Point doubling or scalar multiplication in ECs also does not represent conventional arithmetical multiplication. As we have seen above, if we extend the point addition to double a point P ∈ E(K), we can obtain a point R ∈ E(K) such that R = P + P = 2P by using the following equations:

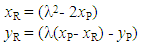where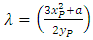

In ECC, scalar multiplication and inversion are very time-consuming operations. However, ECs have properties that enable the efficient implementation of scalar multiplication. For example, rather than computing 126P with 126 additions as follows:

126P = P + P . . . + P.

It can be calculated by six doublings and five additions as follows:

126P = 2(2(2(2(2(2P + P) + P) + P) + P) + P).

Further, the inverse addition or the subtraction of ECs is easy to compute. This can be further reduced to seven doublings and one subtraction as follows:

126P = 2(2(2(2(2(2(2P))))) - P).

Figure 3 shows the case of such consecutive point doubling in an EC. However, this scalar multiplication is the key to ECC. If we add point P, n times, a general case can be written as R = n.P ∈ E(K). This operation is elegant, as it is not easy to find the number n even though we know the points P, R, and the curve. Thus, n can be used as a secret or private key, whereas R together with P and the curve becomes its unique public key.

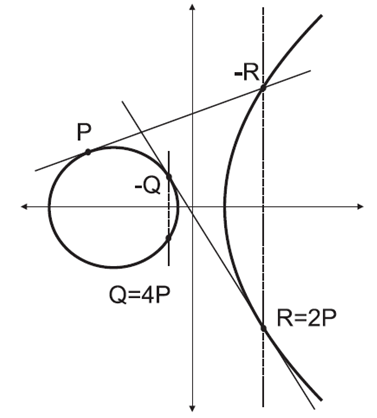Figure 3. Doubling point P repeatedly to find 4P

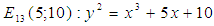Let p = 13 be a prime number and consider the EC . We obtain quadratic residues 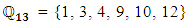from the reduced set of residues 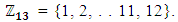This means that the valid points of the EC are as follows:

E₁₃(5; 10) = [(0 : 1 : 0); (0 : 6 : 1); (0 : 7 : 1); (1 : 4 : 1); (1 : 9 : 1); (3 : 0 : 1); (4 : 4 : 1); (4 : 9 : 1); (5 : 2 : 1); (5 : 11 : 1); (6 : 3 : 1); (6 : 10 : 1); (8 : 4 : 1); (8 : 9 : 1); (9 : 2 : 1); (9 : 11 : 1); (12 : 2 : 1); (12 : 11 : 1)]

The following commands can be used in SAGE to generate the valid points of 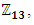as shown in Figure 4:

Figure 4. Valid points of Z13

SAGE: E=EllipticCurve(GF(13),[5,-3])

show (E.plot())

Let P = (5; 2) ∈ E₁₃(5; 10); Multiplicative values of P are as follows:

1*P = (5 : 2 : 1), 2*P = (0 : 7 : 1), 3*P = (9 : 2 : 1), 4*P = (12 : 11 : 1) , 5*P =(8 : 9 : 1), 6*P = (4 : 9 : 1), 7*P = (1 : 9 : 1), 8*P = (6 : 3 : 1), 9*P = (3 : 0 : 1), 10*P = (6 :10 : 1), 11*P = (1 : 4 : 1), 12*P = (4 : 4 : 1), 13*P = (8 : 4 : 1), 14*P = (12 : 2 : 1), 15*P = (9 : 11 : 1), 16*P = (0 : 6 : 1), 17*P = (5 : 11 : 1), 18*P =P*0= (0 : 1 : 0),19*P =1*P= (5 : 2 : 1), 20*P =2*P= (0 : 7 : 1)

2.3.3. Elliptic Curve Diffie-Hellman (ECDH) Key Exchange

The DH key-agreement scheme was proposed by Whitfield Diffie and Martin Hellman in 1976 [27]. The DH scheme is used to exchange secret keys between two or more parties. However, it is an interactive way of exchanging keys where the sender and the receiver need to be in the process at the same time. ECDH is the EC version of the DH scheme. If (P_A, S_A) and (P_B, S_B) are public and private keys of users U_A and U_B, respectively, where P_A and P_B are points on an EC, U_A and U_B can compute a secret key K as K_A = S_A × P_B by U_A and K_B = S_B × P_A by U_B [28, 29, 30]. According to the properties of ECDH,

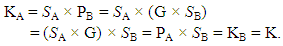
2.3.4. ElGamal Encryption using ECC

ElGamal encryption was proposed by Taher ElGamal in 1984 [31]. He was the first person to propose the idea of using a DLP for public-key cryptography. However, ElGamal encryption is a passive way of exchanging keys. In other words, the sender can encrypt the data off-line, and the receiver can decrypt it later. Assume that user U_B wants to send a secret key to user U_A; U_A chooses a random point α∈EC(a, b) and multiplies it by a random number S_A where 1≤S_A≤n-1 to find β such that β=α × S_A. S/he lets α and β be publicly known to everybody and secretly keeps S_A as his/her private key. U_B chooses a random point γ∈EC(a, b) and calculates C₁ such that C₁ = γ × α and C₂ such that C₂ = K + γ × β where K is the secret key s/he wants to share with U_A. U_B sends the message (C₁, C₂) to U_A, and U_A decrypts the message and gets the key K as follows [32, 33, 34].

K = C₂ – S_A × C₁.

2.3.5. Elliptic Curve Digital Signature Algorithm (ECDSA)

ECDSA is a variation of the digital signature algorithm that consists of two parts of the signature: sign₁ and sign₂. Let H be the hash value of the message, which is an integer, and k is a random number, sign₁ = (k × G)_x mod p. That means sign₁ only keeps the x-coordinate modulo p of k × G. If sign₁ = 0, then try another k. Now, sign₂ = k^-1(H + S_A. sign₁) mod p where k-1 is the multiplicative inverse of k modulo p, which is obtained by the extended Euclidean algorithm, and S_A is the private key of user A. When user B receives (sign₁, sign₂) along with the original document, s/he can compute the w = sign₂^-1 mod p, u₁ = H.w mod p, u₂ = sign₁.w mod p, and a point on the curve (x, y) = u₁ × G + u₂ × P_A where P_A is the public-key of user A. Now, s/he can verify the integrity of the message as well as the sender by comparing sign₁ ≡ x mod p. This method has been used by Bitcoin to verify whether the digital coins are spent by the right users. However, it is necessary to use a different k for each signature. For example, if the same k is used for two signs (sign₁, sign₂) and (sign₁’, sign₂’), k can be computed as sign₂ – sign₂’ = k^-1(H–H’). Finally, the secret key S_A can be computed by using the equation sign₂ = k^-1(H – S_A.sign₁). This technique was used to crack the Sony PlayStation 3 (PS3) in 2010 [35]. Moreover, it was used in an incident where the users of Android Bitcoin Wallet lost money due to faulty random number generators in August 2013 [36, 37, 38, 39].

2.3.6. Elliptic Curve Integrated Encryption Scheme (ECIES)

ECs cannot be directly used for encryption. Thus, in practice, they are combined with symmetric key algorithms and used as a hybrid scheme. In such cases, the EC is only used to encrypt the symmetric key that was used to encrypt the original data. ECIES is a combination of the Key Encapsulation Mechanism (KEM) and the Data Encapsulation Mechanism (DEM). The KEM is responsible for mapping a symmetric key to a point in the EC. The task of the DEM is to encrypt the plain text using the above symmetric key and authenticate the ciphertext [8, 23, 40].

2.3.7. Windows Media Digital Rights Management (WM-DRM)

Digital Rights Management (DRM) is associated with technologies and algorithms that help a content provider to enforce limitations, such as who can use the media content provided by them and in what way. ECC has been used for DRM for a while.

The Windows Media framework is a DRM that allows third-party vendors to create and distribute revenue-generating content. In WM-DRM, they use an EC-based encryption method to protect the access rights of their content, such as audio and video. It was a proprietary algorithm, and from 1999 to 2003, they released three versions of it. However, all three versions were compromised long ago. Other providers, such as Apple and Sony, have their own methods as well. According to Kerckhoffs’s principle, the secrecy of a cryptosystem should only depend on the key [41]. However, all these systems have been implementing security by hiding their algorithms [42, 43, 44, 45, 46].

2.3.8. Sony PlayStation

Sony’s PS3 console does not allow users to run codes that are not signed by one of its trusted parties. In other words, the developer first has to give his source code to some trusted party and get his signature on the binary. The Sony bootloader checks the signature before it executes the code. Sony has used ECC to implement its security mechanism where a secret key pair within the system is used to communicate with the license server. As we have explained above, the weakness of not avoiding the same random number twice enabled hackers to break it easily and pass their keys to others [35, 47].

3. Methodology

3.1. Symmetric Key Encryption

Although symmetric key encryption is faster, it requires a large number of keys in a multi-user environment. In particular, when the same content needs to be transferred to multiple users with different accessibility levels, payloads have to be encrypted for each user separately, which is very inefficient and time consuming. Therefore, in our proposed method, we first encrypt the content using a symmetric key and then encrypt the header separately for each user. The symmetric key encryption method is defined as ∏(E, D) where c←E_ki(p) and p←D_ki(c). Here, p represents the plain text, c represents the ciphertext, and k_i represents the symmetric session key of the i^th session. Further, E_ki and D_ki are the encryption and decryption algorithms, respectively, under the symmetric key k_i such that D_ki (E_ki (M)) = M. The AES is a well-tested, robust, and relatively efficient algorithm. As a result, we have selected it as our symmetric key algorithm. However, under the present hardware capabilities, its efficiency is insufficient for encrypting real-time video, even for videos of Phase Alternating Line (PAL) quality [13, 48].

3.2. Public-key Encryption

In this research, apart from ensuring confidentiality, we need to provide different access levels for each user separately. That is, for the same content, one user can edit it, whereas another can only read it. On the other hand, regarding another content, rights can be the opposite. Because of this dynamic nature, traditional role-based access control would not be an effective method.

In our approach, we define a public-key encryption method as follows:

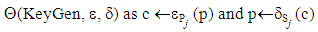Where ε and δ are the encryption and decryption algorithms, respectively, such that δ_Si (ε_Pi (M)) = M and δ_Pi (ε_Si (M)) = M to encrypt the secret symmetric key of the content.

ECC over a prime finite field has been chosen as the public-key encryption method. First, we define a prime finite field 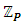to generate unique public and private key pairs (P_i, S_i) for all the users U_s = U₁, U₂, . . U_i. . . U_n in the system. Next, we define a base point or the generator G of the field, such that n × G = O for a large n. The EC, prime finite fields 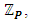and the base point G are publicly known to everybody in the system. Thus, each user U_i can choose a random number 1< k <(n-1) and multiply G, k times to get another point R in the curve such that R = k × G. This k becomes his/her private key S_i, whereas R, together with G, and EC become his public key P_i.

There are some vulnerable curves. Thus, the curve parameters p, a, and b should be chosen to define a suitable EC with higher robustness. If so, according to the properties of ECC, it would be difficult for an attacker to compute a user’s private key even s/he knows all the other information. However, in our first approach, we define different public and private key pairs {(P_i1, S_i1), . . (P_ij, S_ij)} for the same user U_i for his/her different accessibility levels L_i = { L _i1, L _i2, . . , L _ij }. In other words, if user U_A wants to send read-only content to user U_B, U_A uses U_B’s read-only public key P_Bread-only to encrypt the header of the document or the symmetric key. Hence, user U_B has to use his read-only private key S_Bread-only to get the symmetric key in order to open the document. Because we use our own application to view the content, decryption happens within the application. Therefore, user U_B will not be able to see the decrypted symmetric key.

However, managing a large number of key pairs for a single user is the biggest problem in this approach. Thus, we move to our second approach, which is defining the access-level key pairs associated to the master key pair. That means the application itself can generate a relevant access-level key pair once the user gives his/her master key. For example, in a public network, U_B can compute U_A’s read-only private key using U_A’s master key as P_Aread-only = P_Amaster× L_read-only where L_read-only is a constant for all users. On the other hand, U_A can compute his/her read-only private key as S_Aread-only= S_Amaster + L_read-only.

As a result, it is sufficient for a user to worry about managing a single key pair. In both approaches above, another issue is overlapping a user’s accessibility key with another’s master or access-level keys. To avoid such scenarios, two methods have been applied. One is to use a large key space with a high-order n to reduce the possibility of overlapping keys. The other is to use two key spaces ψ and 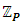for master keys and access-level keys separately. Because we need to use the same master key to compute access-level keys, the master key space ψ is defined in a subfield of the original field 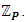However, in our second approach, there is a fixed relationship between a user’s master keys and his/her access-level keys. This gives more opportunities for an attacker to find one of his/her keys, which would thus compromise all of his/her keys.

In our third approach, we compute access-level keys in a random manner rather than a fixed association. This results in a different access-level key even for the same access level of the same user. For this, we used an extended version of the ElGamal encryption algorithm over the EC. U_A uses U_B’s public key to send a secret message X to U_B where X is another point on the curve.

For example, if U_A wants to send a read-only key to U_B, U_A selects a random number k and computes C₁ = G × k. Then, U_A computes C₂ = X_read-only + (k + L_read-only) × P_BMaster. Subsequently, s/he sends (C₁, C₂) to U_B where U_B finds the secret point X_read-only as in equation 1.

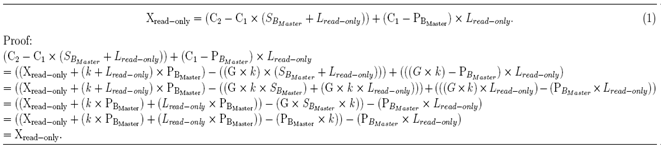Though we still use that fixed-number L_read-only, X_read-only becomes a one-time key due to the random number k.

Assume that U_A wants to send the symmetric key X to U_B under read-only permission. Consider the above E₁₃(5, 10) as our EC and take G = (5, 2) ∈ E₁₃(5, 10). Further, take the private keys of U_A and U_B as S_A = 5 and S_B = 10, respectively, by making their public keys P_AMaster= (8, 9) ∈ E₁₃(5, 10) and P_BMaster = (6,10) ∈ E₁₃(5, 10). Moreover, let L_read-only = 3 and the symmetric key X maps to the point X_{read-only =} (4, 4) ∈ E₁₃(5, 10).

Now, take 7 as the random number k between 1 and 17 and compute C₁ = G × k = (5, 2) × 7 = (1, 9) ∈ E₁₃(5, 10).

Then compute C₂ = (4, 4) + (7 + 3) × (6, 10) = (12, 11) ∈ E₁₃(5, 10). Once U_B receives (C₁, C₂) and L_read-only, s/he finds X_read-only = ((12, 11) – (1, 9) + (10 + 3)) + ((1, 9) – (6, 10)) × 3 = (4, 4) ∈ E₁₃(5, 10). However, this is only for a single user pair. Our fourth attempt is to extend this to a multicasting environment to avoid separate transmission for its users. Therefore, if the same content is shared with multiple users under different access rights, a single multi-casting can be used. However, this is simply done by concatenating multiple secret key encryptions to the header. Each encrypted field in the header can have a specific access right L_i regarding a specific user U_i. Finally, the application is responsible for implementing the required access control corresponding to the L_i where i represents the access rights, such as read-only, save, edit, etc. In other words, if the U_A wants to send an image for U_B with read-only permissions, U_C with save permissions, and U_D with edit permissions, U_A first needs to encrypt the image using AES symmetric key encryption. Then U_A needs to encrypt they AES key and IV using each receivers public key P_i and his/her access level L_i. For example, P_B with L_read-only, P_C with L_save, and P_D with L_edit. Structure of one such encrypted header is shown in the bottom diagram of the Figure 5. Next, these individual headers will concatenate as shown in the above diagram of the Figure 5. Finally find the digest of the whole message and sign using U_A’s private key. Once U_A multicast this to all the users, each user can verify the sender and the integrity of the message using message signature and the digest. Moreover, each can get their header and decrypt it. Because, the header has encrypted using the respective user’s public key, only that user will be able to decrypt it. Finally, the mobile application’s responsibility is to execute the received access rights for that user. For example, U_A’s app does not allow U_A to edit or save this image, whereas U_B can save the same image. Neither users nor apps have fixed access roles in the system. Access permission comes with the content and app dynamically adjusts to it.

3.3. File Structure

As shown in Figure 5, the file starts with the 1-byte field, which shows the sign size. Next, it contains the signature of the remaining part that is signed using the server’s private key. By verifying the signature, the application can confirm the integrity of the content as well as the sender. Because it is multicasting to several users with different access rights, there is a separate header for each user. The client application can find its header by checking the User ID. Then, it uses its private key together with access rights field L_i, C₁, and C₂ to decrypt the AES key.

Figure 5. File structure

Once the application obtains the symmetric key, it can decrypt the content and allow the user to perform the rights defined in the L_i.

3.4. Algorithms

Algorithm 1 shows the creation of the final encrypted file with access rights for multicasting.

Algorithm 1: File Encryption

Input: data file, sender’s public and private keys, receivers’ public keys, rights list L_i

Output: Encrypted file

1. Read file and compress the data

2. Randomly generate AES key and IV

3. Encrypt the data using AES key and IV

4. for i=1 to no of users do

5. Encrypt AES key and IV using receiver publickey[i] and rights L[i] and append to the encrypted file

6. Sign header and data using server’s private key and append to the encrypted file

7. end for

8. return: encrypted_file

Algorithm 2 shows the process of decryption for a given recipient.

Algorithm 2: File Decryption

Input: Encrypted file, receiver’s ID, receiver’s private key

Output: Decrypted file

1. Read the sign and verify the integrity.

2. Get the respective user’s header.

3. Decrypt the header using receiver’s private key and get the AES key and IV

4. Decrypt the data using AES key and IV

5. Decrypt the data file and create the decrypt_file.

6. return: decrypt_file

4. Results and Discussion

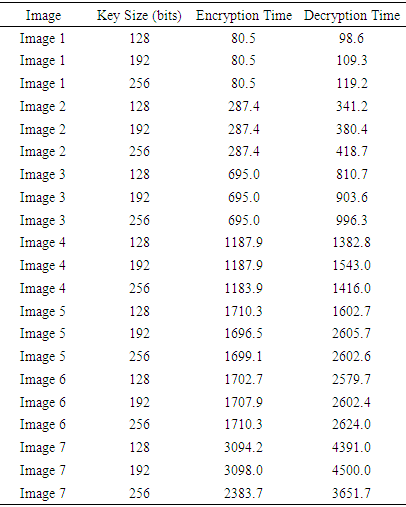
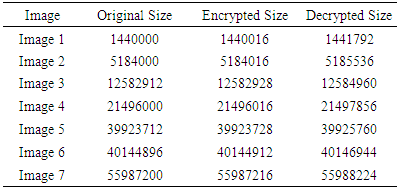
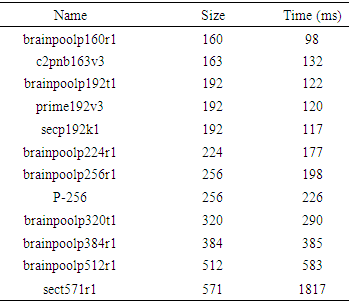
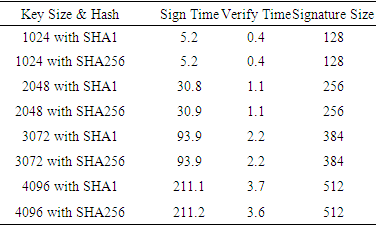
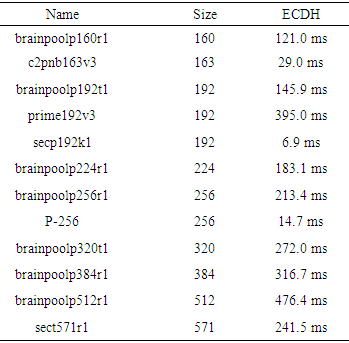
In order to identify efficient algorithms as well as bottlenecks, several algorithms were tested thoroughly. When the encryption of large medical images happens at the server side, it can be easily empowered by a high-performance server to increase its efficiency. However, the real bottleneck happens at the mobile device due to its limited resources. The mobile application was tested using Android 5.1 and a Samsung Galaxy Core Prime phone with 1.2 GHz Quad-core Cortex-A53 CPU, Adreno 306 GPU, and 1GB RAM.

As shown in Table 2, AES symmetric key encryption and decryption times are measured against the different image sizes and different key sizes. Because most of the processes running in the background are Worker Threads or AsyncTask, run times are significantly different from one run to another. Thus, each process is repeated 50 times, and the minimum time is taken as its best run time. The results show that it is almost the same in the long run for any key size. However, the IV generation time is significantly longer than the key generation time.

Table 2. AES Encryption and Decryption Times (ms)

Then, the AES encryption and decryption sizes and times are measured against the file sizes. PKCS5Padding is used as the padding method. According to the results shown in Table 2, the encrypted and decrypted sizes are slightly larger due to padding. These sizes are not dependent on the AES key size due to AES’s fixed block size of 128 bits for all its key sizes. As an enhancement, compression could be applied to remove coding redundancies prior to the encryption to reduce the file size and the encryption time. However, compression after encryption could compromise the strength of the algorithm, because it destroys the uniform distribution of the changes across the whole ciphertext [48].

Table 3 shows that the encryption and decryption times increase with the file size but do not depend on the key size. Decryption times are slightly longer than encryption times. Although the local and mobile network conditions are improving daily, network latencies significantly affect the run time. Thus, images are kept in the local storage.

Table 3. AES Encryption/Decryption Length vs File Size (bytes)

Next, we measured the run times of asymmetric encryption and decryption algorithms. While we chose ECC for the final system, RSA was also implemented to compare the results. Table 4 shows that the RSA key generation time increases exponentially as the key size increases.

Table 4. RSA Key Size vs Key Generation Time

One of the objectives of the research is to find the most optimal curve in terms of its key size, robustness, and run time to implement in a mobile device. Therefore, different key sizes are tested to compare its security against the run time. However, finding curve parameters for a secure curve is not as easy as one would think. To avoid the pitfalls of choosing vulnerable curves, the NIST-approved ECs together with ECC algorithms implemented in the Spongy Castle library were used. Other necessary parameters were taken from the Certicom documentation [49, 50].

According to Table 5, EC key generation time also increases with field size. However, sect571r1 is significantly longer.

Table 5. ECC Curve vs Key Generation Time

Table 6 and Table 7 show the sign and verification times and lengths for RSA and EC against different hash algorithms. It clearly shows that RSA sign lengths are significantly longer than EC sign lengths.

Table 6. RSA Sign and Verification Times (ms) and Sign Size (byte) Vs Hash Algorithm

Table 7. ECC Sign and Verification Times (ms) and Sign Size (byte) vs Hash Algorithm

Moreover, EC times are much better compared to respective RSA sign times. However, RSA takes significantly less time for verification. As before, sect571r1 is much slower compared to the other curves. Further, it shows that the sign and verification times do not depend on the hash algorithm.

Table 8 shows the DH key exchange times over EC and ElGamal encryption and decryption times over EC.

Table 8. Curve vs Run Time

As shown in Figure 6, some curves are significantly faster than the others, perhaps due to code optimizations, such as using the best methods to compute EC operations.

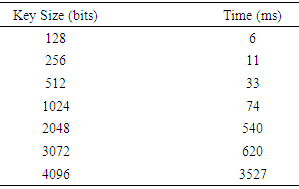
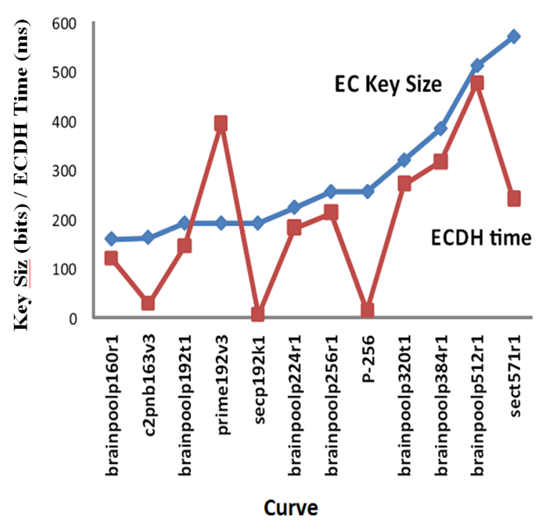Figure 6. ECDH time and key size

Theoretically, run time should increase as the key size increases. However, the results show that certain curves with high key sizes are faster than some of the curves with lower key sizes. This is mainly due to the code optimization of certain algorithms against the others.

Since the NIST’s smallest recommended key size is 224, developers have not put much effort into the optimization of smaller curves [51].

Furthermore, the expected run time of ECC is shorter than its equivalent secured RSA version. However, it is significantly longer due to the non-optimized implementation of ECC algorithms in the Spongy Castle library.

Unlike in symmetric key encryption, asymmetric key encryption alone cannot be used to encrypt data. Thus, it needs to be coupled with a symmetric key algorithm to be used for encryption. In the present work, we used ECIES for public-key encryption. Moreover, mismatches of implementations in java. security and Spongy Castle create some inconsistencies in the EC calculations, such as computing the wrong public key for a given private key and EC. As a result, key pairs may not be able to decrypt the content. According to Martinez et al., it is impossible to implement a software version of ECIES that is compatible with all standards [40]. The biggest barrier here is the Certicom patent for ownership of ECC. Thus, usage and development of ECC have become limited. Although Certicom provides advice on using their curves and parameters to obtain safe curves as well as to facilitate interoperability, Daniel and Tanja [52] have shown that most of those recommended curves are not safe. E382, M383, and Curve383187 are reported to be some of the latest safe curves.

Further, real-world attackers have used the gap between ECDLP difficulty and ECC security to compromise the security. Most of the attackers have broken systems without solving the ECDLP. They have used incorrect data for some rare curve points, branching time, and cache time to break systems. ECC has not yet been tested as thoroughly as RSA has for its robustness. Researchers have already found sub-exponential algorithms for certain parameters of ECC. Thus, crypt-analysts should explore it thoroughly to find its vulnerabilities.

Besides, it has already been proved that both RSA and ECC can be cracked with the use of Quantum computers in the future when they reach the 1000 Q-bit level.

One of the limitations of our approach is that again the application itself is responsible for implementing defined access levels. Decryption happens within the application and the user’s private key cannot be directly used to decrypt the symmetric key. Otherwise, once the symmetric key is obtained, the user can decrypt and use the content as s/he wishes. This can be avoided by implementing custom file structures for the content instead of using generic file structures. Besides, a suitable compression algorithm can be applied prior to the encryption to reduce the size of the content by eliminating the data redundancies. Another limitation is the inability to protect real-time videos due to the inefficiency of the AES.

5. Conclusions

In the present work, a combination of two robust cryptography methods has been used to implement a dynamic and flexible access control method that can ensure the access rights of sensitive medical data without compromising the strength of any. The method can be used to enforce different access rights for different users over the same content in a multicasting environment. It uses multiple keys effectively to enforce different access rights without making any extra key storage problem. The method is well suited to mobile devices, since ECC requires fewer computations and less space compared to other public-key methods.