1. Introduction

Measuring the quality of randomness of a given sequence is a crucial problem that significantly affects the quality of many practical applications such as distributed algorithms, cryptography [1, 2], statistical sampling and computer simulation, as example pseudo-random numbers used in Monte Carlo calculations [3]. In other words, the quality of such applications depends on generating unpredictable (random) sequence of quantities. From the practical point of view, such sequence must be of sufficiently large size in the sense that the probability of any particular value being selected must be sufficiently small in order to prevent an adversary from optimizing a search scheme based on such probability.

There are many techniques described in the literature for generating random, pseudorandom bits, parallel pseudorandom bits and numbers. A random bit generator is a device or an algorithm which outputs a sequence of independent and unbiased binary digits. A random bit generator can be used to generate uniformly distributed random numbers. However, generating of random bits is an inefficient procedure in most practical environments (storing and transmitting a large number of random bits are impractical if these are required in applications). We can overcome this difficulty by substituting a random bit generator with a Pseudorandom Bit Generator (PRBG).

In order to make sure that such generators are secure enough, they should be subjected to a variety of statistical tests designed to detect the specific characteristics expected of random sequences. We now review a number of empirical tests described in the literatures; for further details [4-7].

Runs Test tests the runs up and down or the runs above and below the mean by comparing the actual values to expected values. The statistic for comparison is the chi-square.

Frequency Test develops frequency distribution of individual samples, uses the chi-square test to compare the distribution of the set of numbers generated to a uniform distribution.

Poker Test (to be explained later in details) treats numbers grouped together as a poker’s hand. Then the hands obtained are compared to what is expected using the chi-square test [8, 9].

These sequential tests often check for correlations within a stream (on one processor), or the combined stream from all processors [10], while parallel tests check for correlations between different streams (on different processes) [11].

MATLAB is a wonderful high-level programming language for scientific research. It is an interactive environment that provides high-performance computational routines [12]. Since threads are a common software solution for parallel programming, on multi-core systems [13]. We found that MATLAB supports kinds of parallelism one of them is multithreaded parallelism [14].

MATLAB is an interpreted language, M-files execute slower than compiled programs written in other languages, such as C, C++, and Fortran. Therefore, we use MEX-file (MEX stands for MATLAB Executable), because when we integrate MATLAB with C++ code we can combine the advantages of MATLAB with the advantage of multithreading that increase speed. Moreover, the execution time of MEX files is significantly less than M-files [10, 15].

OpenMP (Open Multi-Processing) is an Application Program Interface (API) that supports multi-platform shared memory multiprocessing programming like C++. Moreover, OpenMP is a nice way to get a parallel program from a sequential program and it is standard for shared memory programming for scientific applications.

This paper is organized as follows. In Section 2, we discuss Poker test. In particular, two versions of Poker test are presented in the literatures, the classical Poker test and the modified Poker test. In Section 3, we run some experiments for Poker test in parallel with MATLAP followed by a discussion of the results. Finally, Section 4 we provide some final conclusions.

2. Poker Test

In this section we present in details the two versions of Poker test, the classical Poker test and the approximated Poker test.

2.1. Classical Poker Test

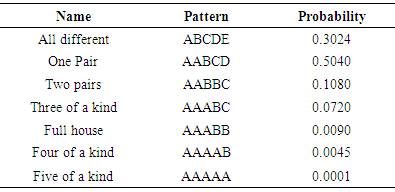
The classical poker test consists of using all possible categories obtained from poker that uses five hands, i.e. AAAAA (five of a kind), AAAAB (four of a kind), AAABB (full house), AAABC (three of a kind), AABBC (two pairs), AABCD (one pair), and ABCDE (bust). In general, the poker test using five hands considers n groups of five successive integers denoted by (X_5i, X_5i+1,…, X_5i+4), 0 ≤ i ≤ n, and then observes which of the seven possible patterns is matched by each quintuple. The following table summarizes such patterns and their corresponding probabilities.

It is well known that the number of hands a poker test can apply with is not restricted to five [5]. In particular, Poker test that uses four hands is more convenient to be applied to certain applications such as simulation(see [16]), and cryptography (see [2], [17]) in which we need to generate random integers or a random sequence of bits. For example, in cryptography, secret keys (used for encryption of messages or other purposes) are generated using random number generators (RNGs) (see [17]). Thus we applied Poker test to bit streams (typically represented by a 32-bit or 64-bit unsigned integer) rather than floating point numbers, and since 64 bits is not evenly divisible by five we use the closest number that divides 64: four. That is, the generated sequence of random numbers is divided into segments of four bits (see [18]).

Given a sequence of n random numbers to be tested, it is shown that there is a limit based on n as to how large the value of k can be [19]. On the other hand, most practical applications apply poker test with different values of k in order to ensure that the underlying sequence is truly random [20].

Some cryptographic algorithms using block cipher take blocks, or keys with different sizes 128, 192, or 256 bits. Therefore, if the block or the key size is 192, we find that they are not evenly divisible by five or four, however divisible by two. Therefore, series of pseudorandom numbers generated is divided into parts, each consisting of two bits. This encourages us to apply Poker test with hands of two numbers instead of hands of three, four or five numbers, especially in applications involving testing the randomness of a sequences of bit such as cryptography.

Motivated by increase speed of the test we also implemented the Poker test in parallel with MATLAB using MEX-file with one, two, three and four threads, reducing the execution time of the test (see [21]).

A Chi-square test is based on the number of quintuple in each category. We count the number of occurrences in each k-tuples, and then use a chi-square analysis against the theoretical probabilities to determine whether the stack represents a fair poker deck. We computed the theoretical probabilities of some categories two (k=2), three (k=3), five (k=4) and seven (k=5) categories (see [18, 22, 23, 24]).

2.2. Approximated Poker Test

At the time the classical Poker test is designed, checking the occurrences of these subsequences of length five using a computer program creates difficulties for the programmers as they have no one systematic similarity. This motivates constructing a simpler version of the classical test to overcome the programming difficulties involved.

A good compromise would simply be to count the number of distinct values in the set of five (see [6, 16]). Namely, corresponding to the classical Poker test that uses five hands we get five categories, 1different, 2different, 3 different, 4 different and 5 different. Thus, a finite time algorithms have been designed to implement such modified Poker test; see [4, 24].

This breakdown is easier to determine systematically, and the test is nearly as good. In general, we consider n groups of k successive numbers, and then count the number of k-tuples with r different values. A chi-square test is then made using the following probability of the existence of r different.

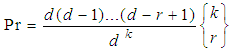Where 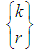denote the Stirling number of the second kind (see [25]) (the number of ways to partition a set of k elements into exactly r parts). The Stirling number can be computed using a well known formula.

Then different hands obtained can be compared to what is expected using the chi-square test to see how far the data has strayed from the theoretical distribution.

3. Experimental Results

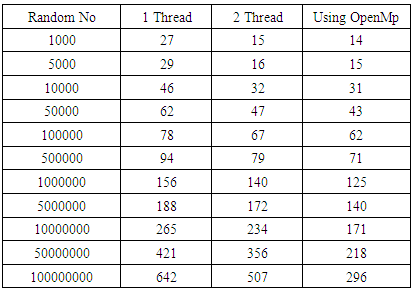
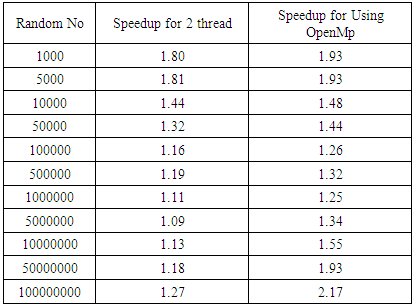
In this section we implement the classical Poker test in parallel with MATLAB using MEX-file with multithreading and the corresponding modified version using parallel MATLAB with OpenMP. We evaluate both versions of the test by implementing programs using C++ code that create random numbers. After that, we use MATLAB using MEX-file to count the occurrence of these differences or count number of occurrences, then classified each to possible type of poker hand. Finally, it determines the chi-square. We have compared the classical Poker test in parallel with one, and two threads and compare the performance.

The experimental results are reported on Laptop Core i5 2.50 GHz CPU, 4GB of RAM, 3M of Cache and, MATLAB 8.1 (R2013a).

We analyze the running time of the classical Poker test described in Figure 2, using parallel MATLAB with OpenMP. We determine the running time of executing the algorithm (time is in milliseconds). The resulting running time is shown in the following table 1.

Table 1. Summary of execution time in ms, for the original Poker test using threads and Using OpenMp

The results of Table 1 (shown in Figure 1) imply there is a significant improvement in term of the running time in the case of applying the classical Poker test with one, two threads and using parallel MATLAB with OpenMP, especially when the number of random numbers is sufficiently large.

Finally, we compare the performance of the classical Poker test described in Figure 2, with one, and two threads with that using parallel MATLAB with OpenMP. We are interested in the speedup of execution time for implement of the classical Poker method in parallel. Speedup Formula:

Speedup (S_n) = T₁/T_n

Where S_n is the speedup experienced on n processors, T₁ is the execution time for the sequential implementation, and T_n is the execution time on n processors. We calculated the speedup using the last equation. The tests were performed on one, and two threads as shown in figure 1. The resulting speedup is shown in table 2.

Table 2. Speedup results for two threads and Using OpenMp for each random numbers using Poker test

From Table 2 and figure 1, we show that the speedup of the implement of the classical Poker test in parallel with MATLAB using two threads is greater than one thread. Furthermore, Poker approach that using parallel MATLAB with OpenMP is significantly greater than that using one and two threads.

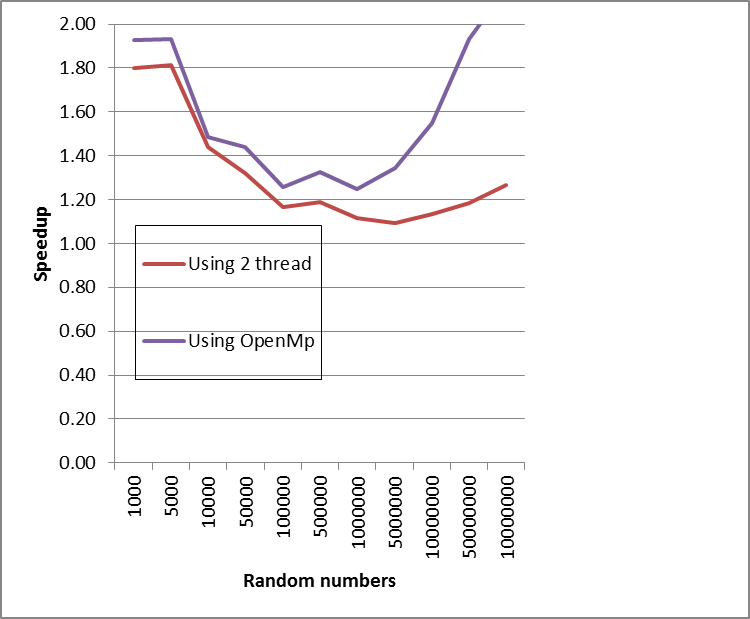Figure 1. Speedup gained by implementing the classical Poker test on two threads and Using OpenMp using parallel MATLAB

Figure 2. The classical Poker test pseudo-code algorithm

4. Conclusions

We have been studied Poker method for testing randomness using parallel MATLAB with OpenMP. In particular, we have been discussed the Poker using parallel MATLAB with OpenMP using MEX-file and compared the performance with parallel with MATLAB using MEX-file with one and two threads. From the computations point of view, we have been compared the performance of implemented the Poker test in parallel with MATLAB using MEX-file with multithreading.

We show that the speedups of implementing the Poker test using parallel MATLAB with OpenMP is significantly greater than that using MEX-file using multithreading with one and two threads, especially when the number of random numbers is sufficiently large.