Salah Sleibi Al-Rawi1, Ahmed Tariq Sadiq2, Belal Ghbeash Farhan3
1Information Systems Department, College of Computer , Anbar University, Ramadi-Anbar, Iraq
2Computer Science Department, University of Technology, Baghdad, Iraq
3Computer Science Department, College of Computer, Anbar University, Ramadi-Anbar, Iraq
Correspondence to: Salah Sleibi Al-Rawi, Information Systems Department, College of Computer , Anbar University, Ramadi-Anbar, Iraq.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper presents a proposed approach for assessing video quality without reference and makes use of a data hiding technique to embed a fragile mark into video frame by using Discreet Cosine Transform (DCT) and quantization. The fragile mark is random watermark generator using stream cipher based on Linear Feedback Shift Register (LFSR) and using Geffe generator to give a balanced distribution of zeros and ones in its output. The frame format consists of three color components, Red (R), Green (G) and Blue (B) for individual pixel, the watermark data should be hidden in Red (R) color channel to ensure the best recovery of the watermark . At the receiver, the mark is extracted from decoded video without any original reference video sequences. After extracted watermark, quality measure of the video is obtained by computing the degradation of the extracted mark. The results of this experiment indicate identical values of the Normalized Cross-correlation (NC) for three categories of real quality that have been proposed (good, low, bad) with the perceived quality. The experiment shows the error of the proposed system is 7% while correct ratio is 93% , the salt and pepper noise gives good results without errors while the Dust& Scratches noise gives highest error in the system. Results shown that the proposed algorithm provides a good estimation for the video quality when adding noise.
Keywords:
Video quality metric, digital watermarking , Geffe Generator, DCT, LFSR
Cite this paper:
Salah Sleibi Al-Rawi, Ahmed Tariq Sadiq, Belal Ghbeash Farhan, "Digital Video Quality Metric Based on Watermarking Technique with Geffe Generator", Computer Science and Engineering, Vol. 2 No. 7, 2012, pp. 138-146. doi: 10.5923/j.computer.20120207.03.
1. Introduction
The rapid spread of digital broadcasting has made it essential to develop technology that supports the operation and monitoring of video transmission. The field of digital data processing deals, in large part, with signals that are meant to convey reproductions and manipulations of visual information for human consumption. A visual data may go through many stages of processing before being presented to a human observer, and each stage of processing may introduce distortions that could reduce the quality of the final display[1]. Video Quality monitoring is becoming an important matter, especially due to the increasing transmission of multimedia contents over the internet and mobile networks. There are two metrics which are subjective metrics and objective metrics, The Subjective Quality Assessment (SQA) in which observers are asked to give their subjective assessment is the most reliable, but it is very expensive and can not be fulfilled in real time[2]. So the widely used assessment is Objective Quality Assessment (OQA). Objective Quality metrics are generally classified into the following categories based on the amount of information required about the reference video[3]:1) Full Reference metrics(FR)FR metrics model evaluates the performance of systems by making a comparison between the undistorted input, or reference, video signal at the input of the system, and the degraded signal at the output of the system at pixel level or frame level, i.e. the widely used Mean Square Error (MSE), Peak Signal-to-Noise Ratio (PSNR). It needs full original video sequence and can only be applied at the video encoder end.2) Reduced Reference metrics (RR)In RR metrics we do not have the reference video itself but we still have some limited information/data regarding the reference video. RR metrics are used in metrics that we have/need some information about the reference video but not all the reference video itself is to evaluate the quality of the video.3) No Reference metrics (NR)NR metrics are metrics which evaluate the quality of a video without any prior knowledge about the reference video. Objective NR quality metrics is a very difficult task. The human observers can rate the quality of a video without seeing its reference and just by observing the test video. In this paper, modified NR objective metric using data hiding with secure providing is proposed (called blind watermarking technique). The proposed approach makes use of a data hiding technique to embed a fragile mark into frames, Most video watermarking techniques today are derived from algorithms for still images. Therefore, we adopt a number of watermarking schemes for still images and apply them to each frame of a video sequence. Many watermarking methods for images have been proposed[4,5].Our proposed watermarking technique places focus on video, but can easily be expanded to other host media. Watermarking systems can be characterized by a number of properties ; the importance of each being dependent on the requirements of the specific application as well as the role in which the watermark plays[4].● Imperceptibility:The watermark embedded into the digital video sequence should be invisible to Human Vision System (HVS). This is one of the essential requirements for a watermark.● Robustness:Robustness means that the watermark cannot be destroyed unless the image (or signal) is altered to the extent of no value. Under the condition of imperceptibility, to implement a watermarking scheme with the robustness that can endure signal manipulations as much as possible is always a challenging task in digital watermarking. Therefore, robustness is an important feature for evaluating the performance of a watermarking scheme[6].● Capacity:Depending on the application, the watermarking algorithm should allow a predefined number of bits to be hidden.These properties are independent ,i.e., increasing the capacity will decrease the robustness or increase the visibility ,therefore it is essential to consider all these properties for evaluating of watermarking algorithm.
2. Related Work
2.1. Farias et al.(2004)[7]
The proposed algorithm uses a spread-spectrum algorithm to embed a data (binary image), called a watermark that consists of a binary sequence (can be a predefined pattern or a binary logo) , into video frames. At the receiver, the embedded data is extracted and a measure of its degradation is used to estimate the quality of the video. During embedding, this sequence is multiplied by a pseudo-random sequence with values in[-1;1], and the result is added the DCT domain of the image. The metrics used to evaluate quality are related to the square error (MSE and TSE) resulting from the difference between the extracted watermark signal and the reference mark signal (which is assumed to be known in the reception). The proposed metric provides a measure of the quality of a video based on a feature that we believe is relevant for the human observers: the motion. The metric is based on an unconventional use of a data hiding system. Simulation results indicate that the proposed quality metric is able to assess the quality of videos degraded by compression.
2.2. Brandao (2007)[8]
Described a technique whose purpose is to estimate the perceptual quality of DCT-based encoded images, without requiring the original data. To achieve this objective, a watermark is embedded in the DCT domain using a non-uniform quantization scheme. At the receiver side, the original DCT coefficients data distribution is estimated using a maximum likelihood approach. These distributions and the extracted watermark are then combined to estimate the error between reference and distorted DCT coefficients. This error is perceptually weighted, using a DCT domain perceptual model, allowing to blindly score the quality of the received media. Results have shown the effectiveness of the proposed algorithm when scoring the quality of images subject to lossy compression.
2.3. Chen et al.(2010)[9]
Some image and video processing algorithms can have the unintended consequence of introducing blocking artifacts into the processed imagery. Measuring blockiness plays an important role in many applications. The proposed method presented a reference-free blockiness measurement. For each frame , the absolute difference between horizontally adjacent pixels is computed, normalized, and averaged along each column. A one dimensional discrete Fourier transform is thereafter employed and a vertical blockiness measure is derived. A horizontal blockiness measure is computed similarly. Finally, a blockiness measure for the given image is formulated by pooling those two directional blockiness measures. The proposed method can accurately assess the blockiness without any a priori knowledge of the block origin and block size; therefore it is a blind measure. Experimental results show the effectiveness of the proposed method. The robustness of the proposed method is also justified.
2.4. Ouni et al.(2012)[10]
New NR metrics methods for color IQA are proposed. These methods are based on different statistical analyses and easy to calculate and applicable to various image processing. This proposed metrics are mathematically defined and overcome the limitations of existing metrics to assess the quality of the color in the image. The experiment results on various image distortion show that our proposed NR metrics have a comparable performance to the other traditional error summation metrics and to the leading metrics available in literature.
3. The Discrete Cosine Transform
Discrete Cosine Transform (DCT) is a general orthogonal transform for digital image processing and signal processing, with such advantages, as high compression ratio, small bit error rate, good information integration ability and good synthetic effect of calculation complexity and it is one of central technologies of image encoding and technical base used for several standards of multimedia video frequency compression (H. 261, H. 263 and MPEG, etc.). The DCT allows an image to be broken up into different frequency bands, making it much easier to embed watermarking information into the frequency bands of an image[11]. 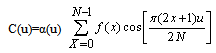 | (1) |
for u=0,1,2,3,4,…,N−1. Similarly, the inverse transformation is defined as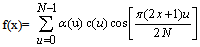 | (2) |
For x= 0,1,2,3,4…,N− 1 . In both equations (1) and (2) α(u) is defined as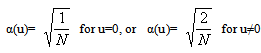 | (3) |
N is horizontal and vertical pixel number of pixel block, generally N=8. It is clear from (1) that for u = 0, 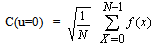 Thus, the first transform coefficient is the average value of the sample sequence. In literature, this value is referred to as the DC Coefficient. All other transform coefficients are called the AC Coefficients.The 2-D DCT is a direct extension of the 1-D case and is given by:
Thus, the first transform coefficient is the average value of the sample sequence. In literature, this value is referred to as the DC Coefficient. All other transform coefficients are called the AC Coefficients.The 2-D DCT is a direct extension of the 1-D case and is given by: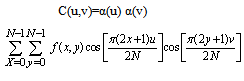 | (4) |
Where: u, v = 0,1,2,3,4,…,N −1 and. The inverse transform is defined as: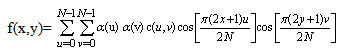 | (5) |
Where: x, y = 0,1,2,3,4,…,N −1.
4. Stream Cipher
Stream ciphers are an important class of encryption algorithms. They encrypt individual characters (usually binary digits) of a plaintext message one at a time, using an encryption transformation which varies with time. Stream ciphers can be either symmetric-key or public-key. stream ciphers are classified into two types: synchronous stream ciphers and asynchronous stream ciphers. The most famous stream cipher is the Vernam cipher, also called one-time pad, that leads to perfect secrecy (the ciphertext gives no information about the plaintext)[13].Stream ciphers have several advantages which make them suitable for some applications. Most notably, they are usually faster and have a lower hardware complexity than block ciphers. They are also appropriate when buffering is limited, since the digits are individually encrypted and decrypted. Moreover, synchronous stream ciphers are not affected by error-propagation[14].
4.1. Linear Feedback Shift Registers
Linear Feedback Shift Registers (LFSRs) are the most widely used building blocks for keystream generation in stream ciphers because of their very efficient hardware implementation, good statistical properties, large period, large linear complexity and ease of analysis using algebraic techniques. The secret key in these ciphers is the LFSRs initial state. Figure 1 depicts the general structure of an LFSR[15]. LFSRs are used in many of the key stream generators that have been proposed in the literature. There are several reasons for this[14]:1) LFSRs are well-suited to hardware implementation.2) they can produce sequences of large period.3)they can produce sequences with good statistical properties ; and4) because of their structure, they can be readily analyzed using algebraic techniques.A binary linear feedback shift register (LFSR) of size n is a finite state automaton with internal state of n bits. In each clock cycle, the update function L shifts the state by one position, where the input bit is a linear function of the previous bits. More precisely, let x=(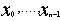 ) be the initial state. Then, the output sequence x=(
) be the initial state. Then, the output sequence x=(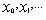 ) is determined by the recursion
) is determined by the recursion 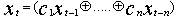 for t ≥ n, where all
for t ≥ n, where all 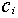 are fixed elements in {0, 1}[13].
are fixed elements in {0, 1}[13].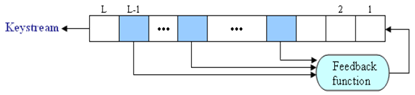 | Figure 1. General structure of a LFSR |
4.2. pseudo-random Sequences
Pseudo-random sequences have general sequences of 0s and 1s with some very specific statistical properties. These sequences are for instance used in spread-spectrum technologies, and in watermarking. the LFSR is a shift register with a certain number of memory elements, say p elements. Under the right conditions a shift register of p elements and with feedback through for instance a XOR function can create non-repeating sequences of 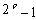 bits long. These sequences are known as maximum length sequences[16].
bits long. These sequences are known as maximum length sequences[16].
4.3. Nonlinear Combination Generators
One general technique for destroying the linearity inherent in LFSRs is to use several LFSRs in parallel. The keystream is generated as a nonlinear function f of the outputs of the component LFSRs (e.g. Geffe generator). The remainder of this subsection demonstrates that the function f must satisfy several criteria in order to withstand certain particular cryptographic attacks[14].
4.4. Geffe Generator
Geffe presented a generator based on a simple combination of three LFSRs as follows. Geffe’s generator consists of three LFSR’s connected as shown in Figure 2. The concept is to use LFSR2 as a control generator to connect either LFSR1 or LFSR3, but not both, to the output [17].The Geffe generator, is defined by three maximum-length LFSRs whose lengths L1, L2, L3 are pairwise relatively prime, with nonlinear combining function[14].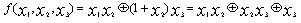 | (6) |
The keystream generated has period 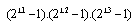 and linear complexity L=
and linear complexity L=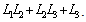
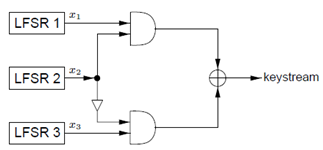 | Figure 2. The Geffe generator |
Although the complexity of this device could be greater in a different configuration of the stages, the generator does have some desirable attributes. For instance, it has a balanced distribution of zeros and ones in its output. It also offers the advantage of being useful as a module of a superstructure of similar arrangements, i.e., the entire generator of Figure 2. could play the role of LFSR1 in the same arrangement with like generators[17].
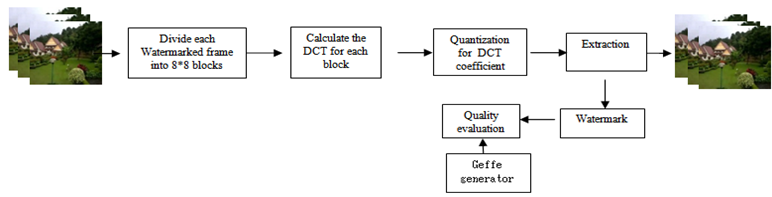
5. The Proposed System
There are many embedding methods which have been proposed in the literature. the data insertion can be done in the spatial domain, or in transform domain such as the DCT domain, and the Wavelet domain. The watermark bits are embedded in each 8*8 DCT block of the image. Figure 3. depicts the block diagram of the embedding system. The embedding algorithm needs to carefully choose where to embed the watermark bits in the 8*8 block. It is not wise to embed the watermark bits in the low frequency components of the DCT block, because these coefficients are subject to heavy quantization during JPEG compression. After embed the watermark for each frame in video , the video is generally compressed (MPEG, JPEG),then the video is transmitted .At receiver the watermark is extracted , by the comparison of retrieved watermark with the original watermark stored in the destination, then assesses how much video sequence quality degrades during compression and transmission, so as to achieve our goal to assess the video quality without reference. 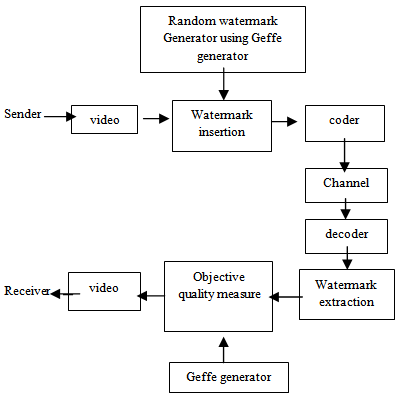 | Figure 3. Block diagram of the proposed system |
5.1. Random Watermark Generator
Random Watermark Generation used to get on security requirements for hidden process. The watermark can be obtained by stream cipher based of LFSR by using the Geffe generator which is one of the best pseudo random generators. Such as the random sequence with 0 as mean and 1 as variance. In this paper the random watermark generator will be 32*32 bit. Let the initial state is (10110110), the length m-sequence =8 bit. and max sequences is 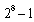 . The primitive polynomials with Geffe generator are :
. The primitive polynomials with Geffe generator are :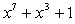 | (7) |
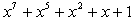 | (8) |
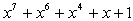 | (9) |
5.2. Embedding Process
The frame is partition into blocks of 8* 8 pixels where the watermark is embedded in the high frequency coefficients area to get on watermarked frame. the embed is based on the coefficients of FH region, the hiding “1” or “0” by using quantization function or directly without quantization to get on extracted watermark good in the coefficients of FH region. So the embedded binary watermark must be invisible to human eyes. each binary watermark pixel value (0 or 1) is embedded in one block of the frame, figure(4). The Embedding algorithm can be described in following steps:Step(1). Read the frame from video sequence ,The size of frame is 256*256 pixel.Step(2).generate random watermark ,the size 32*32 bit .Step(3).The original frame is divided into a number of blocks, the size of each block is 8*8. Step(4).Guarantee that the number of original frame blocks is equal to or greater than the number of watermark pixels.Step(5). For each frame block compute the DCT transform coefficients. Step(6).find the quantization(Q) of the DCT coefficient, using the following equation: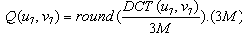 | (10) |
Where 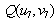 , is the quantized DCT coefficients ,
, is the quantized DCT coefficients , 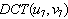 is DCT coefficient values, M is the embedding watermark strength=1,2,3,4.Step(7). each watermark pixel W (0 or 1) is embedded in the block(u ,v) as follow:
is DCT coefficient values, M is the embedding watermark strength=1,2,3,4.Step(7). each watermark pixel W (0 or 1) is embedded in the block(u ,v) as follow: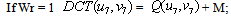 | (11) |
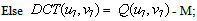 | (12) |
Where r=1,2,3,………… length of the watermark.Step(8). After embedding the watermark, IDCT transform is applied for each block, then the watermarked frame is reconstructed.
5.3. Extraction Process
Watermark detection techniques, which recover the watermark without resorting to the comparison between the watermarked and non-watermarked signals, are sometimes called oblivious or blind detection, otherwise they are called informed detection. To extract the watermark from watermarked image, the following steps are applied in figure5. Step(1).divided the watermarked frame into number of blocks 8*8.Step(2).calculate DCT transform coefficient for each block.Step(3).find the quantization(Q) of the DCT coefficient, using the quantization equation. Here M is the embedding watermark strength=4 only .Step(4). comparison the DCT coefficient with quantization result : | (13) |
Then Wr =0; Else Wr =1; Where r=1,2,3,………… length of the watermark.Step(5). Store W’, the recovered watermark.The error metrics used to test the proposed algorithm are Normalized Cross correlation (NC) and Peak Signal to Noise Ratio (PSNR), They are defined in[1,18].The NC is calculated between the original watermark W(k), and the extracted one W'(k) from this relation: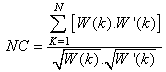 | (14) |
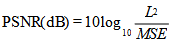 | (15) |
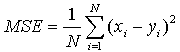 | (16) |
where N is the number of pixels in the image or video signal, and 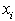 and
and 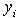 are the i-th pixels in the original and the distorted signals, respectively. L is the dynamic range of the pixel values. For an 8bits/pixel monotonic signal, L is equal to 255
are the i-th pixels in the original and the distorted signals, respectively. L is the dynamic range of the pixel values. For an 8bits/pixel monotonic signal, L is equal to 255
6. Experimental Results
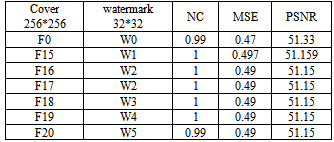
The performance of the proposed method for quality assessment is illustrated by testing a database of standard images and frames from video sequences . The distortion introduced for degrading the frame quality is a compression with quality factors(16) and additive noise . Due to its simplicity and popularity, the PSNR values are calculated accordingly and we evaluate the frame quality in terms of PSNR. The degradation of the recovered watermark can be used as a measure of the quality of the watermarked video by used NC . Video used in the evaluation process in our experiments is to be colored, video is split into number of frames (30 frame per second), hidden watermark will be in one of the basic components of the color frame (RGB) is the (R), we note by results that hidden process are good and without any distortions of the frames, where the embedded factor can take the values (1,2,3,4), the results that we obtained without exposure to (noise) of the process embedded the watermark in the video and the algorithm of extracted process indicate similar to the proportion of 99% -100%, Table 1. illustrates this.The figures 6,7 shows original frames and watermarked frames without noise, the calculate NC and PSNR after extraction of the watermark from the watermarked frames in tables 1,2.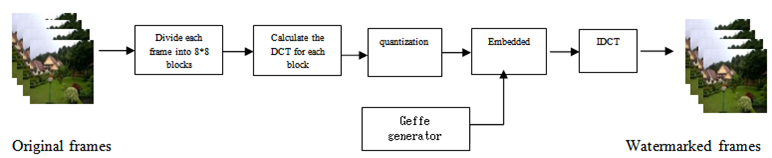 | Figure 4. Embedding Process |
 | Figure 5. Extraction Process |
 | Figure 6. Sample frame of original video ‘Indonesia', a. original frame , b. watermarked frame from video sequences. c. Extract the random watermark |
 | Figure 7. Sample frame of original video ‘Indonesia', a. original frame 15 , b. watermarked frame 15 from video sequences. c. Extract the random watermark |
Table 1. the result of embedded watermark and extracted watermark Without noise
 |
| |
|
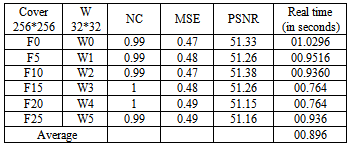
Table 2. show NC ,MSE, PSNR values and time to extract the watermark without noise
 |
| |
|
The Real time to extract watermark without noise for any frames, so time average shown in the figure 8. | Figure 8. show the time and time average to extract the watermark for some frames |
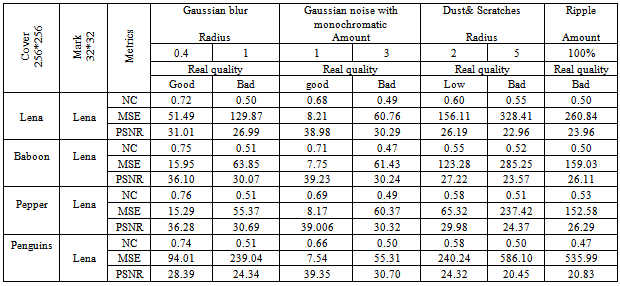
7. Performance of Proposed System Using Multiple Noise
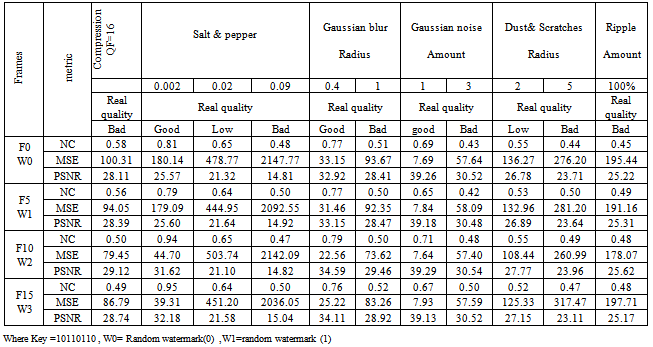
Here, we investigate the sensitivity of the proposed watermarking scheme for the following noise scenarios:(i) Salt-and-pepper noise (0.002,0.02,0.09).(ii) JPEG compression of quality factors 16%.(iii) Gaussian blur (0.4, 1).(iv) Gaussian noise with amount (1,3);(v) Distort Ripple(Amount=100%). The results obtained from various images and frames to calculate NC and PSNR , are shown in tables 3,4. According to the results in tables 3,4, the following rules shows the quality for the frames with various noise types.● If NC >0.65 then quality for frame is good.● If 0.53 < NC <=0.65 then quality for frame is low.● If NC <=0.53 then quality for frame is bad.Quality assessment using the NC of the extracted watermark, when the watermarked frames of video sequences with various noise types ,such as salt and pepper or ,jpeg compression , Gaussian blur, Gaussian noise, in table 4. We have evaluated the NC and PSNR of the distorted watermarked image or frames for each of the noise stated above. Real time for extraction process the watermark between (00.7332013 to 01.0296018 second). the relation between NC and MSE when add noise salt and pepper to frame (0),where decrease NC employ to increase MSE, as shown in figure 9.Table 3. calculate NC and PSNR for watermarked images with various noise types
 |
| |
|
Table 4. shows NC and PSNR of quality assessment for video
 |
| |
|
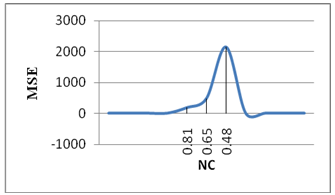 | Figure 9. illustrate the relation between NC and MSE when add noise salt and pepper to frame (0),where decrease NC employ to increase MSE |
 | Figure 10. a. Watermarked frame with noise salt and pepper(0.002), NC=0.95, refers to the real quality include classification of a is good . b. Watermarked frame with noise salt and pepper(0.02), NC=0.64 refers to the real quality include classification of b is low. c. Watermarked frame with noise salt and pepper (0.09), NC=0.50 , refers to the real quality include classification of (v) is bad . d. extract the random watermark from frame (15) after add noise(salt and pepper=0.002). e. extract the random watermark from frame (15) after add noise(salt and pepper=0.02). f. extract the random watermark from frame (15) after add noise(salt and pepper=0.09) |
When add noise salt and pepper to the watermarked frames, then real quality assessment will be by calculate NC as shown in figure 10. So the relation between MSE and NC of watermarked frame in figure11. Also the NC values for extracted watermark from some frames of video when add salt and pepper noise to frames with amount shown in table 3 are in figure 12.From the results which have obtained the six types of noise quantities (9) nine different values, applied to a database of 25 watermarked frames and image, show that the total noise is 9 * 25 = 225 noise type, and that the values of the NC have the error a small is (16) error of (225) noise type (the error is that depending on the value of NC may be the quality of the watermarked frame and image is one of the classification (low) while the originally image quality as perceived by the observer of the human classification (good) or may be the quality of the image of the classification (bad) While the quality of the image as seen by the human observer classification (low)), so the error rate is very low, 0.07approximately.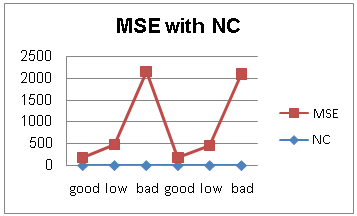 | Figure 11. show when increase MSE then NC will decrease in watermarked frames |
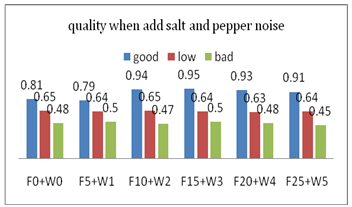 | Figure 12. illustrate the NC values for extracted watermark from some frames of video when add salt and pepper noise to frames with amount shown in table 3 |
8. Conclusions
A non reference objective video quality metric is proposed to estimate video quality in real time for multimedia system on the perceptual quality of digital video, the proposed algorithm does not require reference data, therefore called blind quality metric. The random watermark will be inserted into the video frames using DCT and uniform quantization, then extract the watermark from the video frames after transmission the video, the fragile mark is random watermark generator using stream cipher based on Linear Feedback Shift Register (LFSR) and using Geffe generator to give a balanced distribution of zeros and ones in its output. the fragile watermark extracted evaluate using Normalized Cross Correlation(NC) for known the distortion in watermark. The real time to extract the watermark is between (00.73-01.31 second),The results of this experiment indicate identical values of the (NC) for three categories of real quality that have been proposed (good, low, bad) with the perceived quality, the experiment shows that the error of the proposed system is 7% while correct ratio is 93% ,the better noise add gives result is salt and pepper while the more error is in Dust& Scratches noise. Results have shown that the proposed algorithm provides a good estimation for the video quality for adding noise.
References
| [1] | E. drelie “full-reference objective quality metrics for video watermarking, video segmentation and 3d model watermarking” Lausanne, ph.D thesis (2005) . |
| [2] | “Methodology for subjective assessment of the quality of television pictures,” Tech. Rep., ITU Recommendation BT.500-8, 1998. |
| [3] | S. Winkler: “Perceptual video quality metrics – a review.” in Digital Video Image Quality and Perceptual Coding, eds. H. R. Wu, K. R. Rao, chap. 5, CRC Press, 2005. |
| [4] | F. Hartung, and M. Kutter, “Multimedia Watermarking techniques”, July 1999. |
| [5] | M. Arnold, M. Schmucker, and S.D. Wolthusen, “Techniques and application of Digital Watermarking and Content Protection”, Eds. Northwood ,Artech House, 2003. |
| [6] | B. Furht, D.Kirovski.” Multimedia security handbook” p. cm. – (Internet and communications) .ISBN 0-8493-2773-3, 2005. |
| [7] | Mylène C. Q Farias, Marco Carli, Alessandro Neri, and Sanjit K. Mitra, “Video quality assessment based on data hiding driven by optical flow information”, Proc. Of SPIE Image Quality and System Performance, Vol. 5294, San Jose , January, 2004. |
| [8] | T. Brandão and M. P. Queluz,”blind perceptual quality assessment method for DCT based encoded images”, 15th European Signal Processing Conference, Poznan, Poland, September 3-7, 2007. |
| [9] | C. Chen , J. A. Bloom’’ A Blind Reference-Free Blockiness Measure’’ G. Qiu et al. (Eds.): PCM 2010, Part I, LNCS 6297, pp. 112–123, 2010. |
| [10] | S. Ouni, E. Zagrouba, M.Chambah,” A New No-reference Method for Color Image Quality Assessment”, February 2012. |
| [11] | J.Huang,Y.Q.Shi,“Embedding strategy for image watermarking in DCT domain” in Asia-Pacific Conference on Communications ,Vol.2 ,Beijing, China, pp. 981-984,Oct. 1999. |
| [12] | Haque, “A Two-Dimensional Fast Cosine Transform,” IEEE Transactions on Acoustics, Speech and Signal Processing, vol. ASSP-33 pp. 1532-1539, December 1985. |
| [13] | S. fischer ,”analysis of lightweight stream ciphers “, m.sc thesis 2008. |
| [14] | A. Menezes, P. van Oorschot and S. Vanstone,” Handbook of Applied Cryptography “1997 . |
| [15] | K.marton, A. suciu, I .Igant,” Randomness in Digital Cryptography: A Survey”,2010. |
| [16] | Peter Lablans, Ternarylogic LLC,” Generation of Pseudo-noise Sequences without LFSRs”, July 1, 2005. |
| [17] | S. Wei ,”On Generalization of Geffe’s Generator”, IJCSNS August 2006. |
| [18] | S. Bossi, F.Mapelli, R.Lancini, “Objective video quality evaluation by using semi-fragile watermarking”, Proc. of Picture Coding Symposium 2004. |

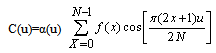
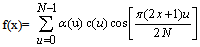
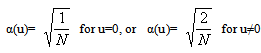
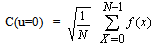 Thus, the first transform coefficient is the average value of the sample sequence. In literature, this value is referred to as the DC Coefficient. All other transform coefficients are called the AC Coefficients.The 2-D DCT is a direct extension of the 1-D case and is given by:
Thus, the first transform coefficient is the average value of the sample sequence. In literature, this value is referred to as the DC Coefficient. All other transform coefficients are called the AC Coefficients.The 2-D DCT is a direct extension of the 1-D case and is given by: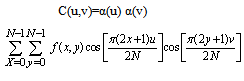
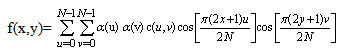
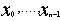 ) be the initial state. Then, the output sequence x=(
) be the initial state. Then, the output sequence x=(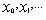 ) is determined by the recursion
) is determined by the recursion 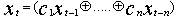 for t ≥ n, where all
for t ≥ n, where all 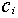 are fixed elements in {0, 1}[13].
are fixed elements in {0, 1}[13].
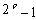 bits long. These sequences are known as maximum length sequences[16].
bits long. These sequences are known as maximum length sequences[16].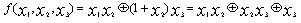
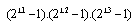 and linear complexity L=
and linear complexity L=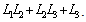


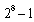 . The primitive polynomials with Geffe generator are :
. The primitive polynomials with Geffe generator are :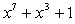
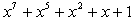
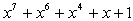
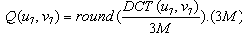
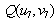 , is the quantized DCT coefficients ,
, is the quantized DCT coefficients , 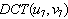 is DCT coefficient values, M is the embedding watermark strength=1,2,3,4.Step(7). each watermark pixel W (0 or 1) is embedded in the block(u ,v) as follow:
is DCT coefficient values, M is the embedding watermark strength=1,2,3,4.Step(7). each watermark pixel W (0 or 1) is embedded in the block(u ,v) as follow: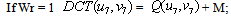
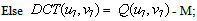

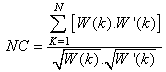
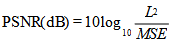
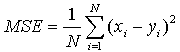
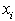 and
and 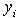 are the i-th pixels in the original and the distorted signals, respectively. L is the dynamic range of the pixel values. For an 8bits/pixel monotonic signal, L is equal to 255
are the i-th pixels in the original and the distorted signals, respectively. L is the dynamic range of the pixel values. For an 8bits/pixel monotonic signal, L is equal to 255







 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML



