-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Computer Science and Engineering
p-ISSN: 2163-1484 e-ISSN: 2163-1492
2012; 2(7): 129-132
doi: 10.5923/j.computer.20120207.01
Generalized Neutrosophic Set and Generalized Neutrosophic Topological Spaces
A. A. Salama1, S.A.Alblowi2
1Department of Mathematics and Computer Science, Faculty of Sciences, Port Said University, Egypt
2Department of Mathematics, King Abdulaziz University, Jeddah Saudi Arabia
Correspondence to: A. A. Salama, Department of Mathematics and Computer Science, Faculty of Sciences, Port Said University, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper we introduce definitions of generalized neutrosophic sets. After given the fundamental definitions of generalized neutrosophic set operations, we obtain several properties, and discussed the relationship between generalized neutrosophic sets and others. Finally, we extend the concepts of neutrosophic topological space [9], intuitionistic fuzzy topological space [5, 6], and fuzzy topological space [4] to the case of generalized neutrosophic sets. Possible application to GIS topology rules are touched upon.
Keywords: Neutrosophic Set, Generalized Neutrosophic Set, Neutrosophic Topology
Cite this paper: A. A. Salama, "Generalized Neutrosophic Set and Generalized Neutrosophic Topological Spaces", Computer Science and Engineering, Vol. 2 No. 7, 2012, pp. 129-132. doi: 10.5923/j.computer.20120207.01.
Article Outline
1. Introduction
- Neutrosophy has laid the foundation for a whole family of new mathematical theories generalizing both their classical and fuzzy counterparts, such as a neutrosophic set theory. The fuzzy set was introduced by Zadeh [10] in 1965, where each element had a degree of membership. The intuitionstic fuzzy set (Ifs for short) on a universe X was introduced by K. Atanassov [1, 2, 3] in 1983 as a generalization of fuzzy set, where besides the degree of membership and the degree of non- membership of each element. After the introduction of the neutrosophic set concept [7, 8, 9]. In this paper we introduce definitions of generalized neutrosophic sets. After given the fundamental definitions of generalized neutrosophic set operations, we obtain several properties, and discussed the relationship between generalized neutrosophic sets and others. Finally, we extend the concepts of neutrosophic topological space [9].
2. Terminologies
- We recollect some relevant basic preliminaries, and in particular, the work of Smarandache in [7, 8], Atanassov in[1, 2, 3] and Salama [9]. Smarandache introduced the neutrosophic components T, I, F which represent the membership, indeterminacy, and non-membership values respectively, where
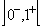 is nonstandard unit interval.Definition.[7, 8]Let T, I,F be real standard or nonstandard subsets of
is nonstandard unit interval.Definition.[7, 8]Let T, I,F be real standard or nonstandard subsets of  , with Sup_T=t_sup, inf_T=t_infSup_I=i_sup, inf_I=i_infSup_F=f_sup, inf_F=f_infn-sup=t_sup+i_sup+f_supn-inf=t_inf+i_inf+f_inf,T, I, F are called neutrosophic componentsDefinition [9]Let X be a non-empty fixed set.
, with Sup_T=t_sup, inf_T=t_infSup_I=i_sup, inf_I=i_infSup_F=f_sup, inf_F=f_infn-sup=t_sup+i_sup+f_supn-inf=t_inf+i_inf+f_inf,T, I, F are called neutrosophic componentsDefinition [9]Let X be a non-empty fixed set.  neutrosophic set (
neutrosophic set ( for short)
for short) 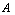 is an object having the form
is an object having the form 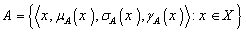 Where
Where 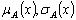 and
and 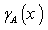 which represent the degree of member ship function (namely
which represent the degree of member ship function (namely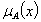 ), the degree of indeterminacy (namely
), the degree of indeterminacy (namely 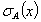 ), and the degree of non-member ship (namely
), and the degree of non-member ship (namely 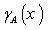 ) respectively of each element
) respectively of each element 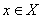 to the set
to the set 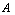 .Definition [9]. The NSS 0N and 1N in
.Definition [9]. The NSS 0N and 1N in 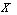 as follows:0N may be defined as:
as follows:0N may be defined as: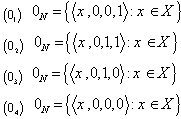 1N may be defined as:
1N may be defined as: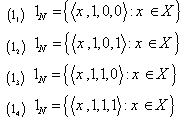
3. Generalized Neutrosophic Sets
- We shall now consider some possible definitions for basic concepts of the generalized neutrosophic set.DefinitionLet X be a non-empty fixed set.
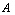 generalized neutrosophic set (G
generalized neutrosophic set (G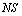 for short)
for short) 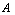 is an object having the form
is an object having the form 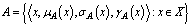 Where
Where 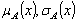 and
and 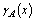 which represent the degree of member ship function (namely
which represent the degree of member ship function (namely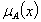 ), the degree of indeterminacy (namely
), the degree of indeterminacy (namely 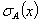 ), and the degree of non-member ship (namely
), and the degree of non-member ship (namely 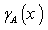 ) respectively of each element
) respectively of each element 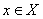 to the set where the functions satisfy the condition
to the set where the functions satisfy the condition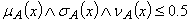 .RemarkA generalized neutrosophic
.RemarkA generalized neutrosophic 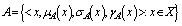 can be identified to an ordered triple
can be identified to an ordered triple 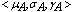 in
in 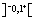 on.X, where the triple functions satisfy the condition
on.X, where the triple functions satisfy the condition 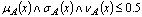 RemarkFor the sake of simplicity, we shall use the symbol
RemarkFor the sake of simplicity, we shall use the symbol 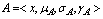 for the G
for the G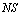
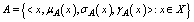 ExampleEvery GIFS
ExampleEvery GIFS 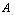 a non-empty set
a non-empty set 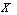 is obviously on GNS having the form
is obviously on GNS having the form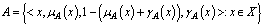 DefinitionLet
DefinitionLet 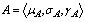 a GNSS on , then the complement of the set
a GNSS on , then the complement of the set 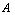
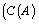 , for short
, for short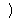 maybe defined as three kinds of complements
maybe defined as three kinds of complements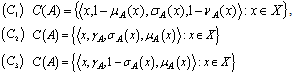 One can define several relations and operations between GNSS as follows:DefinitionLet
One can define several relations and operations between GNSS as follows:DefinitionLet 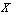 be a non-empty set, and GNSS
be a non-empty set, and GNSS 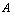 and
and 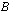 in the form
in the form 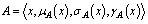 ,
, 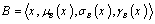 , then we may consider two possible definitions for subsets
, then we may consider two possible definitions for subsets 
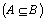 may be defined as
may be defined as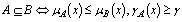 and
and 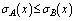
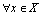
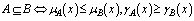 and
and 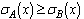 PropositionFor any generalized neutrosophic set
PropositionFor any generalized neutrosophic set 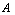 the following are holds
the following are holds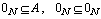
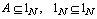 DefinitionLet
DefinitionLet 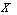 be a non-empty set, and
be a non-empty set, and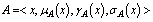 ,
, 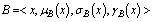 are GNSS Then
are GNSS Then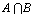 maybe defined as:
maybe defined as: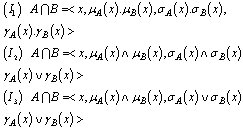
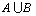 may be defined as:
may be defined as: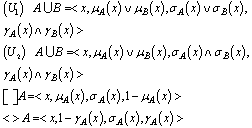 Example.3.2. Let
Example.3.2. Let 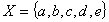 and
and 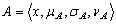 given by:
given by: 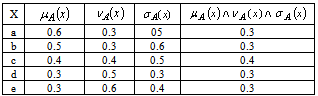 Then the family
Then the family 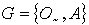 is an GNSS on X.We can easily generalize the operations of generalized intersection and union in definition 3.4 to arbitrary family of GNSS as follow:DefinitionLet
is an GNSS on X.We can easily generalize the operations of generalized intersection and union in definition 3.4 to arbitrary family of GNSS as follow:DefinitionLet 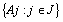 be a arbitrary family of
be a arbitrary family of 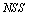 in
in 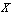 , then
, then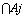 maybe defined as:1)
maybe defined as:1) 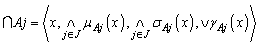 2)
2) 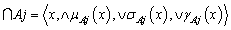
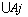 maybe defined as:1)
maybe defined as:1) 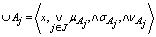 2)
2) 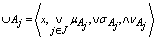 DefinitionLet
DefinitionLet 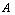 and
and 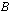 are generalized neutrosophic sets then
are generalized neutrosophic sets then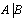 may be defined as
may be defined as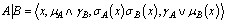 PropositionFor all
PropositionFor all 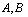 two generalized neutrosophic sets then the following are truei)
two generalized neutrosophic sets then the following are truei) 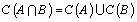 ii)
ii) 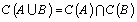
4. Generalized Neutrosophic Topological Spaces
- Here we extend the concepts of and intuitionistic fuzzy topological space [5, 7], and neutrosophic topological Space [ 9] to the case of generalized neutrosophic sets.DefinitionA generalized neutrosophic topology (GNT for short) an a non empty set
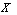 is a family
is a family 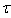 of generalized neutrosophic subsets in
of generalized neutrosophic subsets in 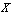 satisfying the following axioms
satisfying the following axioms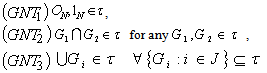 In this case the pair
In this case the pair 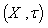 is called a generalized neutrosophic topological space (G
is called a generalized neutrosophic topological space (G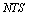 for short) and any neutrosophic set in
for short) and any neutrosophic set in 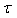 is known as neuterosophic open set (
is known as neuterosophic open set (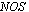 for short) in
for short) in 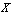 . The elements of
. The elements of 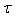 are called open generalized neutrosophic sets, A generalized neutrosophic set F is closed if and only if it C (F) is generalized neutrosophic open. Remark A generalized neutrosophic topological spaces are very natural generalizations of intuitionistic fuzzy topological spaces allow more general functions to be members of intuitionistic fuzzy topology.ExampleLet
are called open generalized neutrosophic sets, A generalized neutrosophic set F is closed if and only if it C (F) is generalized neutrosophic open. Remark A generalized neutrosophic topological spaces are very natural generalizations of intuitionistic fuzzy topological spaces allow more general functions to be members of intuitionistic fuzzy topology.ExampleLet 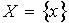 and
and Then the family
Then the family 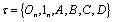 of G
of G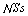 in
in 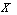 is generalized neutrosophic topology on
is generalized neutrosophic topology on 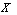 ExampleLet
ExampleLet 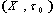 be a fuzzy topological space in Changes [4] sense such that
be a fuzzy topological space in Changes [4] sense such that 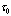 is not indiscrete suppose now that
is not indiscrete suppose now that 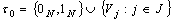 then we can construct two G
then we can construct two G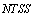 on
on 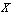 as follows
as follows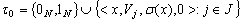
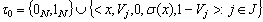 PropositionLet
PropositionLet 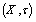 be a GNT on
be a GNT on 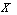 , then we can also construct several GNTSS on
, then we can also construct several GNTSS on 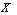 in the following way:a)
in the following way:a) 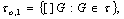 b)
b) 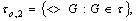 Proof a)
Proof a) 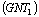 and
and 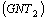 are easy.
are easy.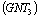 Let
Let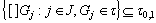 .Since
.Since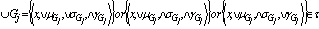 , we have
, we have 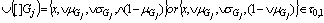 This similar to (a)DefinitionLet
This similar to (a)DefinitionLet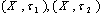 be two generalized neutrosophic topological spaces on
be two generalized neutrosophic topological spaces on 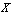 . Then
. Then 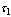 is said be contained in
is said be contained in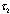 (in symbols
(in symbols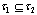 ) if
) if 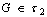 for each
for each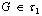 . In this case, we also say that
. In this case, we also say that 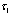 is coarser than
is coarser than 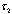 .PropositionLet
.PropositionLet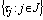 be a family of
be a family of 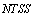 on
on 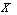 . Then
. Then 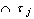 is A generalized neutrosophic topology on
is A generalized neutrosophic topology on 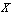 .Furthermore,
.Furthermore, 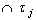 is the coarsest NT on
is the coarsest NT on 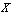 containing all.
containing all. 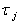 , sProof. ObviousDefinitionThe complement of
, sProof. ObviousDefinitionThe complement of 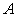 (C (A) for short) of
(C (A) for short) of 
 is called a generalized neutrosophic closed set (G
is called a generalized neutrosophic closed set (G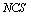 for short) in
for short) in 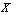 .Now, we define generalized neutrosophic closure and interior operations in generalized neutrosophic topological spaces:DefinitionLet
.Now, we define generalized neutrosophic closure and interior operations in generalized neutrosophic topological spaces:DefinitionLet 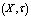 be G NTS and
be G NTS and 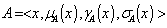 be a G
be a G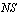 in
in 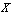 .Then the generalized neutrosophic closer and generalized neutrosophic interior of Aare defined by G
.Then the generalized neutrosophic closer and generalized neutrosophic interior of Aare defined by G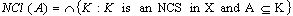 G
G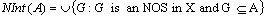 .It can be also shown that It can be also shown that
.It can be also shown that It can be also shown that 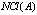 is
is 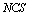 and
and 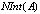 is a G
is a G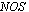 in
in 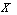
 is in
is in 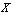 if and only if G
if and only if G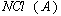 .
.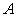 is Gin
is Gin 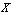 if and only if G
if and only if G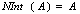 .PropositionFor any generalized neutrosophic set
.PropositionFor any generalized neutrosophic set 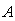 in
in 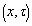 we have(a) G
we have(a) G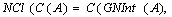 (b) G
(b) G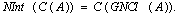 Proof.Let
Proof.Let 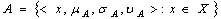 and suppose that the family of generalized neutrosophic subsets contained in are indexed by the family if G
and suppose that the family of generalized neutrosophic subsets contained in are indexed by the family if G contained in are indexed by the family
contained in are indexed by the family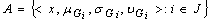 . Then we see that
. Then we see that 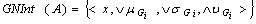 and hence
and hence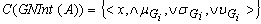 . Since
. Since 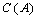 and
and 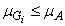 and
and 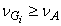 for each
for each 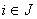 , we obtaining
, we obtaining 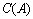 . i.e
. i.e 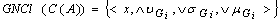 . Hence
. Hence 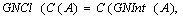 follows immediately This is analogous to (a).PropositionLet
follows immediately This is analogous to (a).PropositionLet 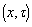 be a G
be a G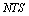 and
and 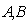 be two neutrosophic sets in
be two neutrosophic sets in 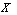 . Then the following properties hold:
. Then the following properties hold: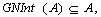
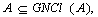
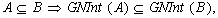
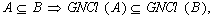
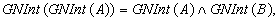
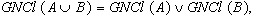
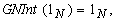
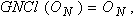 Proof (a), (b) and (e) are obvious (c) follows from (a) and Definitions.
Proof (a), (b) and (e) are obvious (c) follows from (a) and Definitions.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML