-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Computer Science and Engineering
p-ISSN: 2163-1484 e-ISSN: 2163-1492
2012; 2(5): 77-85
doi: 10.5923/j.computer.20120205.06
New Chaos-Based Image Encryption Scheme for RGB Components of Color Image
Nashwan A. Al-Romema 1, Abdulfatah S. Mashat 2, Ibrahim AlBidewi 2
1Faculty of Computing and Information Technology- Rabigh
2Faculty of Computing and Information Technology- Jeddah, King Abdulaziz University, P.O. Box 344, Rabigh 21911, Saudi Arabia
Correspondence to: Nashwan A. Al-Romema , Faculty of Computing and Information Technology- Rabigh.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The widely use of data digitization leads to the necessity of hiding the content of a message when it enters an insecure channel. The message prepared by the sender is encrypted before transmission. The encryption process requires an encryption algorithm and a key. In image cryptography, recently numbers of effective chaos-based image encryption schemes have been proposed. This paper presents a novel image encryption scheme which encrypts the pixels' RGB component instead of the pixels itself, where every pixel in the image will be extracted to its RGB triple, encrypted, and prepared to be transmitted. In the encryption process we use another image as a key, this image should be larger than or of the same size of the plain image that we intend to encrypt. The image encryption scheme introduced is based on chaotic systems. Simulation results show that the proposed image encryption scheme achieves high level of security, and reduces the encryption and the decryption time of image data.
Keywords: Image RGB Color Components, Image Encryption, Chaos-Based Encryption, Chaotic Maps
Article Outline
1. Introductions
- Hiding the content of data that are sent over an insecure channel has become one of the most important processes of some applications[1]. The message prepared by the sender is encrypted by using the encryption algorithm and key. In image cryptography, the focus has been putonsteganography, and in particular on watermarking during the last years[2]. Steganography is the science of hiding information and does not involve key[9]. The security of multimedia data in digital distribution networks is commonly provided byencryption, which is the mathematical process that transforms a plaintext message into unintelligible ciphertext (confused). The classical image encryption such as Data Encryption Standard (DES) is designed with good confusion and diffusion properties[5], but it has the weakness of low-level efficiency when the image is large[10]. Classical and modern ciphers have all been developed for the simplest form of multimedia data. Chaos-based image encryption scheme is one of the encryption algorithms that have suggested a new and efficient way to deal with fast and highly secure image encryption[10]. Encrypting images, using chaos-based image encryption scheme, considers the image as 2-dimensional array of pixels[5]. Fridrich[8] suggested that a chaos-based image encryption processesgo through two processes, i.e 1-chaotic confusion, and 2-pixel diffusion. In chaotic confusion process, the pixels of plain image are permuted with a 2 dimensional chaotic map, whereas the pixel diffusion alternates the value (gray-level) of each pixel in a sequential manner. Based on this architecture a number of chaos-based image encryption schemes have been proposed. Chen et al. employed a three-dimensional (3D) cat map[12] for image encryption. Guan et al.[11] used a two-dimensional (2D) cat map for pixel position permutation and a chaotic system that is called “The discretized Chen’s chaotic system” for pixel value masking. Wong et al.[5] proposed an idea to accelerate the encryption speed of the chaos-based image encryption schemes proposed by Lian et al.[7], in which the typical structure of chaos-based image encryption schemes is structured as the shown in figure 1. Each research in this area came up with a different algorithm of key generation and improvement of the chaotic encryption in terms of security and speed. Some algorithms proposed different ways of encryption by using hyper-chaotic to confuse the relationship between the plain-image and ciphered image[15]. All of these algorithm use one-dimension, two-dimension or three-dimension chaotic map with the advantage of high-level of efficiency. But their weaknesses materialize in the limitation of the key space used in chaotic system[1], and the complicated algorithm that includes large number of computer operations which might affects the performance of encryption/decryption processes. In addition to that the initial key values which might be easy for brute-force attack to predict. The generation of the key during encryption/decryption process, also affect the performance of the algorithm since you need to run different operations for this purpose. To overcome these drawbacks, we propose a new technique, which is very simple in implementation with high level of efficiency. The key is an image which is very difficult to be predict and the time for computation is reduced because no need to generate the key. The differences between our technique and the existing one are (1) We used the same methodology of chaos-based image encryption discussed in[5,7], with the change of the order of the stages to be performed in the image encryption/decryption, we run diffusion process and then confusion, this is because we use. (2) Number of iterations is one, as seen in figure 2 and can be compared with figure 1, where the encryption is performed in each pixel’s RGB component rather than the pixel’s value. (3) Our proposed technique is very simple in implementation. (4)The key is an image or matrix of random values, rather than generating key and add more complexity to the system. (5) the large key space is also one of the advantage of the proposed algorithm, since the key is an image which is very difficult to be predict, and the time for computation is reduced because no need to generate the key. (6) The technique can be extended to encrypt the video steams since the images in one frame are in the same size and one image-key is enough rather than generate key for each image in the frame. The rest of this paper is organized as follows. Section 2 presents the proposed algorithm. Section 3 describes the specification of the proposed algorithm. Section 4 describes the experimental result and Mean Square Error (MSE) results in varying some parameters of the algorithm, security analysis are given in Section 5. Finally, Section 6 concludes the paper.
2. Encryption Algorithm
- The proposed image encryption algorithm is based on chaos-based image encryption scheme; it uses as a key another encrypted image or any matrix of random values larger or of the same size of the plain-image. The operations needed in encryption and decryption processes are reduced, with high level of security and less computational time. figure 2 shows the block diagram of the proposed chaotic encryption algorithm, In algorithm 1, we explained the pseudocode of the proposed schemeAlgorithm 1: proposed chaos-based encryption scheme.Input: (1) Plain image P with M × N size.(2) Key image with M × N size. Output: encrypted image with M × N size.Begin1. Get the plain image (P) with M × N size. 2. Get the secret key image (K) with M × N size.3. For each pixel in P get RGB components (Pr,Pg,Pb). 4. For each pixel in K get RGB components (Kr,Kg,Kb).5. for each corresponding RGB components in P & K apply diffusion process defined as F(P(r,g,b) , K (r,g,b)) = C(r,g,b).6. Concatenate RGB layers in C with binary representation for each (8 bit in each layer) in the order RGB.7. Apply confusion processes (permutation with a selected 1D array of size 24 element.).8. Get the permuted combination and divide it into three parts which will be the three RGB layers of C. 9. Repeat step 3-8 to all pixels in P and the corresponding pixels in K to get pixels in C. End.The encryption steps are as follows:Step 1: Input to the algorithm the plan Image P with M × N size with key image K with M × N (same size).Step 2: For each pixel of P get RGB components and for each pixel of K get RGB components.Step 3: For each corresponding RGB components in P and K apply any logistic map to get new RGB components.Step 4: Concatenate the new RGB component to be 24 bit. Step 5: Perform the permutation process of the 24 bit with a selected 1D array of size 24 elements.Step 6: Form the new permuted RGB component construct gray value for the new pixel.Step 7: Perform steps 1 to 6 for all pixels in P.
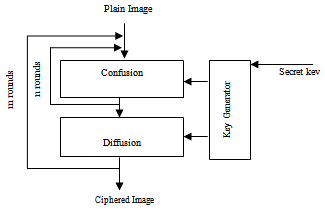 | Figure 1. Typical architecture of chaos-based image encryption scheme |
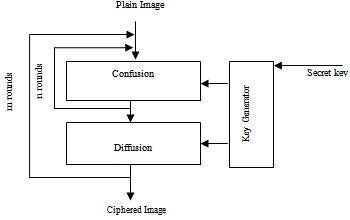 | Figure 2. Typical architecture of the proposed image cryptosystems |
3. Scheme Specification
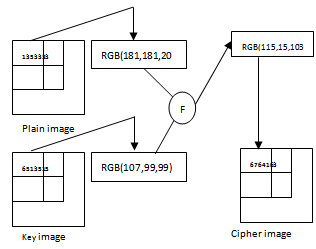 | Figure 3. Example of the proposed image encryption scheme |
4. Experimental Analysis
- Several images have been encrypted by using the proposed chaotic image encryption scheme. To measure the error in the plain-image and the encrypted -image, we use MSE error metrics[16]. The mathematical formula for MSE is as follows:-
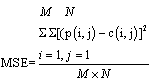 | (1) |
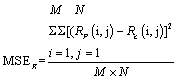 | (2) |
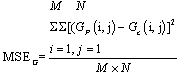 | (3) |
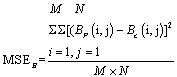 | (4) |
 | Figure 4. Image encryption experimental result 1: (a) Plain- image, (b) Key image, (c) Encrypted image |
5. Security Analysis
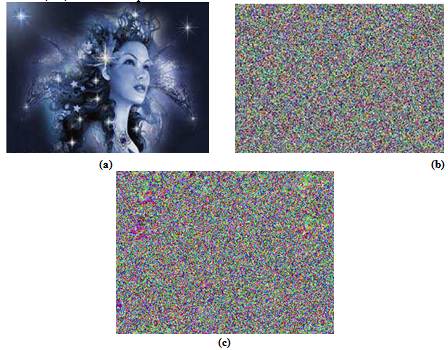
- The image encryption scheme presented in this paper is based on chaos-based image encryption scheme suggested by Fridrich[8]. Good encryption procedure should be robust against all kinds of known attacks[6]. The encryption procedure should be sensitive to the secret key and using different keys should not recover the plain-image. In our algorithm using different key will add more noises to the encrypted image instead of getting the plain-image as shown figure 5 experimental result 3. In our proposed algorithm, the key is a selected image which is larger or of the same size of the plain-image. using this key in encryption /decryption processes will overcome the drawbacks of the limited key space in[10] and satisfy high level of security. This is because it is very difficult to predict matrix of values, whereas using initial values for key generation might be feasible for brute force attack. Comparing the proposed technique with the latest existing technique proposed by M. Francois et al[17], in terms of security and complexity we found that our technique satisfied high level of security. In figure 6 we can see the Fairy’s image after encrypted by M. Francois's algorithm and the same image after encrypted by our algorithm. It can be seen that we have satisfied high level of security as our encrypted image looks like the one in[17]. In addition to that our algorithm is simple in implementation as number of operations is less than the number of operations in Francois et al[17]. Our algorithm is more secure as the key space is very large and it's difficult to be predicted.
5.1. Distribution of Pixels
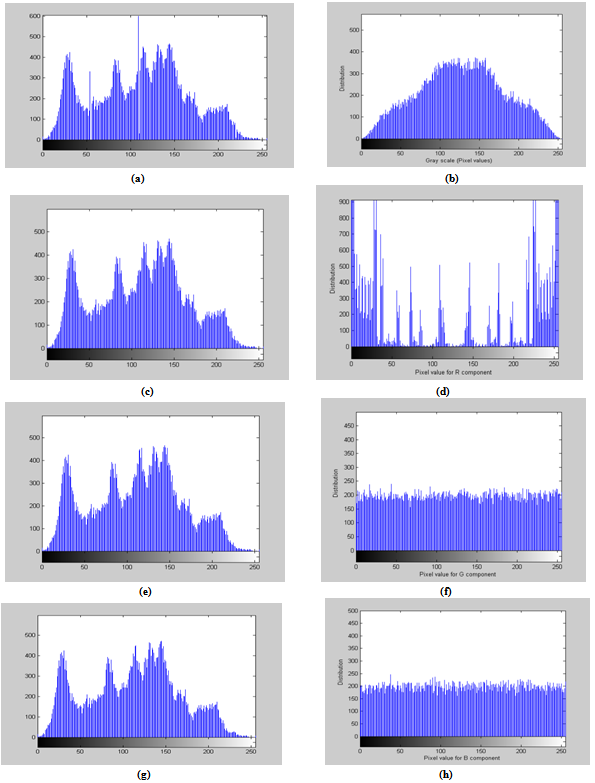
- The proposed image encryption algorithm experimentally tested on "Lena" image 225×227, and because our algorithm works on RGB images which are M×N×3, where the image can be considered as 3 dimensional image, so we need to get from M×N×3 image 3 different 2 dimensional images of size M×N for R, G, and B components of the image, because histogram can only applies on 2 dimensional image. We use this functions rgb2gray in matlab to convert RGB image into grayscale images. figure 8(a) shows the histogram of Lena image after converted form RGB image into grayscale image and the histogram of the encrypted image after converted form RGB into grayscale, but for more accurate results we need to get the histogram of R component of Lena image, and the histogram of R component of Lena encrypted image as shown in figure 8(c) and figure 8(d), the same we do on G and B component of Lena image and Lena encrypted image as shown in figure 8(e), figure 8(f), figure 8(g), and figure 8(h). As a result of this, we can see in figure 8 the pixels distributions of the original image and the pixels distributions of the encrypted image. Encryption process returns noisy images. The histogram of encrypted images in figure 8(d), figure 8(f), and figure 8(h) are very close to uniform distribution which are different from that of the corresponding original images in figure 8(c), figure 8(e), and figure 8(g). These aspects indicate high level of security against the known-plaintext attack[14].
 | Figure 7. Image encryption experimental result 4 using Lena Image: (a) Plain- image, (b) Key image, (c) Encrypted image, (d) The decrypted image |
6. Conclusions
- In this paper, we introduced a new image encryption algorithm based on chaos- encryption scheme. The encryption process is applied on RGB components of the image's pixel instead of the pixels itself. The encryption process uses another image as a key, this key-image should be larger or of the same size of the plain-image. In encryption process the corresponding RGB components in plain-image and key-image go through diffusion process and after that the ciphered image's RGB components are permuted on 1 dimensional array. To overcome the limitation of key space in[13] and the improved NCA algorithm in[10], we proposed our key to be an image or a matrix larger than or of the same size of the plain image. Using the key in this way, we reduced the number of operations for key generation as well as the key is secret to make brute-force attacks infeasible. Several Experiments were carried out with numerical analysis, to demonstrate the high level of security in the proposed image encryption scheme. The prototype system of the proposed algorithm can be used in any application of image transmission over unsecured channel. In the future work we intend to make our system flexible in key selection, so the system can generate the key as a matrix of random values larger or of the same size as the images we intend to encrypt.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML