1. Introduction

Probabilistic techniques in computer programs are becoming more and more widely used; examples are in random algorithms to increase efficiency, in concurrent systems for symmetry breaking, and in hybrid systems when the low-level hardware might be represented by probabilistic programs that model quantitative unreliability[1]. Therefore, there has been a renewed interest in methods for formal specification, verification, and development of probabilistic programs.

Methods for modelling probabilistic programs go back to the early work in[5] introducing probabilistic predicate transformers as a framework for reasoning about imperative probabilistic programs. From that time on, a wide variety of logics have been developed as possible bases for verifying probabilistic systems. A survey of this work can be found in[2].

In[1,3], Morgan et al. introduced probabilistic nondeterminism into Dijkstra’s GCL (Guarded Command Language) and thus provided a means with which probabilistic programs can be rigorously developed and verified. Although the semantics has been designed to work at the level of program code, it has an in-built notion of program refinement which encourages a prover to move between various levels of abstraction. In addition Morgan[16] extends Abrial’s GSL (Generalised Substitution Language) with a new probabilistic choice operator to create pGSL (probabilistic Generalised Substitution Language), a simple extension which can handle probability.

In[17], Hoang has developed a probabilistic B-Method (pB), which is an extension of B based on pGSL and includes developing a new syntax and semantics of a probabilistic Abstract Machine Notation (pAMN); an extension of AMN accommodating probability. Unlike publications of Morgan et al. and Hoang handling probabilistic choice in imperative settings, there are several studies considering probabilistic choice in functional languages; for example, see[10-12].

A statistical approach for probabilistic model checking has been presented in[19]. In[20], Kwiatkowska et al. give a short overview of probabilistic model checking techniques and then mention some of the limitations of these techniques. Finally they describe some of the advances that are being made to overcome these limitations. In[18] the existence of efficient approximation methods has been studied to verify quantitative specifications of probabilistic systems.

As far as we know, much of the work in the literature such as[18-22] has focused on the verification of probabilistic programs while besides a considerable trend in verifying probabilistic programs, there is a big interest in the formal specification and development of such programs. On the other hand, there is not any considerable work in the literature handling probability in the Z notation as a well known model based specification language.

In[4], we introduced a constructive framework allowing us to write probabilistic specifications formally and then drive functional probabilistic programs from correctness proofs of these specifications. In the proposed framework, we use a Z-based formalism to write specifications of probabilistic programs. Then, we translate the resulting probabilistic specifications into their counterparts in Z itself. Of course, to interpret the obtained specifications in Z, we use an existing, constructive set theory, called CZ set theory[8], instead of the classical set theory Z.

We choose CZ since it has an interpretation[8] in Martin-Löf ’s theory of types[15]; this enables us to translate our Z-style specification of a probabilistic program into its counterpart in Martin-Löf’s theory of types and then drive a functional probabilistic program from a correctness proof of the resulting type theoretical specification.

The proposed Z-based formalism benefits from a new notion of operation schemas, called probabilistic schema, intended to specify probabilistic operations. Also, since the schema calculus operations of Z do not work on probabilistic schemas anymore, it includes a new set of operators for the schema calculus operations negation, conjunction, disjunction, existential quantifier, universal quantifier, and sequential composition which properly work on probabilistic schemas as well as ordinary operation schemas.

The main contribution of the current paper is to show the resulting formalism can be used to specify any discrete-time and continues-time Markov chains which themselves are widely used to model stochastic processes with the Markov property and discrete state space[7]. We can mention the following benefits for the current work:

1. Notations such as Markov chains are suitable for modelling stochastic aspects of probabilistic systems while these systems are planned to implement various functional requirements (besides stochastic or probabilistic requirements) which can be specified formally using well known model based languages like Z. In this way, our formalism that is obtained from enriching Z specifications with probabilistic notions is appropriate for modelling both probabilistic and functional requirements simultaneously.

2. Our formalism inherits the benefits of Z as well:

√ It is based on the two well known underlying theories, i.e., the first order predicate logic and set theory. These two altogether makes learning and applying our formalism too easy.

√ Probabilistic schemas and the new set of schema calculus operations can be used to organize large specifications and increase the reusability of specifications.

√ Appropriate level of abstraction can be chosen when specifying various probabilistic specifications.

3. Since we provide an interpretation of our formalism in the Z notation itself, we can still use Z tools, such as Z-eves to check the type and consistency of the written specifications formally.

4. For the same reason as what was stated in the above case, we can still use various methods and tools which are targeted for formal validation, verification and program development based on the Z specification language.

The paper is organized in the following way. In section 2, we review our formalism by defining the notion of probabilistic schemas and showing how they can be used to model probabilistic operations. In section 3, we introduce a new set of schema calculus operations into the resulting Z-based formalism. In section 4, we show how one can apply the resulting formalism to specify Markov chains. The last section concludes the paper.

2. Specifying Probabilistic Operations

In this section, we review our Z-based formalism to specify probabilistic programs formally. To achieve this goal, we first define the notion of probabilistic schema by which one can simply model probabilistic operations.

Definition 2.1. The general form of probabilistic schemas is as follows:

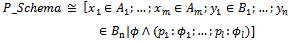where x_i (i: 1..m) are input or before state variables, and y_j (j: 1..n) are output or after state variables. Some part of the schema predicate, shown as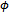, specifies those functions of the operation that are non-probabilistic; it specially includes the preconditions of the operation being specified. The remainder of the predicate is separated into l predicates 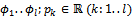are (constant) probabilities and by the notation 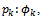we want to say that predicate 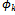holds with probability p_k. In other words, the relationship between the variables of P_Schema is stated by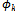with probability p_k. For a given probabilistic schema, we assume that p₁+...+p_l = 1 and for each k: 1..l, p_k ≥ 0. Notice that in the predicate part of P_Schema, l may be equal to 0, i.e., ordinary operation schemas are considered as special cases of probabilistic schemas.

In the next example, we use the notion of probabilistic schema to specify a simple probabilistic operation.

Example 2.2. Suppose that the state of the weather tomorrow only depends on the weather status today and not on past weather conditions. For example, suppose that if today is rainy in a specific area, tomorrow is rainy too with probability 0.5, dry with probability 0.4, and finally snowy with probability 0.1. By the following probabilistic schema, we specify the weather forecast for tomorrow provided that today is rainy. In this schema, x? and y! are the weather statuses for today and tomorrow, respectively. Also, suppose that we use values 1, 2 and 3 to specify dry, rainy and snowy statuses, respectively.

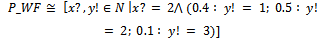The next definition introduces a function[]^P that maps probabilistic schemas into ordinary operation schemas of Z.

Definition 2.3. Recall P_Schema, given in definition 2.1 as the general form of probabilistic schemas. If for all real numbers p₁, ..., p_l, the maximum number of digits to the right of the decimal point is d, then we have:if P_Schema is an ordinary operation schema (i.e., when l = 0), then[P_Schema]^P = P_Schema;

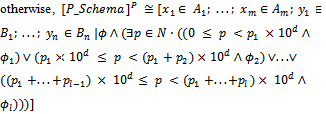[]^P behaves as an identity function when applied to an ordinary operation schema, i.e., when l = 0; otherwise, an auxiliary variable p ∈ N is introduced into the predicate part helping us to implement the probabilistic choice between l predicates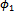,...,.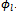 The variable p ranges nondeterministically from 0 to 10^d−1, and the length of each allowable interval of its values determines how many times (of 10^d times) a predicate 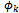(k : 1..l) holds (or in fact describes the relationship between the schema variables). More precisely, in p_k*10^d cases per 10^d times, the predicate 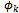(k : 1..l) determines the behaviour of the final program. In the next example, we apply the above defined interpretation to the probabilistic schema P_WF, given in example 2.2

Example 2.4. We use function[]^P to transform P_WF into an ordinary operation schema of Z as follows:

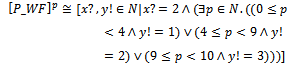By the above schema, p nondeterministically takes one of 10 values 0, 1, ..., 9. For four (i.e., in 4 cases per 10) possible values of p (i.e., 0, 1, 2, and 3), it has been specified that the weather is dry tomorrow. For other five (i.e., in 5 cases per 10) possible values of p (i.e., 4, 5, 6, 7, and 8), it has been described that the weather is rainy tomorrow. Finally, for the remaining (i.e., in 1 case per 10) possible value of p (i.e., 9), it has been indicated that the weather is snowy tomorrow. Thus, it seems that if one makes a uniform choice to select one of the values 0, 1, ..., 9 for p, s/he will be provided with a correct implementation of P_WF.

In[4], we showed the given interpretation of probabilistic schemas via Definition 2.3 is not enough for the purpose of constructive program development. Thus, we change the current interpretation such that it explicitly models all possible values of variable p and also all possible values of the after state and output variables of P_Schema, allowed according to the predicate part of this schema.

In this way, a sound, formal program development method is forced to construct a program that involves all possible values of p and also all possible values of the after state and output variables; such a program will be able to implement the probabilistic behaviour, initially specified by the probabilistic choice between l predicates ϕ₁,..., ϕ_l. The next definition introduces a new function[]^NP that interprets probabilistic schemas according to the new idea.

Definition 2.5. Recall P_Schema, given in definition 2.1 as the general form of probabilistic schemas. If for all real numbers p₁, ..., p_l, the maximum number of digits to the right of the decimal point is d, we have:

if P_Schema is an ordinary operation schema,[P_Schema]^NP = P_ Schema; otherwise,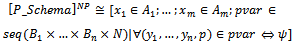

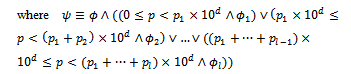Like[]^P, function[]^NP behaves as an identity function when applied to an ordinary operation schema; otherwise, it promotes the combination of the after state and output variables and an auxiliary variable p ∈ N to a sequence pvar of all possible combinations of these variables that satisfy the predicates of the schema. We have combined all of the above mentioned variables using the Cartesian Product of their types in order to preserve the relationship between them after the interpretation. The next theorem shows the recent interpretation of probabilistic schemas constructively leads to programs which can implement the probabilistic behaviour initially specified by probabilistic schemas.

Theorem 2.6. Assume that for every predicate 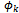(k : 1..l) existing in the predicate part of P_Schema, each combination of values of before state and input variables with one and only one combination of values of after state and output variables satisfies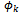. A program extracted from the correctness proof of the type theoretical counterpart of[P_Schema]^NP can implement the probabilistic behaviour specified by P_Schema.

Proof. Based on the predicate part of[P_Schema]^NP, a program satisfies^[P_Schema]^NP iff when applied to a combination of input values, it produces a sequence consisting of all allowable values of y₁, ..., y_n, p and not anything else. Therefore, any formal program development method that is sound (such as the constructive method of extracting programs from correctness proofs of type theoretical counterparts of Z specifications; see the soundness proof in[8]) absolutely extracts a program from[P_Schema]^NP that for each combination of input values, produces a sequence consisting of all possible values of y₁, ..., y_n, p and not anything else. On the other hand, by the assumption of the theorem, the resulting sequence includes 10^d elements from which 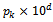(k : 1..l) elements implement the behaviour specified by ϕ_k. Thus, if we make a uniform choice over the elements of this sequence, we will be provided with a correct implementation of the probabilistic behaviour, initially specified by P_Schema.

In the next example, we apply the function[]^NP to the probabilistic schema P_WF, given in example 2.2.

Example 2.7. We use the function[]^NP to translate the probabilistic schema P_WF, given in example 2.2, into an ordinary operation schema of Z:

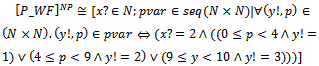We have so far proposed to use probabilistic schemas in order to specify probabilistic operations in our Z-based notation. A distinctive feature of Z is its schema calculus operations. In the next section, we show these operations do not work in the presence of probabilistic schemas anymore. We thus introduce a new set of schema calculus operations into the new formalism that can be applied to probabilistic schemas as well as ordinary operation schemas.

3. A Calculus for Probabilistic Schemas

We first investigate whether we can use the operations of the Z schema calculus to manipulate probabilistic schemas. It seems that a simple way to do this is to transform probabilistic schemas into ordinary ones (using the function[]^NP) before applying the schema calculus operations of Z; in this way, we will have ordinary operation schemas that can be manipulated by the Z schema calculus operations in the conventional way. However, we show that this approach may result in unwanted specifications; it even may make the applications of operations to schemas undefined. For instance, consider the probabilistic schema P_WF, given in example 2.2. This schema specifies a partial operation[6] since the effect of the operation is undefined for some input values, i.e., when x? <> 2.

To describe a total operation, we give a new specification:

indicates an unknown weather state for tomorrow. Now, we can describe a total operation by applying a disjunction between two schemas P_P_WF and Exception above. Before doing this, however, we first translate P_P_WF into an ordinary operation schema as follows: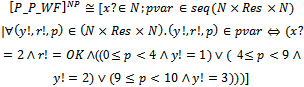

Since two schemas[P_P_WF]^NP and Exception are type compatible[6], we can apply the operator ⊦ to these schemas. However, in the resulting schema, there is no relationship between the variables y! and r! coming from Exception and the sequence pvar coming from[P_P_WF]^NP whereas all the elements of pvar involve instances of y! and r!. In this way, the resulting specification is unwanted, or in other words, does not correspond to what is intended by the initial specification. The problem originates from the fact that using[]^NP forces the output variables y! and r! existing in P_P_WF to be combined into a new variable, and the resulting variable to be promoted to a sequence.

Interpreting probabilistic schemas before applying the schema calculus operations may even yield undefined operations. For instance, suppose that we use ∃y! ∈ N · P_P_WF to hide y! in the resulting schema. If we use the function[]^NP to interpret P_P_WF before applying the existential quantifier, we miss y! since it is combined with some other schema variables and then promoted to a sequence; in this way, the quantification over y! becomes undefined.

Similar problems occur when we transform probabilistic schemas into ordinary ones before applying the other schema calculus operations, such as conjunction, universal quantifier, and sequential composition: by using[]^NP to interpret probabilistic schemas, the relationship between instances of a variable that exist in the declaration part of various schemas (or exist in the list of quantified variables and the declaration part of the quantified schema when using quantifiers) may be lost; hence, applying schema calculus operations to the resulting schemas may be undefined or result in unwanted specifications.

Unfortunately, another problem will occur if we try the reverse path, i.e., applying the schema calculus operations to probabilistic schemas before interpreting them by[]^NP. For instance, suppose that we apply the operator ⊦ to the schemas P_P_WF and Exception before interpreting P_P_WF:

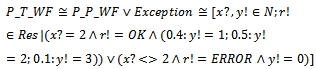P_T_WF does not correspond to the general form of probabilistic schemas (see definition 2.1). Therefore, we are not allowed to apply function[]^NP to interpret P_T_WF. It seems that we can solve this problem by manually transforming the resulting schema into the general form of probabilistic schemas or even changing the definition of[]^NP to cover schemas such as P_T_WF; however, having such a method in mind, in various situations we encounter various cases for each of which we must provide a special, manual way.

We have so far shown any of the mentioned paths (interpreting probabilistic schemas before applying the schema calculus operations or the reverse path) to employ the operations of the Z schema calculus in our formalism do not work when we want to manipulate probabilistic schemas. Now, we present another approach in which the application of operations and the interpretation of probabilistic schemas occur in an interleaved manner. Suppose that[]^NP operates in a two-step process, or in other words,[]^NP is equivalent to the composition of two functions[]^NP1 and[]^NP2; the former approximately behaves like the function[]^P introduced by definition 2.3, but unlike[]^P,[]^NP1 introduces variable p into the declaration part of the schema. Here is the formal definition of[]^NP1:

Definition 3.1. Recall P Schema, given in definition 2.1 as the general form of probabilistic schemas. Also assume that for all real numbers p₁, ..., p_l, the maximum number of digits to the right of the decimal point is d. Thus we have:if P_Schema is an ordinary operation schema,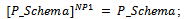

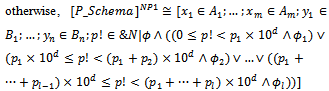In definition 3.1, we have used symbol & when declaring p! in order to be able to distinguish between probabilistic schemas and ordinary operation schemas when we want to apply[]^NP2 later. Based on the next definition,[]^NP2 takes a schema and promotes the combination of its output and after state variables to a sequence, provided that it includes an output variable declared by &.

Definition 3.2. Suppose that[]^NP2 applies to the following operation schema:

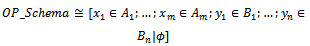where x_i (i : 1..m) are input or before state variables, and y_j (j : 1..n) are output or after state variables. Now, we have:if OP_Schema has no output variable declared by &, then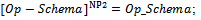

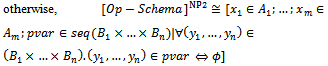It can be easily justified that[]^NP =[[]^NP1]^NP2. Now, to manipulate probabilistic schemas by the operations of the Z schema calculus, we propose to apply these operations between the applications of[]^NP1 and[]^NP2. An informal illustration of the correctness of this approach is as follows:[]^NP1 transforms a probabilistic schema into an ordinary one according to the probabilities involved in its predicate part; however,[]^NP1 does not promote the combination of the output and after state variables to a sequence. Therefore, we can apply the operations of the Z schema calculus to the resulting schema as usual; this does not yield unwanted specifications or undefined operations. At the final stage, we apply[]^NP2 to the resulting schema in order to enable the final program to implement the initially specified probabilistic behaviour.

To implement the above idea, we introduce a new set of schema calculus operations into our Z-based formalism that can be applied to probabilistic schemas appropriately. In the Z notation[6], there exist operators ¬, 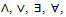and 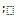for the schema calculus operations negation, conjunction, disjunction, existential quantifier, universal quantifier, and sequential composition, respectively. Here, we define a new set of operators consisting of 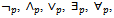and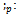

Definition 3.3. Let PS₁ and PS₂ be two probabilistic schemas. Now, we have: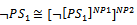

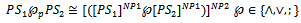
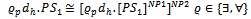where d_h is the declaration of quantified variables.

To show the usability of the new operations, we apply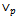to P_P_WF and Exception. By this example, we also show that in the case of disjunction between a probabilistic schema and an ordinary one, we must apply a slight change to the ordinary schema after using[]^NP1 and before using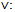

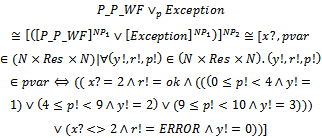The above resulting schema specifies a total operation. When x? = 2, this operation produces a sequence consisting of all allowable values of y! and p! and also reports OK. When x? <> 2, the operation assigns 0 to y! and reports ERROR; however, the possible values of p! has not been determined for this case, and p! can take any natural number; it violates producing a finite sequence for pvar.

To solve this problem, it is enough to introduce p! into the declaration part of Exception and add a conjunct such as p! = 0, limiting the possible values of p!, into the predicate part of Exception before using Vbetween P_P_WF and Exception. Notice that this modification is not required when we use conjunction or sequential composition operators between a probabilistic schema and an ordinary one since in these cases, we apply a conjunction between the predicate parts of two schemas; this scenario automatically limits the possible values of p!.

4. Specification of Markov-Chains

In this section, we show the resulting formalism can be used to specify any Markov chain. Markov chains are widely used to model stochastic processes with the Markov property (the next state of the system depends only on the current state) and discrete (finite or countable) state space[7]. Since usually a Markov chain would be defined for a discrete set of times, we first concentrate on discrete-time Markov chains.

Suppose that we are going to specify an arbitrary discrete-time Markov chain with n states S₁, ..., S_n (n ≥ 1). Also, suppose that for each S_i and S_j (1≤ i, j ≤ n), p_ij denotes the fixed probability that the system process will next be in state S_j, provided that it is in state S_i now. The state schema of the system and its initialization schema are as follows:

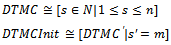where s and m indicate the current and initial states of the system, respectively.

Now, for each system state S_i (1 ≤ i ≤ n), we consider a probabilistic schema to model transitions from S_i to all system states (including S_i itself) as follows:

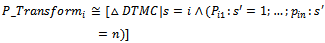Finally, having the above defined probabilistic schemas, the following specification describes the stochastic process formally:

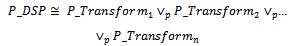Now, we are going to specify an arbitrary CTMC (Continuous Time Markov Chain) with n states, i.e., a stochastic process that moves from a state to another state similar to what we see in a Discrete Time Markov chain (DTMC); however, the amount of time which this process spends in each state, before proceeding to the next state, is exponentially distributed[9].

In practice, the transition probability function from state i to state j, shown as P_ij(t), is often not easy to be determined explicitly, so a CTMC is usually described by transition rates[9].

Whenever a CTMC enters a state i, it spends an amount of time, called the dwell time (or holding time) in that state. The holding time in state i is exponentially distributed with mean 1/q_i, where q_i represents the rate at which the process leaves state i. At the expiration of the holding time, the process makes a transition to another state j with probability p_ij, where:

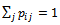We have a more notion: q_ij represents the transition rate from state i to state j. In other words, this is the mean number of transitions from i to j per unit time. In this way, we have q_ij = q_i*p_ij, and the following properties hold:

(1) q_ij determines the distribution of a CTMC completely as 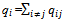and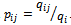

(2) By definition, a CTMC always goes to another state during a transition, thus, q_ij and p_ij are only defined for 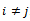We may set q_ii = p_ii = 0.

(3) In working with a CTMC, it is useful to think that from each state i, transitions to other states occur at independent exponential rates q_ij, that is, the transition times to other states are independent exponential random variables of means 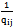(qij = 0 means no transition from i to j is possible).

Now having transition rates in place, the resulting formalism in sections 2 and 3 can be used again to specify any CTMC. The state schema of the system and its initialization schema are as follows:

[rate]

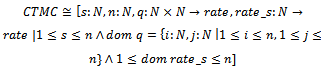where s shows the current state of the CTMC, n is the number of states, q is a function that shows transition rates for any two different states, and rate_s is a function that shows 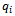for each state i.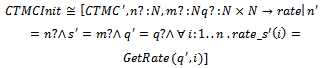

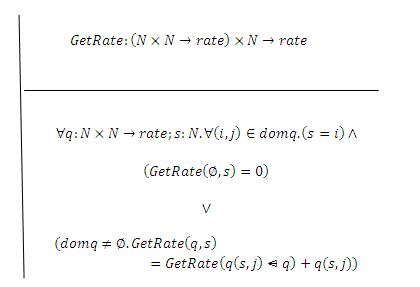Figure 1. Axiomatic definition of GetRate

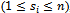Now, for each system state s, we consider a probabilistic schema to model transitions from to all system states as follows: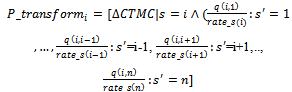

Since there is no transition from a state to itself, 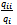is not considered in the constraint part of 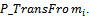Now, the total specification of the system is as follows:

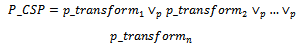Example 4.1. A computer system has three states: Idle, working, and failed; when it is idle, jobs arrive according to an exponential distribution with rate 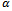and are completed according to an exponential distribution with rate. When the computer is working, it is failed according to an exponential distribution with rate w, and when it is idle, it is failed according to an exponential distribution with rate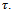.Finally, when the computer is in a failed state, it goes to the working state according to an exponential distribution with rate u.

We use values 1, 2 and 3 to specify idle, working and failed states, respectively, as shown in Figure 2:

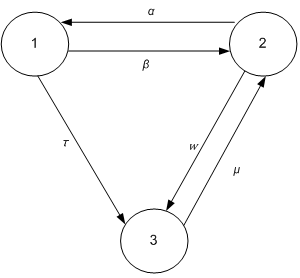Figure 2. Continues time Markov chain for a computer system

5. Conclusions and Future Work

In this paper, we have presented a Z-based formalism by which one can specify probabilistic programs formally. To demonstrate the applicability of this formalism, we have shown that any probabilistic system that can be modelled with Markov chains can be formally specified using this formalism. However, the resulting formalism can only specify Markov chains in the origin time. In other words, this formalism specifies stationary Markov chains and cannot be used for dynamic specification of Markov chains. So, future work would offer a formalism based on Z that has the capability of specifying dynamic Markov chains and probabilistic systems that change during time.

In addition, the current formalism suffers from a main drawback: as was stated in[4], the interpretation function[]^NP can be only applied to those probabilistic schemas

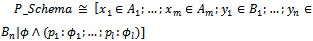that obey the following law: for every predicate ϕ_k (k: 1..l), each combination of values of before state and input variables with one and only one combination of values of after state and output variables satisfies ϕ_k.

To compare our work with other approaches in the literature which apply formal methods to probabilistic systems, it is worth mentioning that, as we have stated in section 1, most of the contributions in the literature have focused on the verification of probabilistic programs. As one related work, we can point to[13] in which a rewrite based specification language, called PMAUDE, has been proposed for specifying probabilistic concurrent and real-time systems. Specifications in PMAUDE are based on a probabilistic rewrite theory which has both a rigorous formal basis and the characteristics of a high-level programming language. In other words, this theory allows us to express both specifications and programs within the same formalism.

Although our specification language in this paper is based on a different theory in comparison to that of[13] (i.e., set theory in comparison to rewrite theory), we are going to utilize one advantage of[13] in our future work; this advantage is that PMAUDE allows specifications to be easily written in a way that they have no un-quantified nondeterminism. More precisely, all occurrences of nondeterminism are replaced by quantified nondeterminism such as probabilistic choices and stochastic real-time; hence, this work does not have the problem of ours when both nondeterminism and probability exist in the specification simultaneously.

As another related work, we can point to[14] in which a formalism that is based on the notion of state-transition is proposed to specify probabilistic processes. In this work, Jonsson and Larsen define a refinement relation between probabilistic specifications as inclusion between the sets of processes that satisfy the respective specifications. One of the most advantages of[14] is the ability to consider variable probabilities for each transition. More precisely, each transition is labelled by an appropriate interval of probabilities. Although we use a different theory (set theory instead of state-transition) as the basis of our specification language, we are going to employ the idea of[14] to enrich our framework to support variable probabilities.