1. Introduction

The emergency population has been growing remarkably owing to either the rapid rise of the general population or the changing living style around the world, which gives the emergency department (ED) an important role in the hospital[1]. It is reported that every activity in the emergency care setting must fall under the quality assurance umbrella, ensuring that quality of service is maintained at a high leve1[2].

The increased demand on the ED stretches its abilities to provide efficient, consistent, and cost-effective care while at the same time attempting to keep patients satisfied and avoid malpractice risk. Given that many EDs commonly experience crowding today, emergency physicians, management, and staff must seek ways to meet these challenges or face losing their patient base, providing unsafe or substandard care, losing staff, or risking financial integrity.

The evaluation of patient flow through the ED is one of the important quality assurance activities. Identifying patient flow bottlenecks also aids in decision-making regarding ED organization, including staffing, triage, space use, and overall resource allocation.

Since the early 1970s a growing use ED services by the public has focused concern on how departments manage this increased patient flow.

Historically, ambulance diversion was created to offer temporary relief to ED. Ambulance services must send a vehicle to the site of a medical emergency as fast as possible. Since they deal with life and death situations, They have drawn extensive attention from operations research[3].

In the ED of Sfax hospital the patients’ dangerous case could be transported by ambulances. This way the purpose of this study was to demonstrate the application of Dial-A-Ride Problem (DARP). This method involves the dispatching of a fleet of vehicles to satisfy demands from customers who contact a vehicle operating agency requesting to be carried from specified origins to other similarly specified destinations, as defined in[4].

The objective of this paper is to find some solutions in order to minimize the emergency patient’s transportation required related to the service cost.

Our contribution is twofold: our first original contribution brings in a variant of Routing Problems known as the Dial A Ride Problem (DARP), with a major contribution, which the paper presents in the Tunisian case study.

Second, a major contribution of the paper is the development of an efficient methodology based on the CPLEX solver which provides a high-quality solution.

This paper is organized in the following sections as follows. Section 2 introduces the context of study. Section 3 describes the literature review. The proposed model and definition problem are presented in Section 4. Section 5 presents the experimental results performed for the real and simulated scenario. Finally in Section 6 we conclude the paper.

2. Context of this Study

Habib Bourguiba hospital is presented as follows:

● Hospital-academic centre since 1985 ;

● Erected in public establishment of health since 1993.

The missions of the hospital are:

● To lavish current pathology cares and essentially cares of reference;

● To assure the formation convenient of basis and retraining of the medical and decorate-medical personnel

● To develop the activity of research in the medical domain and cares male nurses.

The hospital includes 18 Departments; most important it is the Emergency Department that represents the door of entrance of the hospital.

The geographical situation of the Sfax city to the centre of the country, point of link between the south and the north of the country, makes that the Emergency Department receives an important number of casualties of the public way. As second economic and industrial pole sheltering a lot of companies, the city knows an elevated number of work casualties.

The department includes:

● 2 rooms of care;

● 1 room of plaster;

● 2 post office;

● 1 room of general surgery ;

● 1 room of orthopedy;

● 1 room of visiting medical;

● the overage number of patients in day is ±300,

● The number of personnel is 13.

The ED of Habib Bourguiba Hospital includes 4 ambulances. When the switchboard operator receives a phone call from a patient or a complaint of an accident, a team composed of a doctor, nurse and a driver will move the ambulance to bring the patient and treat him in the department. Each ambulance can carry only a single patient.

For the arrival of the patient, we distinguish 2 possibilities: either he / she will come by himself or, in dangerous cases, he will be transported by the ambulance. At the arrival, the patient will pass by a triage process that will define the Emergency degree and then the process that will be taken by the patient. In fact there are two processes that can be taken by the patient, given the result of the triage process.

In both cases, the remaining process will be almost the same. In fact, the main difference concerns the administrative process. Thus, for a dangerous case, this process will be reported at the end of the patient process while for a non dangerous case, this process will be at the beginning of the whole process.

The remaining tasks of the process are the same as those of a normal consultation process. In fact, the patient will see a doctor who will determine the patient’s state and if necessary ask for supplementary analysis. Given the analysis results, the doctor will either care the patient by him self or ask for a specialist. In both cases, the patient could be hospitalized or go home.

Many researches have been treated about ambulance services; In[5] we analyse an ambulance service that takes emergency and regular calls. They conclude that, in order to respond to emergencies with promptitude, regular calls must be served only if a minimum number of vehicles remain idle. In paper[6] we study an ambulance system using the “hypercube” model, which consists of a multidimensional Markov chain of multiple queues, one at each base. The authors in[7] propose a method for calculating the ambulance busyness probabilities within the model. In[8] we use the hypercube to estimate the expected performance of an ambulance service in a Brazilian highway. Also in[9] we use it to evaluate how much to decentralize an urban ambulance service.

Queuing models are an abstraction of Markov chain models. In[10] we assess their empirical validity to assign patrols to New York City police stations. They conclude that queuing theory provides good approximations of the system behavior. In paper[11] we configure a fleet whose vehicles get calls while on the route. The objective is to minimize operating costs subject to several constraints, including a maximum waiting time for customers, modelled using queuing formulas.

The most well known application for the ambulance service problem arises in the door-to-door transportation services for patients. These patients are transported individually between specified origins and destinations. This problem application based on the concepts of the Pickup and Delivery Problems (PDPs). In these problems, a set of loads (goods, clients, patients etc.) with known locations (origins and destination) are assigned to a number of available vehicles[12]. Generally, the aim in PDPs is to maximize the service quality while minimizing the number of the used vehicles under the constraints of desired times of transportation and vehicle’s capacity. The two well-known examples in PDPs are the Dial-A-Ride Problem (DARP) and the Vehicle Routing Problem (VRP)[13-16].

3. Literature Review

Dial-A-Ride (DAR) is one of the public transit services which can provide shared-ride door-to door service with flexible routes and schedules. In a Dial-A-Ride Problem (DARP), passengers specify transportation requests with their origins, destinations, and desired pickup or delivery times. A set of routes and schedules must be determined to best accommodate the demand under a set of constraints. The two most common service quality constraints relate to maximum time deviation from desired time, i.e., the difference between the actual pickup/delivery time and the desired pickup/delivery time, and maximum ride time, i.e. the actual passenger in-vehicle time.

The DARP is a generalization of the Pickup and Delivery Problem (PDP) and the Vehicle Routing Problem (VRP), which are known to be NP-hard. The DARP is a PDP in which the loads to be transported represent people (in our case patients). Usually in the DARP maximum ride time constraints are considered and time windows are narrower than those in the PDP. The DARP is different from and somewhat more difficult than most other routing problems due to the precedence and maximum time constraints, the tight time window constraints and also because operator cost and user inconvenience must be weighted against each other when designing a solution instead of considering only operator cost. For a DARP overview, see[13]. Other related overviews include[17] for general routing and scheduling of vehicles and crews,[18] and[19] for vehicle routing and scheduling problems with time window constraints, and[20-22] for the general PDP. The following review focuses on the scientific literature specific to the static DARP. Due to the NP-hard nature of the DARP, its solution methods are almost exclusively heuristic except for very small single-vehicle problems. In[23],[24] we develop an exact dynamic programming algorithm for the single-vehicle static problem without and with time windows. Less than 10 customers are considered in his example. In the article[25] we solve the single-vehicle problem by formulating it as an integer problem and solving it exactly by dynamic programming. Instances with up to 40 users have been solved. Other heuristic approaches for the single-vehicle problem include the work by[24, 26].

The heuristics for the multi-vehicle DARP can be classified primarily into four general categories: insertion based cluster-first route-second, metaheuristics and improvement procedure. An insertion-based algorithm inserts one passenger request into the vehicle routes at a time, at a position that is feasible and results a minimum increase of a pre-specified objective function. The general insertion-based method includes work by[27-30] with regret insertion method. The basic idea of the insertion method was applied in other studies with special objectives[31-33].

Cluster-first route-second is a commonly used technique in various VRPs and has been attempted in the DARP. It is usually embedded with the mathematical programming technique for solving the clustering and/or routing phases. Authors in[26] apply Benders’ decomposition procedure to a mixed binary nonlinear formulation of the static single vehicle problem, which separates the routing and scheduling components allowing each to be attacked individually. We further develop a cluster first, route and schedule second and swap the third heuristic for the multi-vehicle problem.[34] solve the multiple-vehicle DARP by mini-clustering first, routing second. In[35] we improve the mini-clustering phase by using a mathematical optimization technique to form the mini-clusters and solving the problem by column generation. In[36] we use a set partitioning approach for the solution of the problem. In[37] we approach the problem by using simulated annealing for clustering and a modified space-time nearest neighbour heuristic for developing the routes for the clusters.

In the third category,[13] use a tabu search heuristic for the static DARP, which is extended by[38] for the dynamic version by using the parallel computing technique. We also develop a tabu thresholding procedure[39], which can improve the solution obtained by their insertion heuristic. We develop a simulated annealing based solution heuristic for the Dial-A-Ride Problem in[40]. The heuristic is computationally expensive (e.g. a 30 or 40 customer problem will require thousands of seconds). The improvement category includes the work in[41] who develop a local search method for the single-vehicle pickup and delivery problem with time windows based on a variable-depth search, and work by[42] who describe local search refining procedures which can be used to improve the solutions for large problems obtained by a parallel insertion heuristic.

Insertion heuristics have proved to be popular methods for solving a variety of vehicle routing and scheduling problems because they are fast, can produce fair solutions, are easy to implement, and can easily be extended to handle complicating constraints[43].

A comparative study by[19] indicates the insertion method is an effective heuristic for the vehicle routing problem with time windows, especially for heavily time-constrained problems.

The cluster-first route-second approach is difficult to apply to the DARP since the cluster phase needs special considerations due to the DARP pairing and time window constraints. Metaheuristics such as tabu search are computationally very expensive and their performance is directly related to running time and calibration of the algorithm parameters. Also, for a heavily constrained problem such as DARP, it is very difficult to maintain the feasibility in each local neighbour movement, or converge to a final feasible solution if infeasibility is allowed during local movements.

4. Problem Definition

A generalization of the well-known Travelling Salesman Problem is the standard multiple Travelling Salesman Problem (mTSP). The problem can be defined simply as the determination of a set of routes for m salesmen who all start from and return to a single home city (In this context the ED of Sfax hospital).

Consider a complete directed graph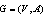, where Vis the set of n nodes (vertices), Ais the set of arcs and 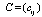is the cost (distance) matrix associated with each arc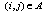. The cost matrix C can be symmetric, asymmetric or Euclidean. Let there be m salesmen located at the depot city 1. Then, the single depot mTSP consists of finding tours for m salesmen such that all start and end at the depot, each other node is located in exactly one tour, the number of nodes visited by a salesman lies within a predetermined interval, and the overall cost of visiting all nodes is minimized.

Let us define 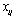as a binary variable equal to 1 if arc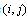is in the optimal solution and 0 otherwise. For any traveller, 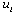is the number of nodes visited on that traveller’s path from the origin up to node i (i.e., the visit number of the ith node). Lis the maximum number of nodes a salesman may visit; thus,  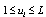; for all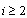. In addition, let Kbe the minimum number of nodes a salesman must visit, i.e., if 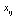= 1, then 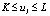must be satisfied.

In[44] we propose the following integer linear programming formulation for the mTSP defined above:

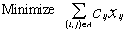(1)

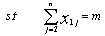(2)

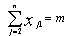(3)

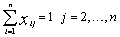(4)

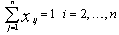(5)

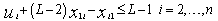(6)

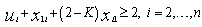(7)

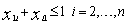(8)

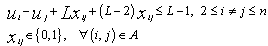(9)

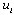In this formulation, constraints (2) and (3) ensure that exactly m salesmen leave from and return to the depot. Constraints (4) and (5) are the degree constraints. The inequalities given in (6) and (7) serve as upper and lower bound constraints on the number of nodes visited by each salesman, and initialize the value of to 1 if and only if iis the first node on the tour for any salesman. Inequality (8) forbids a vehicle from visiting only a single node. The inequalities given in (9) ensure that 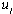= 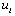+ 1 if and only if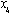= 1.

5. Experimental Results

This section provides an empirical study of the performance of the proposed methodology (CPLEX) to solve the assessing of an ambulance service for the patient transportation.

Computational experiments are performed on real and simulated case instances using CPLEX 10.0 on personal computer Intel® Core 2 Duo CPU 2.0 GHZ.

The calculations were carried out on a windows cluster. We used ILOG OPL 6.1 as modelling language and the mixed integer solver from CPLEX 10.1 (ILOG, 2007) commercial software for all the variants of the problem. Our algorithms are coded in C++ using Microsoft Visual Studio 6.0. CPU times are given in seconds.

We implemented this model with the commercial software "CPLEX" to find optimal solutions of the Dial-a-Ride problem and Emergency Transportation Problems. Unfortunately this software only works for a reasonable size instances and it does not return optimal solutions when the size is very large.

5.1. Simulation Scenario

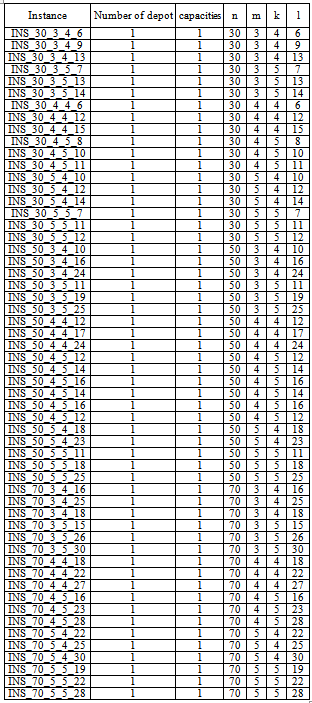
The simulation scenario consists of a number of nodes that are initially placed randomly and are constantly moving in a simulation circular area.

The table below presents our simulation scenario executed with the same parameters and interval presented in the paper of[44]. For this object, we have randomly generated (asymmetric) instances with three sizes of number of nodes (n=30, 50, 70) and using a value of maximum five number of vehicles (m=3, 4, 5). We have tested various values for the parameters K and L.

● For n=30, 50, 70; .

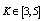● For n = 30 ;

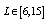● For n = 50 ;

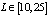● For n = 70 ;

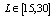The elements of the distance matrix have been randomly chosen from the interval[1, 10].

Table 1. Benchmark instances

Table 2. Problem input

Table.3. Real word problem

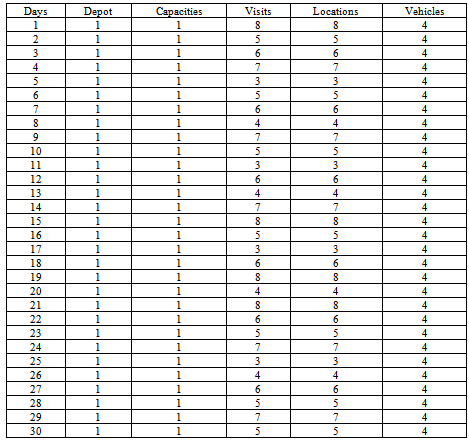
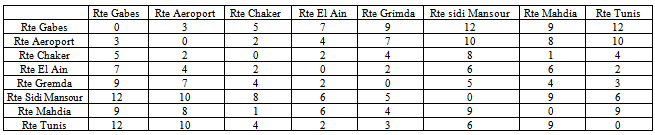
5.2. Real-world Instances

We have also applied the different solution algorithms to 15 real-world instances from the Habib Bourguiba hospital.

The model has been tested using 30 days of real data obtained from the ED of Sfax hospital. Table 2 and 3 illustrates the input statistics and the real word problems.

5.3. Evaluation method

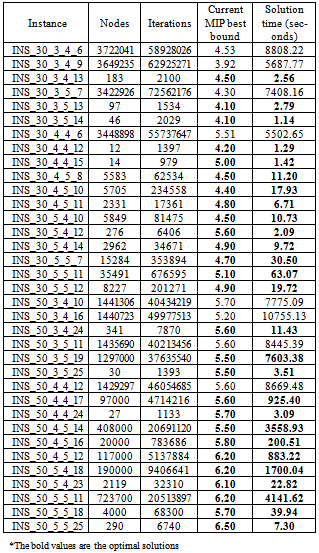
To test the effectiveness of our solution methodology by the CPLEX solver and for our simulation instance and real word instance we provide experimentation for all benchmarks problems. The number of instances generated from each problem is given in Table 1. Table 4 shows the results of all instances. As we have shown that twenty height out of thirty five test problems, the CPLEX solver find the exact solution.

Compared to results of operational methods produced by the emergency department of the hospital Habib Bourguiba Sfax, our solutions are considered better and more efficient and competent.

In fact, the empirical results provide work that the responsible of the transport of patients in the emergency department of the hospital Habib Bourguiba Sfax must rebuild their fleet of ambulances in traffic to reduce the total distance travelled.

The numerical results show that the proposed method is robust and efficient, especially for problems with moderate high size. The computation time provided by CPLEX is acceptable, although the number of variables was multiplied by a factor of 2 or 3 with respect to value for resources. This can be explained by the fact that the problem is more limited, and given that the number of possible solutions is reduced. It is becoming easier to find an optimal assignment of considered vehicle tours.

Table 4. Computational results

6. Conclusions

In this study an application of service ambulance in ED of Sfax hospital is presented. In this paper, based on experimentations conducted on instances of moderate size drawn from a real case study also an instances based on simulation scenario based on the data taken from the literature, we conclude that the methodology proposed by the solver CPLEX is able to solve the emergency transportation problem optimally in this case study.

Our approach is competitive compared with the results of the hand main used in the transportation of patients in the emergency department of the hospital Habib Bourguiba Sfax.

Future work may focus on developing a model of DARP problem using genetic algorithm.