1. Introduction

Particulate composite materials are widely used in industrial products and engineering structures due to their merits such as easy-to-manufacture, customized mechanical properties and great flexibility of design. Prediction of composite elasticity constants based on phase properties is a key task in the design of various composite materials. There are primarily three categories of methods available for the prediction of composite properties, i.e. mechanical testing [1-3], analytical micromechanics models [4,5] and finite element modeling of representative volume element (RVE) [6-9]. Mechanical testing is direct and reliable, but it is also time-consuming and expensive. Micromechanical models are the most efficient and convenient ones, because they offer analytical expressions. Nevertheless, they are usually based on special assumptions, for example dilute dispersion. Therefore, they have limited accuracy for composites that do not strictly satisfy the assumptions, e.g. composites that have large contrast of phase properties and high volume-fraction of inclusions [5]. Finite element modeling of RVE has the merits of both mechanical testing and micromechanical models, but avoids their drawbacks. Therefore, finite element modeling of RVE is widely applied in the study and design of composite materials [10-14].

There are basically two types of finite element modeling approaches available for elasticity prediction of composite materials, one is geometry based [10,15], the other is voxel based [16,17]. Take particulate composite as an example, in geometry-based finite element modeling (GB-FEM), a geometric model of the microstructure of RVE, which includes matrix and inclusions, is first constructed; Material properties are assigned to the matrix and the inclusions; A finite element mesh is then generated from the geometric model; Appropriate loading and constraint conditions are applied for the characterization of various elastic properties. Although theoretically geometry-based finite element modeling is an ideal tool for composite property prediction, there are a number of practical challenges. The first one is in the construction of a workable RVE geometric model [10,18]. Inclusions in actual composites are random distributed and have different geometric shapes and sizes. Inclusions (e.g. two spheres) that are infinitely close to each other may result in severely distorted and even degenerated geometric entities. This kind of geometric model is difficult to create even with relaxed geometric tolerances. Even with a valid RVE geometric model, there are still challenges in the generation of high-quality finite element meshes [19,20]. The existence of distorted and degenerated geometric entities may first fail the generation of a finite element mesh and then may result in severely distorted finite elements. Mesh quality significantly affects the accuracy of finite element solutions. To improve mesh quality, adaptive meshing has to be used [20], which is time-consuming but still cannot guarantee the quality.

Voxel-based finite element models (VB-FEM) constructed from quantitative computed tomography (CT) or micro-CT are often used in the study of bone mechanical properties [17,21-23]. The main difference between VB-FEM and GB-FEM is in the generation of finite element mesh. In contrast to GB-FEM, where a finite element mesh is generated from a geometric model, VB-FEM directly converts voxels in digital images into brick elements. Another advantage of VB-FEM is that material properties are reflected in voxel intensity or Hounsfield Unit (HU), which provides realistic information on the distribution of inhomogeneous bone density. There are two major concerns about VB-FEM. One is its computational efficiency. Since digital images usually consist of a large number of voxels, the resulting finite element meshes usually consist of a huge number of elements. The other concern is the non-smoothness of model boundaries, which may introduce stress concentration.

Despite of the above concerns, VB-FEM avoids the difficulties of GB-FEM in the creation of geometric model and in the generation of high-quality mesh. Voxel-based finite element meshes always have good quality. For the above reasons, we are motivated to compare the accuracy and efficiency of GB-FEM and VB-FEM in elasticity prediction of particulate composites, to study the possibility of using VB-FEM in elasticity prediction of particulate composites to avoid the difficulties of GB-FEM.

2. Materials and Methods

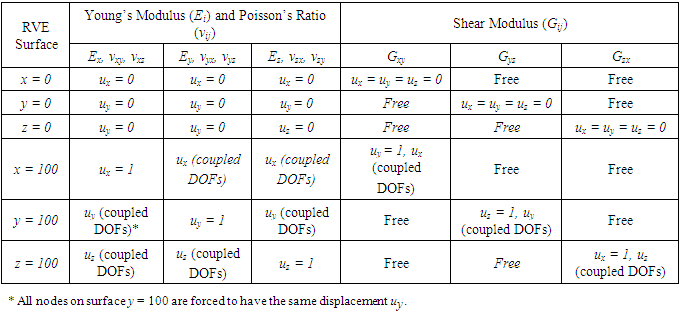
To compare their performance, GB-FEM and VB-FEM are constructed from the same composite RVE as illustrated in Figure 1. In GB-FEM, the matrix and the inclusions are meshed separately. A number of issues are introduced by this strategy, which has been discussed before. In contrast, for VB-FEM a uniform grid mesh is first generated for the whole domain occupied by the RVE. Then, the information of inclusion location and size in the RVE are used to identify the elements that belong to the matrix and the inclusions respectively. The resulting finite element mesh with distinguished Table 1 matrix and inclusions looks like a binary digital image, therefore, the terminology of voxel is used. As it will be shown later, the resolution of VB-FEM mesh, defined as the ratio between element size and the RVE size, affects the accuracy of VB-FEM. The rest steps of finite element analysis, including assignment of material properties and application of loading and constraint conditions, are the same as in GB-FEM. The objective of this comparison study is to find out whether or not GB-FEM and VB-FEM have good agreement upon their convergence, and what are their relative computational efficiency.

Table 1. RVE boundary conditions for characterization of composite elastic properties

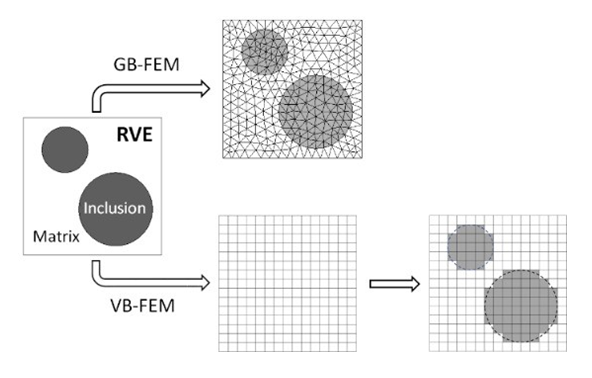Figure 1. Construction of GB-FEM and VB-FEM from the same composite RVE

RVE elastic properties, including Young’s modulus, Poisson’s ratio and shear modulus, are predicted by GB-FEM and VB-FEM using the same loading and constraint conditions. A cubic RVE with the setup of a coordinate system is shown in Figure 2. The side length of the RVE is L = 100 units, the unit can be at any length-scale from nanometer to meter, because in principle both GB-FEM and VB-FEM are applicable to problems of any length-scale.

Figure 2. Cubic RVE and coordinate system

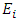The loading and constraint conditions listed in Table 1 are applied to the RVE for the prediction of Young’s modulus , Poisson’s ratio 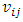and shear modulus 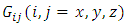. The applied constraint conditions are intended to mimic the behavior of the RVE in a larger material body and to avoid ‘artificial’ stress concentration. Take Young’s modulus 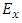as an example, the RVE surfaces at x = 0, y = 0 and z =0 are constrained in x, y and z direction, respectively; a uniform displacement is introduced on surface x = L; the surfaces y = L and z = L are forced to have uniform displacement from Poisson’s effect.

After the solution of the finite element equations, RVE Young’s modulus, Poisson’s ratio and shear modulus are determined by the homogenization theory based on volume-averaged stresses and strains [24-26], i.e.

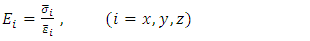(1)

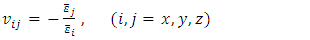(2)

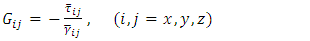(3)

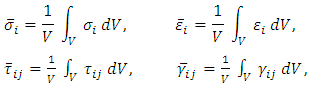(4)

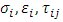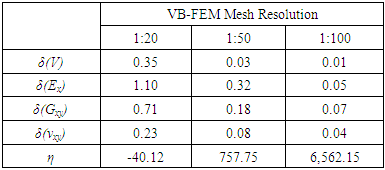
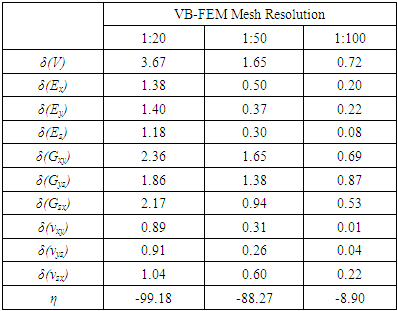
In the above equations, , and 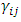are respectively the normal stress, normal strain, shear stress and shear strain determined by the finite element analysis; V is the volume of RVE.

Agreement between GB-FEM and VB-FEM is measured by the following normalized difference,

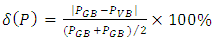(5)

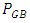Where P is a property of the RVE, for example, Young’s modulus, Poisson’s ratio, and shear modulus; is the elastic property predicted by GB-FEM upon convergence; 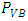is the property obtained by VB-FEM with a certain mesh resolution. A smaller δ value indicates a better agreement between GB-FEM and VB-FEM; If δ = 0, there would be no difference.

To compare computational efficiency of GB-FEM and VB-FEM, normalized number of nodes (η) is used, which is defined as

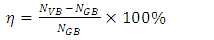(6)

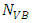Where and 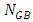are respectively the number of finite element nodes in VB-FEM and GB-FEM. If η > 0, more nodes are used in VB-FEM than in GB-FEM; otherwise less nodes are used.

3. Numerical Examples and Results

A polymer filled with small glass spheres [3] is selected for this comparison study. The polymer (matrix) has Young’s modulus 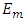= 2.68 GPa and Poisson’s ratio 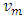= 0.394; The glass spheres (inclusions) have Young’s modulus 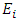= 70.0 Gpa and Poisson’s ratio 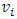= 0.23. Two types of RVE of the composite, as shown in Figure 3 and Figure 4, are constructed to compare GB-FEM and VB-FEM. RVE 1 in Figure 3 has large size and regularly distributed spheres, while RVE 2 in Figure 4 has small size and randomly distributed spheres.

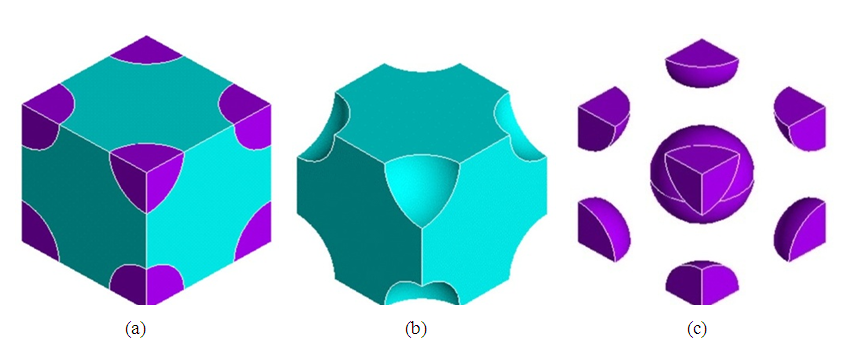Figure 3. RVE 1: regularly-distributed and large-size spheres. (a) composite; (b) matrix; (c) inclusions

Figure 4. RVE 2: randomly-distributed and large-size spheres. (a) composite; (b) matrix; (c) inclusions

All finite element results are produced using ANSYS Mechanical APDL (2020 R1, ANSYS, Inc.). In GB-FEM, 6-node tetrahedral element is used with mesh adaptation; In VB-FEM, 8-node brick element is used.

For RVE 1, sample GB-FEM and VB-FEM meshes are displayed respectively in Figure 5 and Figure 6. Variations of Young’s moduli predicted by GB-FEM and VB-FEM with the number of element nodes are shown in Figure 7.

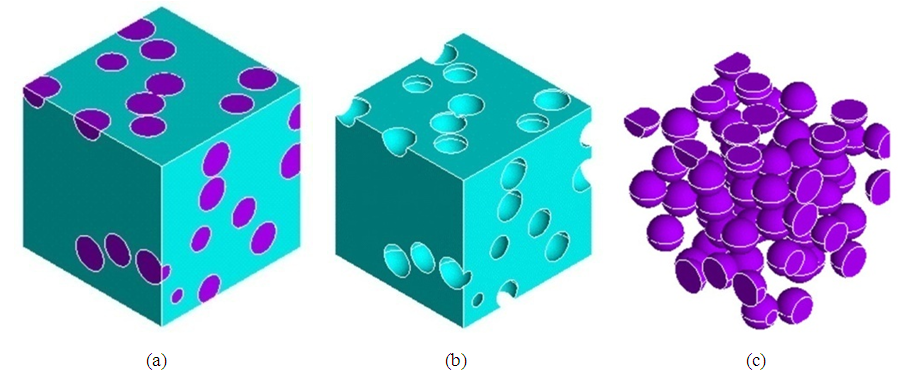
Figure 5. GB-FEM of RVE 1. (a) whole model; (b) matrix; (c) inclusions

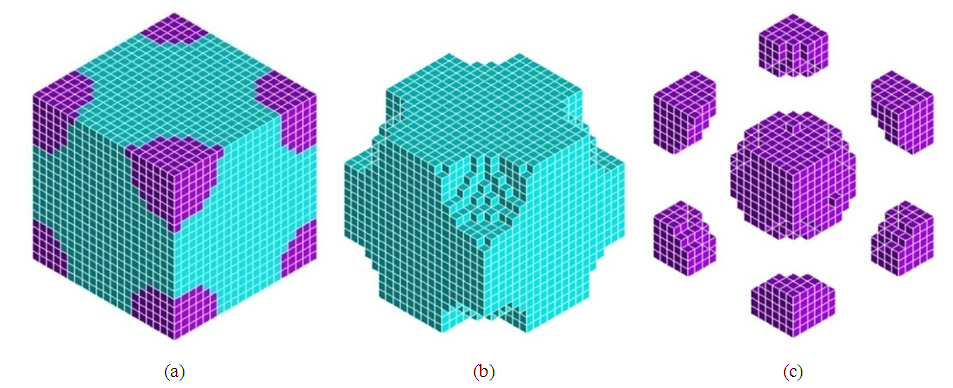Figure 6. VB-FEM of RVE 1. (a) whole model; (b) matrix; (c) inclusions

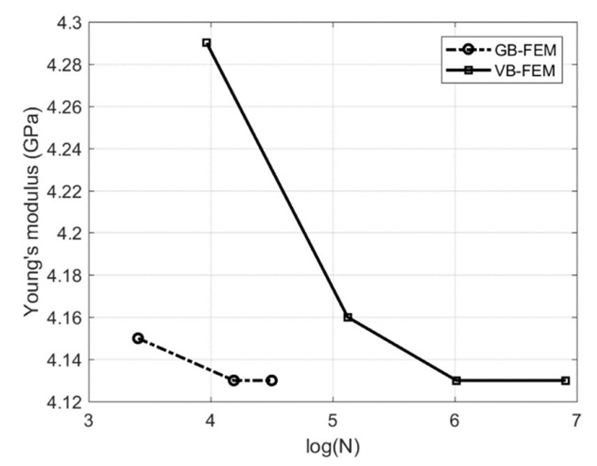Figure 7. Variation of RVE Young’s modulus with number of nodes (RVE 1)

Normalized differences between GB-FEM and VB-FEM are provided in Table 2, where the normalized differences (δ) are calculated based on Equation (5) and the normalized number of nodes is determined by Equation (6). It should be men-tioned that δ(V) in Table 2 (as well in Table 3) is calculated from the volumes of elements representing the spherical inclusions, there is a difference between the sum of the element volumes and that of the spheres.

Table 2. Normalized differences (%) between VB-FEM and converged GB-FEM (RVE 1)

Table 3. Normalized differences (%) between VB-FEM and converged GB-FEM (RVE 2)

For RVE 2, sample meshes are displayed in Figure 8 and Figure 9. Variations of Young’s moduli predicted by GB-FEM and VB-FEM with the number of element nodes are shown in Figure 10, the Young’s modulus in the figure is the average of Young’s moduli in the x, y and z axial direction shown in Figure 2. The normalized differences between GB-FEM and VB-FEM are provided in Table 3.

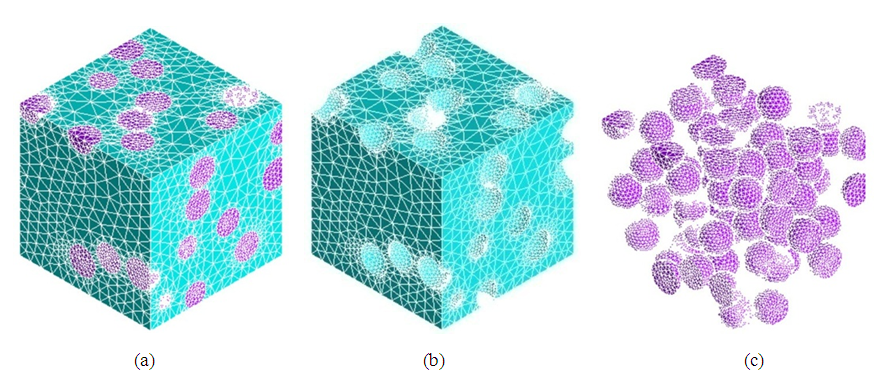Figure 8. GB-FEM of RVE 2. (a) whole model; (b) matrix; (c) inclusions

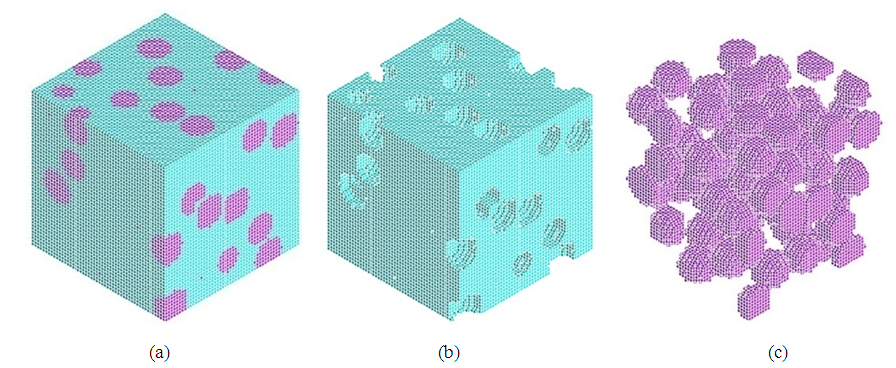Figure 9. VB-FEM of RVE 2. (a) whole model; (b) matrix; (c) inclusions

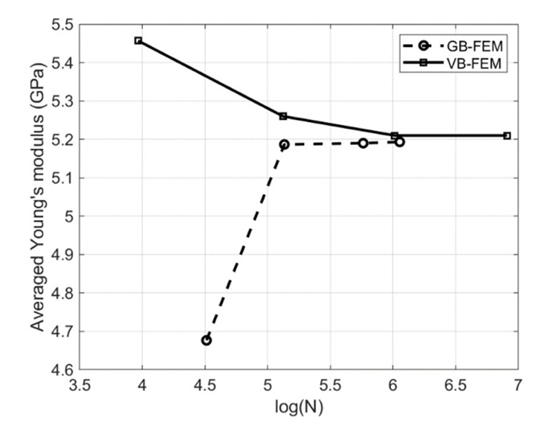Figure 10. Variation of RVE Young’s modulus with number of nodes (RVE 2)

The following observations can be made from the results:

1) With mesh resolution refined in VB-FEM, the normalized difference in volume fraction of inclusion, i.e. δ(V) in Table 2 and Table 3, is gradually reduced, indicating that VB-FEM and GB-FEM have closer volume fraction of inclusions, but it is difficult for them to have exactly the same.

2) VB-FEM and GB-FEM converge to very similar final solutions, which can be observed from the convergence curves in Figure 7 and Figure 10, and also from the normalized differences in Table 2 and Table 3. If the differences in the volume fraction of inclusions are taken in account, the solutions of VB-FEM and GB-FEM would be even closer.

3) Even with a coarse mesh resolution, VB-FEM solutions have good agreement with the converged GB-FEM. For example, with a 1:20 mesh resolution, the maximum normalized difference is only 1.10% for RVE 1 (Table 2) and 2.36% for RVE 2 (Table 3). Elimination of the differences in volume fraction of inclusions would further improve the agreement.

4) Regarding computational efficiency, GB-FEM has much greater advantage over VB-FEM for RVE 1, which can be seen from the convergence in Figure 7 and the normalized number of element nodes (η) in Table 2. However, for RVE 2, VB-FEM and GB-FEM have very similar efficiency, as shown by the convergence curve in Figure 10 and the η values in Table 3.

4. Discussion and Conclusions

The results of this comparison study show that for the elasticity prediction of particulate composites, GB-FEM and VB-FEM have similar accuracy upon their convergence. Regarding their computational efficiency, for a composite with large size and regularly distributed inclusions (e.g. RVE 1), GB-FEM has obvious advantage over VB-FEM; but for a composite with small size and randomly distributed inclusions (e.g. RVE 2), which is more often encountered in engineering, VB-FEM and GB-FEM have similar computational efficiency. Nevertheless, VB-FEM avoids all the difficulties of GB-FEM that have been discussed at the beginning of this paper. In addition, VB-FEM has a number of other advantages over GB-FEM. For the creation of VB-FEM, the only requirement is nonoverlap among inclusions, which is much easier to satisfy than the creation of a workable geometric model in GB-FEM. There is no restriction on how close two inclusions can be in VB-FEM; therefore, a high volume-fraction of inclusion can be achieved more easily. The accuracy and computational efficiency of VB-FEM are not affected by the number and the size of inclusions in the composite, as can be seen from the results of RVE 1 and RVE 2 obtained by VB-FEM. However, GB-FEM has to greatly increase the number of elements, because a large number of small-size elements are required to realistically represent the small inclusions and to fill in the very narrow gaps between infinitely close inclusions. If the volume fraction of inclusions is high, the situation will become even worse for GB- FEM [27].

Although GB-FEM and VB-FEM have similar accuracy in the prediction of composite elastic properties, there exist significant differences in the stresses and strains determined by the two models. Figure 11 (a) and (b) show the patterns of von-Mises (v-M) stress distribution produced by GB-FEM and VB-FEM for RVE 1 respectively. Quantitative differences can be observed from the results listed in Table 4.

Table 4. Maximum stresses and strains in composite matrix and inclusion (RVE 1)

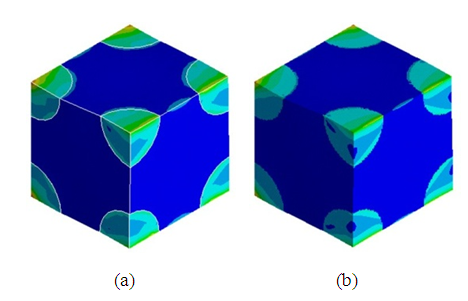Figure 11. Von-Mises stress distribution in RVE 1. (a) GB-FEM; (b) VB- FEM

The results in Table 4 show that, generally, with the mesh resolution refined, the maximum stresses and maximum strains predicted by VB-FEM gradually approach those by GB-FEM. However, even with a fine resolution such as 1:100, VB-FEM still overestimates the stresses and strains compared with GB-FEM. The main cause is that the interface between inclusion and matrix is not smooth in VB-FEM, which may cause stress concentration at the interface. It is well known that stresses and strains predicted by GB-FEM are also sensitive to mesh quality, especially in composites with irregularly distributed inclusions. As discussed before, distorted and degenerated geometric entities in GB-FEM produce distorted elements, which introduce spuriously large stresses and strains.

Based on this study, it can be concluded that VB-FEM can be used in replace of GB-FEM to predict elastic properties of particulate composites, but probably not suitable for predicting stresses and strains within the composites.

ACKNOWLEDGEMENTS

The reported research has been supported by Natural Sciences and Engineering Research Council (NSERC) of Canada in grant RGPIN-2019-05372, which is gratefully acknowledged.